灰色预测模型背景值的改进与应用

陈小彪 杨镇丞 柴立臣 连高社

(太原工业学院理学系 山西太原 030008)

灰色系统理论是一种介于白盒子和黑盒子模型之间的一种科学理论。它基于不完全、不准确、不确定的信息，使用数学方法和工程技术对系统进行分析、预测、控制和优化。与白盒子模型、即完全确定的模型不同，灰色系统理论的分析对象是那些难以用传统模型准确描述或缺少关键参数的系统。与黑盒子模型、即只考虑输入和输出之间的关系而不考虑内部结构的模型不同，灰色系统理论还考虑系统内部作用因素的影响。灰色系统理论在工业[1]、旅游、能源等预测问题中都有较好的应用。GM（1,1）是灰色系统理论中的一种重要预测模型，GM（1,1）预测适用范围广，且在预测时，只需要输入原始数据即可，不需要对数据进行平稳化、差分处理等操作，极大地方便了数据预处理过程，但GM（1,1）仍存在一些缺陷，影响了其实际应用，GM（1,1）模型的预测结果对初始值的影响较大，且GM（1,1）模型容易出现过拟合现象，在传统模型中，GM（1,1）模型对于背景值的计算采用的是相邻两数据的均值，但从面积角度来看，曲边梯形与直边梯形之间具有非常显著的差异，这就影响了模型的预测精度，所以，改进模型的背景值是减少模型预测误差的关键。

目前，许多学者对于GM（1,1）模型的背景值的算法进行了深入分析，旨在找到减少模型误差的有效方法，李凯[2]构造的背景值在一定程度上减少了相对误差，提高了代数精度。高宁[3]利用非齐次指数函数的方法来构造背景值，在一定程度上提高了模型的适用性。杨旭[4]基于灰色理论构造一种自适应的监测算法，在某种程度上增强了算法的适应性。李嘉诺[5]从背景值等权和不等权方面拓展了灰色GM（1,1）模型的使用范围。张丽洁[6]使用变权的方法优化了模型的背景值，效果较好。事实上，构造背景值的方法有多种，但都没有从根本上解决GM（1,1）模型的缺陷与不足，所以要更加深入地探究如何构造GM（1,1）的背景值，降低相对误差，提高代数精度和模型稳定性。

在传统的灰色预测模型中，背景值都是采用均值的方法去替代，但这种替代方式并没有结合点列的走向，均值替代并不能完全反映出点列的变化规律，影响到对点列的真实情况的判断。这是造成背景值产生误差的重要的原因之一，考虑到点列所构成曲线的走向，因此想到采用插值与机械求积来构造背景值。

1 传统的GM（1,1）灰色预测模型

2 模型背景值的优化

传统GM（1,1）模型的背景值是采用均值来进行计算，即

一般情况下，这样构造背景值会产生较大的误差。为提高精度，可以采用先构造插值函数，再对插值函数进行积分，用积分的值去取代梯形的面积，此类方法较原模型具有更高的精确度。

在现实应用场景中，所要预测问题的前提多为连续均匀变化的，所以采用等距的节的插值型求积公式。首先，要尽可能地提高代数精度，公式的阶数也不能取得过大，因为过大n会造成龙格现象，反而会对预测造成干扰，故选择柯特斯公式进行求积。

上述公式采用的是阶数n=4 时的牛顿柯特斯公式，提高了精度，同时也能较好地避免龙格现象，仍然保持该模型的适用性。采用柯特斯求积公式求背景值的方法如下。

为了更好地反映点列变化的趋势并且防止采取的点过多而产生过拟合现象，以k、k+1、k+2、k+3 这样的4个点作为插值节点，则可得到3次拉格朗日多项式Lk(t)为

将Lk(t)化简得

式（9）中，k=1,2,…,n-3。

当k=1，2，…，n-3，便可以解出z(1)(2)，z(1)(3)，…，z(1)(n-2)。对于剩下无法用公式计算的z(1)(n-1)、z(1)(n)，则采用传统方法进行计算。

综上所述以得到利用柯特斯公式和拉格朗日插值的方法构造的新的背景值公式z(1)(n-1)，z(1)(n)，最后可以简化得新的背景值构造公式为

3 数值实验

3.1稳定型数据序列

稳定型数据序列是指具有单调性的序列，该序列具有稳定的特征，且数据的完整性较高。采用稳定型数据序列可以较好地反映出该预测方法的有效性与稳定性。

表1 我国2011—2017年老年人口数的原始数据

为了验证权值分配的方法对稳定型数据序列的GM（1,1）模型的改进效果与稳定性，文章采用2011—2019 年的老年人口数进行预测，计算其相对误差，将各个方法的预测值与2018年、2019年的实际值进行比较，从而证明该方法可以有效提高精确度。

下面分别采用传统方法，李凯[2]构造的方法和文章的构造方法对2010—2017 年中国的老年人口数值进行拟合，得到2018年和2019年的预测值且与实际值进行比较。预测结果如表2所示。

表2 我国老年人口数的预测结果比较

通过比较和分析表2 的结果可以发现，改进的灰色模型具有更高的精度，2018年和2019年的相对误差率分别为1.76%、2.66%，相较于原模型和李凯等人的预测数据，误差明显降低，改进后的模型具有较高的预测精度，能够更好地反映数据序列未来的变化的趋势。

3.2缺失型数据序列

缺失型数据序列，指在原数据中出现了部分数据缺失现象的这一类数据。由于数据不是完整的，这就会导致预测的难度增加。对这类数据进行预测，可以检测预测模型对原始建模数据的恢复预测能力。

本文选择的是2012 届到2019 届的我国研究生报考总人数，在缺少2020 届的数据的情况下，预测2021届的研究生报考总人数。2012 届到2019 届的报考总人数如表3所示，预测结果如表4所示。

表3 我国2012—2019年考研人数的原始数据

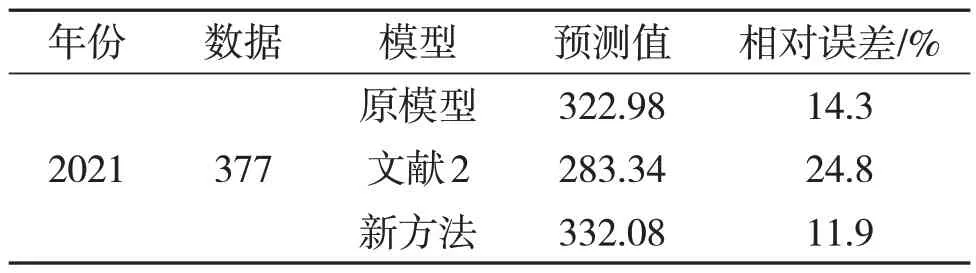
表4 我国考研人数的预测结果比较

通过比较可得，在缺少2020 届的数据下，该文改进的GM（1,1）模型相对误差仅为11.9%低于原模型，文献[2]的相对误差，说明了即使在缺失型数据序列的下，改进的GM（1,1）模型也能够起到较好的预测效果。

4 结语

在传统的GM（1,1）预测模型中，其误差主要来自背景值的取值。但现在对背景值的构造大多只是简单地采用梯形公式与辛普森公式，所以造成其代数精度不够高，或又是构造插值函数选取的点列过多，造成过度拟合。文章基于柯特斯公式和拉格朗日插值构建出新的GM（1,1）模型的背景值，并将模型应用于我国老年人口数量的预测，经过对比可以看出，改进的GM（1,1）模型具有较高的精确度，且具有较好的预测稳定性。