基于HPM的高中数学概念课教学设计与应用研究*
——以“函数的概念”教学为例
2023-08-04江苏省仪征中学邓迎春
江苏省仪征中学 邓迎春
南京师范大学第二附属高级中学 张晓飞
《普通高中数学课程标准(2017年版2020年修订)》(后面简称“课标”)指出:函数是现代数学最基本的概念,是描述客观世界中变量关系和规律的最为基本的数学语言和工具,在解决实际问题中发挥重要作用.函数概念是高中数学很重要的基础概念之一,但是很多学生忽视对函数概念的理解.不少学生存在这些疑问:“为什么初中已经学习了函数的概念,高中还要学习新的概念?是不是到了大学还要学习函数新的定义?函数的概念到底是怎么产生、怎么发展的?”
在数学教学中一定要突出数学本质,而这就需要在教学过程中让学生深入理解数学概念,理解数学本原性知识,了解数学历史、数学文化,掌握数学思想,体会数学思维方式,并学会对数学美的鉴赏.很多研究已表明,将数学史融入教学有助于学生认识数学发展规律和数学本质,只有让学生经历了知识的产生、发展过程,才能将数学冰冷的美丽转变为火热的思考.鉴于此,在2020年秋季学期本校骨干教师教学展示活动中,笔者就“函数的概念”这一课题,尝试从HPM的角度进行教学设计,通过若干情境,结合数学史对函数概念的教学进行了重构,加强函数概念发展史内容的渗透,促使学生更好地掌握本节课内容,提升学生的人文情怀,提高学生的数学核心素养.现整理成文,与各位同仁共勉.
1 教学设计与实施
1.1问题情境与学生活动
托马斯曾说过:“函数概念是近代数学思想之花.”今天老师和大家一起学习“近代数学思想之花”——函数的概念.可能同学们会有疑惑,初中已经学过函数的概念了,为什么到了高中还要学习?难道函数还有不同的定义?其实函数的概念经历了几次抽象的过程,下面我们就以教材中的三个现实生活问题为载体再重温一下函数概念的发展历史.
情境1某城市在某一天24 h内的气温变化情况如图1所示,试根据图象回答下列问题:
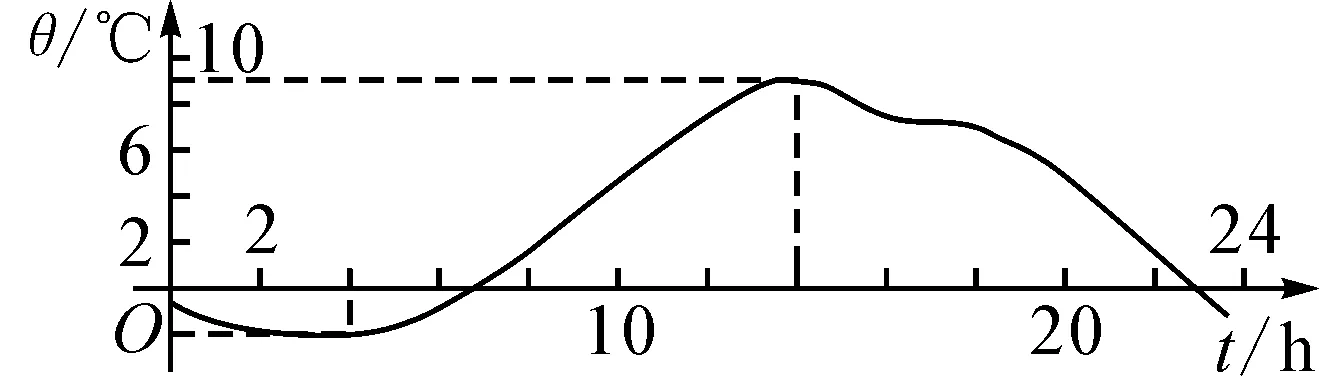
图1
(1)这一变化过程中,有哪几个变量?
(2)如果一个动点P在这个曲线上运动,它的横坐标、纵坐标有关系吗?
情境说明:此情境中有时间和温度两个变量.如果动点在曲线上运动,动点P的横坐标、纵坐标是相互依赖的.其实在历史上,法国数学家笛卡儿在《几何学》一文中首先引入变量思想,将变量称为“未知和未定的量”.1673年,牛顿在微积分的讨论中,使用“流量”来表示变量间的关系.同年,莱布尼茨创造了函数function一词,表示任何一个随着曲线上的点变动而变动的量的纵坐标.此时为函数概念的萌芽时期.
情境2一物体从静止开始自由下落,下落的距离y(单位:m)与下落的时间t(单位:s)之间满足什么关系?
(1)上述情境中,有几个量?常量是哪些?变量又是哪些?
(2)可以通过什么来刻画两个变量之间的关系?
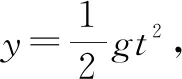
情境3估计人口数量变化趋势是我们制定一系列相关政策的依据.表1是我国从1949年至1994年人口数据资料:
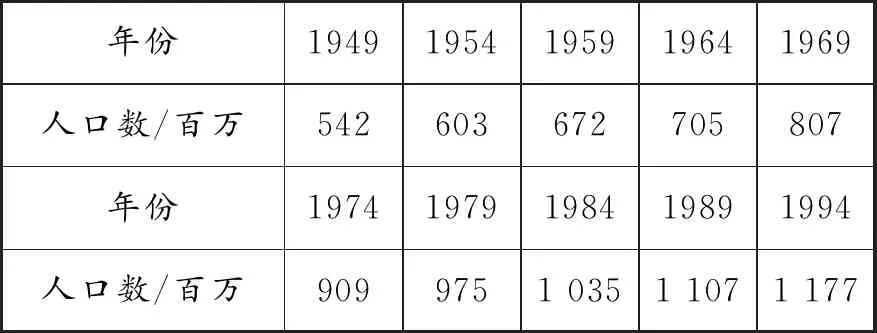
表1
(1)表1中有变量吗?有几个变量?
(2)当年份确定后,当年的人口数是否确定?你能写出人口数关于年份的关系式吗?
情境说明:“是不是所有的变量都能用解析式表示?”在18世纪中期,随着生活和科技的发展,出现了这样的新问题.如表1中的变量为年份和人口数,当年份确定时,对应年份的人口数也是确定的,但是我们无法写出人口数关于年份的关系式.18世纪20年代,德国数学家狄利克雷给出如下函数定义:对于在某区间上的每一个确定的x的值,y都有一个确定的值,那么y叫做x的函数.这时,我们才认为函数概念的本质已经形成,即数学人常说的函数的经典定义,也称“对应定义”.
思考1:结合上述三个情境问题,如何用集合语言描述两个变量?
思考2:如何用集合语言描述函数的变量对应关系?
思考3:基于以上两点思考,你能尝试用集合的语言给出函数的定义吗?
在1930年,近代函数的定义为:若对集合M的任一元素x,总有集合N中唯一确定元素y与之对应,则称集合M上定义一个函数,记为y=f(x).元素x称为自变元,元素y称为因变元.
历经数百年,函数概念经过好几代数学家的锤炼、革新,至此,数学家们完成了近代函数概念建构的全过程.但这并不一定是函数概念的终结版,随着科学的发展,函数的概念还在继续发展.
1.2意义建构和数学理论
苏教版必修1(2020年7月第一版)给出的函数定义如下:
一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有唯一的实数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function),记作y=f(x),x∈A.其中,x叫作自变量,集合A叫做函数y=f(x)的定义域(domain).
思考4:高中的函数定义与近代函数的定义有没有区别?
思考5:初中的函数定义与高中的函数定义有什么异同?
思考6:高中函数定义的基本要素是什么?
近代函数定义建立在集合上,高中函数定义建立在非空实数集合上;高中的定义是从集合、对应的观点出发,而初中给出的定义是从运动变化的观点出发,本质是一样的,都是一种对应关系,不同的是叙述的方式.此三个思考,能更好地帮助学生在已有的知识基础上理解新的知识,并融会贯通.
1.3数学运用
例1判断下列对应是否为函数,如果是函数,你能否说出其定义域和值域?

例2判断下列各组函数是否为同一函数?
设计意图:例1是训练学生用概念来解析问题,加强对函数本质的理解.通过例1强调函数概念中的“任意性”与“唯一性”,并促使学生关注到,对应的是结果,而不是过程.例2是概念的再理解应用,函数的定义域相同,且相同的变量值对应的函数值也相同,那么这两个函数就是同一函数.简单地说,如果两个函数的三要素(定义域,对应关系,值域)相同,那么这两个函数就是同一函数;更简单地说,定义域和对应关系相同的两个函数即为同一函数.函数的表达与字母的使用无关.
1.4总结与反思
问题:同学们,今天我们一起徜徉在历史长河中,经历了函数概念的萌芽、发展到逐步完善的过程,并学习教材中函数的定义,你有什么收获?
设计意图:总结和反思可以帮助学生厘清这节课的“为何”和“如何”的问题,即为何要学习本节课的知识,又是如何学习的,并形成知识体系,提升学科素养,使学生更深层次地理解三百多年来函数概念的发展与生产、生活以及科学技术的实际需求紧密相关.
有的学生认为函数概念的发生、发展都离不开生活,生活是科学发展的原动力;有的学生总结说了解到函数概念一步一步逐渐发展成熟的过程,知道了函数概念的来龙去脉,理解了概念的本质;还有的学生觉得人们认识函数概念的过程是非常曲折的,科学研究需要不断的学习与创新;等等.
1.5课外自主探索
自主搜索“狄利克雷函数”,并了解它在函数概念发展中的作用.
设计意图:从课内到课外,使学生能主动地有意识地参与到数学史和数学文化的学习中,认识到数学史和数学文化在数学学习中的作用和意义,并能借助课堂上学习的思想和方法,形成自主学习新知识的意识和能力.
2 教学反思与感悟
HPM是一个富有魅力、前景广阔、特色鲜明的学术领域.它既需要有一定的数学和数学史功底,也需要掌握数学教育的理论与研究方法;既需要有坐“冷板凳”的功夫,也需要有较强的社会实践能力.
2.1 以史为鉴,激发学生数学学习热情
本节课的授课对象为江苏某四星级高中高一普通班学生.从教学过程看,学生课堂回答问题的主动性、积极性很高.学生对函数概念的“前世今生”也非常感兴趣,在学习过程中,学生时而穿越时空,与先哲对话,汲取思想养料,探索教学方法;时而回归现实,走入心灵之中,探索数学学习的历史相似性;教师也时而掩卷深思,品味成败得失,展望数学教育美好的明天.在课后与同学的交流中,大部分学生赞同课堂中适当融入数学史,以激发学习兴趣,也有利于培养高中生数学抽象和逻辑推理核心素养.
2.2以史启真,培养学生正确的数学观
函数概念是高中数学中很重要的知识点,但是学生学习之初会感到很困惑:初中已经学习过函数的概念,为什么又要学习函数的另外一种概念?同时,学生对函数概念的理解往往局限于一次函数、二次函数等特殊的简单函数,对函数概念存在不少片面认识.本节课通过对函数概念发展历史的简单重构,引领学生经历了函数概念发展的四个时期,了解了数学概念发生、发展的曲折过程,明确了科学知识发生、发展的源动力.法国大数学家庞加莱也说:“如果我们想预见数学的未来,适当的途径就是研究这门学科的历史和现状.”基于HPM重构高中数学课堂,避免了简单地告知知识点是什么,怎么答题,而是把数学的本质展现出来,通过系列本源性问题,促进学生的思考和探究,最终实现培养学生数学核心素养的目标.
2.3以史促思,培养学生的数学思维
我们要知其然,还要知其所以然.“为什么会萌发函数概念?为什么要明确函数概念?为什么要完善函数概念?”这些都是数学本原性问题.用好数学史,可以帮助学生回归、溯源、思考原始问题,启迪学生思维.大力挖掘数学史的教育价值,将这些方面用到日常数学教学中,对于增进学生的数学问题意识,培养学生数学思考的习惯和独立钻研的能力,启发学生的思维和方法,提高数学的创新水平等都具有重要的作用.纸上得来终觉浅,绝知此事要躬行,要使学生从被动的学习到主动地探究,从知之到乐之.
