落石冲击作用下X80架空管道力学响应分析
2023-08-03程丽璇周泽山刘建勋文星强王晓黎
程丽璇,周泽山,刘建勋,文星强,杨 颖,尹 浩,王晓黎
(1.中国石油西南油气田公司储气库管理处,重庆 401121;2.重庆科技学院石油与天然气工程学院,重庆 401331;3.重庆科技学院机械与动力工程学院,重庆 401331;4.大庆油田工程有限公司,黑龙江 大庆 163712)
1 引言
目前在我国长距离输油气管道中,沟壑、山涧等许多危岩体地段采取架空管道进行铺设。而坍塌、山体滑坡、爆破和施工等产生的落石容易对管道(特别是架空管道)造成危害,极易使管道失效[1]。例如重庆忠县路发生了岩石坠落后发生管道冲击变形事故[2]。汶川地震发生后,兰成渝管道由于落石撞击造成原油泄漏,澜沧江跨越管道同样遭到落石威胁[3]。崩塌落石是造成管道失效迫害的主要原因之一。其中,X80钢管道具有抗大变形的特点,在长输油气管道建设中应用广泛。因此研究X80钢管道在地质灾害作用下力学响应规律有重要意义[4]。
对于崩塌落石对管道的危害性,国内外已有许多研究,特别是近年来崩塌落石危害性受到越来越多的关注[5]。Rao等[6]采用两阶段法,分析了落石冲击对管道的变形情况,基于Pasternak地基模型和Winker地基模型分别计算落石冲击荷载对管道变形的影响。荆宏远[7]采用ANSYS/LS-DYNA分别从理论计算和数值仿真两方面研究在落石冲击中心点处,截面的变形规律,由圆形变为长轴为水平向的不规则椭圆形,最大有效应力出现在管道顶部。上官方媛等[8]运用RockFall软件建立模型,探究不同质量落石撞击管道时,落石的最大动能等特性参数影响规律。邢义锋等[9]利用有限元软件ANSYS/LS-DYNA,考虑了管道内压、落石水平距离等影响因素对落石冲击过程进行了数值模拟分析,研究管道应力变化规律。张杰等[10]对地面架设油气管道过程进行数值模拟,研究冲击速度、落石冲击位置等对管道冲击变形的影响规律。王等等等[11]采用CAESARⅡ软件建立了架空及埋地管道系统的模型,根据分析2种情况下管道一次应力、二次应力出现的位置,得到架空及埋地管道敷设设计经验。吴世娟[12]将数值模拟软件RockFall和CAESARII相结合,分析了落石质量和下落高度对落石运动过程的影响,得到落石撞击管道时落石携带最大动能的影响规律。
综上所述,现对于落石冲击埋地管道研究较多,而关于多种落石形状冲击架空管道的文献较少,因此本文采用ABAQUS有限元软件对4种落石冲击架空管道工程进行数值模拟,进一步分析落石形状、落石速度、管道壁厚、管道内压等敏感性因素对冲击管道的力学响应规律,为管道敷设、管道防护以及安全评价提供借鉴。
2 有限元模型建立
在ABAQUS/Explicit模块下建立X80钢管道模型,模拟不同落石冲击架空管道动力响应过程,管道建模采用壳单元,单元类型为S4R四节点缩减积分。4种落石(球体、正方体、楔形纵切、楔形拐切)的建模均采取均质实体,单元类型C3D8R为线性显示三维应力单元[13],管道材料定义为双线性各项同性材料。管道长度4 m[14],管道外径0.693 m,管壁厚度0.023 m。球形落石的半径为0.31 m,正方体落石的边长为0.5 m,4种形状落石的质量均为250 kg。落石均设置为刚体,4种落石下落的方向沿管道中心与轴线方向垂直。所选材料参数[15],见表1。

表1 材料参数与所选单元类型
为更好地观察落石冲击管道中间接触区域的应力应变情况,提高数据精度,对落石冲击管道中间接触区域进行网格加密,网格由中间向两端逐渐稀疏[16],管道网格共划分8 900个,球体落石网格共划分7 168个,正方体落石网格共划分2 197个,楔形纵切、楔形拐切落石网格共划分1 700个。有限元模型图如图1所示。管道两端采用约束的方式设置为完全固定。释放落石在接触方向的位移,其余方向均为零。

图1 径向冲击管道有限元模型
3 评价准则
目前,国内外学者对落石运动的预测方法主要有经验分析、理论公式计算及数值计算方法等[17]。在实际工程中,X80管道为弹塑性体,一旦遭受落石冲击,管道大部分会达到屈服强度。因此,分析管道是否失效大都根据应力和应变的方法来判断。
3.1 等效应力
模拟研究的管道为X80钢,由于管道在运行过程中受到环向应力、轴向应力和径向应力,即三向应力状态,因此,在这种复杂条件下,使用Von Mises屈服准则,即当等效应力超过材料的屈服应力时,就会发生屈服,将会产生塑性变形。研究将采用第四强度理论计算管道受到撞击后的等效应力,屈服失效的条件可用下式来表达[18]:
式中,σMises为Von Mises屈服条件下的组合应力;σ1、σ2、σ3分别表示第一主应力、第二主应力和第三主应力;φ1表示设计系数。
3.2 管道应变
管道受到外荷载冲击后会产生变形,变形量过大将导致管道破坏失效。管道应变分为压缩应变、拉伸应变和椭圆化变形。当管道受到落石撞击后,其应变应满足下列要求[19]。
管道压缩应变的相关要求:
管道拉伸应变的相关要求:
管道椭圆化变形的相关要求[20]:
式中,σcf为压缩应变的阻力因子;σct为拉伸应变的阻力因子;Dmax为最大管外径;Dmin为最小管外径。
4 落石冲击下管道力学响应特征分析
图2为落石以10 m/s的速度冲击管道时管道的应力应变变化过程。由图2(a)、2(d)可见,球形落石和楔形拐切落石冲击下管道力学响应特征基本一致,大致分为3个阶段,具体为:阶段1,落石与管壁已接触,接触为单点接触形式,落石冲击力传递至管道顶部;阶段2,冲击应力迅速增大,管壁发生较大变形,接触点沿径向向内凹陷,应力波向接触点周界范围同步传播;阶段3,此时落石与管壁接触后发生一定程度上的回弹,管壁变形减小。相比较球形落石,楔形拐切落石冲击下管道冲击变形较大。

图2 4种落石冲击过程管道应力云图(俯视图扩大3倍,侧视图扩大2倍)
由图2(b)、2(c)可见,正方体落石和楔形纵切落石冲击管道过程相似,也可分为3个阶段,具体为:阶段1,落石与管壁已接触,应力和变形逐渐增大,在阶段2时,随着进一步接触,管壁应力急剧上升并发生较大变形,阶段3时,落石与管壁接触后发生一定程度上的回弹,管壁应力下降且变形减小。不同之处在于,楔形纵切落石冲击管道线接触较明显,变形为线形凹陷。通过分析比较4种落石冲击管道的凹陷深度以及Von Misis应力,4种落石最大Von Mises应力均达到了屈服强度572 MPa,表明在当前分析条件下,管道产生塑性变形且楔形拐切冲击时对管道伤害较大。
图3为4种落石撞击管道时的能量变化图。为便于描述,将冲击过程划分为冲击前、冲击中和冲击后3个过程进行,由四幅能量时程响应曲线图可以看到,动能减小的同时,管道内能(应变能和耗散能)增加,管道变形能上升到峰值后随着变形的恢复而下降,耗散能随着管道的永久变形一直上升后持平。当落石的速度降至零时,落石的重力势能全部转化为内能,其撞击动能被管道完全吸收。在冲击过程完成后,落石开始反弹,而在落石反弹过程中,其冲击力逐渐减小,管道能量完全释放出来,此时,能量变化和撞击前的能量变化相反。由于管道为弹塑性体,所以管道吸收的能量不能全部转化为落石的动能。耗散能冲击过程中一直存在,因此每个落石的动能始终不能恢复到管道最初的动能。

图3 4种落石冲击管道能量时程响应曲线
图4给出了不同形状落石作用下撞击区域中心点处的管道应力时程响应曲线。可以看出,不同形状落石冲击后对管道的应力变化值由大到小依次为:楔形拐切、球形、楔形纵切、正方体。其中这4种情形下管道应力波动过程中整体都呈现先上升后下降的趋势。在当前分析条件下,楔形拐切对管道的危害最大,正方体落石对管道的伤害最小。
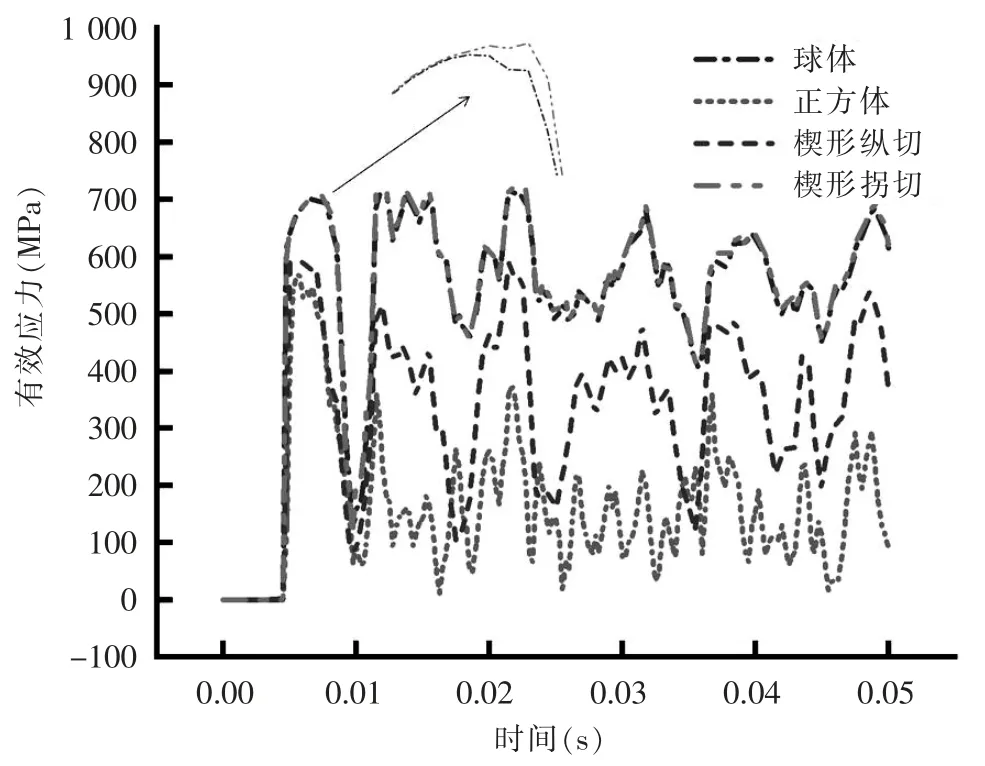
图4 4种形状落石撞击下管道的应力变化
5 敏感性因素分析
落石冲击管道是一个常见而又复杂的动态过程,冲击和研究过程较复杂,不同因素对管道的影响也不一样。因此,采用控制变量法,假定一些因素不变时研究某一因素变化对管道的影响。对实际工程常见的几种影响因素,如管道壁厚、管道内压、冲击速度等4个影响因素进行管道力学响应分析。
5.1 冲击速度影响分析
图5为不同冲击速度下管道的最大冲击坑深。由图可知,冲击速度越小,冲击管道坑深就越浅,数值曲线越接近。速度一定时,坑深由大到小依次为楔形拐切、球形、楔形纵切、正方体。随着冲击速度的增大,四种冲击坑深均逐渐增大。例如,当冲击速度由6 m/s增大至14 m/s时(冲击速度增加2.33倍),4种冲击坑深分别增大至32.13 mm、30.38 mm、21.7 mm、18.4 mm,坑深增加3~4倍。
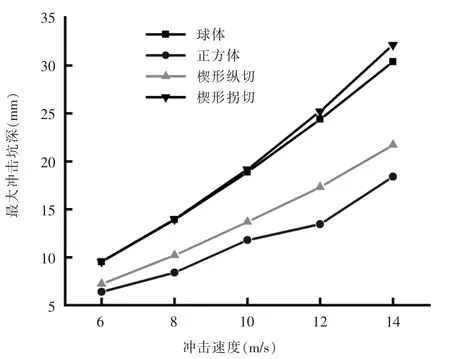
图5 落石冲击速度对冲击坑深的影响
由图6可知,当球形落石冲击管道时,高应力区出现在管道上方冲击位置处,冲击速度越大时,管道受力越大。以上分析规律表明,在当前分析条件下,拐切落石冲击管道时冲击速度对坑深更为敏感。

图6 落石冲击速度对冲击Von Mises应力的影响(球形)
5.2 管道内压影响分析
长输管道内压对落石冲击有减缓作用。图7所示4种落石冲击不同内压管道后的最大冲击坑深。压力管道的冲击坑深的变化随着内压的增大而降低,呈非线性规律变化。这是因为管道内压的增加提高了管道的抗变形刚度。以球体落石为例,当管道内压为4 MPa时,最大冲击坑深约为17.7 mm;管道内压为12 Mpa时,最大冲击坑深为15.2 mm。整体而言,当管道内压由4 MPa增大至12 Mpa时(管道内压增加3倍),坑深减小0.1~0.3倍。

图7 管道内压对冲击坑深的影响
由图8可知,当球形落石冲击管道时,随着内压增大,管道Von Miss也逐渐增大,因此,应当采取保护措施降低管道应力,使其位于屈服极限范围内。可见,在铺设管道和研究压力管道的冲击问题时管道内压的影响不可忽视。

图8 不同管道内压对冲击Von Mises应力的影响(球形)
5.3 管道壁厚影响分析
由k=πE(D4-d4)/64可知,管道壁厚影响其刚度。当落石冲击速度为10 m/s时,4种落石冲击不同壁厚管道后的最大冲击坑深及Von Mises应力如图9、图10所示。由图可知,管道壁厚越小,管道最大冲击坑深越大,管道的屈曲现象更为严重。以球体落石为例,当管道壁厚为14mm时,最大冲击坑深约为42.8mm;管道壁厚为26 mm时,最大冲击坑深为15.7 mm。整体而言,当管道壁厚由14 mm增大至26 mm时(管道壁厚增加约2倍),4种落石冲击坑深分别增大至15.7 mm、15.6 mm、11.1 mm、9.8 mm,坑深减小2-3倍。由图10可知,随着管道壁厚的增大,管道高应力区出现在管道顶部,管道顶部Von Mises应力也随着壁厚的增加逐渐减小,且管道均达到屈服极限后产生塑性变形。故管道壁厚较小时,应对管道采取防护措施。相同情况下,管道壁厚越大,管道的破坏失效风险越小,这是由于管壁越厚,其抵抗外力作用变形的能力越强,所以能承受的外力越大。因此,在实际工程中,薄壁管道在落石冲击作用下更容易失效,应尽量采用管壁较厚的管道。
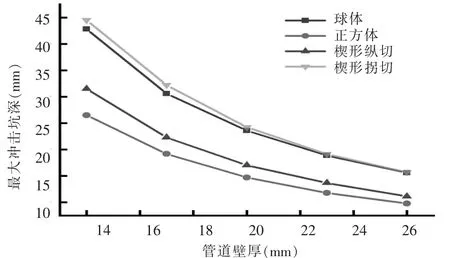
图9 管道壁厚对冲击坑深的影响

图10 不同管道壁厚对冲击Von Mises应力的影响(球形)
6 结论
针对落石冲击架空管道的问题,建立了4种落石(球体、正方体、楔形纵切、楔形拐切)冲击管道的有限元计算模型,对落石冲击管道力学行为进行模拟分析,研究了4种落石冲击过程以及冲击速度、管道内压、管道壁厚等因素对管道的应力和变形的影响,得出以下结论:
(1)4种落石冲击管道过程中,由于产生耗散能,因而四种落石冲击后的能量值不能恢复到冲击之前。冲击过程降低落石速度,在冲击模拟过程中,管道的应力达到屈服强度,对管道产生塑性变形。应采取防护网等措施降低落石冲击速度。
(2)随着落石冲击速度的增加,管道的最大坑深(凹陷程度)也逐渐增大;管道的内压和壁厚越大,受冲击后,管道的最大坑深(凹陷程度)逐渐减小。高应力区出现在管道顶部,应对管道顶部采取保护措施。
(3)通过对四种落石冲击管道过程的模拟可知,不同形状落石对管道的伤害程度不同。其中,楔形拐切落石冲击时对管道伤害较大,正方体落石最小。因此,建议对崩塌易发、多发区域,增强管道沿线排查力度,采取措施对楔形等不规则危岩体进行排险。
