基于集成学习的土壤含水量预测研究——以辽西地区为例①

付平凡，杨晓静*，苏志诚，屈艳萍，马苗苗

基于集成学习的土壤含水量预测研究——以辽西地区为例①

付平凡1,2，杨晓静1,2*，苏志诚1,2，屈艳萍1,2，马苗苗1,2

(1 中国水利水电科学研究院，北京 100038；2 水利部防洪抗旱减灾工程技术研究中心，北京 100038)

准确高效地预测土壤含水量(SMC)对田间水分管理至关重要。本研究利用在辽西地区自建的3个站点2018—2021年10 ～ 40 cm土壤水分自动观测小时数据集，分析研究随机森林(random forest，RF)和梯度提升机(gradient boosting machine，GBM)算法在SMC预测方面的适用性，验证不同时间尺度SMC的预测结果。同时引入SHAP(shapley additive explanations)方法表征5类(降水、日照时数、平均相对湿度、风速、平均气温)输入变量对SMC预测结果的影响，并制定区间划分规则识别变量最大贡献阈值区间。研究结果表明：年尺度下，SMC 预测GBM模型和RF模型2分别为0.982和0.888，气温贡献最大，最大贡献区间是21 ～ 23℃；季尺度下，2种模型2分别为0.935和0.863，日照时数贡献最大，最大贡献区间为2 ～ 4 h。该研究创新应用SHAP方法于机器学习输入变量贡献度分析，同时验证了2种机器学习算法对SMC预测研究的准确性，可为SMC相关研究提供参考。

集成学习；土壤含水量预测；梯度提升机；随机森林；辽宁西部；SHAP值

土壤水分是区域水循环、农业灌溉管理和气候变化的特征要素之一，其在水文、气象、农业等学科中也具有重要的作用[1]。土壤含水量(soil moisture content，SMC)是地表植被吸收水分的主要来源，其对作物的生长发育至关重要[2]。因此，准确预测土壤含水量对作物增产和粮食安全具有重要意义。

目前主要的土壤水分预测方法有经验模型法[3]、土壤水动力学法[4]、时间序列模型法[5]以及机器学习算法[6]等。近年来，随着计算机技术的快速发展，机器学习算法已成为一种重要的预测土壤含水量的手段[7]。集成学习(ensemble learning)是通过构建并结合多个机器学习器来完成任务，具有较强的泛化能力[8]。由于集成学习模型相比传统机器学习模型在性能上表现更为出色，目前集成学习中的随机森林(random forest，RF)和梯度提升机(gradient boosting machine，GBM)模型已在农业干旱监测、骤发性干旱研究等领域有所应用[9-10]。Cai等[11]结合GBM与RF模型系统论证了这两种方法预测净生态系统碳交换的有效性；Prodhan等[12]也将RF和GBM进行非线性集成，利用ISI-MP作物模型定量分析了未来干旱对作物产量的影响。以上研究都表明，RF和GBM模型具有较好的实用性，但此类方法在土壤含水量预测的适用性研究上亟待进一步深入。

由于机器学习模型是黑箱模型，现有的多数研究主要基于评估指标来对模型的结果进行评价，而针对输入变量对预测结果影响的研究还相对较少。为解决这一问题，Lundberg和Lee[13]在2017年提出了SHAP(shapley additive explanations)方法，该方法基于合作博弈理论定量化表征每个特征对最终预测值的影响，增加了模型的可解释性。近年来，已有研究利用SHAP方法解释机器学习模型，王鑫等[14]融合LightGBM模型与SHAP方法分析得出了血清胰岛素、葡萄糖浓度和年龄是患者是否患有糖尿病的关键因素；Kannangara等[15]利用RF模型和SHAP方法，分析了9个输入变量对隧道开挖引起沉降的影响，结果表明土壤类型的影响最大。目前SHAP方法已应用于金融欺诈、污水处理、电力系统紧急控制等领域输入变量对预测结果的贡献研究[16-18]，但在土壤水分预测方面上的应用还相对较少。因此，将SHAP方法应用于土壤含水量预测研究，可定量识别输入变量对土壤含水量的贡献程度，为缺省输入因子情况下的变量选择提供依据。

本文拟将集成学习中的RF、GBM算法应用到土壤含水量预测研究，拓展验证2种算法在土壤含水量模拟预测中的适用性；且为解释各变量对于预测模型的影响，引入SHAP方法定量评估集成学习模型输入变量的贡献程度，并基于制定的区间划分规则识别特征敏感阈值区间，为解释输入变量对预测值的影响和土壤含水量预测方法的选择提供新的参考。

1 数据与方法

1.1 研究区概况

研究区为辽西地区(119.70° E ～ 122.53° E，40.35° N ～ 42.24° N)，包括阜新、朝阳、葫芦岛和锦州4市，属于温带大陆性季风气候，多年平均降水量约为450 ～ 700 mm，其中夏季降水量约占全年降水量的2/3。全年四季分明，雨热同期，日照丰富，年均温7.2 ～ 8.3℃。根据2021年辽宁省统计年鉴的结果，辽西地区主要的粮食作物为玉米，占全省粮食作物种植面积的41.2%。区域内含辽西走廊和辽西北部低山丘陵2个区域，地势呈现西北高、东南低的空间分布态势[19]。研究所选墒情站点均位于玉米种植区，其空间分布如图1所示。凌海站位于低山丘陵区的凌海市东部，土壤类型为棕壤；孙家湾站位于朝阳市东北部大凌河干流附近，地形为黄土丘陵，土壤类型为褐黄土；叶柏寿站位于朝阳市建平县南部，地形为丘陵坡地，土壤类型为褐黄土。

1.2 数据来源与质量控制

1.2.1 数据来源 研究应用的数据主要包括小时土壤含水量数据集和气象要素数据集。

1)小时土壤含水量数据集来源。2018年7月在辽西地区选址(大凌河出口的凌海站，干流中部附近的孙家湾站，支流的叶柏寿站)并安装3套土壤墒情自动监测系统。该系统所使用的土壤水分传感器长期埋设在野外大田的测点中，并基于时域反射原理(time domain reflectometry，TDR)对不同深度土壤进行土壤体积含水量测定。站点的数据时间序列始于2018年7月，10 ～ 40 cm深度传感器实时接收间隔为1 h的土壤墒情数据。为验证数据的有效性，分季节进行7次人工取土实验，利用烘干法将测定的土壤含水量与自动监测站监测结果进行对比，对比结果表明各深度土壤含水量同步监测差值小于10%。

2)气象要素数据集来源。由于墒情站点的数据序列起始时间为2018年7月，为匹配对应日期的墒情数据，选择2018—2021年气象数据作为模型输入变量，气象数据来源于中国气象数据网(http://data. cma.cn/)。3个气象站点气象要素包括逐日的降水、日照时数、平均相对湿度、风速、平均气温。

1.2.2 数据质量控制 为降低异常数据对模型预测结果准确性的扰动，从两个方面对数据进行质量控制。

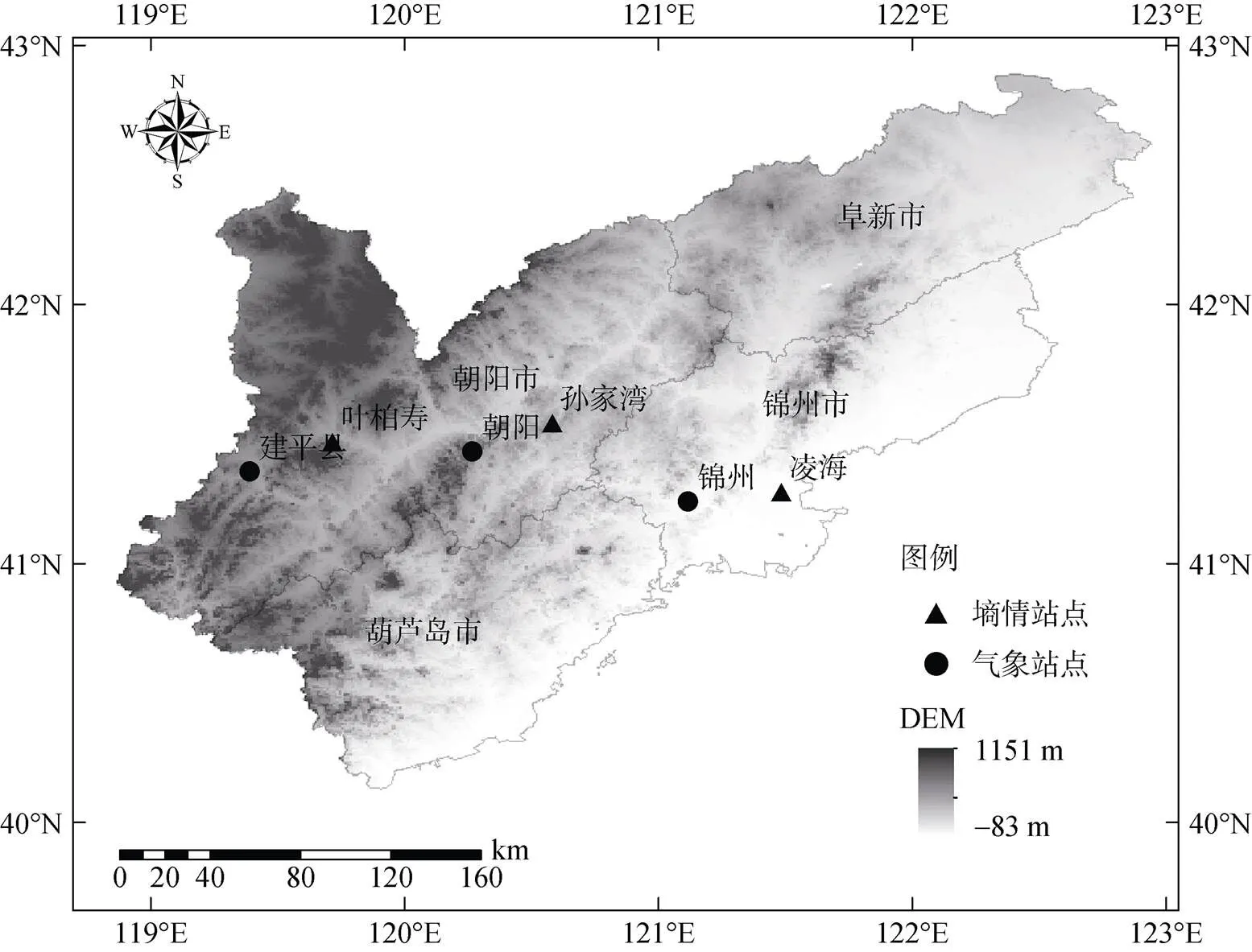
图1 研究区和3个试验站点示意图

1)数据有效性控制。为保证数据集的有效性，将墒情站和气象站空值数据剔除后，孙家湾站共有数据1 099条，叶柏寿站共有数据1 202条，凌海站共有数据1 177条。

2)数据量纲控制。为避免不同输入变量之间数量级别和量纲的影响，将输入和输出数据进行归一化处理，计算公式如下：

式中：x为归一化后的样本集；为原始样本集；min为原始样本集最小值，max为原始样本集最大值。将每日8:00的土壤墒情数据作为当日值，并按照8︰2的分配原则进行训练集和测试集的划分。

1.3 研究方法

1.3.1 集成学习 集成学习是一种融合多个机器学习模型的集成模型，通过某种融合策略常可获得比单一模型显著优越的泛化性能。集成学习不仅能够实现模型之间的优势互补，还能减少对训练所需数据的依赖程度[20]。常用的融合策略有3种：Bagging、Boosting和Stacking。本研究采用Bagging中的RF、Boosting中的梯度提升决策树(GBDT)算法，所使用的2种方法的建模过程均在Python语言环境下加载scikit-learn实现。

梯度提升机(gradient boosting machine，GBM)是由Friedman[21]提出的一种流行机器学习的集成方法。为了解决回归和分类问题，GBM通常是以决策树弱模型组合的形式，周期性地构造出一个鲁棒模型。Gradient Boosting与一般的Boosting算法一样，也是一个迭代的过程，Gradient Boosting每个新的模型是沿着前面模型的残差减少的梯度方向上建立，每次的训练是为了改进上一次的回归结果。为了减少模型的残差(residual)，通常采用牛顿–拉弗森方法(Newton- Raphson method)在残差减少的梯度(Gradient)方向拟合一个新的模型[22]。由GBM构建的梯度提升回归模型有5个需要优化的参数，分别为学习率(learning_rate)、损失函数(loss)、决策树的数量(n_estimators)、决策树的深度(max_depth)和建立决策树时选择的最大特征数目(max_features)。利用GridSearchCV方法[23]进行超参数随机匹配择优，经过调参后，n_estimators=300，max_depth=10，max_features=2，loss='huber'函数，learning_rate=0.1为最优参数。

随机森林(random forest，RF)算法是一种通过集成大量的决策树来改进分类和回归的方法。Breiman[24]引入的RF是一种基于bootstrap聚合的决策树集合，通过随机选取广泛应用于回归问题的预测器子集，计算预测变量并基于预测变量的数据分割，得到因变量的均方根误差(RMSE)最佳估计。在RF回归中，引入的RF算法将自动创建随机决策树群，通过从训练数据集中选择随机变量集，并采用随机有放回抽样的方法来构建每棵树，最后通过对所有树的均衡化结果来计算观测值的预测值。RF模型有3个需要优化的参数：决策树的数量(n_estimators)、决策树的深度(max_depth)和建立决策树时选择的最大特征数目(max_features)。利用GridSearchCV方法进行超参数随机匹配择优，经过调参后，n_estimators= 900，max_depth=15，max_features=5是最优参数。

1.3.2 模型评价指标 选用平均绝对误差(MAE)、决定系数(2)[25]和均方根误差(RMSE)3种指标分别对GBM、RF预测模型进行预测效果评估。评价指标计算公式如下：

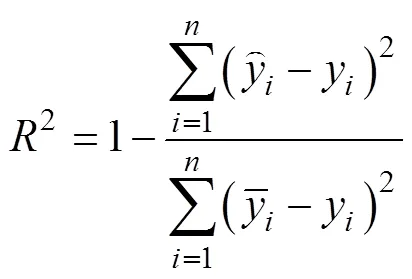
1.3.3 SHAP方法 SHAP方法是一种直观的、合理的解释模型的方法，该方法通过计算每个特征对预测值的贡献来解释特征，所使用的值(SHAP值)可定量化表征各个特征对预测值的贡献，SHAP值越大表明该特征对于预测值的贡献越大。SHAP方法是以合作博弈理论为基础计算SHAP值，特征值的SHAP值是对所有可能的特征值组合进行加权求和，其公式如下：

式中：是模型中使用的特征的子集，表示这些特征不包括在集合中；是特征的数量；val()是对集合中特征值的预测；表示val第个特征的贡献。

2 结果与分析

2.1 年尺度预测结果对比

选取2018—2021年土壤10 ～ 40 cm深度含水量数据进行训练，基于RF、GBM算法构建土壤含水量预测模型。对比2种模型测试集的预测结果(表1)发现，10 ～ 40 cm深度预测精度相差较小，2差值都在0.1以内。GBM模型预测精度较高，10 ～ 40 cm深度2值均大于0.94，MAE和RMSE均值均小于0.006和0.026；RF模型预测精度略差，10 ～ 40 cm深度2均值范围为0.881 ～ 0.891，MAE和RMSE均值均小于0.054和0.071。

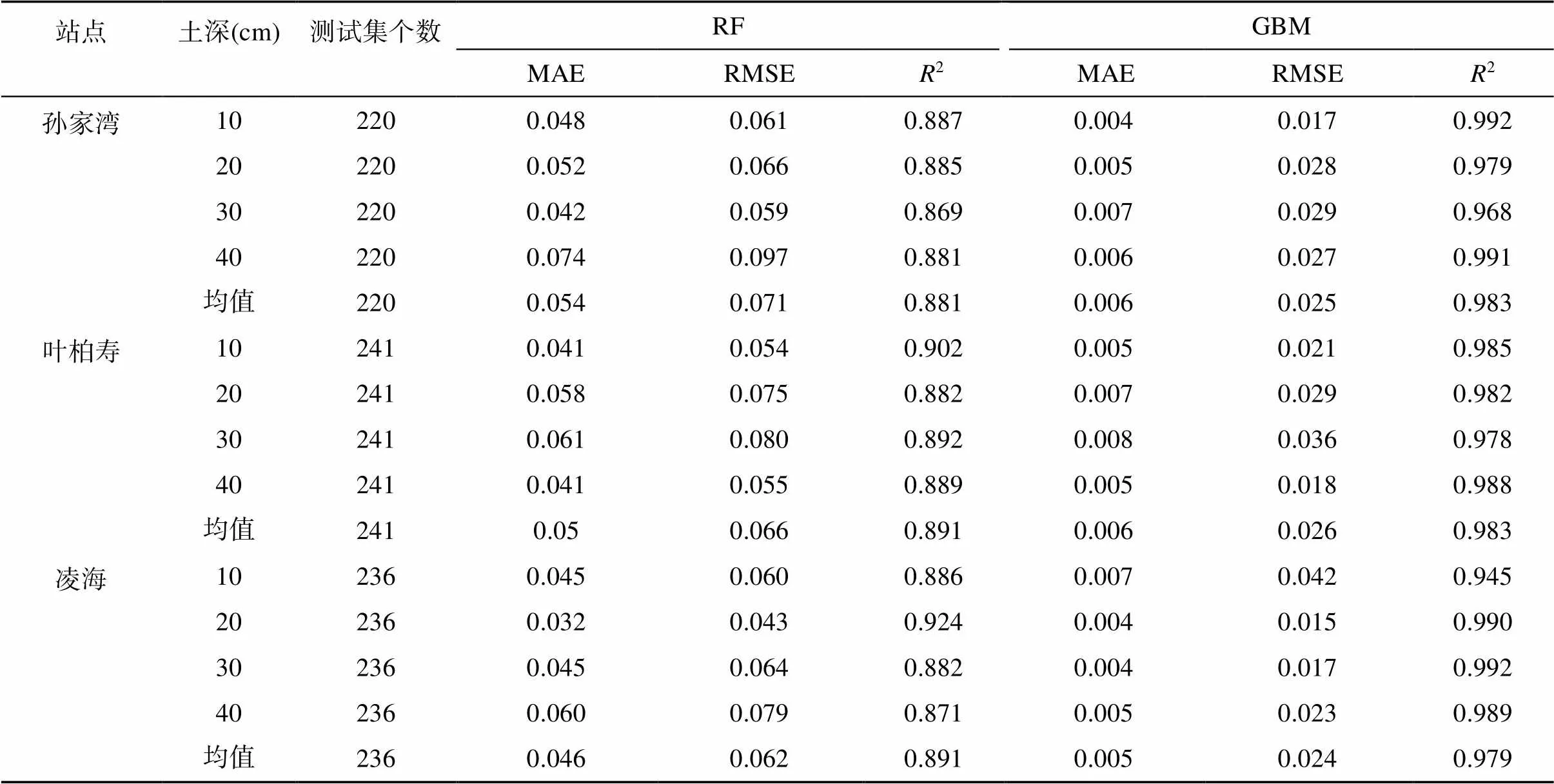
表1 年尺度下不同站点不同深度土壤含水量RF和GBM模型预测精度比较

以孙家湾站为例，2种模型10 ～ 40 cm深度测试集土壤含水量样本预测值与实测值基本都在1∶1线附近，2值均超过0.86，GBM模型的预测值明显更加接近实测值，如图2所示。综上所述，对比2种模型方法的评价指标，RF模型和GBM模型年尺度下均能精准地预测土壤含水量，但GBM模型表现更佳。

图2 孙家湾站10 ～ 40 cm深度土壤含水量预测值与实测值

2.2 季节尺度预测结果对比

本研究中，季节划分标准为：春季3—5月、夏季6—8月、秋季9—11月、冬季12月—次年2月。季节尺度的预测结果(表2)表明，GBM模型和RF模型在不同季节预测土壤含水量均具有较高的精度。GBM模型10 ～ 40 cm深度各季节2均值范围为0.931 ～ 0.938，MAE值均小于0.026，RMSE值均小于0.065；RF模型10 ～ 40 cm深度各季节2值范围为0.816 ～ 0.894，MAE值均小于0.073，RMSE值均小于0.095，精度略低于GBM模型。

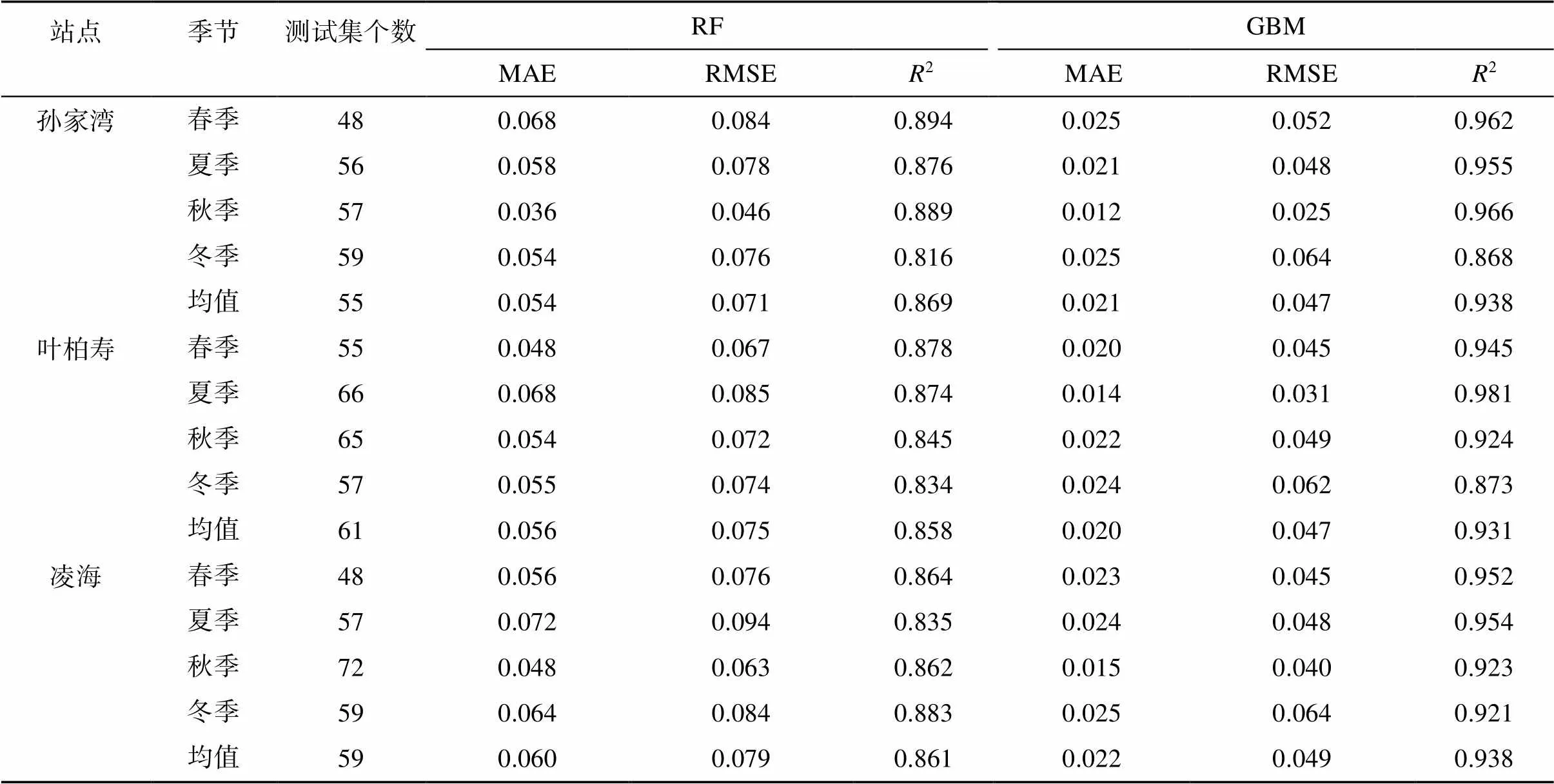
表2 不同季节土壤含水量2种模型预测精度比较

对比分析多时间尺度模型预测结果表明：GBM模型和RF模型在年、季尺度下均有较好的预测结果(2均大于0.816)，GBM模型的预测精度略高(2均大于0.868)。年尺度上，2种模型在3个站点不同土层的2均值皆大于0.881，RMSE均值皆小于0.071，MAE均值皆小于0.054；季节尺度上，2种模型在春季、夏季和秋季的预测结果则更好，春季、夏季和秋季2均大于0.835，RMSE均小于0.094，MAE均小于0.072。

2.3 特征要素贡献度分析

为探究不同时间尺度、不同深度各输入特征要素对预测的土壤含水量的贡献度，将预测结果较好的GBM模型与SHAP方法进行融合。分别计算年、季尺度下降水、日照时数、平均相对湿度、风速、平均气温这5个输入变量的SHAP值，并基于SHAP值大小判断输入特征对土壤含水量的贡献。

年尺度上，孙家湾站、叶柏寿站和凌海站10 ～ 40 cm深度特征要素贡献排序基本一致，均是平均气温贡献最大，降水贡献最小。其中叶柏寿站10、20和40 cm深度的特征要素贡献排序从高到低分别为平均气温、日照时数、相对湿度、风速和平均气温；30 cm深度则为平均气温、相对湿度、日照时数、风速和平均气温，如图3所示。孙家湾站和凌海站特征要素贡献排序与叶柏寿站一致。

为对比4个不同深度、不同季节5个输入特征对预测土壤含水量的整体贡献度，利用特征的SHAP值之和(整体SHAP值)来对比不同深度和季节的结果。

年尺度上，4个土层深度输入的5个气象要素对于预测10 cm和20 cm土层的土壤含水量贡献较大，且更适用于预测20 cm深度的土壤含水量。孙家湾、叶柏寿和凌海站10 cm和20 cm深度的整体SHAP值分别为7.99、8.07和7.98，比30 cm和40 cm深度分别增加了10.66%、12.08% 和1.01%。各站点20 cm深度输入变量的整体SHAP值分别为8.48、8.43和8.53，比10 cm深度分别增加了12.96%、14.48% 和14.79%，其中叶柏寿站SHAP值如图3所示。

由于年尺度20 cm土层整体SHAP值最高，因此季节尺度上选择20 cm土层为代表性土层进行分析。孙家湾站和叶柏寿站贡献最大的特征要素是日照时数，凌海站为平均气温，所有站点对预测结果贡献最低的变量均为降水。夏季整体SHAP值高于其余3个季节，其中叶柏寿站春季、秋季和冬季整体SHAP值相比夏季分别降低36.5%、18.8% 和46.2%；凌海站分别降低47.9%、10.8% 和5.8%；孙家湾站春季整体SHAP值比夏季增加2.6%，秋季和冬季分别降低39.6% 和26.6%，具体结果见表3。

图3 叶柏寿站10 ～ 40 cm土壤预测含水量的特征要素贡献分布

在年、季尺度上降水贡献均最低，可能有以下两个方面的原因：①辽西地区年降水量区间为400 ～ 700 mm，且全年2/3的降水集中在夏季。孙家湾、叶柏寿和凌海站夏季降水量分别为319.3、357.2和474.43 mm；②无降水日数占比较高。孙家湾、叶柏寿和凌海站年内无降水日数的数据占比分别为81.1%、79.4% 和79.5%；尽管降水集中在夏季，但无雨日数仍高于60%(孙家湾、叶柏寿和凌海站占比分别为61.8%、62.0% 和62.3%)。

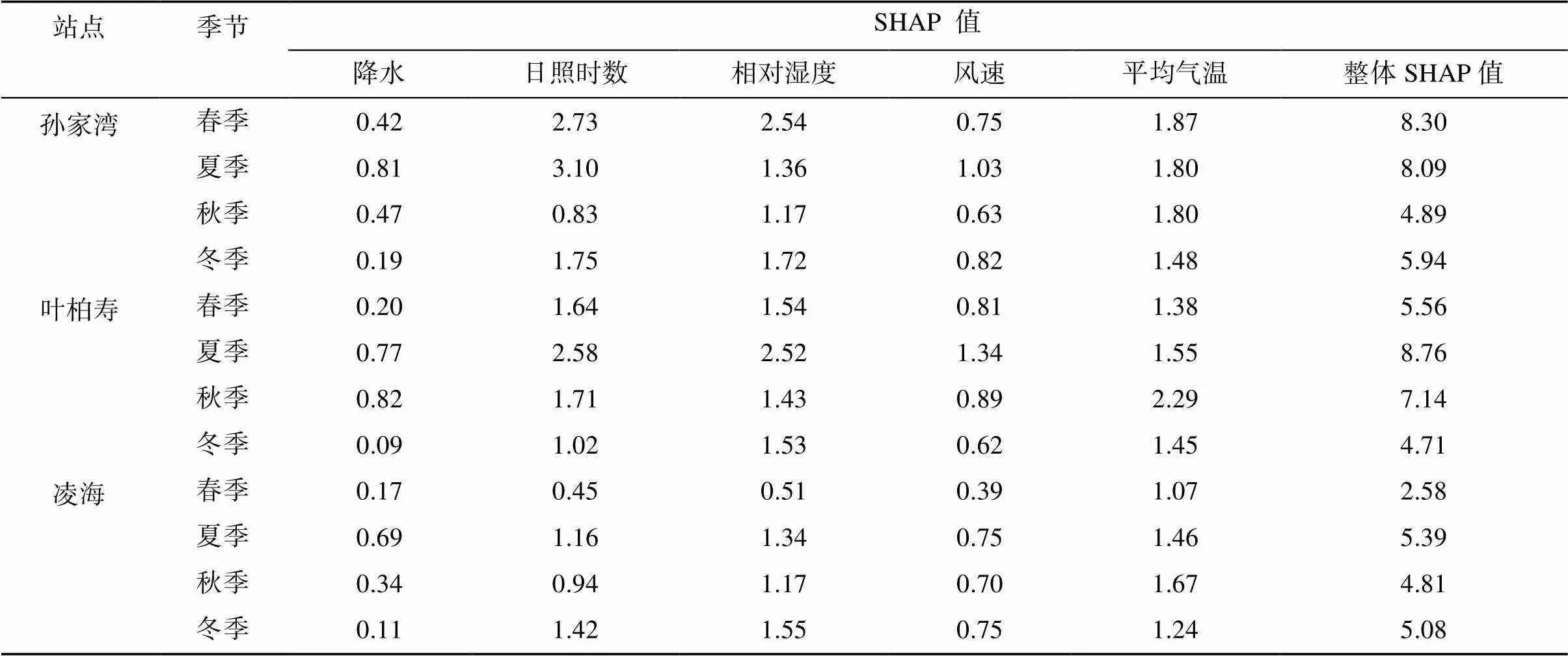
表3 20 cm深度土壤预测含水量不同季节特征要素贡献统计

集成学习预测结果的准确性与样本数量和数值变化区间成正比，因此在相同数量样本条件下，较多的无降水日数可使降水贡献小于其他要素。虽然5个特征中降水的贡献最低，但对比季节贡献结果可以看出，降水对土壤含水量的贡献度与降水量成正比关系。辽西地区夏季降水最多，贡献度也是四季最高，如图4所示。

综上所述，辽西地区降水对土壤含水量贡献较低的主要原因是年内、季节内降水分布不均。已有的研究也表明，降水对于土壤含水量的贡献较小。Clewley等[26]利用RF分析了高程、坡度和降水等对土壤水分的影响，结果表明降水影响最小；Karthikeyan和Mishra[27]利用XGBoost算法分析了海拔、土壤质地、归一化植被指数(NDVI)和降水对于土壤水分的影响，结果表明降水影响最小。以上研究利用了不同的算法、输入了不同的变量来预测土壤含水量，但结果都表明降水对于土壤水分的影响最小。

图4 2018—2021年不同季节累积降水量和SHAP值

为定量识别不同输入特征要素对应的有效阈值区间，制定区间识别划分规则为：①筛选出SHAP值大于0的点，提取点所在的区间；②将区间等分，分别计算每个区间SHAP均值；③比较划分后的区间与原区间SHAP均值的大小，最终定量识别不同输入特征对土壤含水量贡献最大的区间。各个特征SHAP值大于0的区间分别为降水0 ～ 10 mm、日照时数0 ～ 8 h、相对湿度60% ～ 80%、风速1 ～ 3 m/s、气温22 ～ 24℃，如图5所示。

图5 特征要素贡献依赖图

孙家湾站和叶柏寿站对土壤含水量贡献最大的特征区间一致，都是日照时数贡献最大，最大区间为2 ～ 4 h；降水贡献最小，贡献最大区间为0 ～ 5 mm。凌海站却是降水贡献最大，贡献最大的区间为5 ～ 10 mm；风速贡献最小，贡献最大的区间为1 ～ 2 m/s。各站点特征区间SHAP均值见表4。

表4 3站点各个特征要素区间SHAP均值

注：表中加粗部分即各个特征要素贡献最大值，所在区间为贡献最大区间。

3 讨论

本研究结果表明，GBM模型在年、季尺度上的预测精度均高于RF模型(2均大于0.816)。融合SHAP方法的GBM模型不仅定量计算出了不同土层、不同季节输入变量对土壤含水量的贡献，而且基于区间划分规则识别了特征最大贡献区间。为验证该模型在预测土壤含水量上的优势，从以下两方面进行讨论。

1)与神经网络中最常用的多层感知机(MLP)进行对比验证。目前利用神经网络预测土壤含水量的研究较多[28]，为了验证GBM模型和RF模型在预测土壤含水量上的优势，采用神经网络中最常用的MLP模型进行对比验证。利用optuna方法[29]对MLP进行10次参数择优后，最终确定神经网络隐藏层分别为70、60和20，最优参数分别为activation='relu'，solver='lbfgs'，max_iter=1400，alpha=0.04。基于参数优选后的结果预测各站点不同深度土壤含水量结果，3个站点的MAE介于0.065 ～ 0.110，RMSE介于0.086 ～ 0.146，2介于0.423 ～ 0.871，具体结果见表5。MLP模型的预测精度明显低于本研究中构建的2种土壤含水量预测模型，GBM模型在3个站点的2均值分别提升了0.226、0.176和0.459；RF模型在3个站点的2均值分别提升了0.124、0.084和0.371。上述结果表明，本研究使用的集成学习模型相较于MLP模型具有显著的优势。

2)与国内外同类研究结果对比。已有的研究也表明，GBM模型和RF模型在土壤含水量预测方面拥有更加良好的表现。Chen[8]等基于RADARSAT-2和Sentinel-2数据，使用支持向量回归机(SVR)、RF和梯度提升决策树(GBDT)这3种机器学习方法在加拿大安大略省西南部对冬小麦种植区0 ～ 5 cm土壤水分进行预测，结果表明，RF模型结果最优(2为0.94)，GBMT模型次之(2为0.77)，SVR模型结果最差(2为3.06)。

表5 MLP模型对10 ～ 40 cm深度土壤含水量的预测结果

目前针对特征贡献的研究还相对较少。Clewley等[26]采集了位于加拿大马尼托巴省南部SMAP实验点2012年6—7月间13 d现场数据，利用RF算法计算了各输入特征的重要度，结果表明，贡献最大的变量是高程，贡献最小的变量是降水；Cai等[30]分析了各输入特征与土壤含水量的相关性，结果表明，相对湿度相关性最大，降水相关性最小。本研究利用SHAP方法不仅判断出不同时间尺度下最大贡献的特征要素，而且制定了区间划分规则识别输入特征最大贡献区间，从方法应用范围上进行了提升和改进。

4 结论

本文基于集成学习Bagging中的随机森林(RF)、Boosting中的梯度提升机(GBM)，研究了2种算法在辽西地区预测土壤含水量的适用性。在土壤含水量预测的基础上，引入SHAP方法定量计算输入特征变量对土壤含水量的贡献，并基于制定的区间划分规则识别特征最大贡献的阈值范围，实现了高精度可解释的土壤水分预测。

1)从模型适用性方面，GBM模型更适合辽西地区的土壤含水量预测。年、季尺度下，GBM模型和RF模型均适用于辽西地区土壤含水量预测。年尺度下GBM模型和RF模型10 ～ 40 cm深度2分别为0.982、0.888；季节尺度下2分别为0.935、0.863。

2)对比分析降水、日照时数、平均相对湿度、风速、平均气温5个输入要素的贡献度，气温和日照时数贡献较大，其中气温贡献最大范围21 ～ 23℃；日照时数贡献最大范围为2 ～ 4 h。年尺度下，气温贡献最大，降水贡献最小；季节尺度下，夏季对于土壤含水量预测的贡献最大，贡献最大的特征要素为日照时数，贡献最小的特征要素为降水。

3)与传统的MLP模型结果相比，GBM模型和RF模型10 ～ 40 cm深度土壤含水量的预测结果均优于MLP模型。孙家湾站、叶柏寿站和凌海站GBM模型的2均值相较于MLP模型分别提升了0.226、0.176和0.459，RF模型较之提升了0.124、0.084和0.371。

4)本研究首次将集成学习算法中的GBM模型和RF模型应用到辽西地区的土壤含水量预测，验证了2种模型在年、季尺度上的有效性。创新引入SHAP方法，定量化表征输入特征要素贡献度，并基于制定的区间划分规则计算了区间SHAP均值，识别了输入特征最大贡献区间，可为其他地区的土壤含水量预测研究提供新的参考与借鉴。

[1] Zhang D J, Zhou G Q. Estimation of soil moisture from optical and thermal remote sensing: A review[J]. Sensors (Basel, Switzerland), 2016, 16(8): 1308.

[2] 程谅, 焦雄, 邸涵悦, 等. 不同整地措施坡面土壤水分时空分布特征[J]. 土壤学报, 2021, 58(6): 1423–1435.

[3] Hummel J W, Sudduth K A, Hollinger S E. Soil moisture and organic matter prediction of surface and subsurface soils using an NIR soil sensor[J]. Computers and Electronics in Agriculture, 2001, 32(2): 149–165.

[4] 周良臣. 利用土壤水动力学模型预测麦田土壤水分的研究[J]. 节水灌溉, 2007(3): 10–13, 17.

[5] 白冬妹, 郭满才, 郭忠升, 等. 时间序列自回归模型在土壤水分预测中的应用研究[J]. 中国水土保持, 2014(2): 42–45, 69.

[6] 聂红梅, 杨联安, 李新尧, 等. 基于PCA-SVR的冬小麦土壤水分预测[J]. 土壤, 2018, 50(4): 812–818.

[7] Padarian J, Minasny B, McBratney A B. Machine learning and soil sciences: A review aided by machine learning tools[J]. SOIL, 2020, 6(1): 35–52.

[8] Chen L, Xing M F, He B B, et al. Estimating soil moisture over winter wheat fields during growing season using machine-learning methods[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 3706–3718.

[9] Zhang L Q, Liu Y, Ren L L, et al. Analysis of flash droughts in China using machine learning[J]. Hydrology and Earth System Sciences, 2022, 26(12): 3241–3261.

[10] Feng P Y, Wang B, Liu L D, et al. Machine learning-based integration of remotely-sensed drought factors can improve the estimation of agricultural drought in South-Eastern Australia[J]. Agricultural Systems, 2019, 173: 303–316.

[11] Cai J C, Xu K, Zhu Y H, et al. Prediction and analysis of net ecosystem carbon exchange based on gradient boosting regression and random forest[J]. Applied Energy, 2020, 262: 114566.

[12] Prodhan F A, Zhang J H, Sharma T P P, et al. Projection of future drought and its impact on simulated crop yield over South Asia using ensemble machine learning approach[J]. Science of the Total Environment, 2022, 807: 151029.

[13] Lundberg S M, Lee S I. A unified approach to interpreting model predictions[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. December 4 - 9, 2017, Long Beach, California, USA. New York: ACM, 2017: 4768–4777.

[14] 王鑫, 廖彬, 李敏, 等. 融合LightGBM与SHAP的糖尿病预测及其特征分析方法[J]. 小型微型计算机系统, 2022, 43(9): 1877–1885.

[15] Kannangara K K, Zhou W H, Ding Z, et al. Investigation of feature contribution to shield tunneling-induced settlement using Shapley additive explanations method [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2002, 14(4): 1052–1063.

[16] Zhang K, Xu P D, Zhang J. Explainable AI in deep reinforcement learning models: A SHAP method applied in power system emergency control[C]//2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2). October 30 - November 1, 2020, Wuhan, China. IEEE, 2021: 711–716.

[17] Wang D, Thunéll S, Lindberg U, et al. Towards better process management in wastewater treatment plants: Process analytics based on SHAP values for tree-based machine learning methods[J]. Journal of Environmental Management, 2022, 301: 113941.

[18] Fukas P, Rebstadt J, Menzel L, et al. Towards explainable artificial intelligence in financial fraud detection: Using shapley additive explanations to explore feature importance[C]//Advanced Information Systems Engineering: 34th International Conference, CAiSE 2022, Leuven, Belgium, June 6-10, 2022, Proceedings. New York: ACM, 2022: 109–126.

[19] 王笑歌. 辽西地区干旱评价及预测研究[D]. 沈阳: 沈阳农业大学, 2019.

[20] 余东行, 张保明, 赵传, 等. 联合卷积神经网络与集成学习的遥感影像场景分类[J]. 遥感学报, 2020, 24(6): 717场727.

[21] Friedman J H. Greedy function approximation: A gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189–1232.

[22] 万伦军. 基于梯度提升模型的负相关学习算法的研究与应用[D]. 合肥: 中国科学技术大学, 2014.

[23] Memon N, Patel S B, Patel D P. Comparative analysis of artificial neural network and XGBoost algorithm for PolSAR image classification[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2019: 452–460.

[24] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5–32.

[25] 蔡庆空, 李二俊, 陶亮亮, 等. 基于改进作物散射模型的陕西杨凌区麦田土壤水分反演研究[J]. 土壤, 2020, 52(4): 846–852.

[26] Clewley D, Whitcomb J B, Akbar R, et al. A method for upscalingsoil moisture measurements to satellite footprint scale using random forests[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(6): 2663–2673.

[27] Karthikeyan L, Mishra A K. Multi-layer high-resolution soil moisture estimation using machine learning over the United States[J]. Remote Sensing of Environment, 2021, 266: 112706.

[28] 范嘉智, 谭诗琪, 罗宇, 等. 长短期记忆神经网络在多时次土壤水分动态预测中的应用[J]. 土壤, 2021, 53(1): 209–216.

[29] Akiba T, Sano S, Yanase T, et al. Optuna: A next-generation hyperparameter optimization framework[C]// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. August 4 - 8, 2019, Anchorage, AK, USA. New York: ACM, 2019: 2623–2631.

[30] Cai Y, Zheng W G, Zhang X, et al. Research on soil moisture prediction model based on deep learning[J]. PLoS One, 2019, 14(4): e0214508.

Prediction of Soil Moisture Content Based on Ensemble Learning—A Case Study of Western Liaoning Province

FU Pingfan1,2, YANG Xiaojing1,2*, SU Zhicheng1,2, QU Yanping1,2, MA Miaomiao1,2

(1 China Institute of Water Resources and Hydropower Research, Beijing 100038, China; 2 Research Center of Flood Control, Drought Relief, and Mitigation Engineering, Ministry of Water Resources, Beijing 100038, China)

Accurate and efficient prediction of soil moisture content (SMC) is vital for field water management. In this study, two types of ensemble learning models (RF and GBM) were used to compare their applicability in SMC prediction based on the automatic hourly SMC data at 10–40 cm during 2018—2021 from three self-built sites in the western Liaoning area, the prediction results were also compared and verified at annual and seasonal scales. The SHAP (Shapley Additive Explanations) method was introduced to quantitatively characterize the effects of five input variables (precipitation, sunshine hour, average relative humidity, wind speed and average temperature) on SMC prediction. Interval division rules were developed to identify the interval of maximum contribution threshold of variables. The results show that2of GBM and RF models are 0.982 and 0.888 respectively on annual scale, temperature is the most important factor with the maximum contribution range of 21–23℃, whileRof the two models are 0.935 and 0.863 respectively on seasonal scale, sunshine hour is the most important factor with the maximum contribution range of 2–4 hours. This study innovatively applied SHAP method to analyze the contribution rates of input variables of machine learning, and verified the results of RF and GBM methods in SMC prediction, which can provide reference for related study on SMC.

Ensemble learning; Soil moisture content forecasting; Gradient boosting machine; Random forest; Western Liaoning; SHAP value

S152.7

A

10.13758/j.cnki.tr.2023.03.025

付平凡, 杨晓静, 苏志诚, 等. 基于集成学习的土壤含水量预测研究——以辽西地区为例. 土壤, 2023, 55(3): 671–681.

江西省“科技+水利”联合计划项目(2022KSG01002)和中国水利水电科学研究院防洪抗旱减灾工程技术研究中心青年创新人才推进项目资助。

(yxj@iwhr.com)

付平凡(1998—)，男，河南信阳人，硕士研究生，主要从事干旱监测研究。E-mail: fupf123456@163.com