基于单一和集合土壤转换函数模型对土壤含水量的模拟性能分析①
2023-08-02陈文娟石文豪孙少波张永根
李 奇,陈文娟,石文豪,孙少波,张永根*
基于单一和集合土壤转换函数模型对土壤含水量的模拟性能分析①
李 奇1, 2,陈文娟1, 2,石文豪1, 2,孙少波1, 2,张永根1, 2*
(1天津大学地球系统科学学院表层地球系统科学研究院,天津 300072;2天津市环渤海关键带科学与可持续发展重点实验室,天津 300072)
以海河流域3个实验场地(密云站、大兴站、馆陶站)为研究区,采用7种常用的单一土壤转换函数(soil pedotransfer function,PTF)模型预测土壤水力参数作为HYDRUS-1D的模型参数,求解Richards方程获得土壤含水量,并与实测土壤含水量进行比较,评价了常用单一PTF模型预测的土壤水力参数对土壤含水量的模拟性能。此外,采用3种方法构建集合PTF模型,评价了集合PTF模型对土壤含水量的模拟性能。结果表明:基于van Genuchten方程构建的单一PTF作为模型参数模拟土壤含水量的均方根误差最小;而其中Rosetta3模型表现更优。在集合PTF模型中,基于贝叶斯平均法构建的模型表现最好。集合PTF模型预测土壤水力参数可以较好地捕捉多个单一PTF预测土壤水力参数的整体趋势,弥补单一PTF在某些情况下模拟误差较大的不足。
土壤转换函数;土壤水力参数;HYDRUS-1D;集合模型;贝叶斯平均法
土壤水是陆地水循环的重要组成部分,精确刻画土壤水分运动及溶质运移过程,对于模拟土壤中污染物的迁移转化过程[1]、开展流域水文过程模拟[2]、研究作物的生长发育[3]、制定合理的灌溉制度[4]等方面都具有重要意义。精确模拟土壤水分运动过程需要准确量化土壤水力参数,即土壤水分特征曲线和导水率曲线[5-6]。目前获得土壤水力参数的方法主要有直接测定法和间接预测法。直接测定法是通过野外采样,在实验室利用压力膜仪或离心机等仪器进行测定[7]。但是测量过程繁琐、耗时费力,当研究区域较大时,仅采用室内实验测量土壤水力参数不足以描述大尺度土壤水分运动过程。间接预测法如利用土壤转换函数(pedotransfer function,PTF),通过构建土壤较容易测得的基本属性(如土壤颗粒成分、容重、有机质含量等)与土壤水力参数之间的经验关系,来预测土壤水分特征曲线与导水率曲线[8-10]。此方法可弥补野外采样试验空间代表性不足等问题,是一种高效获得土壤水力参数的方法。
在过去的几十年里,许多学者基于不同地区的数据集构建了不同的PTF[11-12]。评价PTF的优劣不仅需要衡量预测的土壤水力参数与实测值的误差,更重要的是需要检验预测的土壤水力参数在非饱和带水流运动模型(如Richards方程)中能否准确模拟土壤含水量或土壤基质势的动态过程。然而不同PTF的构建依赖于所采用的数据库,具有特有属性范围,而在应用中有其适用范围[13-17]。Dai等[18]指出绝大多数PTF没有提供其适用范围,因而在其构建地区之外的预测精度通常是未知的。
此外,使用单一PTF预测土壤水力参数可能会导致对预测参数不确定性的低估和对预测性能的高估,从而对预测结果产生系统偏差[19];由于土壤具有强烈的空间异质性,单一PTF常基于某一区域数据集进行构建,从而导致单一PTF在实际应用中具有明显的偏差。
目前,集合模型已成为预测天气和开展气候变化研究的常用方法,然而,集合模型尚未在预测土壤水力参数及研究土壤水分运动过程中广泛使用[20]。集合模型是综合利用各种方法提供的信息,以适当的方式构建集合模拟与单一模拟预测值之间的关系,从而改善模型的预测能力。研究表明集合模型可以提高模型的预测精度,降低模型预测的不确定性[21-22]。Guber等[23]比较了不同方法构建的集合PTF模型,指出构建集合PTF模型预测土壤水力参数,其关键之处在于如何为每种PTF分配适当的权重。集合模型分配权重方法主要有两种,第一种是平均权重法,第二种是根据模拟值与实测值的差距大小动态分配权重,目前主要有以下方法:贝叶斯平均法[24]、基于回归分析的超集合预报法[25]、赤池信息准则法(Akaike information criterion,AIC)[26]等。Zhang等[27]基于全球土壤数据库NCSS评价了13种不同单一PTF模型利用土壤基本物理性质预测土壤水力参数的性能,利用贝叶斯平均法构建了集合PTF模型。结果表明集合PTF模型预测土壤水力参数的性能优于单一PTF模型,但其并未探究集合PTF模型对土壤含水量模拟性能的影响。
本研究的目的是在前人研究成果基础上,基于海河流域3个通量站观测数据,探究不同单一PTF预测的土壤水力参数在非饱和带水流运动模型中对土壤含水量动态过程模拟结果的影响,在此基础上构建3种集合PTF模型预测土壤水力参数,进一步探究集合PTF模型对土壤含水量模拟性能的影响,比较不同构建集合PTF模型方法的优劣。研究成果可为精确模拟土壤水分运动过程,进而为精确高效开展流域水文过程等模拟提供参考和依据。
1 材料与方法
1.1 站点和数据描述
本研究选取海河流域具有连续观测土壤含水量数据的3个通量站开展研究,分别是密云站[28](位于北京市密云县新城子镇,观测点的经纬度117.3233°E、40.6308°N)、大兴站[29](位于北京市大兴区魏善庄,观测点的经纬度116.4271°E、39.6213°N)、馆陶站[30](位于河北省馆陶县河寨村,观测点的经纬度115.1274°E、36.5150°N)。3个站点都含有2008—2010年自动气象站数据和涡动相关仪数据[31-32]。土壤含水量和降水数据每10 min输出一次,其中土壤含水量观测的深度分别是5、10、20、40、60、100 cm。潜热通量(用于计算蒸发量)数据每30 min输出一次。为便于模拟,须保证潜热通量、降水以及各深度土壤含水量观测值在一段时间内是连续不缺失的,同时为了研究降水对土壤含水量变化的影响,没有选择冬季降水较少的时段。经过筛选,本文截取出密云站2010年8月1日至9月30日(61 d)、大兴站2010年5月1日至6月18日(49 d)以及馆陶站2010年6月1日至7月31日(61 d)100 cm深度以内的土壤含水量展开模拟研究。
1.2 土壤水分特征曲线模型与土壤转换函数(PTF)
本研究使用的土壤水分特征曲线模型包括Brooks- Corey(BC)方程[33]和van Genuchten(VG)方程[34],两个方程的表示形式如下:


式中:r、s分别为土壤残余含水量和土壤饱和含水量(cm3/cm3),b为土壤进气值(cm),是与土壤孔隙尺寸分布有关的参数,是与土壤进气值倒数相关的参数(cm–1),是形状参数,与土壤孔隙分布有关(无量纲)。
本研究总共选取了7种常用的PTF模型(主要基于相应文章的引用次数)来计算上述水力参数,开展集合PTF模型的研究。其中3种PTF计算基于BC方程的水力参数,4种PTF计算基于VG方程构建的水力参数。此外,还有许多候选PTF未加入集合模型中,如Carsel[35]、Williams[36]、Tomasella[37]、Saxton[38]等。没有选择这些PTF的主要原因:一是这些PTF为查表型的PTF,而本文使用的PTF为参数PTF,可提供土壤水分特征曲线或导水率曲线的数学表达式,进而获得任意土壤水吸力下的土壤含水量值;二是Williams等PTF预测的参数在运行HYDRUS-1D时,会出现不收敛的情况。表1展示了所选的PTF、输入因子以及相应的PTF在谷歌学术的引用次数。为了清楚表示本文中使用的PTF土壤基本属性的差异,还对涉及的7个单一PTF构建时使用的土壤基本属性信息进行了整理,见表2。
1.3 数值模拟
HYDRUS-1D[46-47]利用有限元法求解Richards方程,该程序可以模拟各种条件下的土壤含水量变化,土壤水分特征曲线模型可以选择BC方程或者VG方程。
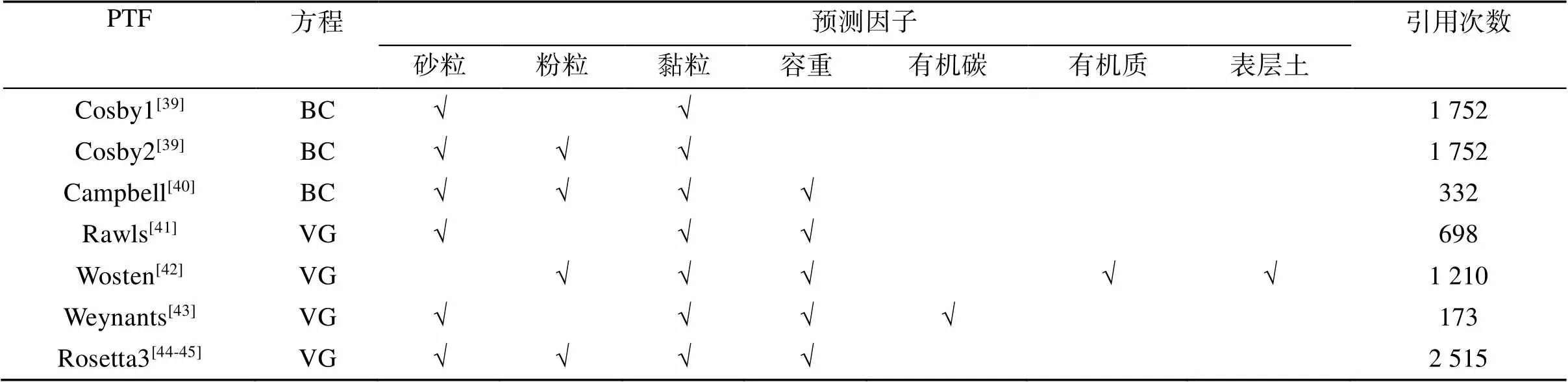
表1 7种PTF所采用的方程、输入因子和引用次数等信息
注:引用次数截止至2021年11月30日;Cosby1和Cosby2是Cosby等[39]根据美国23个州1 448个土壤样品分别使用单变量和两个独立变量进行回归分析构建的不同PTF。

表2 构建各PTF的土壤基本属性信息
注:“–”代表PTF没有使用该预测因子,“未提供”表示相关论文未提供土壤基本属性信息;“%”为质量百分数。
对于初始条件,本研究对模拟期第一天观测的5、10、20、40、60、100 cm土壤含水量按空间间隔为1 cm进行线性插值得到初始土壤含水量剖面。
对于边界条件,下边界因未达到潜水层,设置为自由排水边界。通过设置降水和潜在蒸散发来定义上边界条件,其中降水来自自动气象站观测数据,而潜在蒸散发ETp则采用HYDRUS-1D默认的Hargreaves公式计算,具体公式如下:

式中:ETp为潜在蒸发量(mm/d);a为外空辐射(J/(m2·s)),是与站点纬度有关的函数;m为日均温度(℃);TR为日最高温度与最低温度之差(℃)。温度等相关数据可以从自动气象站观测数据获取。
此外,HYDRUS-1D采用以下方法划分潜在蒸腾量p和土壤蒸发量p,具体公式如下:
p= ETp(1 – e–LAI)(4)
p= ETp· e–LAI(5)
式中:ETp为潜在蒸发量(mm/d),LAI为叶面积指数,为冠层消光系数,通常取0.39[47]。根据所选模拟期的时间段,参考相关研究[48],大兴站玉米还未生长,LAI取2.5;馆陶站玉米处于生长期,LAI取3.5;密云站玉米生长完成,LAI取4.5。
同一个站点(密云、大兴、馆陶)所对应的初始条件和边界条件设置相同。根系吸水采用HYDRUS-1D默认的Feddes模型。表3为站点土壤质地、土壤容重、土壤有机碳含量等信息[49],3个站点的土壤主要是棕壤与潮土,在实地取样时根据剖面上土壤机械组成和作物根系分布来确定土壤分层,将土壤分为3层:表层、根区层和底层。土壤水力参数的设置根据表3利用表1中7种PTF计算相应的土壤水力参数,之后运行HYDRUS-1D来模拟100 cm深度内的土壤含水量变化。为了直接反映不同PTF提供的土壤水力参数对土壤含水量模拟结果的影响,本文没有采用传统的基于土壤含水量观测值率定和优化土壤水力参数的方法,而是直接将不同PTF提供的土壤水力参数作为HYDRUS-1D的输入参数,开展模拟研究,进而分析不同PTF提供的水力参数对土壤含水量模拟结果的影响。

表3 三个站点的土壤质地和容重以及从SoilGrids提取的有机质信息
注:由于3个站点没有提供有机碳信息,因此选择从分辨率为250 m的SoilGrids全球栅格土壤有机碳地图[50]中提取对应坐标和深度所对应的土壤有机碳含量信息,根据土壤有机碳含量乘以换算系数1.7得到土壤有机质含量[51]。土壤粒径分析采用吸液管法获取土壤颗粒组成,测试结果为质量百分数(%)。
1.4 集合PTF模型的构建方法
本研究中采用了3种方法为每个PTF分配权重,第一种平均权重法[52]是一种简单的权重分配方法,给7种PTF赋予相同的权重,公式如下:
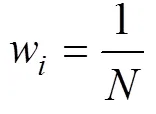
式中:表示第种PTF,总数为(本研究中= 7),w为第种PTF的权重。
第二种方法是方差倒数法[43],基于观测数据和模拟结果为每个PTF赋予权重,模拟结果与相应的观测值相差较大的PTF会被赋予较小的权重,通过以下公式实现:
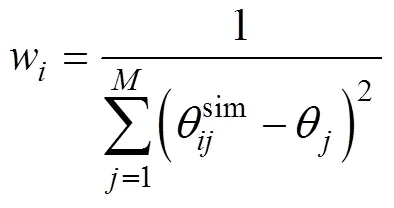
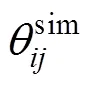
第三种方法是贝叶斯平均法,即基于观测数据通过优化算法,如遗传算法[53](genetic algorithm,GA)计算每种PTF的权重,这是一种权重分配的优化算法,同样基于数据驱动,会给模拟土壤含水量效果较好的PTF分配更高的权重。该方法通过使公式(8)达到最小值来实现。
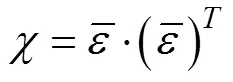

通过上述3种方法计算出每种PTF的权重后,为了确保权重之和等于1,首先对权重进行标准化,之后利用公式(10)计算出加权后的土壤含水量est作为集合PTF模型的土壤含水量模拟值。

1.5 评价指标
模型评价指标采用土壤含水量观测值和模拟值的均方根误差(RMSE)来表示,如公式(11)所示。
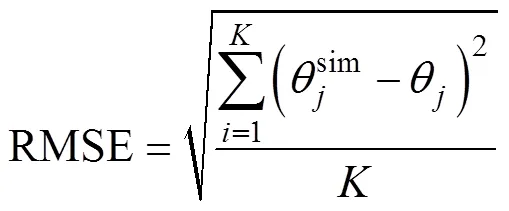
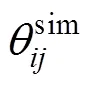
2 结果与分析
2.1 单一PTF模拟结果比较
图1展示了利用不同单一PTF提供的水力参数作为模型参数运行HYDRUS-1D所模拟的土壤含水量与站点对应观测值的对比结果。整体来看,HYDRUS-1D所模拟的土壤含水量与站点观测值在变化趋势上大致相同,7种PTF提供的土壤水力参数在一定程度上均能反映出3个站点不同深度土壤含水量随时间的变化情况。
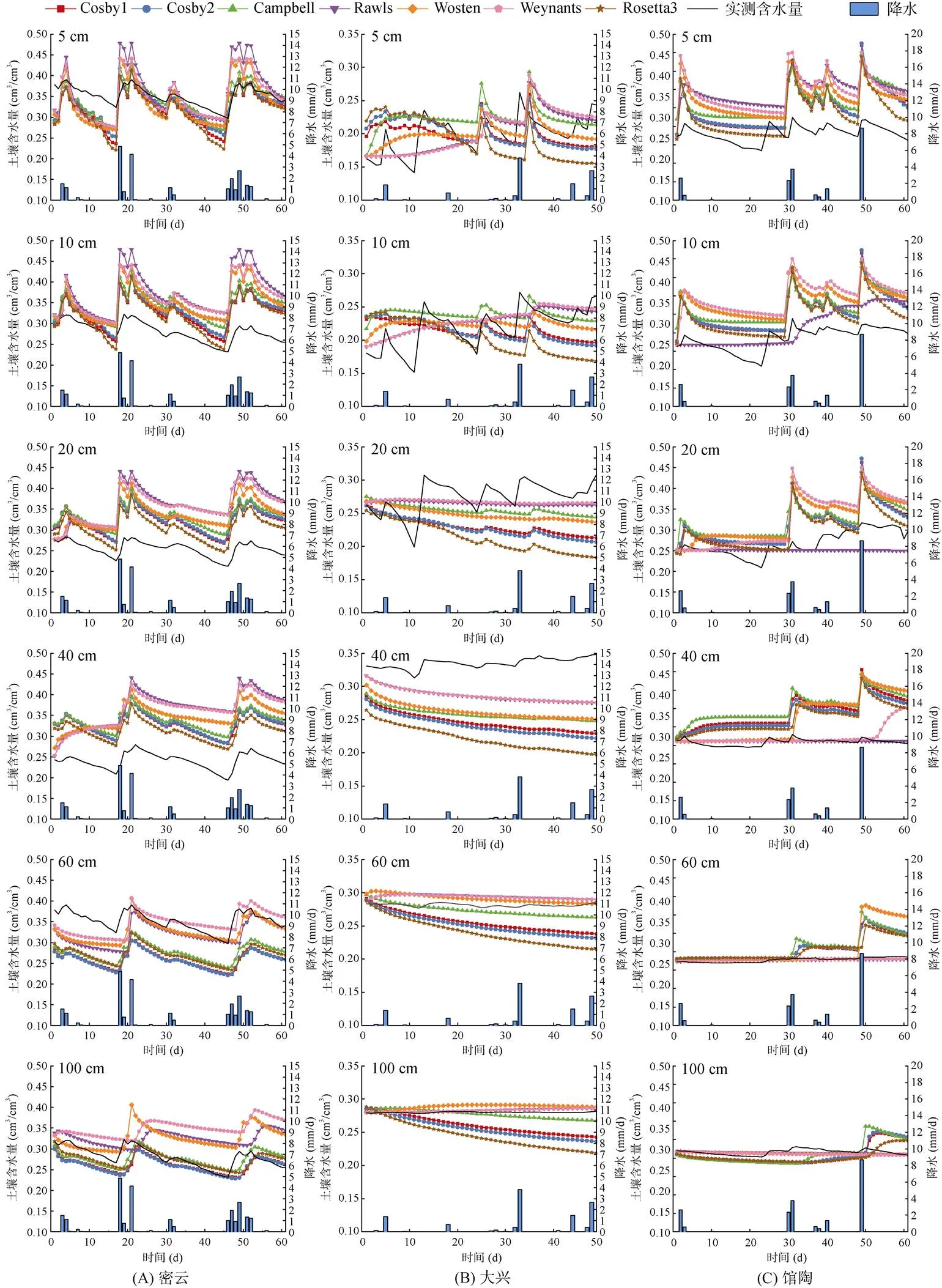
图1 密云站、大兴站、馆陶站基于单一PTF模拟的土壤含水量模拟值及实测值随时间变化图
0 ~ 20 cm的土壤(包括5、10、20 cm 3个深度)靠近地表,容易受到降水、入渗、蒸发和人为活动等各方面影响,在各个降水时段土壤含水量的变化都较为明显且幅度较大,土壤含水量受降水的影响尤其明显,土壤含水量峰值与降水时间显示出很好的同步性。而40 ~ 100 cm土壤含水量随时间变化较为稳定,受降水和蒸发的影响较小。
此外,除个别PTF在某些深度(如基于Rawls的PTF在馆陶站10、20 cm处,基于Weynants的PTF在馆陶站40 cm处)与其他PTF模拟出的土壤含水量不同外,大部分PTF计算的土壤水力参数模拟出的土壤含水量时间序列与实测值近乎平行,相关性较好,只是存在不同程度的位移。图2以密云站为例,展示了不同PTF计算的含水量时间序列之间的相关系数矩阵,颜色越深,圆圈越大,代表相关性越强。其中43%的模拟值之间的相关系数超过0.95,没有小于0.5的相关系数。表明本研究中所选择的PTF计算的土壤水力参数运行HYDRUS-1D得到了相关性较高的土壤含水量模拟结果。
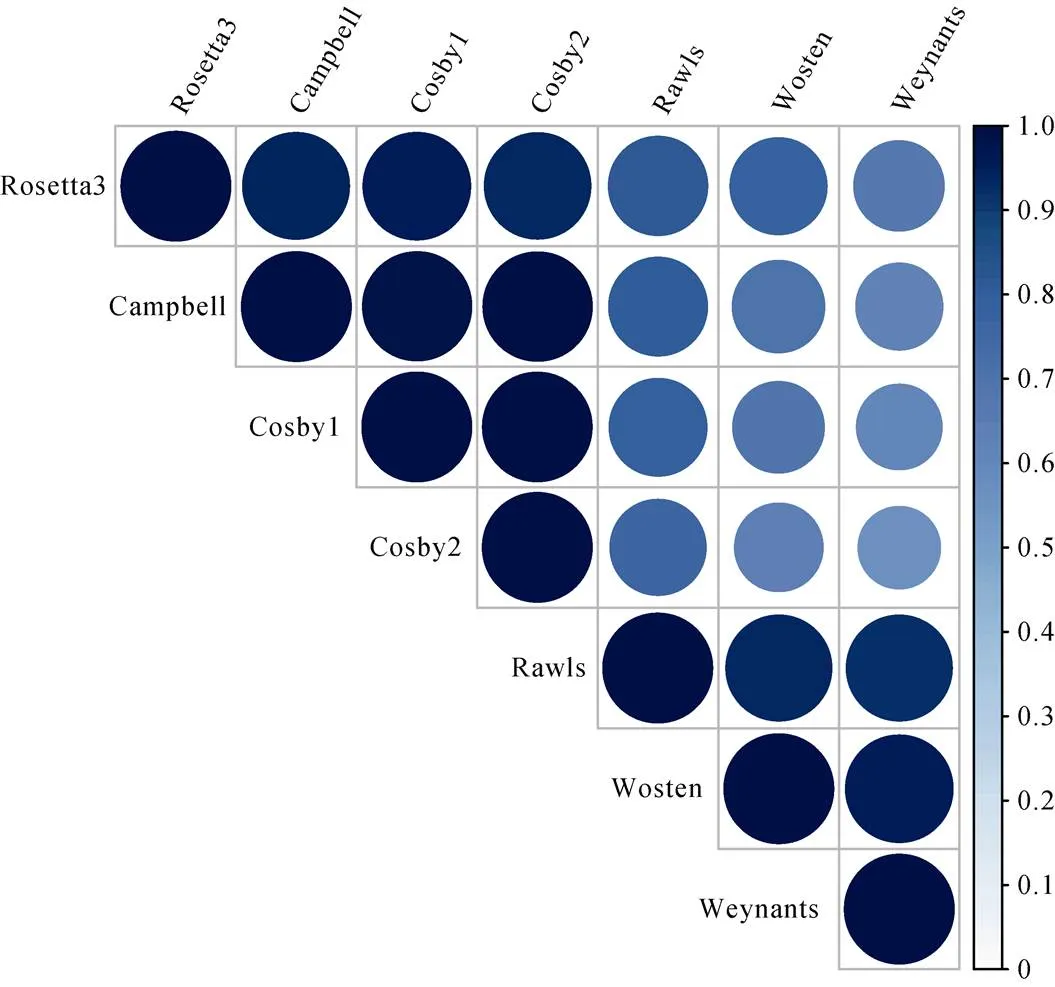
图2 基于7种PTF模拟出的土壤含水量时间序列的斯皮尔曼相关系数矩阵图(以密云站为例)
2.2 单一PTF模拟结果误差分析
密云站在10 ~ 40 cm深度处(包括10、20、40 cm 3个深度的观测值)的含水量模拟值与实测值相对普遍偏高,造成这种情况可能有两个原因:①站点下垫面主要是果树,对降水存在截留作用,而模拟过程没有考虑冠层和植被对降水的截留作用,这会使模拟过程中的下渗量大于实际入渗量,导致土壤含水量模拟值偏高和含水量变化幅度较大的情况;②10 ~ 40 cm处基于PTF计算出的渗透系数可能偏小,导致土壤水储存在中间层,下渗量比实际下渗量少,造成10 ~ 40 cm含水量偏大,而60 cm含水量偏小,图1密云站40 cm和60 cm处的模拟结果也印证了这一点。
大兴站表层(5、10 cm)在模拟的前20天与实际情况拟合度不高,在第10天时土壤含水量增加,但是没有降水,可能是外界灌溉排水等因素造成的,这导致模拟土壤水分运动过程与实际过程存在差异。中间层(20、40 cm)处的模拟结果与实测值相比偏小,尤其是在40 cm处基于所有PTF模拟的土壤含水量均小于实测值,且差值是在所有深度中最大的。究其原因,从表3可得出0 ~ 30 cm的砂粒、粉粒、黏粒的百分比与40 cm处相差不大,但是5、10、20 cm的实际土壤含水量介于0.15 ~ 0.3,而40 cm的含水量却基本稳定在0.3 ~ 0.35,这可能是由于没有精确测量40 cm深度处的实际土壤质地信息(只提供了30 ~ 50 cm深度的信息,表3),或大兴站40 cm处的土壤含水量观测值存在误差。此外,各站点中未提供土壤有机碳含量信息,本文仅基于全球土壤栅格数据库SoilGrids数据集提取出相关信息,可能存在误差,从而导致模拟结果不能很好地与实测含水量相对应。
馆陶站整体上观测土壤含水量随时间变化不如密云站和大兴站强烈,在降水很大的时段实际的土壤含水量增加不多,但是模拟结果却对降水有着很强的响应。例如在30、50 d比较强的降水后土壤应该达到饱和,从图1中馆陶站5 ~ 40 cm的模拟情况可以看出模拟出的饱和含水量与实际的饱和含水量存在较大差异,这可能是由于土壤质地信息存在误差,造成PTF计算出的土壤水力参数产生偏差,从而导致模拟土壤含水量与实测值产生偏差。
2.3 单一PTF的表现与分析
为进一步深入分析各单一PTF预测的土壤水力参数在模拟土壤含水量中的表现,表4列出了不同单一PTF模拟的土壤含水量与观测值之间的RMSE值。表中粗体为同一站点各个深度的最小RMSE值,每个站点在不同的深度表现最好的单一PTF并不完全相同,这说明并不存在普遍优秀的单一PTF。此外,馆陶站中Rawls的RMSE值最低,但经过分析土壤含水量的模拟值与实测值对比图(图1)发现,Rawls并不能很好地刻画土壤含水量的变化,基于Rawls的PTF模拟出的土壤含水量未能反映降水对土壤含水量的影响(如图1馆陶站10 cm、20 cm所示)。馆陶站0 ~ 45 cm黏土含量较高(表3),经对比发现相较于其他PTF,Rawls过低地估计了饱和导水率(s)和形状参数。Vogel等[54]指出在非饱和带模拟中,当接近1时会使模拟结果不容易收敛,产生数值振荡等问题,导致模拟结果与实际情况不符,所以Rawls可能不适用于在黏土含量较高的地区模拟土壤含水量。综合来看并依据总体结果,密云站表现最好的PTF是Rosetta3,大兴站表现最好的PTF是Weynants,馆陶站表现最好的是Rosetta3。

表4 基于不同单一PTF模型模拟的土壤含水量与观测值之间的RMSE
注:表中粗体为同一站点各个深度的最小RMSE值(包含基于BC方程和VG方程构建的PTF);总体结果不是各个深度RMSE的简单平均,而是所有深度的模拟含水量和观测值计算得到的RMSE。
3个站点表现最优的PTF都是以VG方程为基础构建的。从3个站点共计18个深度的RMSE来看,16个深度的最小RMSE都是基于VG方程所构建的PTF得到的,表明基于VG方程构建的PTF在计算土壤水力参数中具有较大的优势,这可能是由于VG方程所描述的土壤水分特征曲线是一条连续曲线,BC方程则对应着分段函数,而实际测量土壤水分特征曲线为一条连续曲线,BC模型在描述土壤水分特征曲线中具有一定的局限性(公式1、2)。
2.4 不同集合PTF模型的表现与分析
与图1基于单一PTF的模拟结果相比,基于集合PTF模型的土壤含水量模拟值(图3)能更好地综合单一PTF的模拟结果,如图3各站点3种集合PTF模型在100 cm处的土壤含水量模拟值与实测值吻合度较高,而单一PTF的模拟结果则呈现出很大的不确定性。因此,在不能确定何种单一PTF模型为最优模型的情况下,使用集合PTF模型可以降低使用单一PTF模拟土壤含水量造成的系统偏差。
为进一步比较各个集合PTF模型的性能,表5列出了3种集合PTF模型及最优单一PTF模型的RMSE结果(馆陶站Rawls模拟结果与实际情况不符,故未将其加入到集合模型中)。其中平均权重法构建过程简单,但由于其没有基于模拟结果与观测值的关系分配权重,在3种集合模型中的RMSE最大,表现最差;而基于贝叶斯平均法根据模拟结果优化权重分配,其RMSE值是3种集合PTF模型中最小的。
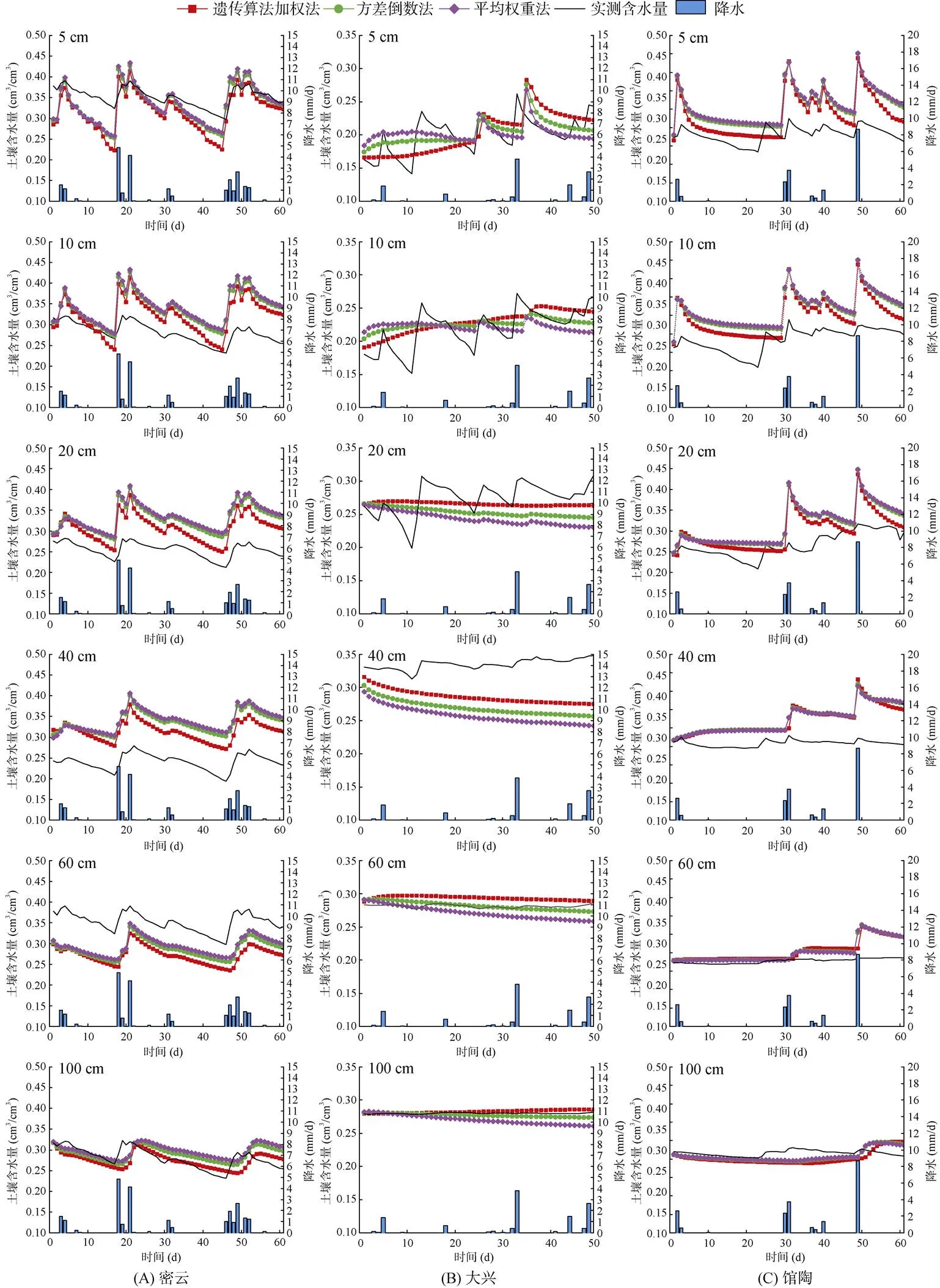
图3 密云站、大兴站、馆陶站基于集合PTF模型模拟的土壤含水量模拟值与实测值随时间变化图

表5 各站点最优单一PTF与3种集合PTF模型的RMSE结果汇总表
注:表中粗体为3个站点各个深度的RMSE最小值;总体结果不是各个深度RMSE的简单平均,而是所有深度的模拟含水量和观测值计算得到的RMSE。
与表现最好的单一PTF比较,3个站点采用贝叶斯平均法构建的集合模型与最优单一PTF的RMSE较为接近。这是因为集合模型综合了所有单一模型的结果,通过捕捉多个单一模型中一致的趋势,减小与实测值相差较大的PTF模型的权重,增加与实测值相差较小的PTF模型的权重来获得更为可靠的模拟结果,避免了对单一模型预测能力的高估和不确定性的低估。
3 讨论
本研究选取海河流域3个通量站,利用广泛使用的7种单一PTF模型提供的土壤水力参数分别运行HYDRUS-1D,并根据模拟结果构建3种集合PTF模型,通过比较土壤含水量模拟值与实测值,评价单一PTF模型及集合PTF模型对土壤含水量模拟结果的影响。
本文中使用土壤有机碳含量作为PTF模型的输入参数,提取自全球栅格数据SoilGrids,以弥补实际采样数据缺少土壤有机碳含量的不足。使用SoilGrids中有机碳含量数据对预测土壤水力参数的预测精度不会有较大影响,主要原因有两点:一是Minasny和McBratney[55]利用60篇公开发表的文献中共约50 000个测量点发现,有机碳含量的变化对于关键水力参数饱和含水量、田间持水量、萎蔫点和有效持水量的影响很小。此外,Zhang等[27]基于全球土壤数据库NCSS将添加有机碳信息与未添加有机碳信息的PTF进行分组研究发现,添加有机质信息与未添加有机质信息的Rosetta3(采用砂土、粉砂、黏土含量的百分比和容重信息为模型输入)模型相比,对模拟结果改善有限,甚至有可能导致模拟结果更差的现象。二是Zhang和Schaap[56]基于全球土壤数据库NCSS中49 855个土壤样品发现,土壤容重和土壤有机碳含量呈负相关关系。当PTF中已将土壤容重作为输入项时,额外增加土壤有机碳含量可能会是重复信息。因此在PTF的输入项中已含有土壤容重时,额外增加土壤有机碳含量对PTF预测土壤水力参数精度的改进有限。
对于单一PTF模型的模拟结果,Rosetta3提供的土壤水力参数在两个站点为最优。这可能是由于Rosetta3模型基于神经网络构建,而其余PTF主要基于回归分析构建,神经网络具有更强的信息处理能力且能更好地模拟复杂非线性关系。另外,构建Rosetta3的数据集覆盖土壤质地类型、容重范围较广,数据较为丰富(表2),而其余PTF数据更集中于某一国家或数据量较少。此外,在本研究中3个站点表现最优的PTF都是基于VG方程构建的。Zhang等[27]利用全球土壤数据NCSS数据库评价了不同单一PTF模型利用土壤基本物理性质预测土壤水力参数,进而对土壤含水量与负压数据点模拟性能的分析。结果表明,基于VG模型构建的PTF的模拟结果优于基于BC模型构建的PTF,Rosetta3、Wosten、Weynants三者PTF的模拟性能最优。本文结果与此一致。此外,Weihermüller等[57]利用13个PTF作为HYDRUS-1D模型运行所需的土壤水力参数,模拟了德国North Rhine-Westphalia地区1982—2011年之间12种土壤质地蒸散量的模拟结果。结果表明:基于利用Rawls模型预测土壤水力参数在运行HYDRUS- 1D时,只有44%的算例可保证收敛,而在所有PTF中Wosten和Rosetta3的模型性能最优,本文所得结果也与此一致。这可能是由于BC方程用分段函数来描述土壤水分特征曲线,而实际土壤水分特征曲线数据是一条连续曲线,VG方程所描述的土壤水分特征曲线更符合实际。目前,在陆面模式等大尺度模拟中大多利用基于BC方程构建的PTF为非饱和带水流运动模型提供水力参数[58],使用基于VG方程构建的PTF提供土壤水力参数有望改善土壤水分运动过程的模拟结果。
在3个站点中大兴站的模拟结果最好(表5),而大兴站土壤质地全为粉壤土,这可能与PTF对粉壤土的土壤水力参数表现更优有关。Wagner等[59]研究结果同样表明PTF对粉壤土的水力参数估计最为准确。
此外,本研究尝试根据土壤含水量模拟结果,使用不同方法对单一PTF赋予权重构建集合模型。结果表明基于贝叶斯平均法构建的集合模型表现最优。这可能是由于贝叶斯平均法通过比较土壤含水量模拟值与观测值的差异,进而优化各个单一PTF的权重分配,使之达到最优。另外,集合模型具有较强的耦合能力,可以将预测因子及函数表达式不同的单一PTF耦合在一起,能够较好地捕捉多个单一PTF预测土壤水力参数以及基于土壤水力参数模拟的土壤含水量的整体趋势,弥补单一PTF在某些情况下模拟误差较大的不足,进而降低单一预测模型所产生的不确定性。
Tebaldi和Knutti[22]指出集合模型优于单一模型的假设为集合模型中的各单一模型相互独立,各单一模型的误差在集合模型中有可能会相互抵消,进而构建的集合模型表现更优,并且随着单一PTF数量的增加,集合模型的不确定性会逐渐降低。在本文中,所选取的各个PTF并非相互独立,如Rosetta3模型使用了部分Weynants、Rawls模型的数据,这可能是集合模型没有显著优于最佳单一模型的原因之一,而可供选择的PTF模型有限,可能是集合模型没有显著优于单一模型的另一个原因。
Hagedorn等[60]指出,虽然在某些情况下,集合模型模拟性能可能不会明显优于单一最优模型,但集合模型在综合性能方面往往有更好的表现。在实际研究中如难以确定最优单一模型,可构建集合模型进而开展模型预测,如在区域、流域等大尺度范围内开展土壤水分运动的模拟研究时,需获取区域、流域等大尺度的土壤水力参数,但往往无法选取出最优的单一PTF模型计算土壤水力参数。故可基于集合PTF模型计算土壤水力参数,弥补单一PTF无法全面解析土壤空间异质性的不足,以及单一PTF存在区域适用性等问题,扩大PTF的适用范围。
本研究中同一站点在各个深度赋予单一PTF的权重相同。然而由于同一站点各个深度的土壤类型不同,土壤含水量也相差较大,在今后的研究中,可基于同一站点不同深度的PTF模型根据土壤含水量实测值与模拟值的结果为不同深度的PTF动态分配权重,有望进一步改善集合模型的模拟结果。
此外,本研究中构建的集合模型为单一PTF赋予统一的权重,在今后的研究中可考虑基于实测土壤水分特征曲线数据,针对PTF预测的土壤水力参数分别设置最优权重,如针对VG方程的r、s、、分别设置最优权重,进而构建出最优的土壤水力参数模型。本研究中选取的PTF均为较常用的PTF模型,在今后的研究中还可以尝试耦合更多的PTF模型,并且可考虑尝试使用更多优化算法构建最优集合模型。
4 结论
1) HYDRUS-1D能较好地模拟3个站点土壤含水量的动态变化,表明7种PTF提供的土壤水力参数在一定程度上均可较好地提供土壤参数化方案。此外,土壤质地、容重、有机质信息等土壤基本性质对于土壤水力参数的预测结果影响较为重要,是准确模拟土壤含水量变化的关键。
2) 在3个站点中表现最好的单一PTF都是以VG方程为基础构建的,说明基于VG方程构建的PTF在预测土壤水力参数方面具有一定的优势。基于VG方程构建的Rosetta3模型所提供的土壤水力参数在3个站点中的两个站点(密云站和馆陶站)表现最优;而Rawls和Weynants模型所提供的土壤水力参数在大兴站点表现最优,RMSE值分别为0.028 6和0.028 7,两者相差不大,但Rawls模型对于黏土含量较高土壤的含水量模拟结果较差,且Rawls模型模拟出的土壤含水量未能反映降水对土壤含水量的影响,故Weynants模型为大兴站最优单一PTF模型。
3) 3种集合PTF模型中,贝叶斯平均法表现最优,而平均权重法表现最差。集合PTF模型预测土壤水力参数可以较好地捕捉多个单一PTF预测土壤水力参数的整体趋势,弥补单一PTF无法全面解译土壤空间异质性的不足,以及单一PTF存在区域适用性等问题,扩大PTF的适用范围。在不能确定何种单一PTF模型为最优模型的情况下,使用集合PTF模型可以降低使用单一PTF模拟土壤含水量造成的系统偏差。
[1] 张英虎, 牛健植, 李娇, 等. 石砾参数对土壤水流和溶质运移影响研究进展[J]. 土壤, 2014, 46(4): 589–598.
[2] 冯徽徽, 刘元波. 2003—2009年鄱阳湖流域土壤水分时空变化特征及影响因素[J]. 长江流域资源与环境, 2015, 24(2): 241–250.
[3] 霍轶珍, 丁春莲, 王文达, 等. 不同封孔方式对番茄缓苗期土壤水盐分布及番茄生长的影响[J]. 土壤, 2020, 52(2): 307–310.
[4] 倪东宁, 李瑞平, 史海滨, 等. 套种模式下不同灌水方式对玉米根系区土壤水盐运移及产量的影响[J]. 土壤, 2015, 47(4): 797–804.
[5] 石文豪, 李奇, 韩琼, 等. 基于不同优化算法的土壤水分特征曲线模型模拟性能分析[J]. 水资源与水工程学报, 2020, 31(4): 157–165.
[6] 黄元仿, 李韵珠. 土壤水力性质的估算——土壤转换函数[J]. 土壤学报, 2002, 39(4): 517–523.
[7] 李文政, 刘目兴, 易军, 等. 三峡山地不同坡位土壤的水分特征曲线及水力学性质[J]. 水土保持学报, 2021, 35(3): 135–142.
[8] 廖凯华, 徐绍辉, 吴吉春, 等. 不同土壤转换函数预测砂土非饱和导水率的对比分析[J]. 水科学进展, 2013, 24(4): 560–567.
[9] 宋杨睿, 王金满, 白中科, 等. 土壤水力特性参数预测方法研究进展[J]. 灌溉排水学报, 2017, 36(S2): 123–128.
[10] 牛晓倩, 贾小旭, 刘成功, 等. 关中平原农田土壤水力参数空间分异与模拟[J]. 水土保持学报, 2021, 35(1): 198–204.
[11] Saxton K E, Rawls W J, Romberger J S, et al. Estimating generalized soil-water characteristics from texture[J]. Soil Science Society of America Journal, 1986, 50(4): 1031–1036.
[12] Schaap M G, Leij F J, van Genuchten M T. Neural network analysis for hierarchical prediction of soil hydraulic properties[J]. Soil Science Society of America Journal, 1998, 62(4): 847–855.
[13] 王来才, 胡海军, 王晨, 等. 不同压实度重塑黄土持水曲线测试及模型预测[J]. 岩土工程学报, 2021, 43(S1): 204–208.
[14] Williams R D, Ahuja L R, Naney J W. Comparison of methods to estimate soil water characteristics from soil texture, bulk density, and limited data[J]. Soil Science, 1992, 153(3): 172–184.
[15] Tietje O, Tapkenhinrichs M. Evaluation of pedo-transfer functions[J]. Soil Science Society of America Journal, 1993, 57(4): 1088–1095.
[16] Kern J S. Evaluation of soil water retention models based on basic soil physical properties[J]. Soil Science Society of America Journal, 1995, 59(4): 1134–1141.
[17] Wösten J H M, Pachepsky Y A, Rawls W J. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics[J]. Journal of Hydrology, 2001, 251(3/4): 123–150.
[18] Dai Y J, Shangguan W, Duan Q Y, et al. Development of a China dataset of soil hydraulic parameters using pedotransfer functions for land surface modeling[J]. Journal of Hydrometeorology, 2013, 14(3): 869–887.
[19] Neuman S P. Maximum likelihood Bayesian averaging of uncertain model predictions[J]. Stochastic Environmental Research and Risk Assessment, 2003, 17(5): 291–305.
[20] Baker L, Ellison D. The wisdom of crowds—Ensembles and modules in environmental modelling[J]. Geoderma, 2008, 147(1/2): 1–7.
[21] 杨栋, 丁烨毅, 金志凤, 等. 浙江水蜜桃成熟期集合预报模型[J]. 中国农业气象, 2018, 39(6): 421–430.
[22] Tebaldi C, Knutti R. The use of the multi-model ensemble in probabilistic climate projections[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 365(1857): 2053–2075.
[23] Guber A K, Pachepsky Y A, van Genuchten M T, et al. Multimodel simulation of water flow in a field soil using pedotransfer functions[J]. Vadose Zone Journal, 2009, 8(1): 1–10.
[24] Raftery A E, Gneiting T, Balabdaoui F, et al. Using Bayesian model averaging to calibrate forecast ensembles[J]. Monthly Weather Review, 2005, 133(5): 1155–1174.
[25] Krishnamurti T N, Kishtawal C M, Zhang Z, et al. Multimodel ensemble forecasts for weather and seasonal climate[J]. Journal of Climate, 2000, 13(23): 4196–4216.
[26] Poeter E, Anderson D. Multimodel ranking and inference in ground water modeling[J]. Ground Water, 2005, 43(4): 597–605.
[27] Zhang Y G, Schaap M G, Wei Z W. Development of hierarchical ensemble model and estimates of soil water retention with global coverage[J]. Geophysical Research Letters, 2020, 47(15): e2020GL088819.
[28] 刘绍民, 徐自为. 海河流域多尺度地表通量与气象要素观测数据集: 密云站—自动气象站(2008—2010)[OL]. 国家青藏高原科学数据中心, 2016, DOI: 10.3972/haihe.001.2013.db. CSTR: 18406.11.haihe.001.2013.db.
[29] 刘绍民, 徐自为. 海河流域多尺度地表通量与气象要素观测数据集: 大兴站—自动气象站(2008—2010)[OL]. 国家青藏高原科学数据中心, 2016, DOI: 10.3972/haihe.004.2013.db. CSTR: 18406.11.haihe.004.2013.db.
[30] 刘绍民, 徐自为. 海河流域多尺度地表通量与气象要素观测数据集: 馆陶站—自动气象站(2008—2010)[OL]. 国家青藏高原科学数据中心, 2016, DOI: 10.3972/haihe. 007.2013.db. CSTR: 18406.11.haihe.007.2013.db.
[31] Liu S M, Xu Z W, Zhu Z L, et al. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China[J]. Journal of Hydrology, 2013, 487: 24–38.
[32] Jia Z Z, Liu S M, Xu Z W, et al. Validation of remotely sensed evapotranspiration over the Hai River Basin, China[J]. Journal of Geophysical Research: Atmospheres, 2012, 117: D13113.
[33] Brooks R H. Hydraulic properties of porous media[M]. 200 W Lake St, Fort Collins: Colorado State University, 1965.
[34] van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892–898.
[35] Clapp R B, Hornberger G M. Empirical equations for some soil hydraulic properties[J]. Water Resources Research, 1978, 14(4): 601–604.
[36] Williams J, Ross P J, Bristow K L. Prediction of the Campbell water retention function from texture, structure, and organic matter[C]//Proceeding of international workshop on indirect methods for estimating the hydraulic properties of unsaturated soil. CA, U.S.A: University of California, Riverside, 1989,
[37] Tomasella J, Hodnett M G. Estimating soil water retention characteristics from limited data in Brazilian Amazonia[J]. Soil Science, 1998, 163(3): 190–202.
[38] Saxton K E, Rawls W J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions[J]. Soil Science Society of America Journal, 2006, 70(5): 1569–1578.
[39] Cosby B J, Hornberger G M, Clapp R B, et al. A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils[J]. Water Resources Research, 1984, 20(6): 682–690.
[40] Campbell G S. A simple method for determining unsaturated conductivity from moisture retention data[J]. Soil Science, 1974, 117(6): 311–314.
[41] Rawls W, Brakensiek D. Prediction of soil water properties for hydrologic modeling[C]. ASCE: Watershed management in the eighties. 1985: 293–299.
[42] Wösten J H M, Lilly A, Nemes A, et al. Development and use of a database of hydraulic properties of European soils[J]. Geoderma, 1999, 90(3/4): 169–185.
[43] Weynants M, Vereecken H, Javaux M. Revisiting vereecken pedotransfer functions: Introducing a closed-form hydraulic model[J]. Vadose Zone Journal, 2009, 8(1): 86–95.
[44] Schaap M G, Leij F J, van Genuchten M T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions[J]. Journal of Hydrology, 2001, 251(3/4): 163–176.
[45] Zhang Y G, Schaap M G. Weighted recalibration of the Rosetta pedotransfer model with improved estimates of hydraulic parameter distributions and summary statistics (Rosetta3)[J]. Journal of Hydrology, 2017, 547: 39–53.
[46] Simunek J, Van Genuchten M T, Sejna M. The HYDRUS- 1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably- saturated media[C]. University of California-Riverside Research Reports, 2005, 3: 1–240.
[47] Šimůnek J, Genuchten M T, Šejna M. Development and applications of the HYDRUS and STANMOD software packages and related codes[J]. Vadose Zone Journal, 2008, 7(2): 587–600.
[48] 范兰, 吕昌河, 王学春, 等. EPIC模型对华北平原冬小麦与夏玉米生长和产量模拟的适用性评价[J]. 麦类作物学报, 2014, 34(12): 1677–1684.
[49] 朱忠礼, 林柳莺, 徐同仁. 海河流域不同下垫面土壤水分动态模拟研究[J]. 地球科学进展, 2012, 27(7): 778–787.
[50] Hengl T, Mendes de Jesus J, Heuvelink G B M, et al. SoilGrids250m: Global gridded soil information based on machine learning[J]. PLoS One, 2017, 12(2): e0169748.
[51] Lambooy A M. Relationship between cation exchange capacity, clay content and water retention of Highveld soils[J]. South African Journal of Plant and Soil, 1984, 1(2): 33–38.
[52] Ajami N K, Duan Q Y, Gao X G, et al. Multimodel combination techniques for analysis of hydrological simulations: Application to distributed model intercomparison project results[J]. Journal of Hydrometeorology, 2006, 7(4): 755–768.
[53] Venables W N, Smith D M. An introduction to R (Vol. 1)[J]. United Kingdom: Network Theory Limited, 2003.
[54] Vogel T, van Genuchten M T, Cislerova M. Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions[J]. Advances in Water Resources, 2000, 24(2): 133–144.
[55] Minasny B, McBratney A B. Limited effect of organic matter on soil available water capacity[J]. European Journal of Soil Science, 2018, 69(1): 39–47.
[56] Zhang Y G, Schaap M. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review[J]. Journal of Hydrology, 2019, 575: 1011–1030.
[57] Weihermüller L, Lehmann P, Herbst M, et al. Choice of pedotransfer functions matters when simulating soil water balance fluxes[J]. Journal of Advances in Modeling Earth Systems, 2021, 13(3): e2020MS002404.
[58] van Looy K, Bouma J, Herbst M, et al. Pedotransfer functions in earth system science: Challenges and perspectives[J]. Reviews of Geophysics, 2017, 55(4): 1199–1256.
[59] Wagner B, Tarnawski V R, Hennings V, et al. Evaluation of pedo-transfer functions for unsaturated soil hydraulic conductivity using an independent data set[J]. Geoderma, 2001, 102(3/4): 275–297.
[60] Hagedorn R, Doblas-Reyes F J, Palmer T N. The rationale behind the success of multi-model ensembles in seasonal forecasting - I. Basic concept[J]. Tellus A: Dynamic Meteorology and Oceanography, 2005, 57(3): 219.
Performance Analysis of Simulating Soil Moisture Content Based on Single and Ensemble Pedotransfer Function
LI Qi1, 2, CHEN Wenjuan1, 2, SHI Wenhao1, 2, SUN Shaobo1, 2, ZHANG Yonggen1, 2*
(1 Institute of Surface-Earth System Science,School of Earth System Science,Tianjin University,Tianjin 300072, China; 2 Tianjin Key Laboratory of Earth Critical Zone Science and Sustainable Development in Bohai Rim,Tianjin 300072, China)
In this study, soil hydraulic parameters estimated by 7 commonly used soil pedotransfer functions (PTFs) were used as the parameters fed into the HYDRUS-1D model, and soil moisture was obtained by solving Richards equation, and was compared with the measured dataset at Miyun, Daxing and Guantao stations in Haihe River Basin. The simulation performance of soil hydraulic parameters estimated by single PTF on the estimated soil moisture was evaluated. In addition, soil hydraulic parameters were also estimated by three newly developed ensemble PTF, and the influence of ensemble PTF models on the simulation performance of soil moisture was evaluated. Results show that RMSE of single PTF model based on van Genuchten equation is the lowest, and the Rosetta3 PTF shows a better performance.The ensemble PTF model developed based on Bayesian averaging model has the best performance in terms of characterizing the overall trend of soil hydraulic parameters estimated by multiple single PTF. In addition, the ensemble model can overcome the deficiency of large error resulted from the single PTF in some cases.
Soil pedotransfer function; Soil hydraulic parameters; HYDRUS-1D; Ensemble model; Bayesian averaging method
S152.7
A
10.13758/j.cnki.tr.2023.03.024
李奇, 陈文娟, 石文豪, 等. 基于单一和集合土壤转换函数模型对土壤含水量的模拟性能分析. 土壤, 2023, 55(3): 658–670.
国家自然科学基金面上项目(42077168)、国家自然科学基金青年项目(41807181)和天津市自然科学基金项目(20JCQNJC01660)资助。
(ygzhang@tju.edu.cn)
李奇(1997—),男,天津人,硕士研究生,主要研究方向为土壤水分运动过程模拟。E-mail: li_qi@tju.edu.cn
