加热炉分数阶PID温度自适应控制系统设计
2023-08-01梁中超郭浩轩
梁中超 郭浩轩


摘 要 针对加热炉温度控制系统控制器参数不易选择的问题,提出一种分数阶自适应PID串级控制方法实现控制器参数自动调整。首先以分数阶PID控制器分别作为温度主控制器和燃气流量控制器,实现加热炉串级温度控制;其次应用自适应理论对控制器进行改进,设计了自适应分数阶PID控制器。最后通过数值仿真,验证了所设计控制系统对加热炉温度控制的有效性和可行性。
关键词 分数阶控制系统 分数阶PID控制 串级控制 加热炉温度控制 自适应控制
中图分类号 TP273 文献标识码 A 文章编号 1000?3932(2023)02?0170?05
加热炉出口温度往往受到燃料气压力、流量波动影响,所以炉口温度控制需要一种稳定性高的控制方法[1]。传统加热炉温度控制多采用PID控制,因其具有结构简单、控制效果好、不需要准确的控制对象模型等特点,至今仍然被用于加热炉控制中[2]。但其控制参数调节比较困难,不同操作人员对各项参数的调整不同,并且容易受到未知现场干扰的影响,直接影响到产品产量[3]。
分数阶微积分是普通整数阶微积分的推广,分数阶控制拓展了PID控制的自由度,能获得更优良的控制性能且具有记忆功能,这种记忆功能确保了加热炉历史信息对现在和未来的影响,有利于改善控制的品质[4]。分数阶微积分与PID控制器相结合,不但具有PID控制的优点,而且由于分数阶算法具有记忆特性,使得控制器可以更好地结合历史数据,提高PID控制能力,增强控制器性能。
加热炉温度分数阶PID控制中,利用PID控制方法成熟且应用广泛的优势[5],进行分数阶控制改进,使得加热炉温度控制更加稳定。但分数阶PID控制效果取决于比例、微分、积分参数的整定和优化,参数的选择直接影响系统的控制速度和稳定性[6]。常规PID参数整定多依靠实际经验,这种方法很难兼顾系统中的各种指标,很难达到最优控制效果[7~9]。近年来,研究人员提出了将自适应控制、模糊控制及神经网络控制等方法与经典PID控制相结合的控制方法,可以兼顾两种或多种控制方法的优点,达到良好的控制效果[10]。文献[11]将模糊PID控制方法应用到加热炉温度控制中,控制器具有参数自整定能力,可以实现对非线性时滞加热炉的温度控制。文献[12]应用遗传算法与传统PID相结合的方法,控制器通过遗传算法对PID参数自整定,可以实现对电加热炉温度的稳定控制。将单神经元算法与传统PID相结合设计单神经元PID控制,控制系统通过单神经元得出的参数作为PID控制参数,并将系统的误差变量作为神经元输入,从而实现对PID参数的调节,该控制方法运算简单,更利于应用到加热炉温度的控制上。文献[13]中,作者应用自适应控制器实现了加热炉各段温度的设定,有效地利用了自适应算法自动调整的能力,完成相关工业生产的优化。文献[14]应用自适应PID控制器实现了加热炉稳定控制,有效地提升了加热炉温度控制的抗干扰能力。从上述研究中可以看出自适应算法具有很好的调节能力,同时PID控制算法可以通过其他算法进行有效调节。自适应PID控制方法较其他调节方法结构更简单且更容易实现,但自适应分数阶PID算法在加热炉温度控制中研究较少。笔者利用自适应分数阶PID控制器的控制特点,通过设计串级控制器实现加热炉的温度控制。
1 加热炉串级温控系统
加热炉温度控制系统可分为燃气流量被控系统与温度被控系统两部分,通过控制燃气流量实现加热炉出口温度的控制,由于燃气流量对炉出口温度的影响具有滞后的特点,故温度被控系统中含有时滞项。
为实现加热炉温度串级控制,分别设计分数阶PID控制器实现流量系统控制和温度系统控制,串级控制系统框图如图1所示。
加热炉出口温度给定值r与检测的实际温度
y相比较后的温度偏差e作为温度控制器的输入。考虑系统具有干扰和时滞,温度控制器采用具有较强鲁棒性的分数阶PID控制器,温度控制器输出u作为流量给定值,流量给定值与流量输出y的误差e作为流量控制器的输入。流量控制系统采用分数阶PI控制器,控制器输出u作用于燃气的調节阀,流量系统中含有扰动,f为流量系统未知扰动。通过燃气阀的改变调整燃气流量,从而调整加热炉出口温度。
2 分数阶串级控制系统设计
2.1 温度主系统控制器设计
首先结合分数阶控制理论,设计分数阶PID控制器对两系统进行控制,分数阶PID控制器为:
其中,K、K、K分别为控制器的比例增益、积分常数和微分常数,可以通过改变控制器中的参数影响控制器的输出,从而实现对被控对象的控制;λ、μ分别为积分阶次和微分阶次,由于控制器含有分数阶微积分,其控制效果更加容易调节且控制效果更好。
温度系统误差e(t)=r(t)-y(t),将温度系统误差作为温度分数阶PID控制器的输入,如图2所示。
通过上述设计可以得出温度串级控制系统中的主控制器,实现加热炉温度主系统的稳定控制,但流量控制未考虑在其中。
2.2 流量副系统控制器设计
考虑到加热炉燃气流量、压力等因素的波动,为实现流量控制系统精准控制,设计分数阶PI控制器对加热炉流量系统进行控制,控制器为:
则分数阶PI控制输出作为温度控制器的控制目标。加热炉燃气流量控制系统设定值r(t)由温度控制器输出u(t)给定,即:
由于加热炉燃气流量受到多种因素干扰,结合流量系统传递函数,系统可表示为:
其中,A、B为流量系统的参数;y(t)为系统流量;f(t)为流量系统未知扰动;u(t)为流量系统控制输出。
流量系统误差e2(t)=u1(t)-y2(t),将流量系统误差作为流量分数阶PI控制器的输入,如图3所示。
上述串级控制方法可以有效地实现加热炉温度控制,减小流量系统未知干扰的影响。但温度控制器中控制参数选取较为困难。为简化温度控制器中参数的选取,并取得更好的温度控制效果,可以将自适应分数阶PID控制应用到加热炉温度控制中,控制器设计方法如下。
3 自适应分数阶PID控制系统设计
结合自适应控制理论,對加热炉控制中的温度控制器G(s)进行改进,设计自适应分数阶PID控制器对温度系统进行控制,自适应分数阶PID控制器为:
自适应函数中3个控制参数的变化直接受到温度系统误差的影响。当加热炉温度与设定温度差别较大时,即温度系统误差e(t)较大时,控制参数调节变快。温度系统误差趋于稳定时,即温度误差e(t)趋近于0,则控制参数变化率也趋近于0,从而实现了分数阶PID控制器参数的自动调节。
考虑到控制器3个参数的调节效果和性能不同,在自适应函数中添加分数阶微分和积分形式。控制器比例系数K随误差大小变化而变化,积分系数K变化与误差积分变化相关,微分系数K变化与误差变化率有关。同时,分数阶PID的3个控制参数还与温度系统误差相关,系统误差为0时,控制器参数停止调节。还可以通过自适应函数中的调节系数ρ、ρ、ρ影响控制参数调节能力。
自适应函数的加入使得分数阶PID控制参数具有自动调节的特点。由于控制参数KP、KI、KD中采用了分数阶算法,使得温度控制器输出u(t)参数取值不仅与上一时刻状态变量有关,而且与系统的历史时间内的状态产生了关联。此自适应函数考虑了被控系统控制时间上的整体性,体现了分数阶具有记忆的特性,可以更好地调节分数阶PID控制参数,实现加热炉温度控制。
4 仿真实验与结果分析
为验证所设计串级控制方法对加热炉温度控制系统的适用性,利用MATLAB对温度系统(1)、(2)进行数值仿真,为更符合加热炉温度特性和流量特性,系统参数选取为K=3,T=852,K=5,T=4,流量系统中含有扰动f=10sin t。为更好地符合实际工程控制的要求,令系统设定温度r(t)=130,在1 s后加入系统。
4.1 分数阶PID控制器仿真
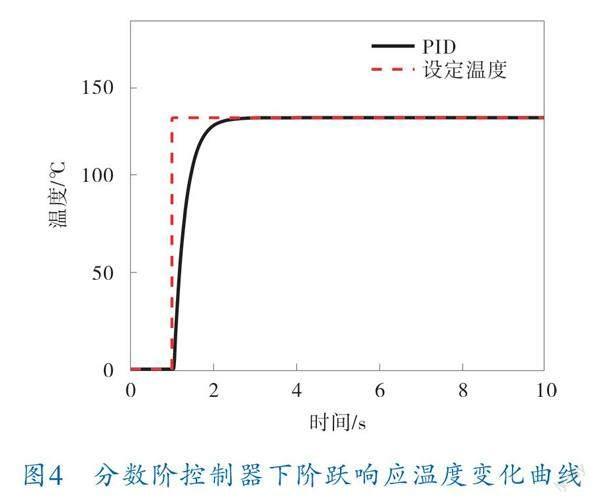
针对以上流量温度串级控制系统,应用设计的分数阶PID控制实现加热炉温度控制。对于温度系统控制器u(t),分数阶中控制器比例、微分、积分参数分别为K=100,K=1,K=0.1。分数阶阶次λ=0.9,μ=0.1。对于流量系统控制器u(t),使用试凑法选取控制参数,流量控制器参数分别为K=10,K=1。对系统进行仿真,仿真效果如图4所示。
从图4中可以看出所设计的串级控制器能够满足加热炉的温度控制,在3 s左右实际温度逐渐趋近设定温度。虽然系统含有扰动,所设计分数阶PID串级控制器仍满足加热炉稳定控制要求。
4.2 自适应分数阶PID控制器仿真
为简化分数阶控制参数调节,适应加热炉多变的控制环境,增强加热炉温度控制系统的控制效果,将串级控制的分数阶PID控制器改进为自适应分数阶PID控制器。选取温度系统控制器
u(t)如式(6)所示,控制器比例、微分、积分参数由自适应函数式(7)进行调节,其初值分别为
K(0)=0.1,K(0)=0.1,K(0)=0.1。自适应函数调节系数分别为ρ=10,ρ=1,ρ=0.01,分数阶阶次不变。选取流量系统控制器u(t)控制参数不变,对系统进行仿真,仿真效果如图5所示。
在加热炉温度串级控制系统仿真中,为更好地对比两种控制器的控制效果,除自适应参数外的其他控制参数与结构均相同,控制系统和设定温度也相同。从图5中可以看出,在自适应分数阶PID控制器作用下,加热炉系统具有更短的稳定时间。
4.3 设定温度改变仿真
为满足工艺产量调节和其他加热炉应用要求,加热炉设定温度会有所调整。为验证控制效果,扩大了温度调整范围,前5 s设定温度为130 ℃,后5 s设定温度为150 ℃。
在所设计控制器下,多设定温度的加热炉变化曲线如图6所示,可以看出两种控制方法都可以满足温度变化调节,自适应分数阶PID控制器温度曲线响应速度更快。
通过上述仿真可以看出,自适应分数阶PID控制器不但适用于加热炉,同样适用于其他多设定值系统的控制。
5 结束语
采用分数阶PID串级控制器实现对加热炉的控制,并应用自适应理论对控制器进行改进,达到了较好的效果。通过仿真对比验证了自适应与非自适应两种串级控制方法,控制器不需要提前求出比例、积分、微分系数,使得控制器搭建更加简单、方便,而且容易转换到其他系统控制中。将分数阶控制方法应用于控制器设计中,提高了控制器的控制速度。由于设计的自适应分数阶串级PID控制器是在温度控制和PID控制基础上改进得到的,因此所设计控制器更容易应用到现有的加热炉温度控制系统中,该方法在实际加热炉系统中将具有较好的应用前景。
参 考 文 献
[1] RAHMANIAN N,AQAR D Y,DAINURE M F,et al.Process simulation and assessment of crude oil stabilization unit[J].Asia?Pacific Journal of Chemical Engineering,2018,13(4):e2219.
[2] 熊昌炯,王春荣,夏尔冬.基于改进PID算法的加热炉温度控制研究[J].中国设备工程,2022(12):101-102.
[3] DEQUAN S H I,GUILI G A O,ZHIWEI G A O,et al. Application of expert fuzzy PID method for temperat?ure control of heating furnace[J].Procedia Enginee?ring, 2012, 29:257-261.
[4] BESCHI M,PADULA F,VISIOLI A, et al. Fractional robust PID control of a solar furnace[J].Control Engineering Practice,2016,56:190-199.
[5] JUNG J,LEU V Q,DO T D, et al. Adaptive PID speed control design for permanent magnet synchron?ous motor drives[J].IEEE Transactions on Power Electronics,2015,30(2):900-908.
[6] 薛美盛,孟俊,刘波.一种基于模型切换的加热炉炉温广义预测控制器设计方法[J].化工自动化及仪表,2017,44(4):347-350;361.
[7] 古训,郑亚利,陈雨青.四旋翼飞行器自适应滑模控制设计[J].控制工程,2020,27(1):138-142.
[8] FOMIN A V,GLUSHCHENKO A I.Improving the control of the OEMK heating furnaces by using param?eter?scheduled adaptive PI controllers[J]. Metallur?gist,2019,63(3):257-263.
[9] 申超群,杨静.温室温度控制系统的RBF神经网络PID控制[J].控制工程,2017,24(2):361-364.
[10] CHERRAT N,BOUBERTAKH H,ARIOUI H,et al. Adaptive Fuzzy PID Control for a Class of Uncertain MIMO Nonlinear Systems with Dead?zone Inputs Nonlinearities[J].Iranian Journal of Science and Technology—Transactions of Electrical Engineering, 2018,42(1):21-39.
[11] SHI D Q,GAO G L,GAO Z W,et al.Application of Expert Fuzzy PID Method for Temperature Control of Heating Furnace[J].Procedia Engineering,2012,29:257-261.
[12] GANI M M,ISLAM M S,ULLAH M A.Optimal PID tuning for controlling the temperature of electric furnace by genetic algorithm[J].SN Applied Scienc?es, 2019,1(8):880.
[13] 陆需飞.一种加热炉温度设定的自适应控制策略[J].冶金自动化,2018,42(1):40-43;53.
[14] 辛星.工业加热炉温度Smith模糊自适应PID控制算法研究[J].中国科技信息,2009(12):52-53.
(收稿日期:2022-09-02,修回日期:2023-03-02)
Design of Adaptive Temperature Control System Based on Fractional Order PID for Heating Furnace
LIANG Zhong?chao1, GUO Hao?xuan2
(1. CHN Energy Yulin Chemical Co., Ltd.;2. School of Electrical Engineering & Information, Northeast Petroleum University )
Abstract Considering the difficulty in choosing controller parameters PID of the heating furnace temperature control system, an adaptive fractional order temperature cascade control for auto?regulation of the controller parameters was proposed. In which, having the fractional order PID controller taken as the main temperature controller and the gas flow controller to realize cascade temperature control of the heating furnace temperature, and then, having the adaptive theory adopted to improve the controller and design an adaptive fractional order PID controller. Numerical simulation verifies both effectiveness and feasibility of the designed control system for the temperature control of the heating furnace.
Key words fractional order control system, fractional order PID control, cascade control, heating furnace temperature control, adaptive control
基金项目:黑龙江省省属高校基本科研业务费项目(2022TSTD?04)。
作者简介:梁中超(1972-),高级工程师,从事转动设备、驱动装置控制系统的研究。
通讯作者:郭浩轩(1989-),讲师,从事自动化控制系统设计工作,a59864963@163.com。
引用本文:梁中超,郭浩轩.加热炉分数阶PID温度自适应控制系统设计[J].化工自动化及仪表,2023,50(2):170-174.
