Fe-Cr-W合金内富Cr团簇形核析出动力学的原子动力学蒙特卡罗模拟

2023-08-01贾丽霞王东杰曹金利豆艳坤贺新福

原子能科学技术 2023年7期

贾丽霞,王东杰,王瑾,曹金利,豆艳坤,吴石,贺新福,杨文

(中国原子能科学研究院反应堆工程技术研究所,北京 102413)

因在350～550 ℃间具有优异的服役性能,低活化铁素体马氏体(reduced activation ferritic/martensitic, RAFM)钢被认为是第四代堆及聚变反应堆候选结构材料之一。低温辐照脆化问题制约其左边服役窗口下限[1]。低活化铁素体马氏体钢以Fe、Cr为主要元素。低温辐照条件下,Fe-Cr合金中形成的纳米级富Cr团簇、位错环等微结构会阻碍位错运动,引发材料硬化、脆化。文献[2]基于分子动力学方法研究了富Cr团簇与位错的相互作用机制及硬化机理,模拟结果发现富Cr团簇会阻碍位错运动,引起剪切应力增大,且剪切应力增加程度与团簇的尺寸、团簇中Cr含量和位错切过团簇的位置均有关。富Cr团簇析出与基体中Cr含量、合金元素、温度、辐照粒子及损伤速率[3]等均相关。如文献[4]表明当基体内Cr含量高于8%(以原子个数计)时,在低温(250 ℃)下进行中子辐照后会形成富Cr团簇;而文献[5-7]表明当Cr含量高于9%(以原子个数计)时才会析出富Cr团簇。由于辐照会增强扩散,富Cr团簇的析出还与温度有关,因为温度会影响空位和间隙的浓度。实验表明,在RPV钢中,合金元素Ni和Mn会影响Cu团簇析出动力学[8-10],从而影响材料性能。在RAFM钢中,W是一种重要的合金元素,它会有效降低RAFM钢中子辐照后韧脆转变温度的增量[11]。W这种效应的微观机理还不清楚,不明确W是否会通过影响富Cr团簇的析出从而影响堆材料性能。本文拟研究Fe-Cr合金中W对富Cr团簇析出行为的影响。

原子动力学蒙特卡罗(atomic kinetic Monte Carlo, AKMC)方法可用来研究团簇析出动力学行为,分析合金元素对团簇析出动力学行为的影响,这得益于它可在模拟体系中处理多种合金元素。文献[12-14]基于AKMC方法,模拟了Mn、Ni等对Cu团簇析出的影响。Bonny等[15]通过团簇展开方法构建了Fe/Cr/W-空位体系的势能,基于AKMC方法研究了Fe-20%Cr-x%W合金在773 K下热老化行为,研究结果表明,W会抑制团簇析出动力学行为。富Cr团簇的析出还与温度、Cr含量等有关。W在不同温度、不同Cr含量下对富Cr团簇析出动力学过程还不清晰。

为研究W在不同温度、不同Cr含量下对富Cr团簇析出行为的影响,本文采用自主开发的原子动力学蒙特卡罗软件研究Fe-Cr-W体系在热老化下团簇析出行为。

1 计算方法

本研究工作利用自主开发的原子动力学蒙特卡罗软件MIET_AKMC(软件著作权号:2019SR0500993)开展。MIET_AKMC可模拟热老化条件下RPV模型合金——Fe-Cu-Mn-Ni合金中团簇析出行为及团簇扩散行为。为开展Fe-Cr合金体系模拟研究,需对原有程序进行升级优化。这是因为原有MIET_AKMC软件主要针对RPV钢中团簇析出行为进行模拟研究,RPV钢为低浓度合金钢(Cu、Mn、Ni含量均小于5%),而Fe-Cr合金为高浓度合金钢(Cr含量高于8%,甚至高达20%)。在初始建模时,应保证Cr原子尽可能在体系内随机化,保证初始构型中不存在小Cr团簇;另外在能量计算时,高浓度合金钢中键能与低浓度合金钢存在差异,在随后阐述中会看到对势中需考虑局域Cr原子浓度的影响,因此需修改对势参数及能量计算部分,使程序可考虑局域浓度相关的对势函数。

热老化条件下体系内缺陷为空位,因此微结构演化是由空位跃迁驱动的。在体系内,空位通过与周围近邻原子发生位置交换,推动微结构发生演化。本软件基于固定晶格点阵模型开发,所有原子均位于BCC晶格点阵上,不存在原子驰豫。空位可与周围8个第一近邻中的任何1个发生位置交换,选择与哪个原子发生位置交换需根据相应的跃迁概率确定。

本软件采用KMC直接法,具体步骤如下:

1) 计算体系内所有事件的概率,即空位向8个第一近邻跃迁的概率ωi(i=1,2,…,8);

2) 记录下所有的概率,在此基础上对所有概率进行累加,得到总概率

(1)

3) 生成随机数rand1;

4) 从总概率表中抽样出满足条件的事件

(2)

即选择ωj事件执行(空位与第j个近邻交换位置);

5) 执行选定的事件后,依据时间暂留算法[16]对模拟时间进行增加

(3)

在KMC模拟过程中,跃迁概率计算非常重要,依据过渡态理论和式(4)获得跃迁概率

ω=ν0exp(-Ea/kBT)

(4)

式中:ν0为尝试频率,本次模拟采用固定值6×1012s-1;kB为玻尔兹曼常数;T为温度;Ea为跃迁激活能,可根据跃迁后、跃迁前体系能量差获得

(5)

(6)

等计算Fe—Cr键能的方法,根据Maximilien Levesque[18]等理论混合能与有序能有下列关系式:

ΔHmix=-Ω(x)x(1-x)

(7)

对混合能进行拟合,可获得有序能Ω(x)。

通过拟合获得Fe—Cr键能的有序能为:

Ω(x)Fe—Cr=(x-0.101 92)(-2.263 63x2+3.922 76x-2.272 55)

(8)

Fe—W键能的有序能为:

Ω(x)Fe—W=(x-0.025 61)(-3.398 88x2+6.453 11x-4.446 83)

(9)

Cr—W键能的有序能为:

Ω(x)Cr—W=(x-2.787 86)(-0.079 65x2+0.136 6x+0.238 06)

(10)

Vac—Vac键能根据下式得到:

(11)

式中,1nn Vac—Vac结合能为0.18 eV,2nn Vac—Vac结合能为0.21 eV。以同样方法可得到Cr—Vac、W—Vac键能,其中Cr—Vac 1nn结合能为0.06 eV,W—Vac 1nn结合能为0.14 eV。最终确定的键能列于表1,表中Θ=1 480 K,表未列出的第二近邻的键能为第一近邻键能的1/2。

表1 模拟所用键能Table 1 Pair-potential for simulation

首先构建了40×40×80的菱形晶体模型,该模型基于BCC-Fe刚性点阵模型,采用周期性边界条件,模拟体系内共128 000个原子。由于刚性点阵模型简单,被广泛用作AKMC方法。刚性点阵模型具有其适用性,主要适用于共格析出相的模拟研究。Fe-Cr合金中析出的α′相、富Cr团簇仍保持BCC点阵,即析出团簇与基体共格,因此Fe-Cr合金中团簇析出仍可采用on-lattice点阵模型。在模拟体系内放置1个空位。按所研究的Cr或W浓度,在体系内随机选择相应数量的Fe原子置换为Cr或W。Cr浓度考虑了8%、10%、16%、20% 4种情况;W浓度考虑了1%和2%两种情况。模拟温度设置为473～973 K,模拟时间设为106蒙特卡罗步。

原子动力学蒙特卡罗模拟时,在体系内放置1个空位,则空位浓度为8×10-6(=1/128 000)。BCC-Fe中空位形成能通常为1.80～2.18 eV[15,17],通常认为空位的平衡浓度与空位形成能及温度存在关系:

(12)

由式(12)可预估出体系内空位的平衡浓度。选取空位形成能为1.9 eV时,473 K时空位平衡浓度为5.93×10-21,973 K时空位平衡浓度为1.47×10-10。这两个温度下空位浓度均远低于模拟时体系内的空位浓度(8×10-6),即原子动力学蒙特卡罗模拟为加速模拟。同时在模拟过程中,尽管模拟体系内仅含1个空位,但由于空位在BCC-Fe中形成能较低,在团簇析出过程中,空位不会被捕获在团簇中而不能自由跃迁,因此,空位会一直在体系内驱动团簇析出。

为得到团簇析出的真实物理时间,需将蒙特卡罗模拟时间转化为真实物理时间,转化公式为:

(13)

式中:tMC为蒙特卡罗模拟时间;CVac,sim=10-6,为模拟体系中空位浓度;CVac,real为真实空位浓度;treal为真实物理时间。CVac,real精确计算较复杂,通常采用简易模型,如式(13)所示。更精确的计算需考虑溶质元素浓度对其影响,如二元体系中可依据下式计算:

(14)

由于本文模拟涉及三元合金,CVac,real准确计算更复杂。而由式(13)可知,蒙特卡罗时间与真实物理时间呈正相关。本文主要目的是分析Cr含量、W含量对富Cr团簇析出影响,选用蒙特卡罗时间作为时间轴,并不影响结果分析,因此本文选用蒙特卡罗时间做时间轴。作者后续将会关注蒙特卡罗时间与真实物理时间的精确转化关系,提高蒙特卡罗模拟时间与真实物理时间转换的准确性。

模拟结束后,依据Bonny等[19]提出的方法对体系内的原子进行团簇分析。首先,计算每个晶格点在其5nn近邻范围内的局域Cr浓度。如果某晶格点的局域Cr浓度高于给定阈值浓度,则该晶格点及其5nn范围内的近邻原子成为1个团簇。这里局域浓度被设置为0.94。

对每个团簇而言,假设其形状为球形,则它的体积可根据原子平均体积乘以原子数计算:

(15)

2 结果和讨论

2.1 软件模拟结果和势函数的验证

图1示出了Fe-20%Cr-x%W在773 K热老化时,富Cr团簇的平均半径和数密度随模拟时间演化关系。通过与Fe-20%Cr合金曲线峰值时间(数密度最高值时对应的时间)进行对比,添加1%W和2%W后曲线峰值时间分别延后50%和150%。这与Bonny等[15]结果一致,其发现加入1%W和2%W后,峰值时间分别延迟40%和150%。同时发现,W的添加并不影响曲线形状和最大数密度,与Bonny等结果一致。模拟的数密度最高值为1×1026m-3,Bonny等计算的最高数密度为4×1025m-3,这可能由于采取了不同的Fe-Cr混合能和有序能,参考Martinez等[17]的数据,本文模拟构建的Fe—Cr键能可考虑局域Cr浓度及温度的影响。

图2示出了模拟开始及结束后Cr和W的原子分布图。从图2可知,模拟结束后,Cr原子形成团簇,而W仍保持固溶态。这也说明团簇的主要成分为Cr。通过分析团簇的成分,发现Fe-20%Cr-2%W体系内形成的团簇中W和Fe的浓度分别为0.3%和5.5%,Fe-20%Cr-1%W体系内团簇中W和Fe的浓度分别为0.1%～0.2%和5%。两个体系内团簇中W浓度的差异是由于基体中初始W浓度不同引起的。体系内约3%的W参与成团析出。

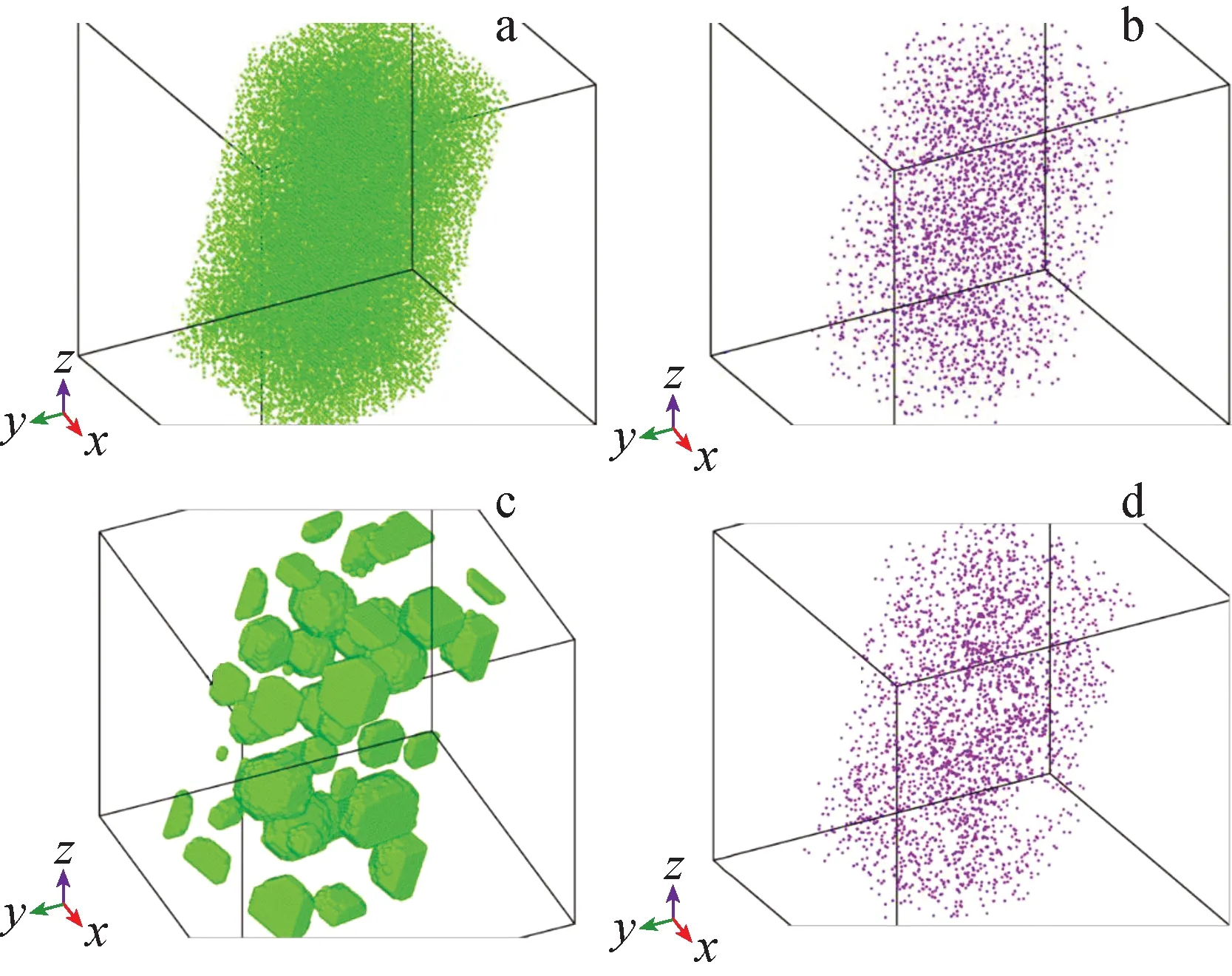
图2 模拟开始时Cr(a)、W(b)以及模拟结束后Cr(c)、W(d)的原子分布图Fig.2 Snapshoot of initial distributions of Cr (a) and W (b) and finial distributions of Cr (c) and W (d)

尽管在本文所研究的时间内,W仍处于固溶态,但它却延迟了析出动力学过程。在拟合对势时,Cr和位于其1nn近邻位置的空位间结合能为0.06 eV,而W与其1nn近邻空位间结合能为0.14 eV。富Cr团簇的析出行为由空位和Cr原子交换驱动。当W和空位间结合能高于Cr与空位结合能时,W与空位结合概率高,会在一定程度上抑制Cr与空位的相互作用,从而会影响富Cr团簇析出动力学行为。

2.2 Fe-y%Cr-x%W合金内富Cr团簇析出动力学行为

对程序进行初步验证后,利用自主软件研究了不同Cr含量(8%、10%、16%、20%)、不同W含量(1%、2%)的Fe-Cr-W体系在不同温度(473～973 K)下的析出动力学过程。

1) Cr含量对富Cr团簇析出动力学行为的影响

图3示出了773 K时不同Cr含量的Fe-Cr合金中析出的富Cr团簇的平均半径、数密度随蒙特卡罗时间演化关系。模拟后所有合金中均形成了富Cr团簇。根据图3中演化曲线形状可知,富Cr团簇的形成经历了均匀形核、长大和开始粗化过程:形核过程表现为团簇的半径和数密度随时间的增加而增加;长大过程表现为团簇的半径持续增加而数密度基本保持不变。经历形核和长大过程后,团簇开始粗化,此时半径仍持续增加而数密度则下降。由于AKMC方法是基于原子与原子的位置交换来实现体系演化的,因此基于AKMC方法的模拟是耗时间的。通常用AKMC方法来模拟团簇析出的形核和长大过程,而采用更高尺度的方法(如团簇动力学、相场)去研究团簇粗化过程。

图3 773 K时不同Cr含量的Fe-Cr合金中析出的富Cr团簇的平均半径(a)、数密度(b)随蒙特卡罗时间演化关系Fig.3 Evolution of average radius (a) and number density (b) of Cr-rich clusters for Fe-Cr alloy with different Cr contents at temperature of 773 K

从图3a可看出,初始形核的团簇平均半径在0.4～0.5 nm之间,与Bonny等[20]发现富Cr团簇形核时稳定籽核的临界半径(0.4～0.6 nm)一致。初始形核临界尺寸与Cr含量无关。通过从图3中提取团簇数密度峰值对应时间(峰值时间)、峰值时间对应的团簇平均半径和数密度得到表2。当处于峰值时间时,团簇的数密度最高,之后会逐渐减少,因此峰值时间处于团簇长大阶段。从表2可知,Fe-20%Cr、Fe-16%Cr、Fe-10%Cr、Fe-8%Cr合金的峰值时间分别为0.002、0.003、0.017、0.020 s。峰值时间随Cr含量的增加而减少。基体内Cr含量的多少是富Cr团簇析出的驱动力。高Cr含量加速富Cr团簇的析出动力学过程。从图3a可看出,高Cr含量体系中,团簇平均半径随时间演化曲线的斜率较大,即团簇尺寸随时间演变较明显。在峰值时间,Fe-8%Cr、Fe-10%Cr、Fe-16%Cr和Fe-20%Cr体系内,团簇的平均半径分别为0.54、0.58、0.57 nm和0.59 nm。峰值时间对应的平均半径(长大阶段临界尺寸)几乎与Cr含量无关。Fe-8%Cr、Fe-10%Cr、Fe-16%Cr和Fe-20%Cr体系内,团簇的数密度约6.38×1025、6.85×1025、1.07×1026、1.10×1026m-3。数密度峰值随Cr含量增加而增加。由于Cr原子倾向于聚集成团,参与团簇析出的Cr原子数随体系内Cr含量增加而增加。体系内Cr含量较高,临界形核尺寸和长大阶段临界尺寸与Cr含量无关时,更多的Cr原子会以更多的、大小基本一致的团簇析出,从而使得Cr团簇数密度较高。当模拟时间为0.4 s时(处于粗化阶段,此时存在小团簇溶解,被大团簇吸收的现象),Fe-20%Cr合金中团簇平均半径约1.3 nm,而其他体系中平均半径均小于1.0 nm;Fe-20%Cr合金中团簇数密度低于其他合金钢。这是因为高Cr合金中团簇数密度高,在粗化阶段被溶解的小团簇数密度也较高,较多的小团簇被大团簇吸收,促进大团簇长大;同时团簇数密度较多时,相邻团簇间距较小,团簇通过互联机制长大的现象也更多,也促进团簇长大,造成总的团簇数密度下降快,粗化阶段斜率下降快。

表2 773 K时不同Cr含量的Fe-Cr合金中团簇数密度峰值对应时间以及对应的团簇平均半径和数密度Table 2 Peak time, radius and number density at peak time for Fe-Cr alloy with different Cr contents at temperature of 773 K

2) 温度对富Cr团簇析出动力学行为的影响

图4示出不同温度下Fe-8%Cr合金内析出的富Cr团簇的平均半径和数密度随模拟时间演化关系。通过从图4中提取团簇数密度峰值对应时间(峰值时间)、峰值时间对应的团簇平均半径和数密度得到表3。563、663、773、973 K峰值时间分别为0.367、0.052、0.024、0.005 s。高温对应更低峰值时间,这表明高温会加速团簇析出动力学过程。由于低温下团簇析出动力学行为较慢,实验上采用高温加速模拟分析团簇析出动力学过程。所有温度下,峰值时间对应的团簇平均半径约0.54 nm。973、773、673、573 K温度下峰值时间对应的数密度分别为6.51×1025、6.38×1025、6.24×1025、5.97×1025m-3。在所有温度下,峰值时间对应的数密度几乎相同。这个结论同样适用于Fe-10%Cr、Fe-16%Cr、Fe-20%Cr。Bonny等[20]发现温度会影响团簇的数密度峰值但不会影响团簇尺寸,发现峰值时间对应的团簇尺寸和数密度与模拟温度无关。温度会通过以下方式影响析出动力学行为:(1) 高温下溶质元素溶解度较高,因此团簇析出动力学驱动力减弱,从而影响析出团簇的数密度;(2) 在形核和长大、粗化阶段,空位扩散能力及空位与溶质元素的结合能是影响析出动力学的关键因素,高温导致更高扩散系数,同时温度会影响团簇结合性能,从而影响团簇的数密度。温度对团簇析出数密度的影响是由上述两种效应共同作用的。本文模拟时采用Enrique等拟合Fe-Cr对势函数,该对势函数与局域环境的Cr浓度和温度有关(表1),Enrique等基于该对势可给出与实验较吻合的扩散系数、Cr在Fe中溶解度。

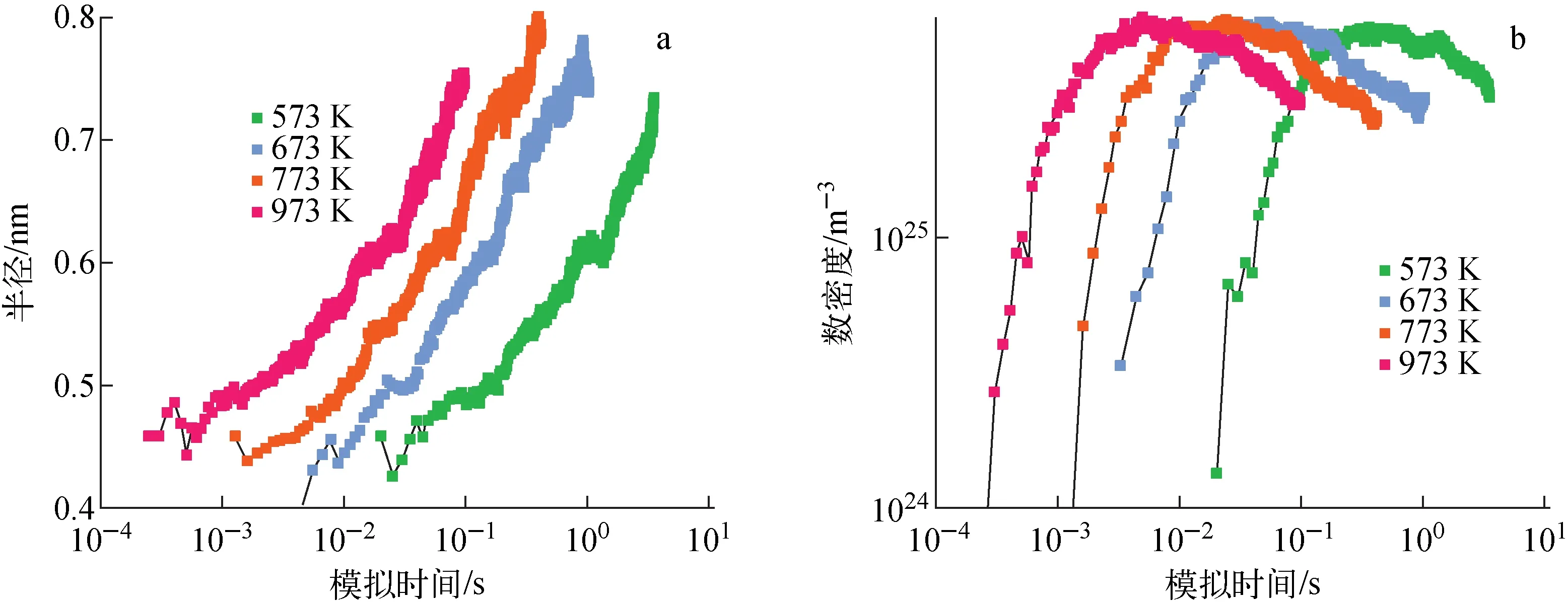
图4 不同温度下Fe-8%Cr合金内析出的富Cr团簇的平均半径(a)和数密度(b)随模拟时间演化关系Fig.4 Evolution of average radius (a) and number density (b) of Cr-rich clusters with simulation time for Fe-8%Cr alloy simulated at different temperatures

表3 不同温度下Fe-8%Cr合金中团簇数密度峰值对应时间以及对应的团簇平均半径和数密度Table 3 Peak time, radius and number density at peak time for Fe-8%Cr alloy simulated at different temperatures

3) W对团簇析出行为的影响

图5呈现了不同温度下,Fe-8%Cr-x%W和Fe-10%Cr-x%W合金内团簇数密度随模拟时间演化关系。可看出,W对沉淀动力学延迟的影响与Cr含量和温度有关。定义W对沉淀动力学延迟程度λ为:

图5 不同温度下Fe-8%Cr-x%W和Fe-10%Cr-x%W合金内团簇数密度随模拟时间演化关系Fig.5 Change of number density with simulation time for Fe-8%Cr-x%W and Fe-10%Cr-x%W at different thermal ageing temperatures

(16)

式中:t0为Fe-Cr体系数密度峰值对应的时间;tx为Fe-Cr-xW体系数密度峰值对应的时间。表4列出了Fe-Cr-W在不同合金成分和不同模拟温度下的延迟程度。图6为不同Cr含量和温度下W的延迟程度。由图6可知,2%的W比1%的W的延迟效应更显著。如前所述,延迟效应是由于W—Vac较Cr—Vac的结合能更高。W含量越高,空位与W结合的概率越高,延迟效应越显著。W引起的延迟效应在较低的温度下更显著。这是因为较高的模拟温度可能引起热振动,从而提高了W—Vac键断裂的概率。温度升高会减弱Cr—Vac、W—Vac结合能的相对强度,从而延迟效应较弱。

图6 不同Cr含量和温度下W的延迟程度Fig.6 Degree of delay by W for different Cr contents and temperatures

表4 Fe-Cr-W在不同合金成分和不同模拟温度下的延迟程度Table 4 Degree of delay by W for Fe-Cr-W with different alloy compositions and different simulation temperatures

从图6可知,当Cr含量为10%时,1%W和2%W的延迟效应最显著。当温度为773 K时,W在Fe-8%Cr和Fe-10%Cr体系中的延迟效应相当。这可用短程有序(short range ordering, SRO)结构的参数解释。SRO参数由Cowley[21-22]提出,用来表征合金的有序度[23-25]。α相中Cr原子第n近邻层的SRO参数可定义为:

(17)

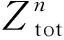
对BCC材料合金而言,第一近邻层和第二近邻层的短程有序参数平均值为:

(18)

它被定义为第一近邻层和第二近邻层的坐标数协调的加权平均值。

Erhart等[23]计算了BCC Fe-Cr中的SRO参数,在模拟温度为100～900 K,Cr浓度为0～16%时,该参数均为负值。这意味着Cr原子倾向于分开,被Fe原子包围,Cr原子不易聚集。SRO参数随Cr浓度增加先减小到最低值再增加。当Cr浓度为8%～12%左右时,SRO参数为最小值;SRO参数最小值对应的Cr浓度与温度有微弱依赖关系。表5呈现了Erhart等计算500～900 K时,Cr含量为8%～12%时的SRO参数。从表中可知,当Cr含量为10%时,SRO参数值最小,短程有序度较高。

表5 Fe-Cr合金的SRO参数Table 5 SRO parameter for Fe-Cr alloy

在BCC-Fe中Cr-Cr相互作用表现为排斥,Cr-Cr排斥作用随着两个Cr原子间距的增加而减弱,当两个Cr原子间距为2.2a0时,相互作用能为0[26]。当Cr浓度为10%左右时,Cr-Cr排斥作用使得该浓度下体系内Cr原子的分布达到饱和状态,因此SRO参数值为最低。随着Cr浓度的增加,使Cr-Cr分离效果最大化的构型组分比例降低,因此SRO参数值增加。BCC-Fe中,Cr-Cr、Cr-W、W-W均表现出排斥作用[27]。BCC-Fe中,当Cr浓度为10%左右时,SRO参数最低,但加入W后,由于Cr-Cr、Cr-W、W-W相互排斥作用,W的加入会引起原子重排布,从而对Fe-10%Cr体系的结构造成较大扰动。原子重排布会影响体系的稳定性,从而影响Cr原子析出动力学过程。

富Cr团簇会阻碍位错的移动,导致材料硬化和脆化[28-32]。Edmondson等研究了FeCrAl体系内α′相的析出,研究发现Al会干扰α′相的析出[33]。Jiang等基于第一性原理计算表明Al和Vac间结合能为0.32 eV[34]。这可能是由于Al与空位间较强的结合能,从而影响了FeCrAl体系内团簇的形核析出行为。目前,Fe-Cr-W体系内团簇析出行为研究较少,本研究结果表明W的加入可延迟富Cr团簇的析出动力学,对材料性能有一定的好处。对因团簇析出而影响服役性能的材料而言,可在其中加入干扰团簇析出的合金元素或结构,从而达到优化材料性能的效果。