NPTS程序质子输运蒙特卡罗模拟方法研究
2023-08-01韩立会张华阳沈华韵
韩立会,张华阳,衷 斌,成 立,沈华韵
(1.北京应用物理与计算数学研究所,北京 100094;2.中国工程物理研究院研究生院,北京 100085)
蒙特卡罗方法已经成为解决不同物理问题的有效方法,在复杂模型粒子输运问题模拟方面具有显著优势[1]。基于蒙特卡罗方法开发的质子输运程序具有广阔的应用前景,例如,在质子束放射治疗中,基于医用辐射剂量体模模拟肝脏质子治疗,得到覆盖整个肿瘤的最佳质子能量区间,并且可以模拟计算出二次辐射传输的中子、光子对患者器官造成的非期望剂量,有助于优化治疗剂量以外的辐射剂量[2];在质子加速器的屏蔽设计方面,蒙特卡罗方法通常被认为是复杂加速器设计分析的最精确方法[3],如应用蒙特卡罗程序模拟优化质子治疗室的屏蔽材料及方案[4]、中子靶物理计算分析[5]、改进束流装置优化质子束性能[6];在太空辐射防护方面,空间辐射环境中占比最高的质子不仅危害飞行机组人员健康,而且会损坏卫星和高空飞行器中的微电子设备,导致严重故障,蒙特卡罗程序可以用来模拟质子在图像传感器中产生的位移损伤,对其在轨安全运行的评估具有重要的研究意义[7]。
国外蒙特卡罗程序发展较早,具备质子输运模拟能力的程序主要包括PHITS[8]、MCNPX[9]、GEANT4[10]、FLUKA[11]等。国内SuperMC采用Bertini核内级联模型开发了质子输运模块,可模拟能量范围至10 GeV[12]。胡志良等开发了一款粒子核内级联蒙特卡罗模拟程序CBIM,可模拟45 MeV以上质子核内级联过程[13]。Zhao等[14]基于INCL核内级联模型与ABLA磨损烧蚀模型在OpenMC上开发了质子中子输运程序IMPC-MC1.0。目前国内具备复杂几何体中质子输运模拟能力的程序较少,且基于核内级联模型、蒸发裂变模型开发的质子输运模拟程序适用的能量范围通常较高,在几十MeV以上。
NPTS程序(neutron-photon transport simulation program)是由北京应用物理与计算数学研究所开发的一款定常中子-光子耦合蒙特卡罗输运程序。本文应用浓缩历史方法基于带电粒子输运连续慢化理论、多重散射理论与能量岐离分布等关键物理模型与ENDF/B-Ⅶ.0核数据库开发质子输运模拟程序,支持1 keV~150 MeV范围内质子的输运模拟计算,实现质子、中子、光子、电子多粒子耦合输运功能,有效拓展NPTS程序在带电粒子输运领域的应用,提高NPTS的应用价值,同时丰富国内中低能质子输运程序的研究方法。
1 质子输运蒙特卡罗模拟方法及物理模型
1.1 浓缩历史方法
描述带电粒子输运的玻尔兹曼方程为:
(1)
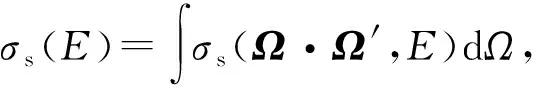
蒙特卡罗方法模拟带电粒子输运计算,最大的问题在于带电粒子的碰撞次数过于频繁。为了减少计算量,Berger提出了浓缩历史的方法[15]。Larsen[16]已证明浓缩历史方法是足够小步长条件下玻尔兹曼输运方程的近似解,本质是人为的解耦了式(1)中的流、角散射和慢化的过程,将位置变化、角度偏转和能量变化3个过程用一种相对简单的蒙特卡罗方法来模拟。
对能量及步长的模拟,程序假设质子每走一步,能量按对数减少:
(2)
式中,K=(1/2)1/m,表示质子每走m步能量损失1/2,m为度量质子游走步长的一个重要参数,当m为6时,每个能量步对应能量损失为10.9%;m为10时,能量损失为6.7%。NPTS支持修改m,快速估算模拟结果时可将m设置稍小些,增加每个步长的能量损失,加快计算速度。
为提高模拟计算精度,在主步之间划分子步,获得更小的子步长,子步的能量间距为:
(3)
式中,ns为根据介质材料划分的子步数量,由经验公式确定。
假设质子沿轨迹的微分能量损失dE/dx是连续变化的函数,对于给定能量损失ΔE的一个质子所走的轨迹步长表示为:
(4)
NPTS应用辛普森积分公式[17]得到与能量损失对应的步长,并通过步长累加得到质子的连续慢化射程。
1.2 带电粒子的能量损失
具有一定动能的质子入射到靶物质中会与原子核及核外电子发生库仑相互作用,发生动量转移与电荷交换,通过连续小能量转移,入射粒子逐渐损失能量,速度变慢。慢化过程中,电子阻止是造成质子能量损失的主要原因,在能量较低(E/A<10 keV)时需要考虑核阻止。
1) 电子阻止
本文应用带有壳层效应修正[18-21]及密度效应修正[22]的Bethe公式计算入射带电粒子的电子阻止,表达形式[23]如下:
(5)
式中:ρ为材料密度;re为电子经典半径;u为原子质量单位,即碳原子重量的1/12;β为相对光速速度;fi为元素的原子组分;Ai为元素的原子质量;Ii为元素的平均电离能;z为入射粒子质量数;m为入射粒子质量;ci为壳层效应修正系数;δ为密度效应校正系数;εmax为质量为m的粒子与一个质量为me的轨道电子(可以认为是自由电子)碰撞过程中可能转移的最大能量:
(6)
由于Bethe公式推导过程中采用一阶玻恩近似,在限制条件β>0.05z2/3范围内准确性较高,对应于质子能量约为1.17 MeV,对于其他重带电粒子如氘粒子、α粒子则分别对应2.34、4.65 MeV[24]。
低能部分程序基于Lindhard理论计算电子阻止,电子阻止公式[25]表示为:
(7)

随着入射质子能量降低速度减小,会从介质原子中获得电子,从而导致入射粒子有效电荷发生改变,使用Barkas经验公式计算有效电荷[27]:
z*=z(1-e-125βz-2/3)
(8)
当质子能量降至NPTS模拟的截止能量1 keV时对应有效电荷为0.087 5个正电荷。
2) 核阻止
对于具有非常小比能量的入射粒子,特别是重带电粒子入射到原子序数较大的靶材料中,由于粒子与靶原子核之间的弹性库仑碰撞导致的粒子减速变得显著。Lindhard等[28]给出了控制这一过程的通用曲线,Steward对该曲线进行最小二乘法拟合得到核阻止计算公式[29]。
(9)

3) 阻止本领计算结果分析
SRIM是一个计算离子在物质中能量损失与射程的程序包,自1985年推出以来被广泛应用[30]。分别使用SRIM程序和NPTS程序计算质子在水、铜、铅3种常见材料中的电子阻止本领与核阻止本领,对比结果如图1所示。能量高于1 MeV时,不同材料与SRIM计算结果的相对偏差在2%以内。当NPTS与SRIM计算结果相对偏差在5%以内时,对应于水、铜、铅的质子能量分别为0.7、0.225、0.250 MeV。

图1 质子在多种材料中的阻止本领Fig.1 Stopping power of proton in different materials
针对验证的3种材料,如图1a所示,NPTS与SRIM在低能段的电子阻止本领偏差较大,特别是对于水材料,Vagena等[31]对GEANT4、MCNP、PHITS、SRIM等程序计算的阻止本领比结果显示,不同程序计算1 MeV质子在水材料中的阻止本领偏差为5%左右,NPTS与SRIM对于入射能量在1 MeV的质子阻止本领偏差为1%。NPTS处理非单质介质的能量损失时基于布拉格相加法则,SRIM阻止本领计算更多考虑了分子结构,在布拉格法则与含有H、C、N、O等元素的化合物之间进行了校正[30]。通过与SRIM结果对比,建议NPTS使用能量范围大于1 MeV,尤其对化合物阻止本领的计算。图1b为核阻止对比结果,因为核阻止只在低能情况下对总的能量损失有贡献,所以本文仅对比1 MeV以下两个程序的核阻止本领的计算结果,3种材料核阻止的计算结果相对偏差均在8%以内,对于铅这种原子序数大的靶材料,核阻止相对偏差在2%以内。
此外同样对比了氘粒子与α粒子在3种材料中总的阻止本领,如图2所示,当总的阻止本领相对偏差控制在5%以内时对应的氘粒子与α粒子能量分别为2.5、5.5 MeV。以上对比结果表明NPTS在较大能量范围内与SRIM吻合较好,可用于计算带电粒子在介质中的平均能量损失以及相应的输运计算。
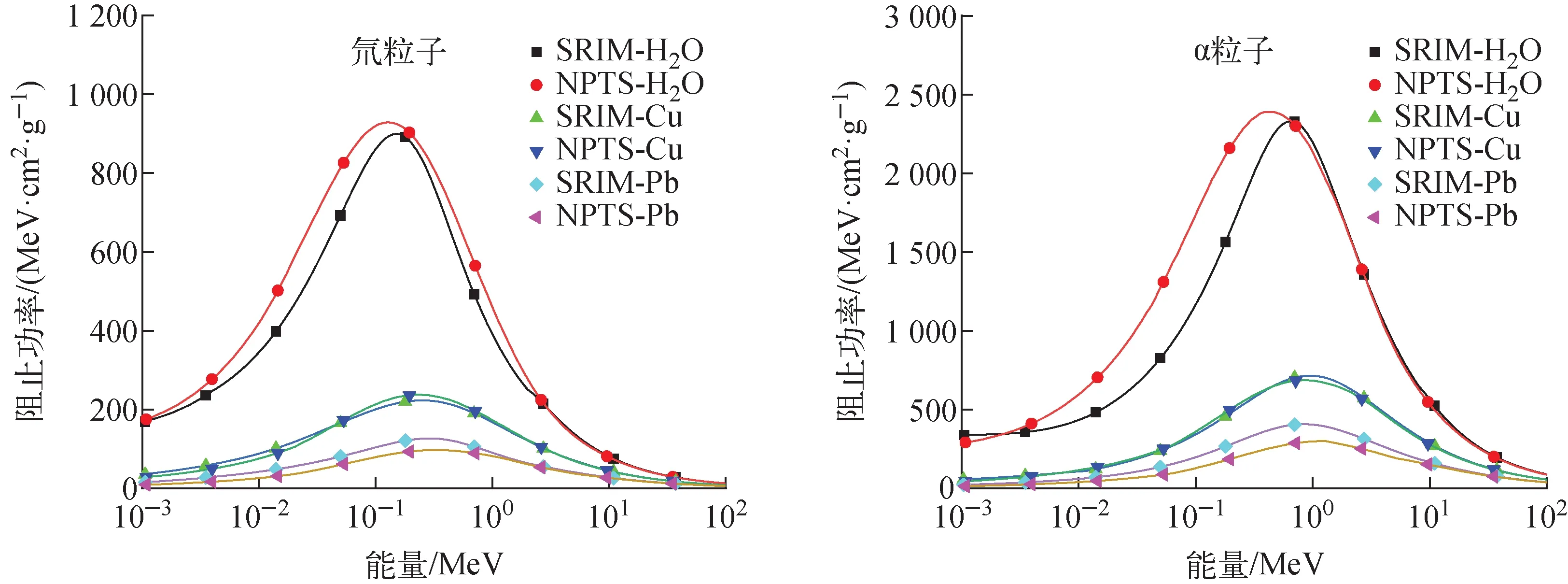
图2 氘粒子、α粒子在多种材料中总的阻止本领Fig.2 Stopping power of D and Alpha particles in different materials
1.3 多重散射
当带电粒子入射到靶物质中时,与原子核及核外电子发生大量的碰撞从而改变粒子的方向,应用多次散射理论得到带电粒子在轨迹末端产生的总偏转角分布。NPTS应用Striganov修正的Molière理论,分布形式如下:
F(θ,t)=
(10)
式中:z为入射粒子质子数;p为动量;N为阿伏伽德罗常数;A为靶核原子质量;参数B、χmax的定义见文献[32]。
Striganov模型和Molière的原始理论之间采用的微分散射截面计算不同,在Molière的理论中,微分散射截面由卢瑟福公式推导得出,带有屏蔽参数:
(11)
(12)
在Striganov模型中,微分散射截面结合粒子与原子核有限尺寸进一步修正得到:
(13)

1.4 能量岐离
电子阻止与核阻止反映了质子在单位距离内的平均能量损失,而每一个能量步代表多次独立的随机碰撞的累积效应。质子在通过同样长度的路程内所损失的能量是不同的,存在一个概率分布,对于质子、氘粒子等重带电粒子应用Vavilov分布描述,形式如下:
(14)
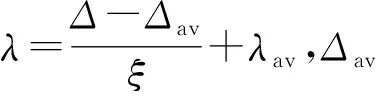
由于Vavilov解析解的复杂性,计算耗时严重,特别是在蒙特卡罗方法模拟带电粒子输运过程,程序中实际应用Rotondi和Montagna开发的近似模型以便快速计算Vavilov分布[34]。该模型根据κ选择适当的拟合函数对Vavilov进行分段拟合。当κ低于0.01时,Vavilov分布近似使用朗道分布描述,对于高于12的κ,近似应用高斯分布。
1.5 质子核数据库
质子核反应采用洛斯阿拉莫斯实验室开发的质子核评价数据库LA150H。LA150H数据评价使用核反应数据计算程序GNASH进行理论分析,并以实验数据为基准,数据为ACE(a compact ENDF)格式[35]。该数据库对重要靶材料和屏蔽同位素的评估延伸至150 MeV,包含41种核素的评价数据。ENDF/B-Ⅶ.0中新增了3H(p,n)、3He(p,n)、6Li(p,n)、7Li(p,n)、9Be(p,n)、10B(p,n)、13C(p,n)的反应数据[36],ENDF/B-Ⅷ.0增加了4He(p,n)反应数据,目前ENDF质子子库包含49个核素的LANL评估数据。质子核数据库支持连续能量中子、光子及带电粒子耦合计算,包含次级轻粒子以及重反冲粒子的产生截面和能量角度分布。NPTS程序基于核数据库精细描述带电粒子核反应及次级中子、伽马及重带电离子的产生过程。
2 程序开发
程序输入文件采用XML语言格式,输入文件以卡片形式书写,主要分栅元卡、曲面卡、材料卡和物理卡四大类,其中物理卡含控制卡、计数卡、加速卡和源卡等描述模型物理相关参数的卡片。开始模拟质子输运前,程序已基于控制卡中模拟质子的能量信息计算并储存了能量网格、平均能量损失、子步长、射程等信息。
单个质子输运过程如图3所示,NPTS模拟步骤如下。

图3 质子输运程序流程图Fig.3 Flow chart of proton transport program
1) 首先进入栅元循环,得到质子所在栅元填充的材料信息,根据经验公式确定内循环子步数。
2) 进入能量循环,根据质子能量与靶材料信息查找步长信息得到子步长ds。
3) 进入最内层子步循环中,通过电子阻止与核阻止计算能量损失,根据损失能量前后的能量平均值查找已处理的截面信息并计算反应距离dr,计算质子到栅元边界的距离db,确认ds、dr、db中最小值为质子输运距离,更新质子位置。根据多重散射理论角分布计算质子偏转角度更新质子方向。根据质子输运距离判断模拟过程,如果db最小,根据边界条件及多重散射偏转角度确认质子是否穿出当前栅元,历史结束或者进入下一个栅元循环;如果dr最小,则基于核数据库进行核反应及次级粒子的模拟;如果ds最小,质子能量网格发生变化且未达到截止能量则更新能量网格索引后重新进入能量循环,反之进入下一次子步循环。
3 结果分析
3.1 中子产额分析计算
应用NPTS程序模拟了不同能量(5、6、7、8、9和10 MeV)质子入射9Be厚靶模型产生的次级中子情况(模拟入射质子数为108,NPTS程序的涨落在0.5%以内),与文献[37]中的GEANT4、MCNP6模拟数据及Atta的实验数据进行对比。中子产额随入射质子能量的变化如图4a所示,不同蒙特卡罗程序模拟得到的中子产额与Atta实验值的相对偏差列于表1。5 MeV时与实验值偏差较大,此时蒙特卡罗程序模拟结果相对偏差均在10%以上,NPTS与GEANT4、MCNP6模拟结果较为一致。图4b为产生的次级中子的平均能量,出射中子的平均能量近似与入射质子能量呈正比,NPTS与GEANT4模拟结果的相对偏差如表1所示,均小于2%。

表1 质子轰击9Be厚靶中子产额Table 1 Thick target neutron yields for 9Be metal

图4 5~10 MeV质子轰击厚9Be靶产生的次级中子信息Fig.4 Neutron information of 5-10 MeV proton bombarding thick 9Be target
BNCT治疗应用的中子能量范围通常在10 keV以下,而出射中子的平均能量与入射质子的能量近似呈正比,在低能情况下锂靶的中子产额、中子出射角度、中子能量方面相比铍靶更适合作为BNCT的靶材料。使用NPTS对能量在7Li(p,n)7Be反应阈值附近的质子入射7Li厚靶模型进行计算(模拟粒子数为109,此时对于不同算例NPTS程序的涨落在0.16%以内)。以Lee等[38]的研究数据为参考,对比NPTS的计算结果,如表2所列。中子产额NPTS的计算结果较Lee等的计算值在1.96 MeV左右最为接近,相对偏差整体在4%以内,出射中子的平均能量与Lee等的数据吻合较好,相对偏差小于1.5%,出射中子平均角度余弦,相比Lee等计算值偏差稍大,但基本在5%以内。

表2 质子轰击7Li厚靶中子产额Table 2 Thick target neutron yields for 7Li metal
应用NPTS程序模拟不同能量质子入射锂、铍厚靶模型,通过与GEANT4、MCNP6及已有研究数据的对比,结果表明NPTS与主流蒙特卡罗模拟程序及实验值具有较好的一致性,验证了NPTS程序在模拟厚靶中子产额方面的正确性。
质子加速器靶的设计过程中需要明确靶的厚度及几何形状,以获得最优的中子束流,应用NPTS测试靶厚对中子产额的影响,计算了不同厚度7Li、9Be靶的中子产额,如图5a、b所示,在一定质子能量下,随着厚度的增加,中子产额曲线会出现饱和,达到稳定,达到稳定的厚度近似等于慢化到产生中子反应阈能的射程,对于锂材料反应阈能为1.88 MeV,铍材料的反应阈能为2.06 MeV。图6为NPTS计算得到的能量在100 MeV以下的质子在7Li、9Be靶当中能量降低到7Li(p,n),9Be(p,n)反应阈能时的射程,根据图6b得到的最佳靶厚与图5a、b程序模拟计算的中子产额最大值时的靶厚非常接近。

图5 中子产额随靶厚度的变化Fig.5 Neutron yields of different thicknesses of target

图6 质子连续慢化射程曲线Fig.6 Proton continuous slowing down approximation range
100 MeV以下质子在7Li、9Be靶中慢化到反应阈能以下的质子射程如图6a所示,根据NPTS给出的图6曲线得到30 MeV质子入射铍靶对应中子产额的最佳厚度为0.6 cm,这与Dorostkar等[39]测试得到的结果相一致。根据图6给出的能量射程曲线可以快速估算出中子产额最大时对应的靶厚,为BNCT靶设计提供有利参考。此外在应用蒙特卡罗程序模拟计算中子产额问题过程中,建议灵活设置质子截止能量,因为低于中子反应阈能的质子对中子产额没有贡献,但计算低能质子输运耗时相当严重,合理设置质子截止能量可以有效地加快计算速度。
3.2 典型质子治疗室辐射场分布
质子治疗通常使用能量70~230 MeV之间的质子束,这个能量范围的质子会产生高能中子、光子和其他带电粒子,其中产生的次级中子在剂量方面占主导地位[40]。典型质子治疗室结构如图7所示[41],内部空间尺寸为6.5 m×6.5 m,高度为3 m,周围的混凝土墙壁厚度为1.5 m,从入口到出口的长度约9.5 m。1束150 MeV的单能质子束从中心沿y轴正方向发射,撞击位于治疗室中心的圆柱形铜靶(直径7 cm,长度7 cm,轴线为y轴),在该区域创建一个辐射场。GEANT4与NPTS计算的质子治疗室中子三维辐射场分布如图8所示,图中,横纵坐标为模拟计算划分的网格数量,对应1个网格xy方向尺寸为5 cm×5 cm。模拟粒子数均为1千万,NPTS治疗室内部通量的平均涨落为0.5%,由于屏蔽墙体计数率低,涨落较大,模型整体平均涨落为7.1%。图8显示两程序铜靶外中子通量分布吻合较好,屏蔽墙体外侧通量计数较低,但从分布形式来看较为一致,验证了NPTS程序在计算复杂几何体中质子、中子辐射场分布的准确性。

图7 典型质子治疗室布置Fig.7 Layout of typical proton treatment room

图8 质子治疗室内中子辐射场分布Fig.8 Neutron radiation field distribution in proton treatment room
4 结论
本文基于NPTS程序,应用带电粒子输运的关键物理模型及ACE格式的核数据库,实现了带电粒子的输运与核反应模拟,开发了适用范围在1 keV~150 MeV的质子输运蒙特卡罗模拟程序,并建立了重带电粒子蒙特卡罗模拟方法与框架。应用NPTS程序对在常见材料中质子、氘核、α粒子的阻止本领与SRIM进行了对比分析,证明了NPTS在计算带电粒子阻止本领方面的正确性。针对厚靶模型得到的中子产额、平均能量、角分布等数值结果与GEANT4、MCNP6及实验结果吻合较好,典型质子治疗室三维辐射场分布与GEANT4一致,验证了NPTS程序质子、中子耦合输运功能的准确性,有效扩展了NPTS程序在质子治疗、加速器设计、屏蔽设计、辐射防护等方面的应用。此外,NPTS程序模拟质子输运应用的物理模型同样适用于其他重带电粒子的输运计算,为进一步研究其他重带电粒子的输运模拟提供了程序基础。
