高低轨共存条件下的卫星通信系统干扰协调技术

邢瑞阳，左增宏，吴启星

（北京跟踪与通信技术研究所，北京 100094）

0 引言

在空天地一体化网络中，某些特殊场景需要对局部范围服务用户扩容或能力增强，可利用不同轨道卫星构成的多层卫星通信网络实现对地面用户的多层覆盖，不同轨道高度的卫星可通过星间链路实现信息交互，从而提高通信资源的利用率。针对低轨卫星作为中继辅助高轨卫星进行信号传输的情况，文献［1］推导了采用放大转发协议下的系统遍历容量。而针对多层卫星通信网络，文献［2］推导了协作非正交多址方案下的遍历容量和中断概率。但是，在实际通信过程中，高低轨卫星会存在同频干扰的问题［3］。因此，在空天地一体化信息网络中，如何通过各种手段来解决网间干扰问题以保证系统正常工作是一个亟待解决的技术问题。文献［4］提出了空天地一体化网络下行链路基于临近空间网络传输速率最大化准则下的功率分配方案。与临近空间平台相比，低轨卫星由于高度更高，所产生的规避区域更大。在高轨卫星与低轨卫星共存的场景下，可以采用认知无线电技术［5］和多色复用技术［6］，从而减小卫星之间的干扰。总的来看，尽管空天地一体化网络的研究正在如火如荼地开展，但目前依然缺乏多层卫星体系架构下系统性能指标的理论分析。因此，本文针对实际工程中可能遇到的天线特性、各种损耗和信道衰落等影响，提出划分低轨卫星规避区域的干扰协调方案，分析了低轨卫星对高轨卫星通信系统干扰产生条件及高轨卫星通信系统中断性能；最后，计算机仿真验证了理论推导的正确性，并评估了低轨卫星位于干扰规避区域之内和之外对高轨卫星通信系统性能的影响，从而为整个网络的规划提供参考。

1 高低轨共存条件下的卫星系统模型

如图1 所示，本文针对一个典型的高低轨共存条件下的卫星通信场景进行研究。

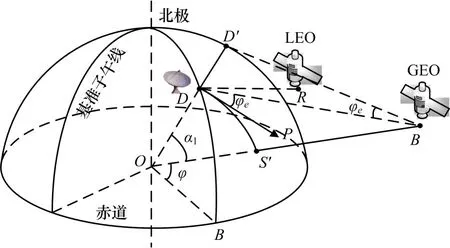
图1 高低轨共存条件下的卫星通信空间几何模型

它由一颗静止轨道通信卫星S，一颗低轨卫星R，以及安装高增益抛物面天线的卫星通信关口站D组成。为了提高频谱效率，高轨卫星通信和低轨卫星通信系统均工作在毫米波频段，并采用相同的工作频率。因此，高轨通信卫星和低轨通信卫星均配置高增益的定向天线，以补偿毫米波自由空间损耗的影响。在这种情况下，卫星通信关口站既接收到需要的高轨卫星信号，又会受到来自低轨卫星的干扰。假设xs(t)和xr(t)分别表示高轨卫星和低轨卫星发射的信号，满足E[|xs(t)|2]=E[|xr(t)|]2=1，式中，E[·]表示数学期望。则关口站接收到的信号可表示为：

式中，hsd和hrd分别表示高轨卫星与关口站，以及低轨卫星与关口站的信道系数；Ps和Pr分别表示高轨卫星和低轨卫星的发射功率；n0(t)是均值为0，方差为σ2=κTB的加性高斯白噪声（AWGN），κ为玻尔兹曼常数，B为噪声带宽，T为噪声温度。在式（1）中，高轨卫星与关口站的信道系数hsd可以表示为：

式中，g1表示小尺度衰落；F1表示路径损耗，其表达式为：

式中，c为光速；f1为工作频率；d1为高轨卫星s到关口站d的距离；Gs表示高轨卫星天线的增益；Gd(φe)表示关口站的天线增益，φe表示高轨卫星距离波束中心的偏移角度，即关口站D对卫星S的俯仰角。根据文献［7］，高轨卫星天线增益Gs可表示为：

式中，Gmax表示高轨卫星最大天线增益；J1(u)和J3(u)分别表示1 阶和3 阶第一类贝塞尔函数，u=2.071 23sinϕv/sinϕ3dB，ϕv表示波束中轴线和接收节点之间的夹角，ϕ3dB表示天线增益衰减3 dB 的角度。根据文献［8］，关口站接收天线增益Gd(φ)可表示为：

式中，Gdmax表示关口站的最大天线增益。

根据文献［9］可知，小尺度衰落g1服从Shadowed-Rician 分布。那么，|g1|2的概率密度函数（PDF）的表达式为：

式中，βl=1 2bl；αl=βl(2bl λl/(2bl λl+Ωl))λl；δl=βlΩl/(2bl λl+Ωl)，参数2bl和Ωl分别表示信道散射分量和直达路径分量的平均功率；λl表示Nakagami-m信道参数；1F1(λl；1；δl x)是合流超几何函数。为了更易分析系统性能，重点关注λl为整数的情况。于是，将1F1(λl；1；δl x)展开可得：

类似地，式（1）中低轨卫星与关口站的信道系数hrd可以表示为：

式中，g2表示小尺度衰落；F2表示路径损耗，其表达式为：

式中，Gr表示低轨卫星天线的增益，根据文献［10］，其dB 形式可以表示为：

式中，Grmax表示低轨卫星天线的最大增益；G(φ)表示水平天线方向图，G(φ)=min {12(φ/φ3dB)，SLL}，SLL 表示低轨卫星天线方向图的旁瓣电平。此外，φ2表示低轨卫星距离关口站波束中心的偏移角度；d2表示低轨卫星到关口站的距离。小尺度衰落g2服从Shadowed-Rician 分布。则|g2|2的PDF 可表示为：

进一步，通过利用公式（1）、（2）和（8）可得到关口站D 的输出信干噪比为：

2 低轨卫星的规避区域

如图1 所示，建立以地心O为球心，以地面站D至球心O的距离re为半径的球面。S为距地面高度为h的高轨卫星，R为距地高度为hr的低轨卫星，S'为高轨卫星S的星下点，关口站D和卫星S的星下点S'的经纬度分别为（φ1，θ1）、（φ2，θ2）。由球面几何理论可知，可以用高轨卫星S的星下点S'来表示高轨卫星S的经纬度。DP为过D指向S'的一条地平线，从而关口站D对高轨卫星S的俯仰角φe表示为∠SDP。

将地心O与关口站D连线延长至DS'点，使得直线SD'平行于直线DP，在直角三角形DD'S中，可以得到：

进一步，可以推算出关口站D对高轨卫星S的俯仰角为：

由图1 可知，为防止对高轨卫星S和关口站D之间的下行通信链路产生干扰，低轨卫星R则应位于关口站接收天线的主瓣波束范围之外，那么规避区域相当于一个顶点在半径为re的球面上，张角为ϕ，与顶点所在水平面仰角为φe的圆锥在半径为ra=re+hr的球面上的截面。为了便于分析，将图1 空间模型的局部取出并重画，如图2（a）所示，关口站D表示圆锥顶点，截面EFHG表示规避区域，其中心点为C。在图2（a）所示的规避区域中，HE是以ra为半径的球面被平面DOS相割得到的球面弧；GF为过OC且与平面DOS垂直的平面OGF与以O为球心、ra为半径的球面相割得到的球面弧。为了精确刻画规避区域的大小，需要求出CE、CH、CF、CG的弧长。

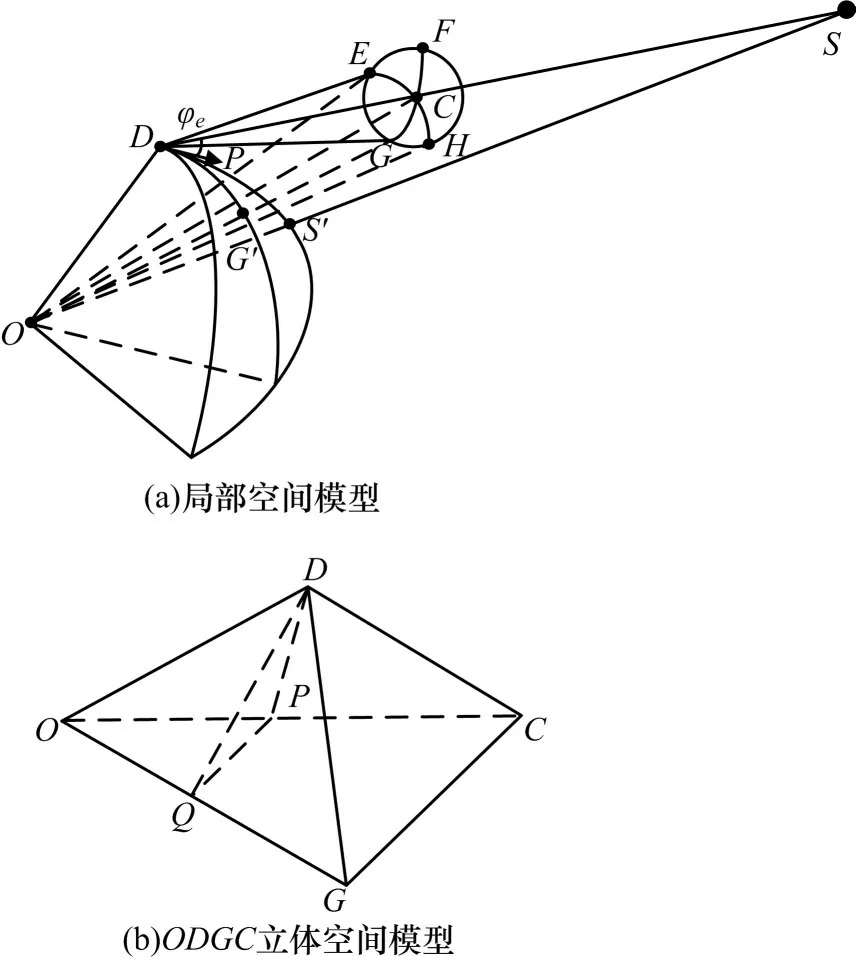
图2 规避区域示意图

首先，为计算出CE的弧长，需要得到弧长CE相对应的圆心角∠COE。在图2（a）中，根据上述条件可知，点D，O，E，H和C在同一个平面内。从而，在CDO中，通过正弦定理，直线OD和直线OC的夹角为：

同理，得出OE与OC的夹角为：

从而得到CE的弧长为a=CE=ra∠COE。与弧长CE的推导方法相似，可得到OH与OC的夹角为∠COH=arccos((racos(φe-ϕ/2)/re))-arccos((racosφe)/re)+ϕ/2，进一步得到CH的弧长为b=CH=ra∠COH。

接下来求解规避区域的弧长CG和CF。首先，作G的星下点G'，DG'为球面上的大圆弧，过D作DG'的切线，该切线必与OG相交，从而点ODCG构成一立体空间，如图2（b）所示。根据规避区域的定义可知，平面OCG垂直于平面ODC，做DP⊥OC，PQ⊥OG，则DQ⊥OG，从而在顶端相接的三个直角三角形（DOQ、DOP、POQ）上，有cos ∠COG=cos ∠DOG/cos ∠DOC。由于OG=OC，从而在DOG中，由余弦定理可知：

同理，在CDG中，可以得到：

而在COG中，由余弦定理可得：

通过联立公式cos ∠COG=cos ∠DOG/cos ∠DOC、以及公式（17）、（18）和（19），可以推导出：

式中，

由于地面接收天线波束主瓣关于地面站和高轨卫星间的连线对称性，所以CG和CF的弧长为：

为了更易分析，将规避区域近似为一个圆面，则C为圆心，最近距离dmin为DC的长度。在DOC中，由正弦定理可以得到DC的长度为：

于是，最近距离dmin的计算公式为：

同理，在DOE中，通过正弦定理可以得出最远距离dmax的计算公式为：

到目前为止，确定了低轨卫星飞行过程中的规避区域，并进一步推导了该区域内到关口站的最近距离dmin和最远距离dmax。

3 高轨卫星通信系统的中断性能分析

基于前面低轨卫星规避区域的计算，本小节在S-D链路和R-D链路的衰落都服从Shadowed-Rician分布的条件下，分析受到低轨卫星干扰的高轨卫星通信系统中断性能。

中断概率是衡量无线通信系统性能的一项重要指标，也可以用来对干扰的效能进行评估。根据文献［15］，OP通常定义为输出信噪比γ小于设定的门限值Λ 的概率，在数学上可以表示为：

式中，Fγ(x)是γ的累积分布函数（CDF）。将公式（12）代入到公式（25），其OP可以进一步表示为：

在S-D链路中，利用公式（6）和公式（12），可以将γsd的PDF 表示为：

利用文献［11］的积分公式，可进一步得到γsd的CDF 为：

在R-D链路中，利用公式（11）和公式（12），可以将γrd的PDF 表示为：

将公式（28）和公式（29）代入公式（26），可以得到中断概率的表达式为：

最 后 ， 根 据 公 式γ(n，x)=(n-1)！(1-和文献［12］的积分公式，系统中断概率可表示为：

需要指出的是，上述推导的中断概率理论表达式（31）适用于不同低轨卫星位置和地面站俯仰角等参数，从而为研究空天地一体化网络的系统性能提供了快速有效的手段。

4 仿真结果与分析

本小节通过计算机仿真来验证理论分析的正确性，同时分析了各种典型参数对系统性能的影响。系统部分参数设置如表1 所示，中断阈值Λ 设为1 dB，考虑高低轨卫星链路经历阴影程度的SR分布为平均阴影衰落（AS）。其中，AS 的信道参数{bl，λl，Ωl}={0.251，5，0.279}。

表1 系统主要参数设置

首先，分析关口站俯仰角对规避区域的影响。图3（a）、图3（b）和图3（c）分别表示长轴和短轴的长度随不同俯仰角φe的变化情况。从图3 中可以看出，低轨卫星的高度越高，长轴和短轴越长，从而规避区域越大，但自由空间损耗导致其需要的功率也越大。另外，根据不同关口站俯仰角的曲线位置可知，关口站俯仰角越低，规避区域越大。因此，可以看出低轨卫星的高度和关口站的俯仰角的大小对规避区域的大小有着很大的影响。

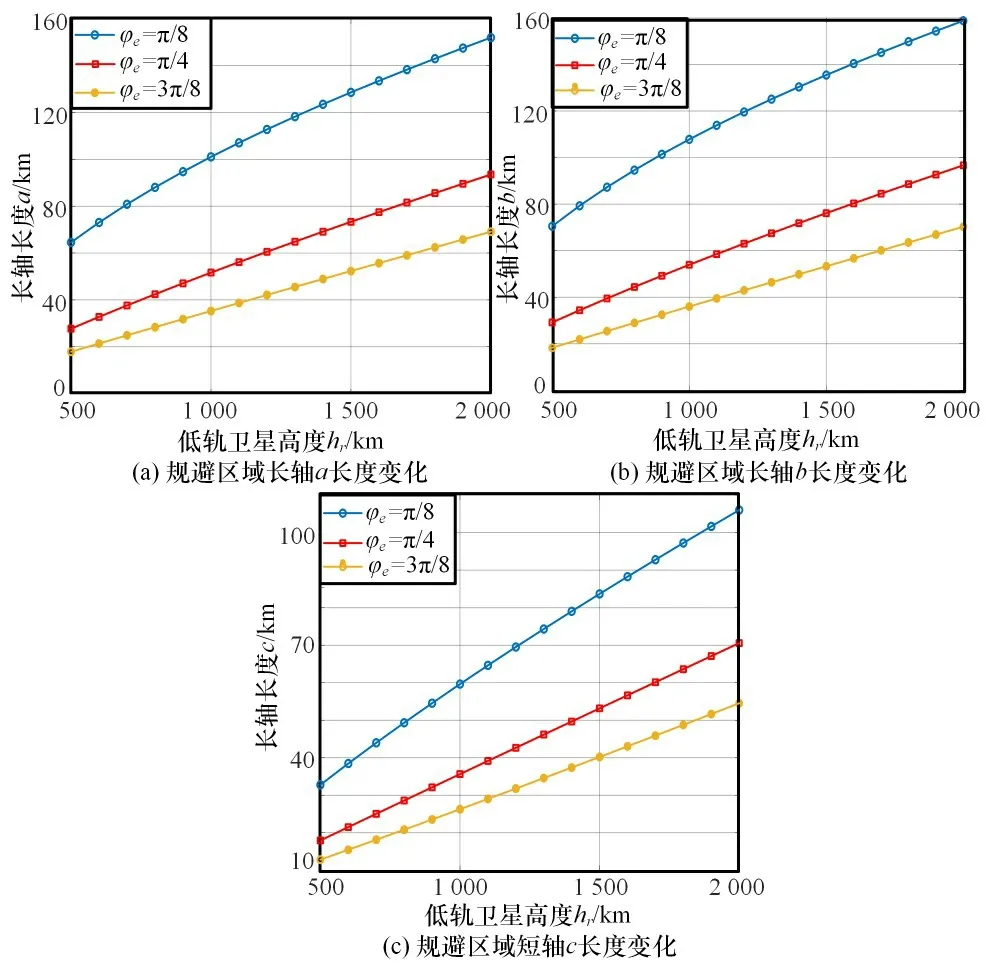
图3 长轴和短轴随不同俯仰角变化情况

其次，分析规避区域对高轨卫星通信系统中断性能的影响。图4 表示了规避区域内到关口站最近距离dmin、最远距离dmax和规避区域外到关口站距离d2下对高轨卫星通信系统中断性能的影响。仿真中，设低轨卫星的发射功率Pr和高度hr分别为20 dBm 和780 km，关口站接收高轨卫星信号时的俯仰角φe为π 8。从图4 中，可以看出蒙特卡罗仿真结果与理论表达式吻合较好，证明了本文对系统OP 理论表达式推导的准确性，并且随着高轨卫星发射功率Ps的增加，中断概率变低。进一步，从图4 中可以看出，低轨卫星处于最近距离时，对关口站的性能影响较大。这是因为低轨卫星距离关口站最近的时候，低轨卫星正处于关口站接收天线的波束主瓣中心，所以对关口站的干扰较大。此外，低轨卫星在规避区域之外，关口站性能明显优于低轨卫星在规避区域内的性能。因此，低轨卫星在飞行过程中应避开这片区域，从而降低对关口站性能的影响。

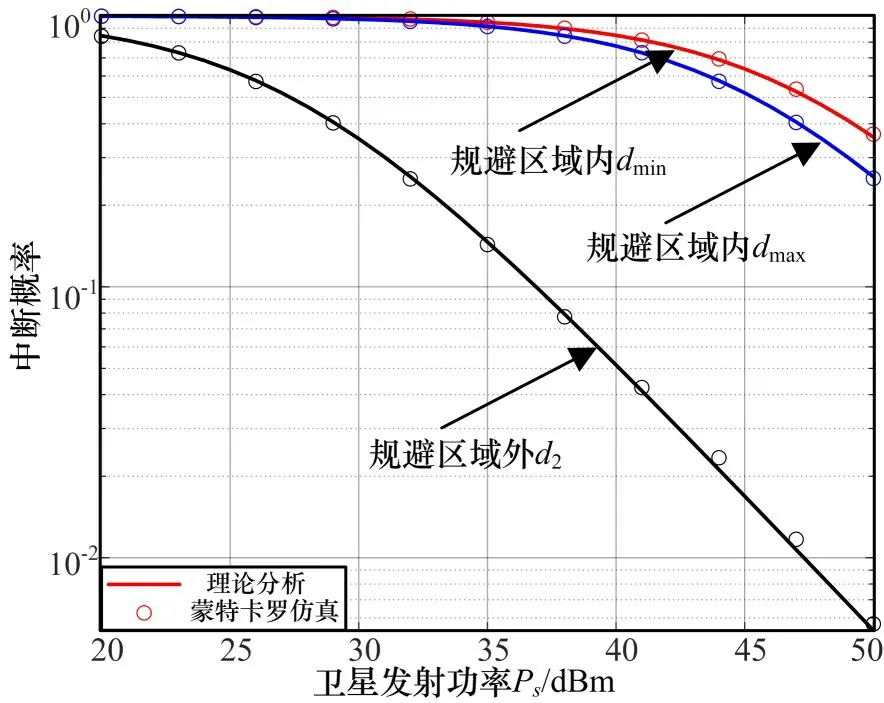
图4 规避区域内距关口站不同距离的系统中断性能

最后，假设高轨卫星发射功率为40 dBm，低轨卫星的发射功率为20 dBm，图5 给出在关口站不同俯仰角情况下的高轨卫星通信系统中断性能。可以看出低轨卫星的高度越高，对关口站的的干扰越弱，高轨卫星通信系统中断性能越好。另外，随着俯仰角的增加，对关口站的干扰强度逐渐增强，高轨卫星通信系统中断性能变差。

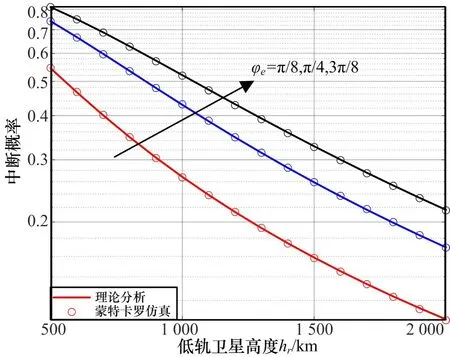
图5 关口站不同俯仰角情况下的系统中断性能

5 结束语

高低轨卫星共存的场景下，为了避免低轨卫星对高轨卫星通信系统的干扰，本文建立了低轨卫星对高轨卫星通信系统的干扰区域模型，分析低轨卫星运行过程中规避区域的约束要求；然后，推导了系统中断概率的闭合表达式，从而为快速评估干扰影响提供了有效手段；最后，通过计算机仿真验证了理论推导的正确性，可为空天一体化网络低轨卫星规划提供约束，对网络体系的构建具有一定参考意义。■