考虑扰动的柔性作业车间多目标动态调度研究
2023-07-31王少参翟书磊
王少参,唐 宇,翟书磊
(1.中国船舶集团有限公司第七一三研究所,郑州 450015;2.南京理工大学 机械工程学院,南京210094)
生产调度是指对具体的生产任务进行决策安排,使得生产任务能够在满足工艺路线、加工设备等实际约束的情况下,达到优化最大完工时间、能耗等生产指标的目标[1]。在数字经济和信息技术的推动下,制造业的生产特征从单品种、大规模的刚性生产逐渐转为多品种、小批量的柔性生产,生产模式的转变让生产过程更加复杂化,同时实际生产中随机出现的扰动事件让生产过程更加难以管控。因此如何有效解决柔性作业车间的生产调度问题(Flexible Job Shop Scheduling,FJSP)成为了学术界的研究热点[2]。
在实际生产的作业车间中,由于产品制造过程繁杂冗长,生产现场的环境因素错综复杂,扰动事件是广泛存在且无法完全消除或避免的。因此针对柔性作业车间的动态调度问题,国内外的专家学者进行了相关研究工作,并取得了一定成果。冯益铭[3]以电子产品复杂精密件为研究对象,对混合柔性作业车间与全自动柔性生产线中的动态调度问题进行了研究,提出了一种带筛选机制的混合驱动方式,建立了包含尾插式调度等3种方法的组合重调度方法;朱旭东[4]以优化最大完工时间为目标,设计了一种基于强制进化遗传算法和记忆优先加工通道的动态调度方法,有效解决了订单加急扰动下的柔性车间动态调度问题;斯兴瑶等[5]为解决柔性车间生产过程中生产效率与设备利用率低下的问题,提出了一种基于滚动窗口技术和遗传算法的柔性车间动态调度方法;张祥等[6]以最大完工时间、设备负载与能耗为优化目标,设计提出了一种多目标柔性作业车间动态调度模型与多目标粒子群遗传算法(Multi-Objec⁃tive Particle Swarm Genetic Algorithm,MOPS⁃GA),能够及时对柔性作业车间中的扰动做出响应;Wang 等[7]为模拟真实的柔性作业车间生产环境,提出了一种包括紧急插单在内共6种扰动的多目标动态调度模型,并设计了一种基于深度强化学习的算法,取得了较好的效果;Li等[8]研究了考虑4种动态事件的柔性作业车间调度问题,设计了一种基于蒙特卡罗树搜索算法(Monte Carlo Tree Search,MCTS)的重调度方法以降低制造跨度,实验证明该方法具有良好的求解质量与计算效率。
NSGA-III算法相比于其他寻优算法具有更好的多样性和全局搜索的能力,因此目前被广泛应用于多目标优化问题的求解中[9]。Liu 等[10]利用NSGA-III 算法对柔性的土方调度问题进行求解,并通过AHP 在Pareto 解集中选取最佳方案以提高效率;安友军等[11]针对多目标柔性作业车间调度问题,设计提出了一种近似支配的NSGA-III-AD算法,有效提高了求解时算法的收敛性、多样性以及局部搜索力度;毕晓君等[12]设计了一种基于参考点约束支配的NSGA-III 算法,以提高算法在求解带约束的高维多目标优化问题时的收敛性与分布性。
为了及时地、有效地应对生产过程中随机出现的扰动事件,本文对车间扰动下的柔性作业车间多目标动态调度问题展开研究。首先确定以重调度需求度为基础的动态调度驱动机制,并给出重调度需求度的度量方法,接着提出以客户满意度、设备总负载以及方案偏移度为优化目标的多目标动态调度模型,并设计一种改进后NSGA-III算法对模型进行计算求解。最后通过实际案例验证该种柔性作业车间动态调度策略的适用性与有效性。
1 基于重调度需求度的混合驱动机制研究
1.1 基于重调度需求度的混合动态调度驱动机制
目前制造行业中应用最为广泛的动态调度驱动机制包括3种:事件驱动机制(Event-Driven Re⁃scheduling,EDR)、周期驱动机制(Periodic Re⁃scheduling,PR)以及混合驱动机制(Hybrid-Driv⁃en Rescheduling,HDR),3 种驱动机制的特点对比结果如表1所示。

表1 动态调度驱动机制对比
本文在考虑柔性作业车间对动态调度实际需求的基础上,结合上述3种动态调度驱动机制的分析,构建完善的动态调度驱动机制。本文考虑在决策是否进行动态调度时,需要综合考虑扰动事件的严重性与生产系统的可调度性。一方面,尽可能地消除扰动事件对生产活动造成的不利影响,另一方面也要避免过于频繁的动态调度操作引起的生产资源的浪费以及生产系统的震荡。
因此,本节在构建混合动态调度驱动机制时引入重调度需求度的概念,表示在综合考虑扰动严重性以及生产系统可调度性的情况下,衡量原定生产计划需要进行动态调度的程度。基于重调度需求度的混合动态调度驱动机制兼顾了显性、隐性扰动对生产车间的影响:对于显性扰动,当扰动出现且重调度需求度大于所设阈值时,则进行动态调度;对于隐性扰动,到达周期调度节点时进行重调度需求度的计算,若需求度大于阈值则触发动态调度。
1.2 重调度需求度度量方法
本文中的重调度需求度为综合性评判指标,需结合生产进度变动率以及加工设备开动率进行确定,各参数的定义以及重调度需求度的具体计算方法如下。
1.2.1 生产进度变动率
将扰动后继续按原调度方案生产的最大完工时间与理想情况下按原调度方案的最大完工时间作对比,将得到的最大完工时间偏移量定义为生产进度变动系数θ。绝对的最大完工时间延迟量不能充分描述扰动对原调度方案的影响程度,因此提出生产进度变动率V的概念,用以表征由扰动造成的生产进度延后对原调度方案的影响程度,由生产进度变动系数与原调度方案最大完工时间T的比值来确定,具体计算公式为:
1.2.2 加工设备开动率
在决策是否需要动态调度之前,需衡量原调度方案的可调度性。本文通过加工设备开动率R表征调度方案的可调度性,可调度性高表明原调度方案加工节奏并不紧凑,设备空闲时间较多。加工设备开动率由原调度方案中加工设备的实际工作时间与最大完工时间的比值确定,计算公式为:
式中,m 为调度方案中的设备数量,Tk为第k台设备的实际加工时长。
1.2.3 重调度需求度
通过综合考虑扰动严重性以及生产系统可调度性,衡量原调度方案需要进行动态调度的程度。重调度需求度S可根据上述两个参数进行确定,计算公式为:
2 考虑车间扰动的柔性作业车间多目标动态调度模型
2.1 问题描述
本文研究的问题可以描述为:优化目标为客户满意度、设备总负载与方案偏移度,调度对象为多个待加工工件,调度结果是为每个工件的每道工序选择合适的加工设备,并安排同一加工设备上各工件的加工顺序,最终达到优化目标的最优化。建立数学模型之前做出以下假设:
1)各个待加工工件优先级相同;
2)工序间转移时间可忽略;
3)各个待加工工件工艺路线唯一;
4)工件完工后入库、发运时间可忽略。
2.2 模型建立
2.2.1 相关参数
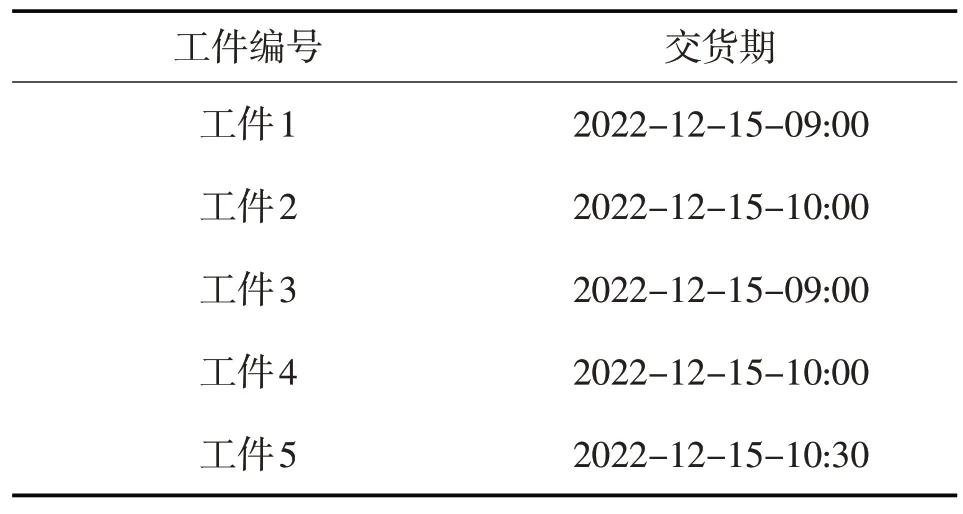
1)待加工工件集合J包含了n个待加工工件,每个工件可表示为ji,每个工件的交货期可以用Di表示,每个工件的完工时间可以用Ei表示(i=1,2,…,n);
2)对于任意一个待加工工件ji,对应的工艺路线为li,li中含有Si个工序,li中的任意工序都可以用Ois(s=1,2,…,Si)表示;
3)作业车间设备的集合为M,总数为m台,每台设备可以记作Mk(k=1,2,…,m);
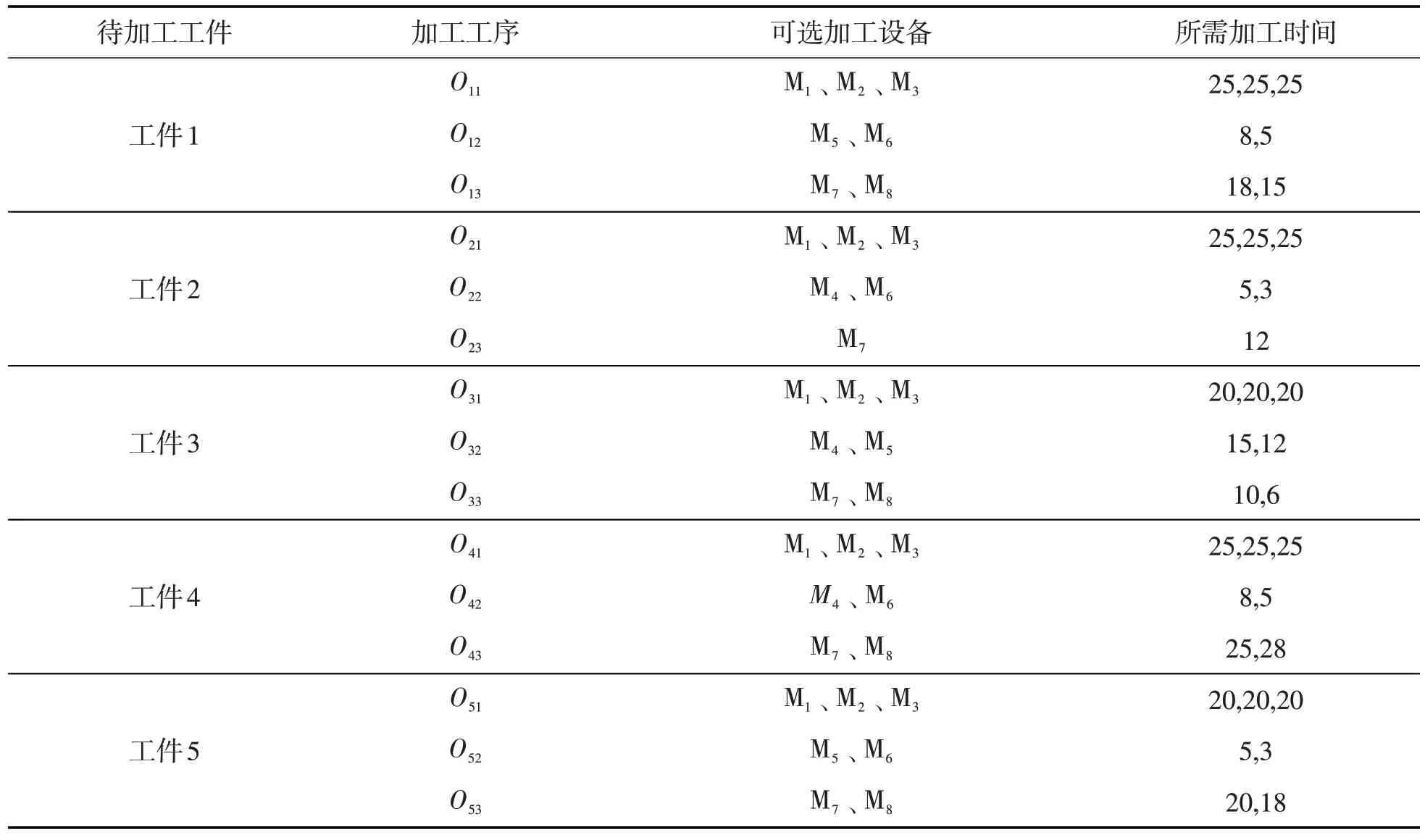
4)对于任意工序Ois,设定至少可以由设备集合M中的一台设备进行加工,由Mis来表示工序Ois可以选择的设备集合;
5)yisk均为{0,1}变量,yisk=1表示工件ji的第s道工序选择了第k台设备,否则yisk=0;
6)tisk表示工件ji的第s道工序在第k台设备上的加工耗时;
2.2.2 目标函数
1)客户满意度
客户满意度一般与订单交付时间有关,订单交付时间越准时客户满意度越高,因此,客户满意度的评价值可通过产品完工时间和交货期的差值确定,且目标函数值越大越优,计算公式如下:
2)设备总负载
本文的设备总负载指标通过所有设备实际工作时长表征,且目标函数值越小越优,计算公式为:
3)方案偏移度
方案偏移度表征动态调度方案相对于原调度方案的优化程度,目标函数值越大越优,可通过客户满意度与设备总负载指标的偏移量进行定义,计算公式为:
式中,α与β取值按实际需求确定。
2.2.3 优化变量
第一个优化变量{0,1}变量yisk,此变量决定了第s道工序的设备选择,设备性能不同导致工序的加工时间会发生变化,进而影响目标函数值。其次,由于动态调度模型中引入了混合驱动机制,所以调度周期Tf、与重调度需求度阈值S0的取值都将影响动态调度模型以及算法的求解,因此将Tf、S0均设置为优化变量。
2.2.4 约束条件
1)设备进行工件加工具有先后顺序:
2)工件加工顺序的正确性:
3)工序加工的完整性:
4)工序对设备的独占性:
5)工序选择设备的唯一性:
6){0,1}变量约束:
对于约束条件1)和2),若同一台设备上需要加工多个待加工工件,本文构建的生产调度模型需要确定该台设备上工件之间的加工顺序,并严格按照加工顺序依次对工件进行加工,前一个工件加工完成后才可进行下一个工件的加工。对于约束条件3)~5),生产调度模型首先确定每个待加工工件的工艺路线,所有工件必须按照相应工艺路线中的工序顺序进行加工,且任意一道加工工序一旦开始,必须等待其完成才可以进行下道工序的加工;每个待加工工件的任意一道工序仅能选择一台可选设备进行加工,且在同一时刻每台设备只能对一个工件的其中一道工序进行加工。对于约束条件6),在本文构建的动态调度模型中,变量yisk与的取值只能为0或者1。
3 求解算法设计
NSGA-III算法的主要机理与NSGA-II算法相似,两者之间的区别在于选择机制的不同。NS⁃GA-III 算法中采用参考点机制代替NSGA-II 中拥挤度排序机制,使得NSGA-III 在高维目标空间内也能保持优异的性能。本文针对实际问题的需要,对标准NSGA-III算法进行设计改进,以最终得到的INSGA-III作为模型求解算法。
3.1 染色体编码
本文提出的柔性作业车间动态调度模型对初始解的质量十分敏感,因此本文采用混沌Logistic映射实数编码方式,提高初始种群在解集空间内分布的均匀度。利用式(13)产生混沌序列:
式中,μ为分叉参数,当3.57<μ≤4 时,Logis⁃tic 映射处于完全混沌状态,本文取μ=4,y0的值由随机函数自动生成。
3.2 交叉算子
采用正态分布交叉算子(NDX)代替原交叉算子,有效提高算法的全局搜索能力,更好地保证解集的多样性,其中,NDX算子的数学表达如式14所示:
式中,P1与P2代表父代种群,Q1与Q2代表子代种群,N(0,1) 为正态分布随机变量,θ为随机数,且取值区间在(0,1) 上均匀分布。
3.3 自适应交叉、变异概率
本文采取自适应交叉、变异概率以提高算法整体性能,保证算法的收敛性与解集的多样性,自适应交叉、变异概率表达式如式(15)和式(16)所示。
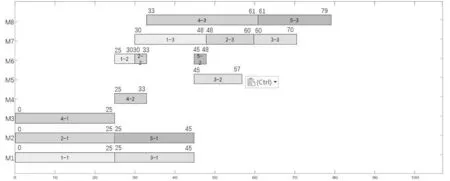
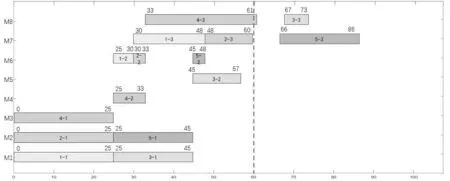
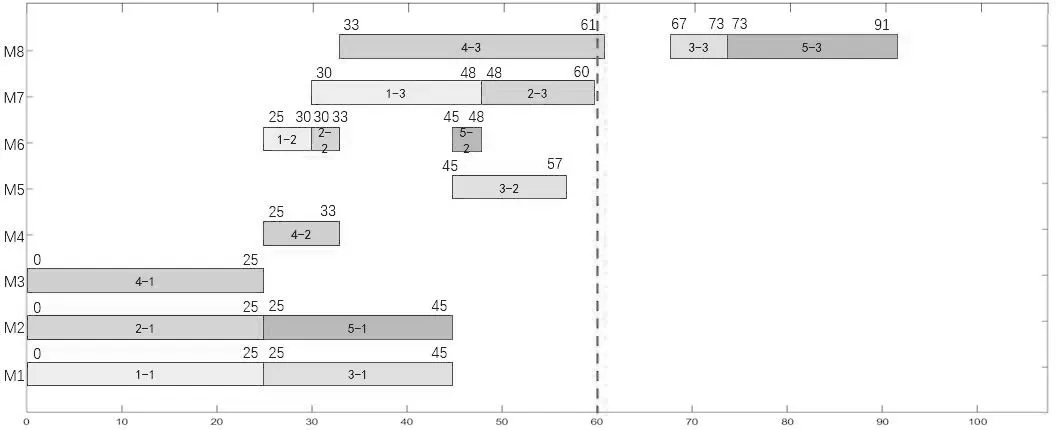
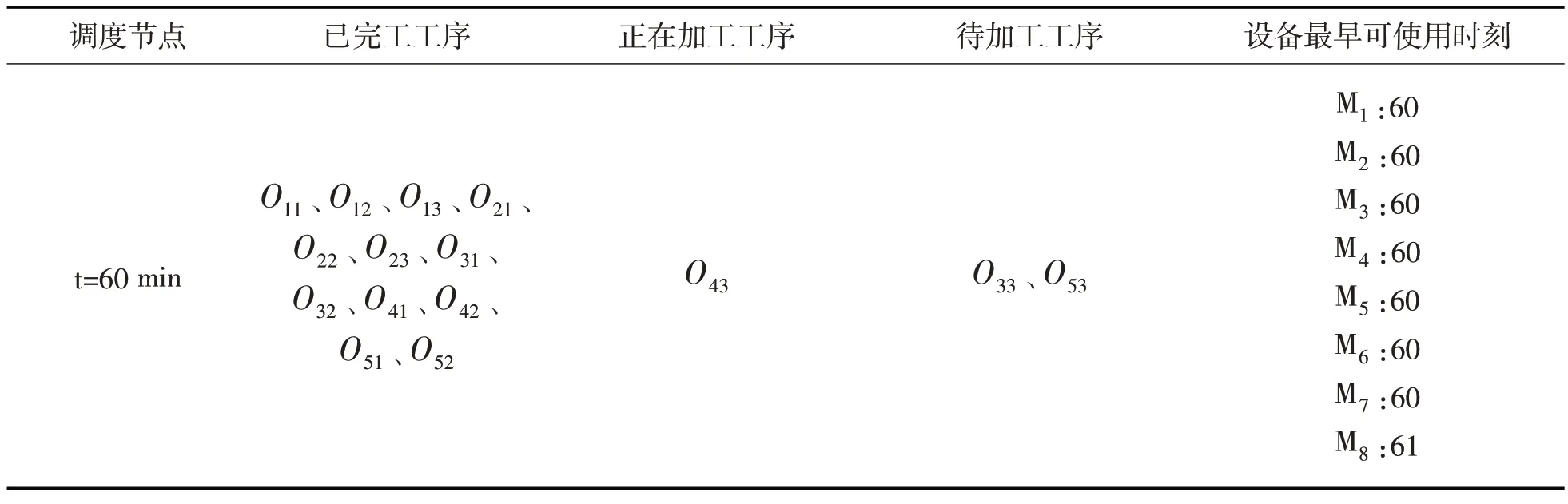
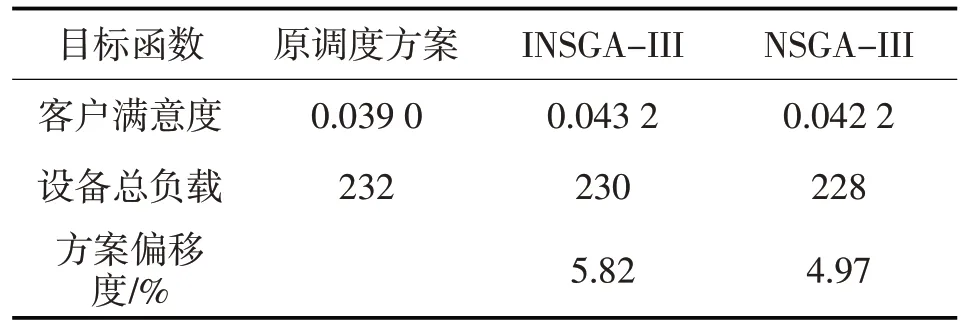
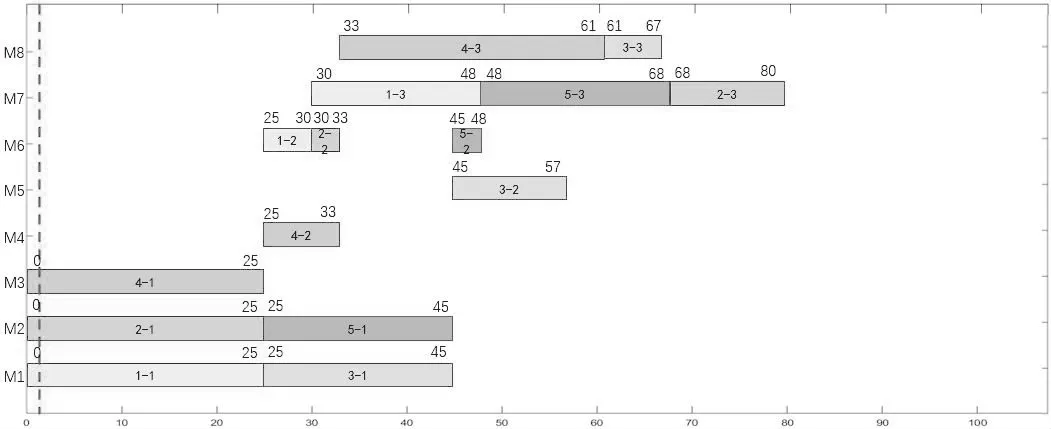
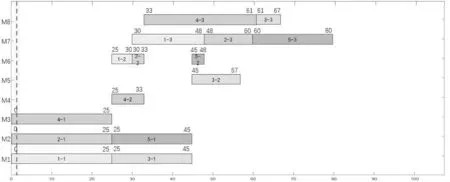
式中,pc为自适应交叉概率,pm为自适应变异概率;fmaxi、fmini与favgi分别为第i个目标函数的适应度的最大值、最小值与平均值;fi表示待交叉个体中较大的适应度值,f'i表示待变异个体的适应度值;k1、k2、k3以及k4均为常数,且0 综合上述分析,整理得到INSGA-III算法流程如图1所示: 图1 INSGA-III算法流程 结合上述混合动态调度驱动机制与INS⁃GA-III 算法的研究,整理得到柔性作业车间的动态调度框架,具体流程如图2所示: 图2 考虑扰动的柔性作业车间动态调度流程 本文选取某企业2022 年12 月15 日上午的加工计划为例,已知当日该企业柔性作业车间内共有5个待加工工件与8台可用加工设备,待加工工件与加工设备的相关信息见表2 和表3,当日初始调度方案甘特图如图3所示。同时,设定本案例中INSGA-III 算法中种群规模为150,最大迭代次数为500 次,α与β均为0.5,调度周期Tf=60 min。为了验证本文INSGA-III 算法的有效性,将NS⁃GA-III作为对比算法,参数设置与INSGA-III保持一致。 图3 初始调度方案 表2 待加工工件信息 表3 工件可选加工设备与加工时间 当t=60 min时,由隐性扰动累积引起的生产进度变动系数为6 min,计算得到重调度必要度大于阈值,执行动态调度操作。整理得到周期调度时刻加工信息如表4所示,根据表4中信息驱动动态调度,由INSGA-III算法求得的动态调度方案的甘特图如图4 所示,由NSGA-III 算法求得的动态调度方案如图5所示。由图4可得,动态调度方案中工序O33于t=67 min时在设备M8上开始加工,工序O53于t=66 min 时在设备M7上开始加工;由图5 可得,工序O33于t=67 min 时在设备M8上开始加工,工序O53于t=73 min时在设备M8上开始加工。 图4 INSGA-III动态调度方案甘特图 图5 NSGA-III动态调度方案甘特图 表4 周期调度时刻加工信息表 由表5 动态调度方案与原调度方案目标函数对比可知,INSGA-III算法求得的动态调度方案相比于原调度方案,客户满意度提高了10.77%,设备总负载降低了0.86%,方案偏移度为5.82%;相比于NSGA-III 算法求得的动态调度方案,客户满意度提高了2.37%,设备总负载升高了0.88%,方案偏移度增大17.10%,虽然设备总负载有所升高,但幅度较低,且客户满意度与方案偏移度均有所提升,因此本文提出的动态调度方法具有较好的应用效果。 表5 周期驱动调度方案目标函数对比 设在t=1 min时刻,工件5的交货期发生变更,由原本的2022 年12 月15 日10:30 变更为同一天08:05,计算得到重调度必要度大于阈值,对生产系统进行动态调度。整理得到显性扰动发生时刻加工信息如表6所示。 表6 显性扰动发生节点加工信息 根据表6 中信息驱动动态调度,由INSGA-III算法求得的动态调度方案的甘特图如图6 所示,由NSGA-III算法求得的动态调度方案的甘特图如图7 所示。由图6 可得,动态调度方案中工序O53于t=48 min时在设备M7上开始加工,工序O23于t=68 min 时开始加工,工序O33于t=61 min 时在设备M8开始加工;由图7可得,动态调度方案中工序O53于t=48 min时在设备M7上开始加工,工序O23于t=68 min 时开始加工,工序O33于t=61 min 时在设备M8开始加工。 图6 INSGA-III动态调度方案甘特图 图7 NSGA-III动态调度方案甘特图 动态调度方案与原调度方案目标函数对比如表7 所示,可知由INSGA-III 算法求得的动态调度方案相比于原调度方案,客户满意度提高了23.21%,设备总负载降低了0.86%,方案偏移度为12.04%;相比于NSGA-III 算法求得的动态调度方案,客户满意度提高了4.03%,设备总负载一致,方案偏移度增大24.77%,虽然设备总负载没有明显优化,但客户满意度与方案偏移度均有所提升,且提升幅度较大,因此本文提出的动态调度方法具有较好的应用效果。 表7 显性扰动驱动调度方案目标函数对比 本文首先结合现有理论研究内容确定了基于重调度需求度的混合动态调度驱动机制,并给出了重调度需求度的计算方法。然后针对柔性作业车间的实际需求,建立了考虑车间扰动的多目标动态调度模型,并设计了一种INSGA-III算法对模型的客户满意度、设备总负载以及方案偏移度3个目标函数进行优化求解。最后分别设置周期驱动以及显性扰动驱动两个案例,验证了本文提出的动态调度驱动机制、动态调度模型以及求解算法的可行性与有效性。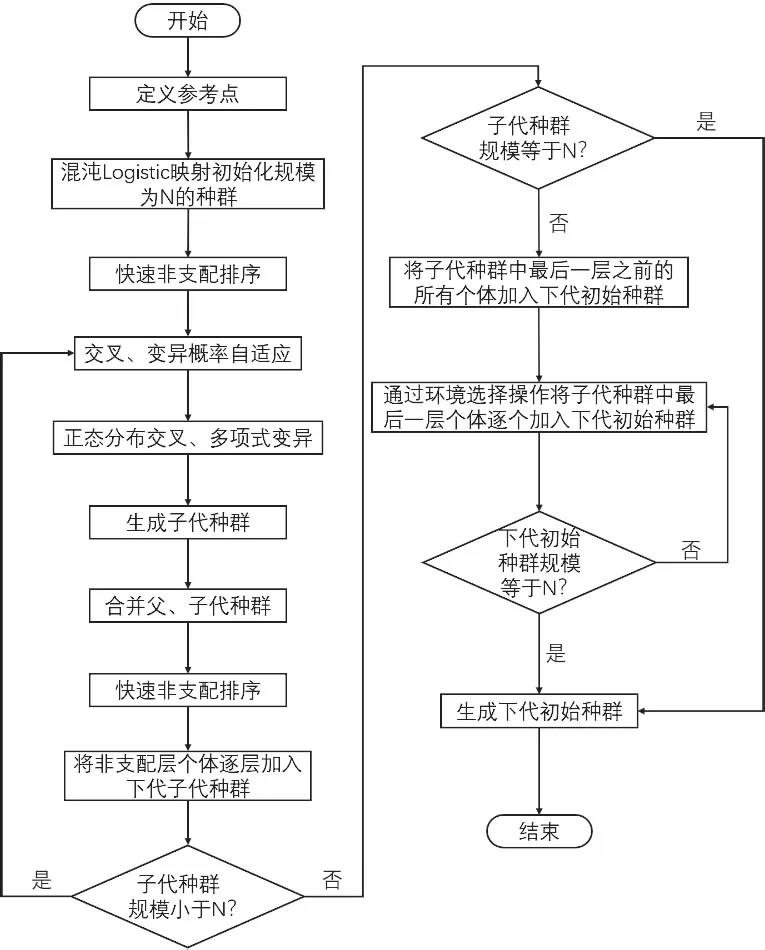
4 案例分析

4.1 案例描述
4.2 周期驱动
4.3 显性扰动驱动

5 结论
