基于多层感知机的绵羊限性性状基因组选择模拟研究

2023-07-31王万年陈思佳郜金荣温中豪袁梦娇张洪志庞志旭乔利英刘文忠

畜牧兽医学报 2023年7期

王万年,陈思佳,郜金荣,温中豪,袁梦娇,张洪志,庞志旭,乔利英,刘文忠

(山西农业大学动物科学学院,太谷 030801)

基因组选择(genomic selection, GS)是利用覆盖于全基因组范围内的遗传标记,结合表型信息对个体育种值进行预测的方法[1]。随着近年来基因分型成本的降低,基因组选择在畜禽育种中得到了广泛应用[2-3]。相对于最佳线性无偏预测(best linear unbiased prediction, BLUP)[4],基因组最佳线性无偏预测(genomic BLUP, GBLUP)模型[5]和一步法基因组最佳线性无偏预测(single-step GBLUP, SSGBLUP)[6]利用了基因型信息,提高了基因组估计育种值的准确性。除BLUP系列方法之外,由于深度学习(deep learning, DL)在许多其他科学领域的应用力量,人工神经网络(artificial neural network, ANN)模型也开始用于GS[7],多层感知机(multilayer perceptron, MLP)是一种前馈神经网络模型,利用了多层神经网络拟合基因组信息和表型信息间的关系计算GEBV。在前人研究中[8],MLP在奶牛生长性状中有更小的基因组预测误差和更高的表型值预测精度[8]。

与生长性状不同,限性性状指在一个物种的一种性别中表达的性状。这些性状由性染色体或仅在一种性别中表达的常染色体基因控制,如单睾、产仔数、产蛋量等。相对于非限性性状,限性性状目前只能在单性别中测定表型,在育种中缺少一个性别的选种,选择效率不高,利用基因组选择可以实现双性别都参与选种。GBLUP、SSGBLUP、MLP在非限性性状基因组选择中,由于可以使用全部的表型数据和与之对应的基因组数据,GS准确性可以达到较高水准,并且SSGBLUP和MLP优于GBLUP;而在限性性状中,表型数据只来自于单性别,GBLUP通过伪表型,SSGBLUP结合了系谱信息,MLP通过神经元学习基因组和表型关系均同时使用了来自公畜和母畜基因组数据,这些不同导致估计方法的GEBV准确性可能会存在差异。许多研究表明,对于易于测量性状和中高遗传力性状,BLUP取得了较好的应用效果[9-10],对于限性性状,BLUP方法应用效果较差[11]。相比于传统BLUP和GBLUP,使用SSGBLUP可以有效提高GS的准确性[12-14],而MLP法在限性性状中的GS效果仍需进一步评估。由于在方法原理和使用条件中差异的存在,检验MLP在限性性状中GS的效果是否优秀,对促进限性性状的选择具有重要意义。

为了估计育种值,需要对遗传参数进行估计,3大遗传参数指遗传力(heritability,h2)、重复力和遗传相关,通常使用估计遗传力(遗传参数)与当代群体真实遗传力(遗传参数)的接近程度衡量遗传评估效果。近年来,遗传参数估计的方法被不断改进,从传统的方差分析法[15]到适用于混合模型的Henderson方法[16]、最大似然法[17]和约束最大似然法(restricted maximum likelihood, REML)[18]。REML法避免了最大似然估计造成的偏低估计,是使用线性混合模型进行遗传参数估计的常用方法。相对于REML法,ANN是非线性模型,没有对SNP标记和表型之间的关系做出先验假设,而是通过神经元的连接分析两者之间的潜在关系,为适应输入和输出之间的复杂关联提供了灵活性[19]。前人研究报道中[14],在计算得出EBV/GEBV后,必须还要对其准确性进行评估,通过EBV/GEBV准确性的高低评判各模型的选择效果。

为了研究MLP在限性性状GS中的有效性,检验MLP在限性性状GS中的应用效果是否优秀,本研究基于多个绵羊模拟群体进行以下研究:1)比较不同情况下MLP与BLUP、GBLUP、SSGBLUP遗传参数估计结果;2)预测不同情况下MLP的GEBV准确性,并对MLP在GS中的使用效果进行评估。

1 材料与方法

1.1 数据模拟

使用QMsim软件[20]模拟3个水平(50、100、500)数量性状基因座(quantitative trait loci, QTL)数目及3个水平(0.05、0.2、0.5)h2的限性性状,性状表型方差标准化为1,对整个模拟过程重复10次,以减少抽样误差。由于模拟群体经过几代之后,当代群体h2与设置值有出入,所以需要计算真实的当代群体h2。为了得到与实际绵羊群体相似的连锁不平衡(linkage disequilibrium, LD)和突变-漂变平衡[21],构建了2 000个世代的绵羊群体,起始规模3 000头,群体规模大小不变,群体构建阶段,公、母数目保持一致,采用随机交配。从构建的群体最后一代随机抽取50头公羊,1 000头母羊作为当代的初始群体,分别构建4个世代的当代群体Pop1和5个世代的当代群体Pop2。模拟中,公、母羊淘汰率均为20%,公、母羊增长率均为40%。公、母羊随机交配,每头母畜后裔数为1,公母后裔各半。选择估计育种值高的个体留种,并按年龄进行淘汰。

本试验模拟绵羊的基因组信息,设置26对常染色体,总长2 584 cM。为了模拟接近真实情况的LD,依据真实染色体长度及数目模拟基因组信息。分别模拟10 000(10K)和50 000(50K)个SNPs标记,假定SNP标记均匀分布在全基因组范围内,且标记无效应。分别设置QTL数目为50、100和500个,QTL的最小等位基因频率(minor allele frequency, MAF)为0.1。假定QTL在全基因组范围内随机分布,QTL效应值服从伽马分布(形状参数为0.4)。为了创建突变-漂变平衡,设置构建群体中QTL和SNP标记的回复突变率为10-5。

在Pop1中选择第2～3世代作为参考群,第4世代作为候选群;在Pop2中选择1～4世代作为参考群,第5世代作为候选群。保留Pop1和Pop2的完整系谱,和参考群中所有母畜的表型信息。选取参考群有后裔的公畜和所有母畜进行基因分型,随机选取候选群的100个个体进行基因分型。本研究只对部分候选群体进行基因分型,更有实践意义。

1.2 基因组预测模型

(1)

其中,

MME的求解通过DMU[22]软件完成。

1.2.2 MLP MLP由输入层(input layer, IL)、隐藏层(hidden layer, HL)和输出层(output layer, OL)组成。IL接收标记信息,HL分别由n1, n2, …, nj神经元组成,OL由代表神经网络输出值的nol神经元组成,输入经过IL被传递给HL1的神经元,然后每个隐藏的神经元产生一个输出,用作HL2的每个神经元的输入,以此类推最终得到输出值yi。在这种结构中,每一层均产生权重w[i]矩阵,其中输出由最后一个HL的线性组合产生。最终得到的预测值为:

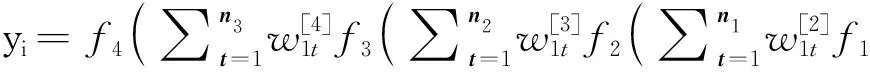
(2)

其中,bi代表第i层的偏置,初始偏置设置为1,w[i]代表第i层权重,fi为激活函数,p代表IL神经元个数,t表示第t个神经元。在本试验中,采用含3个HL的MLP架构,IL、HL1、HL2、HL3、OL神经元个数依次为64、32、32、16、1。为了防止模型过拟合,在第一隐藏层到第二隐藏层间增加了随机失活层,训练时设置为0.2,即保留80%的节点,其余的20%置为0。

本研究中使用修正线性单元(rectifier linear unit, ReLU)激活函数[23],增加了神经网络各层之间的非线性关系。

(3)

采用均方误差(mean square error, MSE)作为损失函数,平均绝对误差(mean absolute error, MAE)作为评估函数,在反向传播过程中,损失函数En对输出层输出yi的求偏导,得到输出yi与真实值yt的差值δi=yi-yt,若设定zi=ReLU(x),则损失函数对隐藏层输出ai的偏导为:

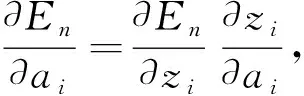
(4)

损失函数对网络权重w[i]的梯度为:

(5)

为了使模型输出逼近最优值,采用了均方根传递(root mean square prop, RMSProp)算法[24]来更新模型的网络参数。RMSProp除了自适应调节学习率之外,对权重w和偏置b的梯度计算了微分平方加权平均数,用以修正摆动幅度,加快函数的收敛。

E[g2]t=αE[g2]t-1+(1-α)g2

(6)

(7)

(8)

1.3 遗传参数估计方法

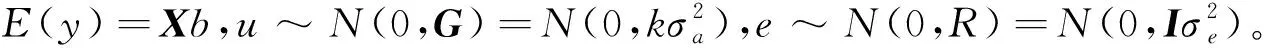
(9)

其中,

P=V-1-V-1X(X-1V-1X)-1XTV-1

(10)

(11)

IAE=λIEM+(1-λ)IAI

(12)

其中,IEM是EM算法的期望最大阵,IAI是AI算法的平均信息阵。λ∈[0,1],设置λ以一定步长增长。直到迭代后的方差组分估计值在参数空间内。

1.3.2 ANN 在ANN中,估计h2和SNP效应,需要获得标记的相对重要性(relative importance, RI)。Olden等[29]提出了一种方法,即使神经网络有多个HL,可以使用所有的连接权重来获得RI。连接权值矩阵的优劣决定了SNP效应估计的准确性,为了计算所有标记的RI向量,将连接权重矩阵相乘。即

RI=w[1]*w[2]*…*w[j-1]

(13)

其中,将w[i=1]作为连接第j-1层到第j层的的估计权值矩阵,j是人工神经网络的层数。使用如下线性近似[29],通过RI值估计加性SNP效应向量βα,即:

(14)

(15)

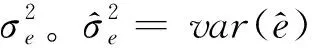
1.4 模型评价

1.4.1h2比较 10次重复下,各方法计算当代群体估计h2的均值和标准误在相同条件下与真实h2进行比较并做显著性检验,h2估值越接近真实h2越准确,h2估值越准确说明遗传评估效果越好。各方法估计h2与真实h2差异越显著,说明遗传评估效果越差。

1.4.2 候选群体EBV/GEBV准确性比较用EBV/GEBV准确性来比较不同模型的性能。准确性通过EBV/GEBV与QMsim软件中模拟的TBV之间的相关系数衡量。即

从不同QTL数目、不同标记数与不同遗传力3个角度,对Pop1和Pop2进行育种值估计,计算其候选群EBV/GEBV准确性。相同条件下,准确性越高说明模型性能越好。

2 结果

2.1 参考群体和候选群体

2个独立的当代群体Pop1和Pop2群体结构模拟结果见表1。其中Pop1的参考群个体为3 360个,基因分型个体为1 866个,候选群个体为2 744个,基因分型个体为100个;Pop2的参考群个体为7 154个,基因分型个体为3 351个,候选群个体为3 842,基因分型个体为100个。

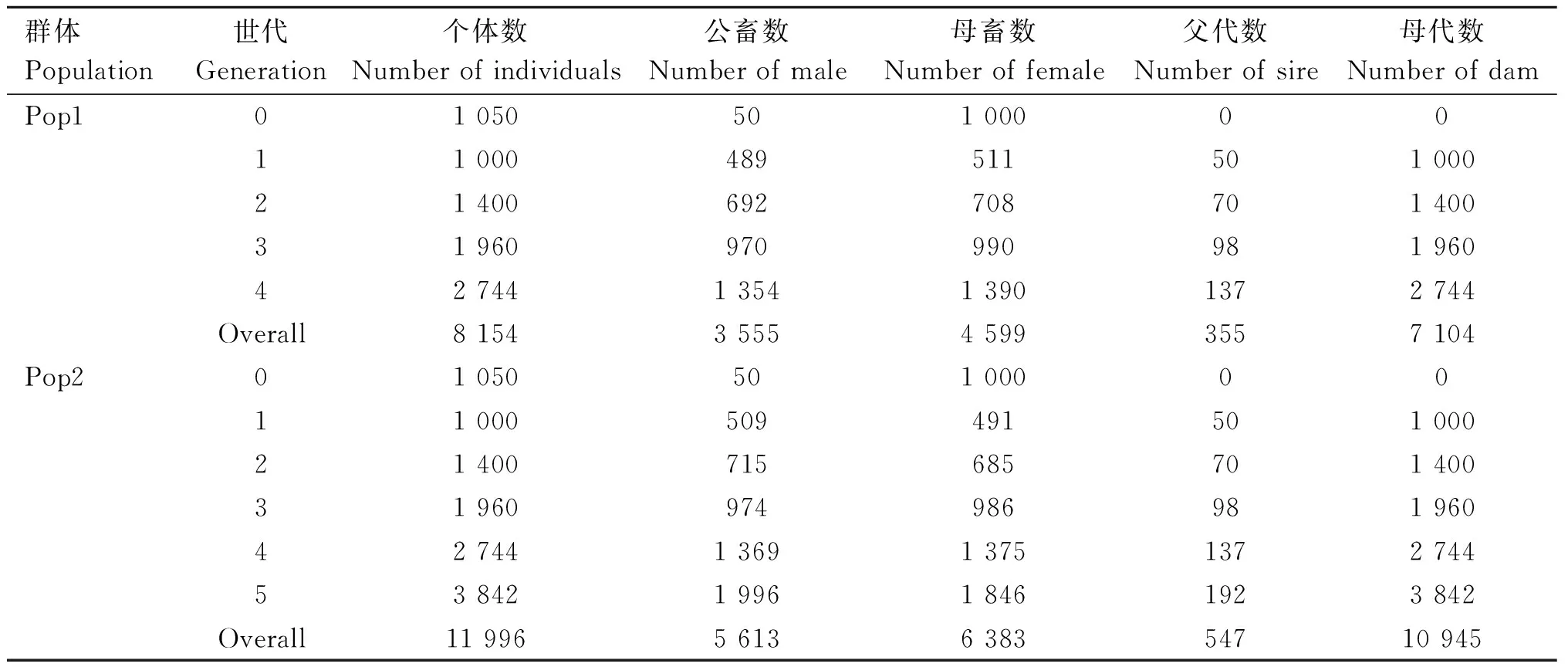
表1 模拟数据的当代群体结构Table 1 Structure of recent population obtained from QMsim

2.2 MLP模型评估

如图1所示,MSE最终达到了0.002 7,MAE最终达到了0.037 2,损失函数和评估函数在训练600次之后基本均趋于平缓,模型拟合效果良好。

图1 MLP模型损失函数与评估函数结果Fig.1 MLP model loss function and evaluation function results

2.3 不同情况下各模型的h2估计结果

设定初始群体特定限性性状h2为0.05时,MLP、SSGBLUP、GBLUP和传统BLUP的h2估计结果见表2。4种方法的估计值介于0.028～0.075,与当代群体遗传力0.047～0.051相符。MLP的估计值介于0.044～0.057,相比SSGBLUP介于0.041～0.068范围更小。在QTL数目和标记数相同的情况下,Pop1(Pop2)中当代群体遗传力为0.049～0.051(0.047～0.050),与MLP的h2估值0.044～0.057(0.046～0.055)差异不显著。在Pop2群体中标记数为10K且QTL数为100时,SSGBLUP与MLP差异不显著,但两种方法均显著(P<0.05)优于GBLUP和BLUP;除此之外,MLP的h2估计结果均显著(P<0.05)优于SSGBLUP、GBLUP和BLUP。

表2 设定初始群体特定限性性状h2为0.05时各模型h2估计结果Table 2 Estimation results of h2 of each model when the prior population-specific limit trait h2 is set to 0.05

设定初始群体特定限性性状h2为0.2时,各方法h2估计结果与当代群体h2的对比见表3。在QTL数和参考群大小相同的情况下,SSGBLUP和GBLUP法遗传力估计结果在不同标记数下差别较大,MLP差别较小。在Pop1群体中标记数为10K且QTL数为50时,MLP的h2估值与当代群体h2差异显著(P<0.05);除此之外,在QTL数目和标记数相同的情况下,Pop1(Pop2)中当代群体遗传力为0.196～0.207(0.194～0.207),与MLP的h2估值0.196～0.216(0.185～0.203)差异不显著。在Pop1中QTL数为500的两个标记数下和Pop2中QTL数为10且标记数为50K两种情况下,MLP的h2估值与SSGBLUP差异不显著,但两种方法均显著(P<0.05)优于GBLUP和BLUP;除此之外,MLP的h2估计结果均显著(P<0.05)优于SSGBLUP、GBLUP和BLUP。

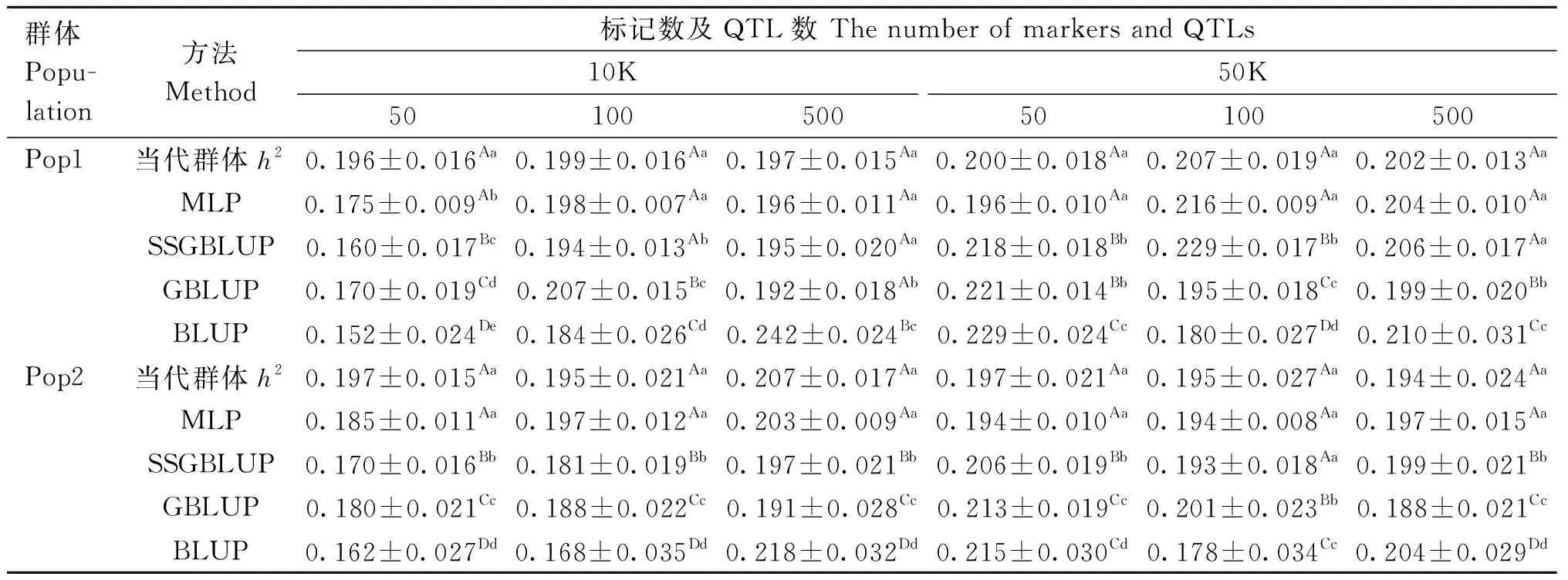
表3 设定初始群体特定限性性状h2为0.2时各模型h2估计结果Table 3 Estimation results of h2 of each model when the prior population-specific limit trait h2 is set to 0.2

设定初始群体特定限性性状h2为0.5时,各方法h2估计结果见表4。在QTL数及标记数相同的情况下,4种方法在Pop2群体中的遗传参数估计结果较Pop1更接近于真值。QTL数为100,Pop1中标记数10K下和Pop2中标记数50K下,MLP的h2估值与SSGBLUP差异不显著,但两种方法均显著(P<0.05)优于GBLUP和BLUP。除此情况之外,MLP的h2估计结果均显著(P<0.05)优于SSGBLUP、GBLUP和BLUP。

2.4 不同模型预测效果

表5为不同h2初值时,各方法的预测准确性范围。在QTL数目和标记数相同的情况下,h2初值为0.05时,MLP的GEBV准确性较SSGBLUP和GBLUP明显提高;h2初值为0.2时,MLP的GEBV预测准确性较SSGBLUP有略微提高,较GBLUP有明显提高;h2初值为0.5时,MLP的GEBV准确性较SSGBLUP没有明显提高,较GBLUP和BLUP优势明显。

表5 不同h2初值时各方法预测准确性范围Table 5 When different prior h2 values, the prediction accuracy range of each method

图2为不同情况下MLP、SSGBLUP、GBLUP的GEBV准确性及BLUP的EBV准确性,在h2、QTL数和标记数相同的情况下,Pop1和Pop2群体中,MLP的预测准确性均为最高,BLUP均为最低;Pop2群体中各方法的预测准确性较Pop1群体均有提升。在QTL数、标记数和群体相同的情况下,随着h2降低,MLP较GBLUP和SSGBLUP的GEBV准确性差值变大,优势逐渐增加。在h2、QTL数和群体相同的情况下,MLP、SSGBLUP及GBLUP模型在标记数为50K时的准确性较标记数为10K时有提高。其中,在QTL数目相同及h2初值为0.05时,Pop1(Pop2)群体中MLP在标记数为10K时预测准确性介于0.269～0.278(0.287～0.300)略高于SSGBLUP在标记数为50K的预测准确性0.224～0.241(0.262～0.279)。在h2、标记数和群体相同的情况下,预测准确性随QTL数改变并没有明显变化。

3 讨论

在绵羊育种中,限性性状是影响经济效益的重要性状,这种复杂性状的遗传增益可以有效的提高绵羊的生产效率[30]。除产奶量外,乳房构型、产羔困难和乳腺炎等限性性状对生产成本和动物福利影响同样很大,也需要在育种目标中加以考虑[31]。在绵羊中实施基因组选择最严峻的挑战是品种问题,许多品种个体数少,导致参考群小,连锁不平衡低,有时甚至缺乏表型记录[32]。用MLP进行GS[8]已有报道,但是在绵羊限性性状中还未应用,所以本研究在不同h2、QTL数目、标记数的两个群体(Pop1和Pop2)中对MLP模型进行了全面的测试。研究发现,在QTL数、标记数和群体相同的情况下,在3个h2水平下,MLP较GBLUP和SSGBLUP优势更大;随着h2降低,MLP较GBLUP和SSGBLUP的优势逐渐增加,表明DL方法的实施为改善绵羊限性性状的遗传增益提供了巨大潜力。

遗传参数估计是家畜育种中的重要组成部分,群体遗传参数估值的优劣对正确评定种畜育种值和育种规划有非常重要的作用。MLP是通过神经元权值矩阵计算SNP效应向量从而进行遗传参数估计;而REML法是对线性模型求解约束似然函数,通过迭代的方式求解其极值点计算方差组分。本研究中,4种方法在Pop2群体中的遗传参数估计结果较Pop1更接近于真值,表明在估计遗传参数时MLP与SSGBLUP、GBLUP和BLUP同样受参考群体大小的影响,参考群体越大,遗传参数估计结果与当代群体遗传参数的差值越小[33]。除个别情况之外,MLP的遗传力估计结果与其他3种方法差异显著,且在相同h2、QTL和标记数下,对于Pop1和Pop2两个群体MLP的遗传参数估值与群体遗传参数的差值较SSGBLUP、GBLUP和BLUP均更小,表明MLP在遗传参数估计上优于其他3种方法,这可能是因为多层人工神经网络采用非先验假设很好的解释了非加性效应,弥补了线性模型的局限性[34]。Gholizadeh等[35]在奶牛中应用神经网络,得到了准确的产奶量遗传力估计结果。Coelho de Sousa等[36]在咖啡中应用MLP进行遗传力估计,得到的结果优于GBLUP,这是因为标记物之间的相互作用隐含在神经元多次加权的输出中。

Pérez-Rodríguez 等[37]通过小麦数据集对神经网络和几种线性模型进行了评估,发现在植物中非线性神经网络比线性模型有更好的预测精度。McDowell[38]使用拟南芥、玉米和小麦数据对常规基因组预测模型与MLP进行了比较,在3个性状中,MLP的预测准确性均高于传统的基因组预测模型。预测准确性结果显示,相同h2、QTL和标记数下,相比于Pop1群体,具有更大参考群规模的Pop2群体中4种方法的GEBV准确性均有提高,由此推测低遗传力性状需要更多的表型数据来提高准确性。Luan等[39]使用挪威红牛数据应用GBLUP及Bayes模型时也显示出与本研究相似的结果,对于h2更高的性状和更大参考群体,育种值估计更准确。本研究在不同QTL数下各模型获得的准确性无明显变化,可能是因为试验中假设所有标记解释相同的效应方差且无主效基因。在Daetwyler等[40]的模拟研究中,GBLUP在不同QTL数目时,准确性基本无变化,与本研究结果相符。随着标记数从10K增加至50K,4种方法整体上基因组估计育种值准确性均呈上升趋势,在张猛[41]的研究中也得到了相同的结论。在h2为0.05时,MLP在标记数为10K时的准确性略高于其他方法在50K时的准确性,这可能是由于标记数过少造成SSGBLUP法性能的下降。

相对于非限性性状,在限性性状中想要使遗传评估和育种值估计结果达到更高水平难度更大,虽然使用GS利用双性别的基因型数据弥补了一部分表型缺失的劣势,但是育种值准确性的提高仍然有限[13]。在方法上,各模型对非限性性状进行正常流程的遗传评估和基因组选择,而对于限性性状,GBLUP必须使用EBV[42]或逆回归育种值[43-44]作为伪表型值,通过伪表型值和基因组信息得到基因组估计育种值。SSGBLUP将系谱信息与基因组信息整合到模型[6]中,构建基因组关系矩阵(H阵),结合表型信息预测未进行基因分型个体的EBV及基因分型个体的GEBV。MLP是使用输入数据为该网络寻找最佳权重,它将输入的多个数据集映射到单一的输出数据集上,每个神经元的输出表示为神经元全部输入的加权和,通过线性和非线性激活函数[45-46]调节预测变量的特定权值从而学习基因型和表型之间的关系。在结果上,结合前人研究[47],非限性性状的GEBV准确性较限性性状更高,这是由于使用伪表型值或非线性学习模式均不能完全弥补表型的缺失。

在模拟研究中,非线性模型优于线性模型[48],而在真实数据中,非线性模型较线性模型只有轻微优势或没有优势[49]。无论哪种模型都是简化模型,与真实模型会有较大差异,可能更接近复杂生物现象的其他模型尚未找到,还需要继续大量研究。本研究中MLP法的优势和有效性仍然需要在真实绵羊群体中进行验证。