基于有限差分法的填土边坡复合结构受力特征分析

李漪,柴平稳,李珂,贺修安,王红伟

(1.湖北省电力勘测设计院有限公司,武汉 430040;2.国网经济技术研究院有限公司,北京 102209;3.中国地质大学(武汉)工程学院,武汉 430074)

边坡在天然情况下总是处在一定的应力平衡状态,这种初始的应力状态是由岩土体自重应力场与构造应力在长期的相互作用中形成的,但在外界诱发因素作用下,会打破边坡原始应力状态,导致边坡失稳,最后演变成地质灾害,影响人类正常的生产生活。

边坡稳定性问题一直是学者们研究的重点[1-6],挡土墙是一种稳定边坡的支档结构,在地质灾害治理中扮演着重要角色,在对挡土墙结构设计时需要考虑实际工程地质条件的影响,一般而言,在治理地基承载力较高的失稳边坡时,单一的挡土墙结构可以满足安全需求,但是工程实践中常常会遇到地基软弱层,若挡土墙修建在这种地基上,难以保证边坡及整个支档结构的长期稳定性,而抗滑桩可以穿过软弱层并深入基岩,可以有效稳定边坡[7-11]。有设计者提出了桩基托梁挡土墙结构,即当需要修建挡土墙所在场地的地基承载力不足时,在挡土墙下设置桩基础,此时桩基础可以有效提高挡土墙整体稳定边坡的能力。对于此类结构,中外学者给予了高度关注。梁永辉[12]根据上海实际工程中的高填方边坡可能的失稳破坏特征,提出了桩承式挡土墙支档结构治理边坡的设计方案,并对边坡与防护措施相互作用关键问题进行总结。刘国楠等[13-14]为研究衡重式桩板挡墙受力特征,进行了与原型呈一定比例的室内模型试验,研究了该支档结构土压力分布模式,并更细节的探讨不同桩板尺寸、位置以及不同外荷载工况下对墙后土压力的影响。董捷等[15]在对桩板墙加固填方边坡中的土压力问题进行试验研究,得出当桩间采用柔性挡土板时能够提高整体加固结构的稳定性,研究中还对施工期间桩前桩后土压力特征进行探讨,进一步明确了土压力随深度的变化特征。罗强等[16]研究了平动位移下衡重式挡墙背土体破裂面特征及土压力的分布。

有关挡土墙受荷的研究多是基于试验或者力学平衡原理求解挡土墙土压力的大小,这是研究这种新型支档结构的基础,在研究托梁和桩基时,理论上将二者视为结构单元,在计算其受力特征时常常将两者简化为梁模型,不同的是,托梁常被视为水平地基上的横梁,桩基被视为纵梁[17-18],理论计算中均是基于Winkler理论进行计算。余文杰[19]将托梁和桩基视为Winkler弹性地基上的梁模型,并采用初参数解法,给出了桩基托梁和桩基不同截面处挠度、转角、剪力和弯矩的解析解,并用ABAQUS有限元软件开展了桩基托梁挡土墙的数值研究;吴云峰[20]以某变电站高填土边坡桩基托梁挡土墙为研究对象,将托梁简化为连续梁和Winkler弹性地基梁,并将两种梁模型进行理论对比计算。胡雪[21]也将桩基视为梁模型,采用理论与数值计算相结合研究桩基受力特征。

鉴于以上情况,首先阐述挡土墙所受土压力基本计算方法,将土压力水平和竖直荷载分别视为托梁和桩基的输入荷载,简化托梁和桩基为梁模型,基于有限差分法分别对托梁和桩基内力进行求解,最后将本文理论应用于实际工程案例研究。研究成果丰富了桩基托梁挡土墙设计理论,可为实际工程边坡防护提供指导。

1 桩基托梁挡土墙结构

1.1 桩基托梁挡土墙特征

桩基托梁挡土墙是一种由桩基、托梁及挡土墙组成的新支档结构,其综合了挡土墙与桩基托梁结构的技术特点,不稳定土体荷载先由挡土墙承担,随后由挡土墙传递到托梁,再传递到桩基上,桩底嵌入稳定岩层内,岩层反力使得桩基托梁挡土墙整体结构稳定,可有效加固边坡,是一种较优的支档结构,常用于填土边坡较高且下方地基承载力较小的情况,其常见的支护形式如图1所示。

图1 桩基托梁挡土墙结构图Fig.1 Structure drawing of pile joist retaining wall

1.2 挡土墙土压力计算理论

作用在挡土墙上的荷载主要为土压力,如何计算土压力对挡土墙的尺寸设计具有重要的指导意义。目前,关于挡土墙土压力的计算模式较为系统和成熟,一般采用库伦土压力理论和朗肯土压力理论进行计算,土压力大小与挡土墙类型、场地地形以及土体性质等有关。对于扶壁式挡土墙而言,其三维结构如图2所示。

图2 扶壁式挡土墙结构示意图Fig.2 Structural schematic diagram of buttress retaining wall

有关扶壁式挡土墙的土压力计算问题,较为认可的计算方法是参照《建筑边坡工程技术规范》(GB 50330—2013),如图3所示,挡土墙向后延伸较长,形成L形挡土墙,并假定AB为墙背,且发生第二破裂面,此时墙背摩擦角与土体内摩擦角相等[19]。

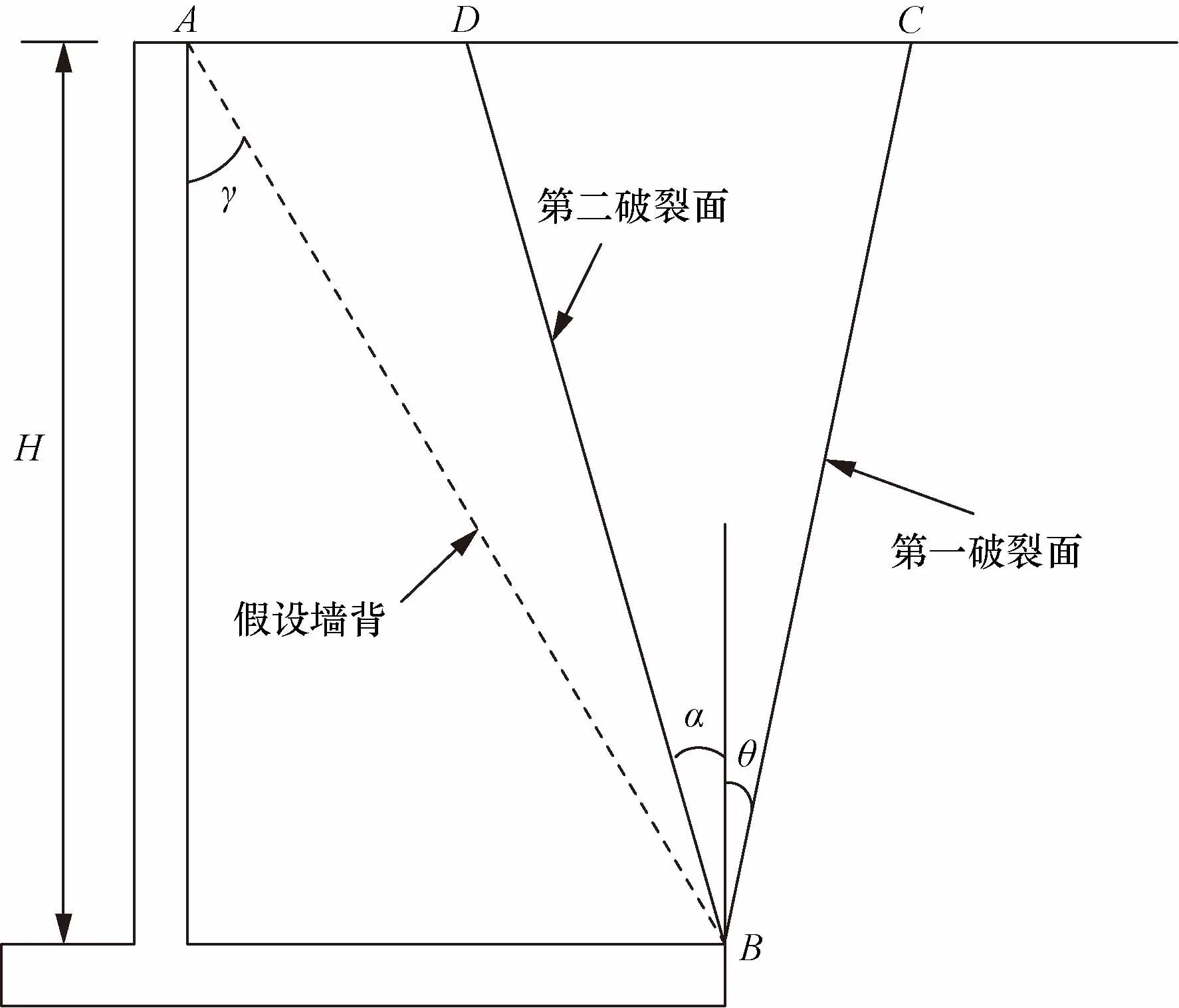
α为第二破裂面与竖直线的夹角;H为墙身高度;θ为第一破裂面与竖直线的夹角;γ为墙背与竖直线的夹角;H为挡土墙高度图3 扶壁式挡土墙土压力计算简图Fig.3 Calculation diagram of earth pressure on buttress retaining wall

根据图3可以确定墙后土体可能的第一破裂角及第二破裂角,其表达式分别为

(1)

式(1)中:φ为土体内摩擦角;β为墙后填土表面与水平线的夹角;ε为破裂面夹角,其表达式为

(2)

当γ>α,表示第二破裂面与填土夹角位于AC之间,此时破裂面自由出现;当γ≤α时,此时可假定墙背作为第二破裂面,则土压力计算表达式为

(3)

式(3)中:Ex为墙后水平主动土压力;Ey为墙后竖向主动土压力;δ为墙后土体容重;Ea为作用于破裂面上的土压力,可表示为

(4)

式(4)中:W为破裂土体自重。

2 基于有限差分法的理论计算

2.1 基于有限差分法的托梁内力计算理论

托梁处于挡土墙和下方基桩的中间,主要起连接作用,可将作用于挡土墙的荷载传递到桩体上,在分析托梁受力特征时,分为连续梁和弹性地基梁两种计算方法对托梁内力进行计算,托梁及桩基三维示意图及二维平面图如图4和图5所示[19]。

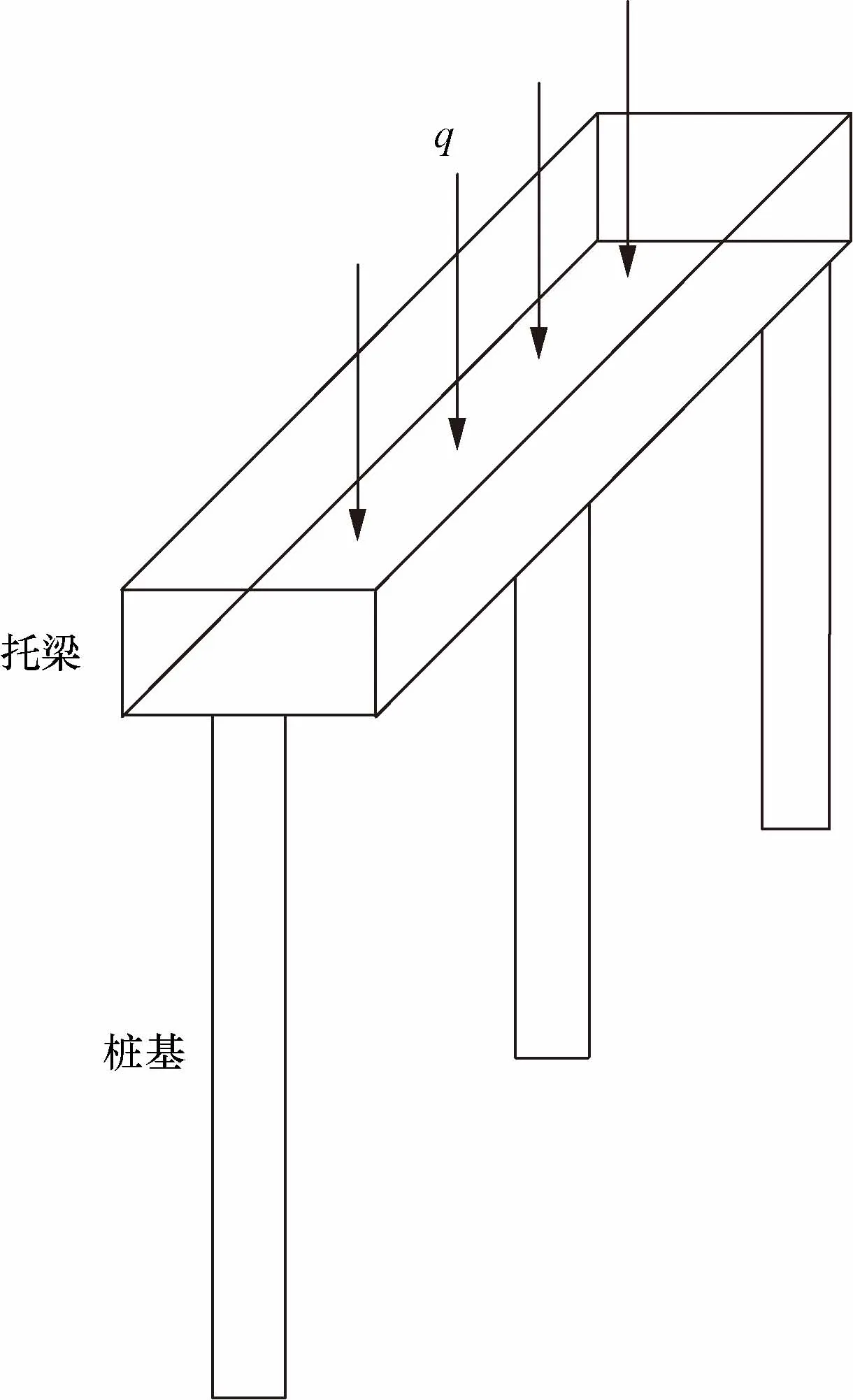
q为托架上覆匀部荷载图4 桩基托梁结构图Fig.4 Structure diagram of pile foundation joist

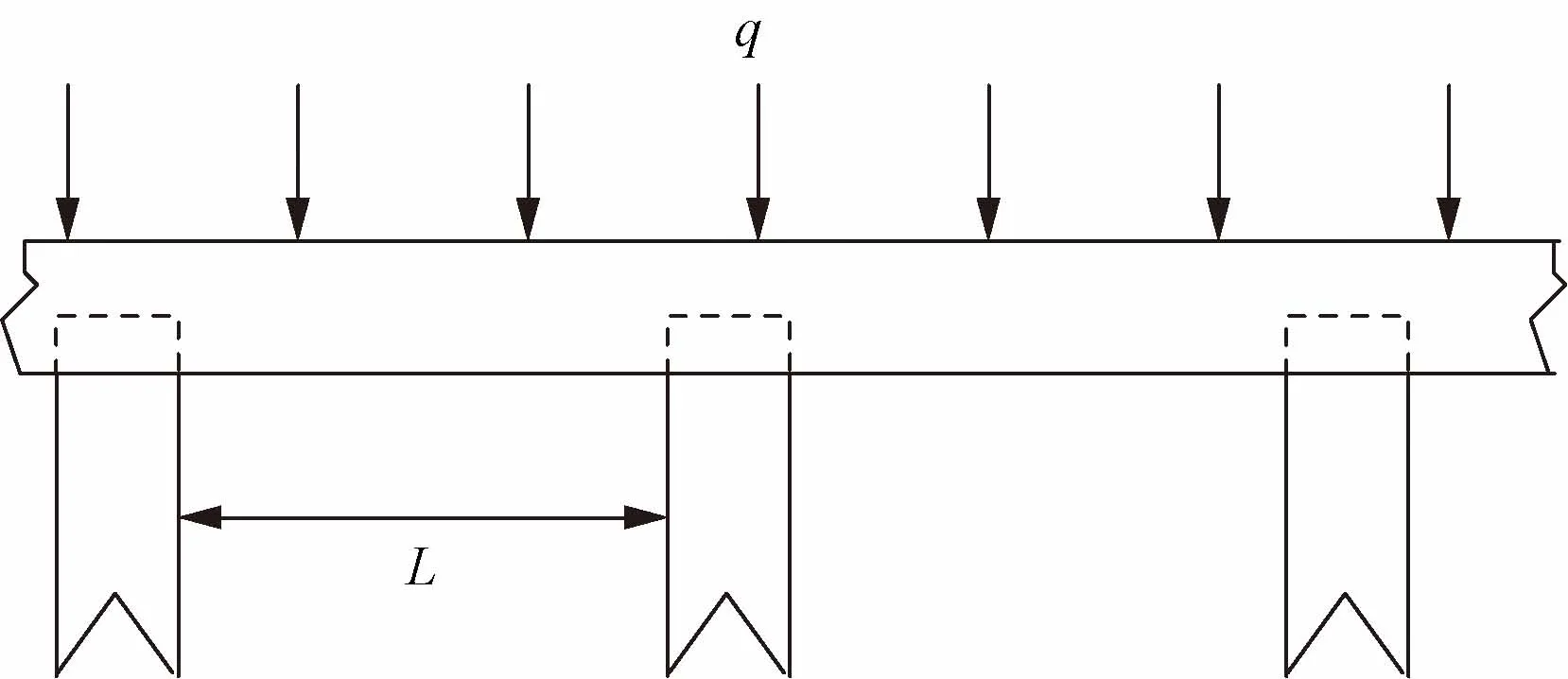
L为计算跨度图5 托梁桩基简化受力简化图Fig.5 Simplified load diagram of joist pile foundation

2.1.1 托梁连续梁理论

连续梁理论忽略地基土的支撑作用,将桩基支撑作用视为主要的支撑荷载,这种计算方法简化了地基对托梁的作用效果,根据连续梁内力计算假定,可以得到梁内力的计算公式,如式(5)～式(7)所示。

支座弯矩的计算公式为

(5)

跨中弯矩的计算公式为

(6)

支座剪力的计算公式为

(7)

2.1.2 托梁弹性地基梁理论

弹性地基梁理论考虑地基对托梁的支撑作用,则桩基对托梁的作用可看作是边界条件,任意两桩基之间的托梁可用弹性地基梁理论进行计算,则土体对托梁作用可视为具有一定刚度的弹簧,计算力学模型如图6所示。

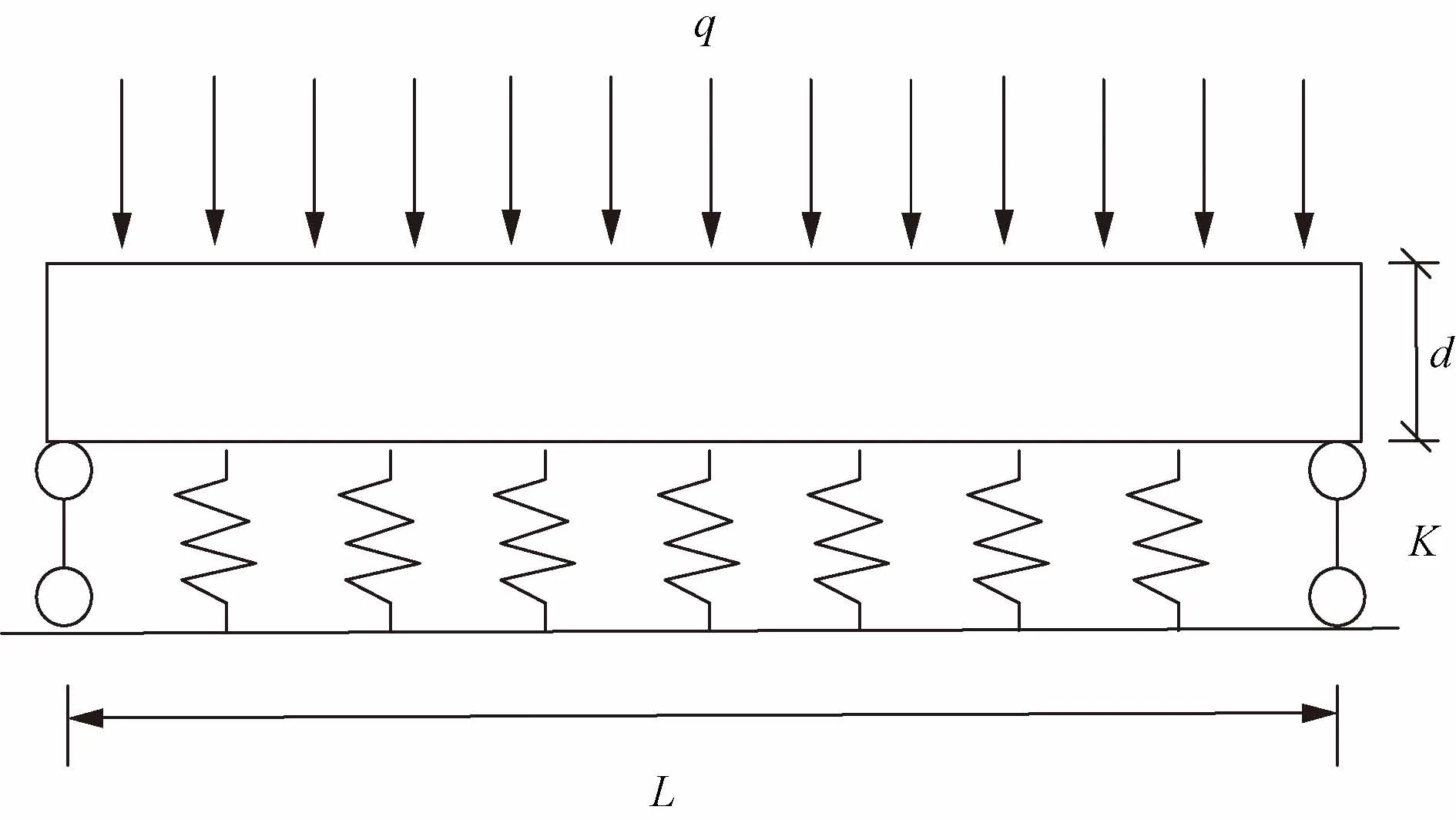
d为托梁宽度图6 托梁计算模型Fig.6 Calculation model of joist

根据Winkler弹性地基梁理论,梁的变形和地基的变形同等变化,地基变形只与该点受力相关,则地基对托梁的反力可表示为

P(x)=Ku(x)

(8)

式(8)中:K为地基的基床系数;u为梁截面的变形;x为横坐标;P为地基反力。

根据力学平衡条件,则可以推出均布荷载下Winkler弹性地基梁的扰曲微分方程为

(9)

式(9)中:E为托梁的弹性模量;I为托梁的惯性矩。

根据梁基本变形理论,梁截面的弯矩和剪力与变形量之间的关系为

(10)

式(10)中:M为托梁的弯矩;Q为托梁的剪力。

式(10)为4阶偏微分方程,难以求得函数表达式,为了简化计算,可根据差分原理将微分方程转化为代数方程进行求解,对于4阶差分,需要5个节点参与,可在此虚拟节点对托梁受力特征进行分析,对于长为L的托梁,可离散如图7所示。

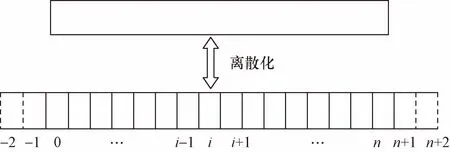
图7 托梁离散示意图Fig.7 Discrete diagram of joist

则式(9)微分方程可表示为

(11)

式(11)中:ui为任意差分节点处的变形;l为差分节点宽度;qi为任意差分节点处的荷载。

剪力和弯矩同样可写为差分形式如式(12)所示。

(12)

托梁是被看作是两端固定支撑的梁模型,其边界条件视为固定端,则两端位移和转角均为0,有如式(13)、式(14)所示的关系成立。

两端位移为0,有

(13)

式(13)中:u0和un分别为差分节点0和n处的变形。

两端转角为0,有

(14)

令式(13)中i=0,再结合式(15)、式(16)可以得到虚拟节点u-1、u-2、un+1和un+2的表达式。

将式(13)写为矩阵的形式有

(Ka+Kb)u=q

(15)

式(15)中:Ka为托梁位移刚度矩阵;u为托梁位移矩阵;q为托梁受荷载矩阵;Kb为托梁抗弯刚度矩阵。

(16)

(17)

q=d[q1,q2,…,qn-1]T

(18)

式(18)中:匀部荷载作用下qn=q。

求解式(15),则可以得到托梁变形结果,再根据式(14)进一步可计算得到托梁的弯矩及剪力。

2.2 基于有限差分法的桩的内力计算理论

在填土边坡工程当中,填土层区域采用挡土墙支护,填土区域下方岩层岩性一般为软弱层,挡土墙修建在该地基上存在地基承载力不足使得挡土墙存在失稳可能,采用桩基托梁挡土墙结构可让挡土墙所受荷载通过托梁及桩基最后传递到下方最稳定基岩层中,若采用单排抗滑桩结构,其支护结构模型可简化为图8。

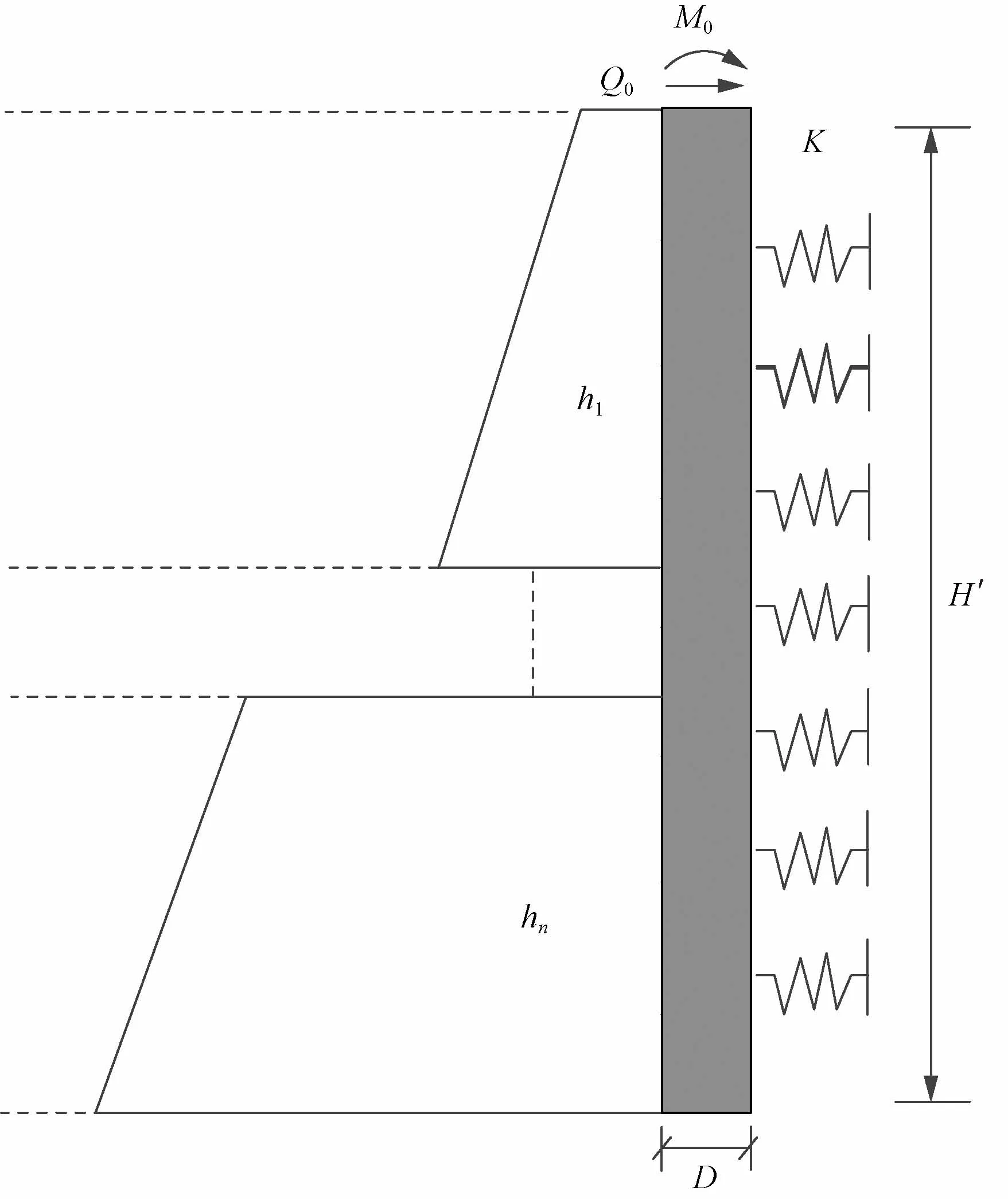
H′为抗滑桩深度;hi为抗滑桩桩后各岩层深度,i=1,2,…,n;D为抗滑桩宽度;K为抗滑桩地基系数图8 桩基计算力学模型Fig.8 Computational mechanical model of pile foundation

假设在桩顶受到挡土墙传递的水平力作用,对于位于土层中桩受到土的抗力作用,其抗力可表示为

P(x,z)=K(z)Dw(x)

(19)

式(19)中:x为水平坐标点;z为深度坐标点;P(x,z)为桩周土的抗力;K(z)为土层地基系数;ω(x)为桩的水平位移;D为桩身宽度。

根据欧拉梁微段平衡方程,可建立在外载作用下桩身变形控制微分方程如式(20)所示。

(20)

式(20)中:G(x)为抗滑桩所受水平荷载。

地基的基床系数K(y)随深度z线性增加,则K(y)=mz,其中m为土层的基床比例系数。

则式(20)可进一步写为

(21)

假设桩基位于均匀埋地岩层中,桩顶和桩底分别满足式(22)所示的边界条件。

桩顶处边界条件为

(22)

桩底视为固定边界,位移和转角均为0,有

(23)

同样基于有限差分原理,将桩基离散为多个差分节点,考虑到一个节点的计算需要多个节点参与,分别在桩顶和桩顶多给出2个节点,桩基离散化及虚拟节点如图9所示。

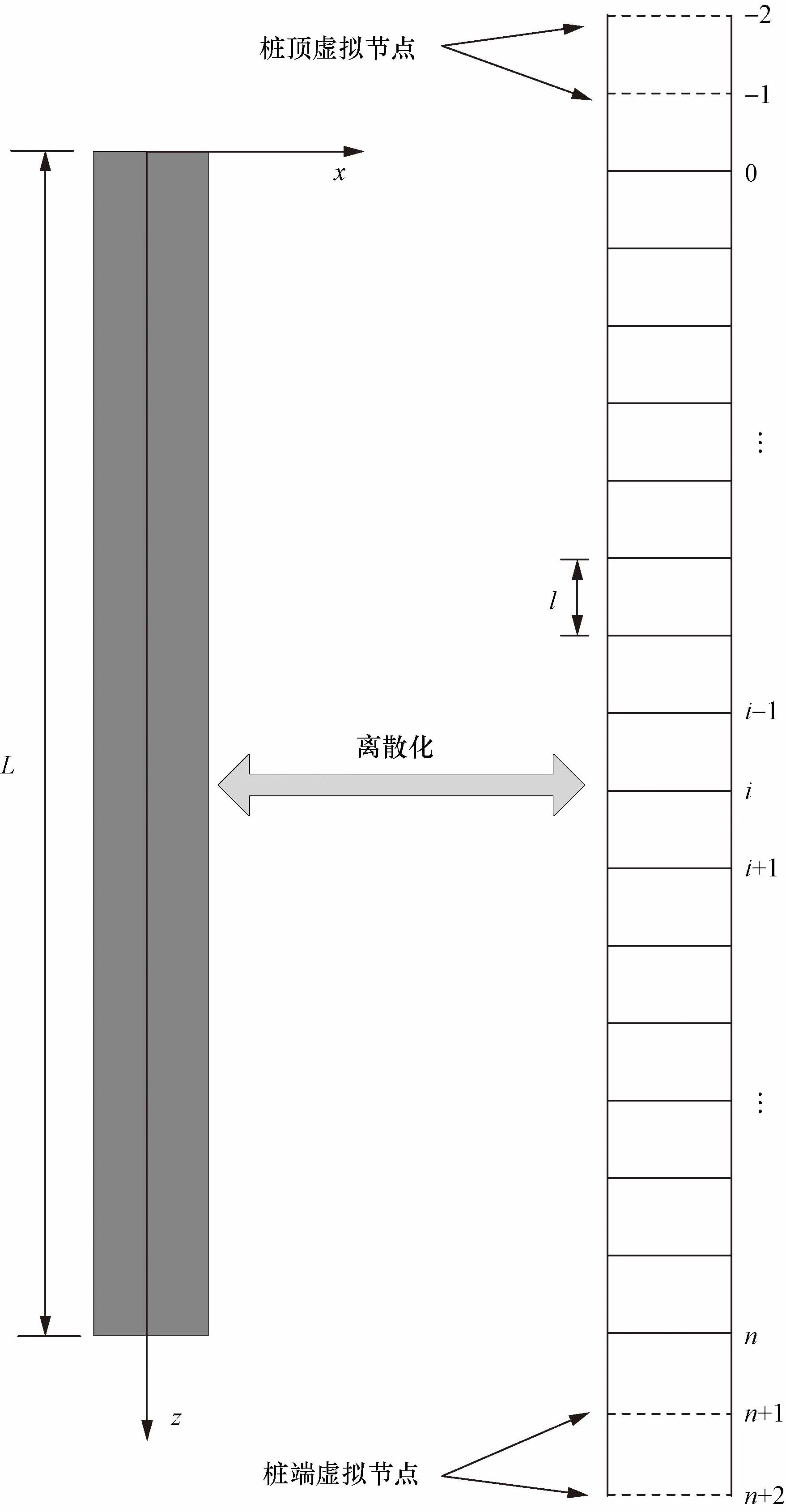
n为差分节点个数图9 抗滑桩离散化Fig.9 Anti-slide pile discretization

用差分格式可表示为

imilDwi=DGi

(24)

式(24)中:ωi为抗滑桩任意差分节点处的变形;mi为抗滑桩差分第i节点处地基系数;Gi为任意差分节点处的水平荷载。

桩顶边界条件用差分格式可写为

(25)

根据式(25)可以得到虚拟节点的表达式为

(26)

根据桩底边界条件,桩底虚拟节点的表达式为

(27)

令式(24)中i=0,再结合式(26)可以得到桩顶和桩底虚拟节点ω-1、ω-2、ωn+1和ωn+2的表达式。

将式(26)写为矩阵的形式有

(Kza+Kzb)w=G

(28)

式(28)中:Kza为桩基位移刚度矩阵;Kzb为桩基抗弯刚度矩阵;w为桩基位移矩阵;G为荷载矩阵。

(29)

(30)

G=D[g0,g1,G2,…,Gn-3,Gn-2,Gn-1]T

(31)

求解式(28)～式(31)所示的矩阵方程,则可以得到抗滑桩变形计算结果,再根据式(12)进一步可计算得到抗滑桩的弯矩及剪力。

3 工程实例

某变电站站址原始地貌属于丘陵地貌,地势起伏较大,站址范围原为水泥有限责任公司场地,现已废弃。现地形为原场地开山堆填而成。整个站址东高西低,呈三级台阶状,第一级台阶坡脚自然标高约374 m,变电站场平标高364.5 m。场平后,变电站南侧将形成最大高度约25 m的填方边坡,该边坡整体表现为东高西低;坡脚高程约364.5 m,后缘高程约395 m,地表坡度从边坡后缘至前缘近似呈两段直线,边坡坡度在20°～45°,边坡后缘为拟修变电站,边坡所在场地如图10所示。

图10 边坡所在场地图Fig.10 Site map of the slope

由于填土堆积时间过短,在其自重和外力作用下,如雨水渗入浸泡,会产生沉降变形及不均匀下沉,导致地坪开裂,使埋置于填土内的基础设施产生破坏或变形。设计采用“扶壁式挡墙+支护桩”进行支护。墙高10 m,墙宽0.8 m,底板高1.2 m,挡墙下接长3 m,高为0.6 m的托梁,托梁下支护桩采用“双排桩”型式,方桩桩径1 m,桩排距3 m,桩长12 m,扶壁式挡墙断面及土层分布如图11所示,计算参数如表1所示。

表1 计算参数Table 1 Calculation parameters

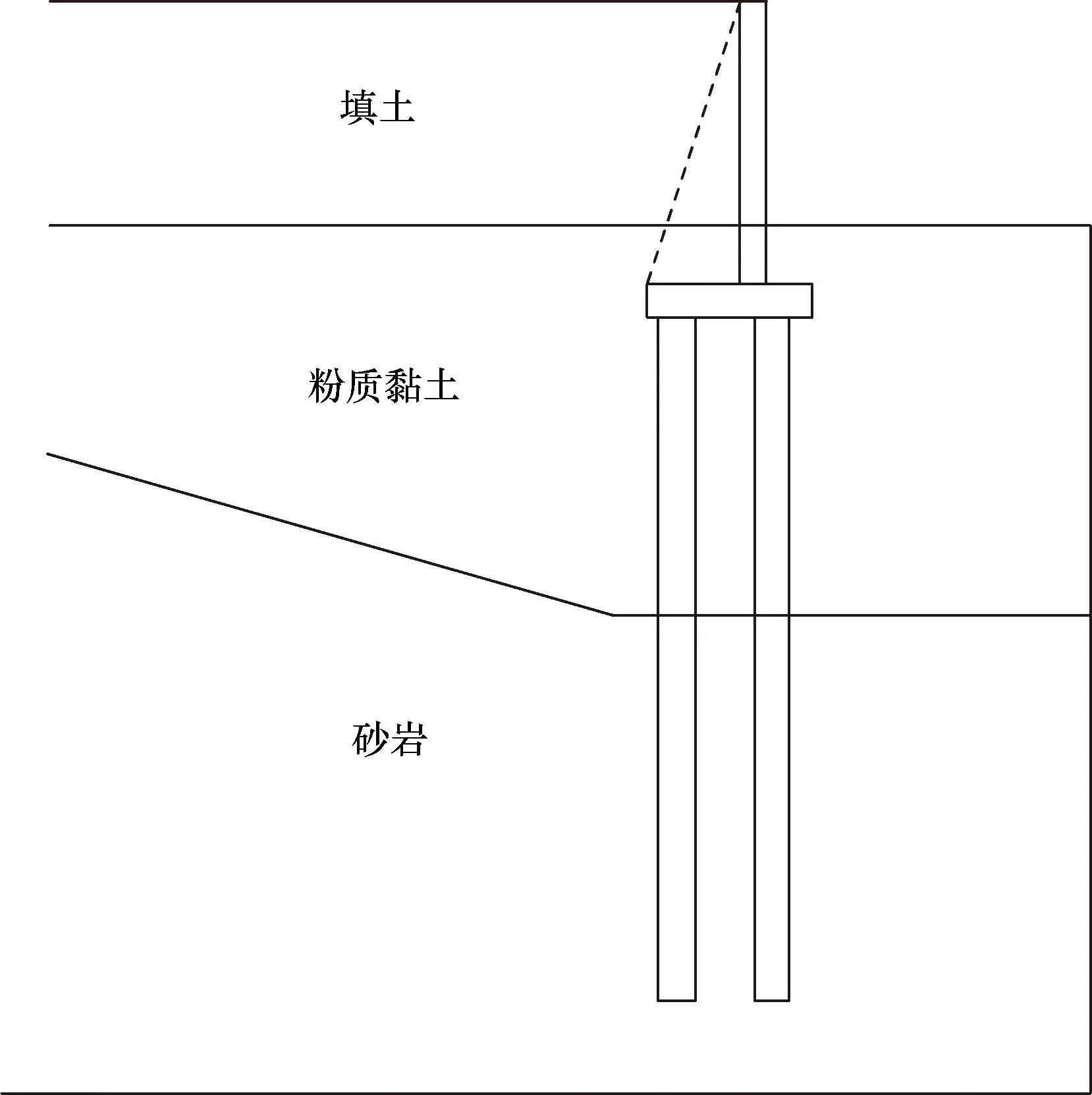
图11 支护结构所在地质断面图Fig.11 Geological section diagram of the supporting structure

最终计算得到墙背第一破裂角为32.5°,无第二破裂面存在,墙背主动土压力Ea=442.301 kN,水平方向和竖直方向土压力分别可计算为Ex=314.4 kN和Ey=311.1 kN,墙身截面积13.25 m2,重量为331.2 kN,整个墙踵上的土重214.9 kN,则可求解得到竖直方向总荷载为Nm=860 kN,计算中地基系数K取4 000 kN/m4,假定竖直方向的荷载全部由托梁承担,则可以根据连续梁法和弹性地基梁法求解得到梁弯矩和剪力的计算结果如图11、图12所示。

图12 托梁弯矩图和剪力图Fig.12 Bending moment diagram and shear force diagram of joist

从图11、图12(a)可以看出,弹性地基梁法和传统地基梁法在弯矩结果近似,不同的是,弹性地基梁法在跨中弯矩和支座弯矩处数值均小于传统地基梁法,这是源于连续梁法不考虑地基反力作用,过小的评价了托梁的承载能力,而弹性地基梁法考虑地基反力作用,将支座处视为固定端,可有效降低托梁在两端的承受力;分析两种方法计算求解得到的剪力结果可以得到类似弯矩计算结果的结论,传统连续梁剪力图(图13)为一条直线,即托梁上部荷载全部由托梁承受,导致托梁两端受到最大的剪力作用,若以传统连续梁法作为边坡防护设计依据,这是一种最保守的设计方法,会造成托梁材料的过多浪费。

图13 桩基位移图、弯矩图和剪力图Fig.13 Displacement diagram,bending moment diagram and shear force diagram of pile foundation

假设水平方向的荷载全部由桩基承担,前后排两根桩承受荷载近似看作100%、75%、50%和25%的分担比,则单根桩基受力特征可视为在桩顶受到剪力作用,桩基地基系数m取4 000 kN/m4,此时采用所提出的弹性地基梁法和传统地基梁法计算结果如图13所示。

从图13可以看出,不同分担比下,弹性地基梁理论结果显示在受到桩顶横向作用力下,桩基弯矩随桩基埋深的增加而减小,弹性地基梁法显示桩基在桩顶位置处具有最大弯矩,随后弯矩很快趋于0,剪力出现在桩顶附近,随后在地基作用下,剪力逐渐减小为0,不同分担比下,桩的位移、弯矩和剪力存在不同,表现在,当全部荷载均有桩基承担时,桩基位移最大,无论是正弯矩还是负弯矩均最大,剪力也最大,此时桩基具有较大的变形。

4 结论

在具有软弱地基的边坡治理工程当中,传统的单一支护结构难以保证边坡的安全稳定,托梁桩基挡土墙支护结构作为一种新型支档结构在该地基中具有较好的工程实用价值,现今缺乏有效的理论算法对整个结构进行计算,以某变电站填土边坡为研究对象,以有限差分原理为核心理论基础,对该种结构进行理论求解,得出以下结论。

(1)根据扶壁式挡土墙墙后土压力平衡条件,采用朗肯土压力模型,求解得到墙后土压力大小,将土压力分为水平荷载和竖直荷载,考虑墙体及土体自重,并分别作为托梁和桩基受力特征计算的输入荷载。

(2)将托梁及桩基分别视为水平方向及竖直方向弹性地基上的梁模型,基于有限差分理论,推导得到托梁及桩基在受力条件下的变形求解方法。

(3)进一步将理论应用于实际工程案例,并对比传统连续梁模型,结果表明,在计算托梁弯矩和剪力时,有限差分解均略小于连续梁解,这是因为连续梁解未考虑地基的支撑作用;在计算桩基受力特征时,后排桩靠近滑坡,承受较大的荷载,将后排桩与前排桩承受荷载的比例分为100%、75%、50%和25%进行特征量计算讨论,结果发现后排桩位移、弯矩和剪力随承受荷载的增大而增大,总体上,桩基形变量较小,边坡总体处于安全状态。