数形结合思想在初中数学教学中的应用

何朝富

一、引言

随着课程改革的深入推进,数学教学领域数形结合思想的应用受到高度关注。在教学过程,教师巧妙渗透数形结合思想,不但能够帮助学生理清知识脉络,理解数学知识的本质,而且还能提高其数学问题解决能力。因此,研究数形结合在教学实践中的应用具有现实意义。

二、数形结合思想概述

初中数学中,数形结合思想是指将数学和几何图形相结合,通过几何图形来解决数学问题的一种思想方法。这种思想方法可以帮助学生更好地理解数学概念和数学知识,提高学生的数学思维能力和几何直观能力。在初中数学教学中,数形结合思想的应用范围非常广泛,可以应用于各个数学领域,如平面几何、立体几何、三角函数等。在平面几何中,数形结合思想可以帮助学生更好地理解平面几何概念和平面几何知识,如相似三角形、勾股定理、圆的性质等。在立体几何中,数形结合思想可以帮助学生更好地理解立体几何概念和立体几何知识,如立体图形的表面积和体积、圆锥及侧面展开图等。在三角函数中,数形结合思想可以帮助学生更好地理解三角函数概念和三角函数知识,如正弦、余弦、正切等。

总之,数形结合思想是数学学科学习与解题中常见的思想方法,可以帮助学生更好地学习数学基础知识,提升解题正确率。教师在数学教学中应注重数形结合思想的应用。

三、数形结合思想在数学教学中的应用价值

新课标对于初中数学教学建议为“教学过程教师要让学生感受数学思想,积累学习经验”。在常规课堂教学环节,数学知识可以视为“明线”,直接在教材当中即可找到,而数学思想可以视为“暗线”,需要学生对于数学知识进行内化,经过总结和提炼才能获得。初中阶段,不同知识的讲解数形结合的应用方式不同。比如,在解析几何问题教学方面,数形结合的应用是将坐标法作为核心,利用图形引领学生参与代数运算,总结图形性质,辅助学生深入理解数学概念,明确数学算理知识,把握数学知识的前后联系,对于学生核心素养的培育具有重要影响。

数形结合思想的应用能够将学生思维空间拓展,对于其数学思维的培养也有促进作用。与此同时,应用数形结合可指导学生多角度感受和体验数学知识,在解决问题的时候能够灵活多变。比如,教师在函数知识讲解阶段,可以选择数形结合思想讲解函数概念,以图形作为切入点,辅助学生快速、准确掌握函数概念与性质。在数形结合应用环节,还能为学生提供诸多解题思路,在数和形转化过程提升学生形象思维与抽象思维。

整体而言,初中数学教学,数形结合应用价值体现在以下三方面:第一,具备实用性,在数学思想应用阶段,可从学生的生活情境角度出发,建立实物模型,带领学生探索数量关系,将抽象数学问题直观呈现,让学生轻松学习和记忆,调动其学习数学积极性。第二,具有辅助性,部分数学概念抽象,学生对数学知识学习和掌握相对困难,引入数形结合,辅助学生依托图形来记忆数学公式或者概念,能够满足其思维发展需求。第三,具有发展性,数形结合的应用可以将学生形象、抽象等思维紧密结合,指引学生在数形互助环境之下开拓学习思路,发展思维。因此,在初中数学教学方面,教师要积极利用数形结合辅助学生理解问题、记忆知识、寻找思路,在学生脑海当中建立完善的数学体系,促进学生思维全面发展。

四、数形结合思想在初中数学教学中的应用

(一)不断学习,强化对数学思想认识

在育人过程中,要给学生一碗水,教师必须要有一桶水。也就是说,教师本身的知识水平十分重要,需要不断提高自身对知识的认识和理解,才能做好育人工作。数学教师对于数形结合思想的认识程度决定着该思想在数学课堂当中的应用成效。当教师教学经验丰富时,能够抓住数学思想的渗透时机,根据教学需求,准确地将数形结合引入课堂。因此,教师要不断学习,丰富自身理论素养,加强阅读,重点阅读数学思想发展史相关书籍,明确数学思想的发展过程,从根源入手,对于数形结合形成深刻的认识。在课堂授课阶段,适当引入数学典故或者数学问题,向学生介绍数学思想,激发其学习兴趣,锻炼学生思维能力。

(二)研读课标,分析数形结合和数学知识联系

课标和教材是教师教学过程重要依据,其中凝练优秀教育者智慧结晶。只有教师对课标要求有正确的理解,才能明确数形结合可以在讲解哪些讲解阶段应用,有助于学生哪些素养的提升,让课堂教学目标明确,辅助学生深度学习。要做到以上几点,需要教师深入研读课标内容,对于几何直观、空间观念等关键词语有全方位了解,明确数学课程具体内容和教学建议,对于教材深入挖掘,梳理其中和数形结合思想相关的内容,才能精准应用数学思想。

例如,在“数与代数”领域,涉及如下几种数学思想:第一,数与式,其中数轴部分涉及利用数轴表示有理数;绝对值这部分内容,涉及利用数轴理解绝对值含义、相反数等;实数内容的讲解通过数轴理解数轴上的点与实数之间有一一对应关系;平方差公式讲解利用拼图方式来验证平方差公式等以上知识都反映出以形助数思想。第二,方程与不等式,在一元一次方程讲解阶段,要求学生利用线段图对等量关系进行分析,列出方程;二元一次方程和一次函数内容讲解,要求学生根据平面直角坐标系内一次函数位置关系,判断方程组解;不等式解集内容讲解,要求学生用数轴代表不等式或者不等式组解集等以上知识都反映出以形助数思想。第三,函数,利用图像表示变量关系内容讲解,要求学生观察图像,对于自变量和因变量关系进行分析;函数部分讲解,选择图像法代表函数,利用函数图像分析函数关系;一次函数图像内容讲解,根据图像对于正比例函数、一次函数之间性质和关系进行分析等以上知识点当中也反映出以形助数的思想。

(三)因材施教,尊重学生认知规律

从教育心理学角度分析,不同年级学生心理特征不同,学习特点也各不相同。七年级学生刚刚升入初中,形象思维处于主导地位;八年级学生心理和思维逐渐发展,教学过程需要教师引导,否则当学习内容过于抽象的时候,可能令学生产生畏难心理;九年级学生学习压力较大,能够利用抽象思维思考问题。在应用数形结合之前,需要教师对不同年级学生特点有全方位的了解,选择差异性教学方式。七年级学生教学,优先选择直观教学方式,辅助其理解图像概念,注重学生动手画图这项能力培养;八年级数学教学,要引导学生分别从“数”“形”角度出发,理解所学内容,感受数学图形的直观性和美观性,进而体会代数方法的精准性;九年级数学教学,教师可以将数学思想和方法系统化向学生介绍,引领学生归纳总结,鼓励其利用画图、想象等方法解决问题,对于难以用代数方法解决的问题,选择几何方法解决,培养学生逻辑推理能力,根据学生特长和优势,指导其运用数形结合方法解决问题。

(四)创设情境,感受数形结合思想

新课标明确指出,在数学教学过程当中,教师要采取多种措施,培养学生主动学习兴趣,满足其个性化发展需求。部分学生对于数形结合的应用意识薄弱,本质原因在于其对数形结合理念和特点理解不够深入,教师要反思教学情境创设是否能够满足学生需求,教学方法是否能够调动学生兴趣,教学流程设计是否科学合理,精心设计教学活动,指导学生运用数形结合思想解决问题。

例如,在讲解“平面直角坐标系”这部分内容时,教师可选择生活化情境,组织教学活动。“要求学生在课堂上将桌椅并拢,利用两根长绳(带有箭头标记)交错,将一个学生作为原点,所有学生都作为坐标点,将班级分为4个象限,相邻正坐标轴区域的学生处于第一象限内,在课堂进行游戏辅助学生认识平面直角坐标系”。以游戏活动为载体,让学生感受数形结合思想的运用。几何知识的讲解,也可以利用实物模型,为学生提供棱柱、圆柱等学具,鼓励学生探究观察,寻找事物几何性质和数量关系,积极参与数形结合活动,强化应用意识,感受数形结合思想。

(五)科学引导,辅助学生转化数学语言

在数学教学过程当中,数学语言的地位显著,具体包括字、符号、图像三种,数学语言是表示数学领域物体位置关系或者数量关系的基本形式。在教学过程中,数形结合应用即指三种语言之间的相互转化,解决数学问题。部分学生难以准确利用数学语言对于数学问题当中数量关系或者图形特点进行分析,主要原因是学生对于数形之间的表征转化能力相对较弱。事实上,不同语言的优势不同,文字语言简练精确,符号语言优雅简明,图像语言生动形象,将三种语言有机融合是学生运用数形结合关键所在。所以,在数学课堂上,教师可以重点指导学生对数学语言进行转化训练。

例如,在讲解“垂径定理”内容时,使用文字语言进行描述,为垂直圆弦的直径同时平分这条弦和其所对的弧;使用图形语言进行描述,如图1所示,使用符号语言进行描述,AB是圆O的一条弦,CD为圆O的直径,若CD垂直于AB,垂足为M,则AM和BM相等,弧AC等于弧BC,弧AD等于弧BD。通过数学语言之间的转化训练,让学生感受数学语言的简洁美和外形美,调动学生数形结合的应用热情,提高学习效率。

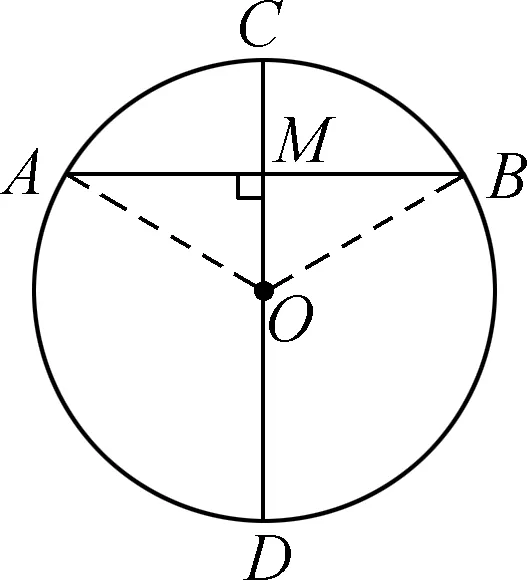
图1 垂径定理的图形表达

(六)习惯培养,应用数形结合解决问题

新课标针对初中阶段学生教学提出如下要求,“掌握图形性质、运动规律、物体位置等特点,培养学生空间观念,运用图形来思考问题,建立几何直观”。充分体现以形助数方法的运用。部分学生在运用函数图像解决不等式获得方程问题能力相对薄弱,选择的解题方法不够简洁,这种情况能够反映学生难以利用图像解决数学问题。所以,在日常教学过程当中,教师要给予学生习惯培养高度重视,让学生能够根据问题根据画图,养成认真读图和善于用图的学习习惯。

比如,针对“行程问题”的求解,要求学生使用线段图,形象直观地将速度、时间、路程之间关系呈现出来,让等量关系一目了然;针对函数问题的求解,要突破代数运算的解题思维,善于利用图形,在画图过程提取有效信息,借助图像对函数性质进行分析,梳理函数和方程、不等式之间关系,深入分析待解决问题,找到最佳解题路径。教学过程中,重点培养学生利用图形解决问题的习惯,用简单的方法或者思路解决复杂问题,感受数形结合应用能够起到化繁为简的作用,培养学生学习自信。

(七)重视基础,强化概念讲解数学思想渗透

课标对于基础知识的学习提出明确要求,部分学生对于教材当中的概念和定义学习重视度不足,认为以上内容相对简单,无须深入研读,只需要做题阶段会运用即可。事实上,数学概念和定理当中蕴含丰富的数学思想,夯实基础知识能够帮助学生更好地运用数形结合思想解决问题。

(八)全面融入,在不同课型中应用数学思想

在数学新课讲解阶段,教师可以利用数形结合思想,以直观图形辅助学生理解和学习抽象概念。在讲解新的公式和定理的时候,既要关注学生对知识结论能否习得,又要将数学知识实质呈现出来;在讲解数学概念、定理、性质和法则的时候,应用图形的直观性进行分析和讨论,让学生经历知识的生成过程,体会从具体向抽象方向发展的规律,进而对数形结合形成初步认识。

例如,在“有理数”知识学习阶段,针对相反数这一概念,教师在讲解过程可以选择数轴辅助教学,便于学生直观观察相反数特点,进而理解绝对值相同且符号不同两个数即互为相反数,将数学概念、直观图形之间建立对应关系,直观呈现数和形的关系,培养学生几何直观能力与数感能力。

在习题课教学方面,教师同样可以选择数形结合思想,先为学生讲解如何在题目中运用数形结合思想思考问题,然后实践运用。比如,实数、数轴上的点之间具有一一对应的关系,能够判断有理数大小这类问题;在一元一次方程、二元一次方程求解过程中,教师可以利用函数图像法讲解;几何问题若未给出图形,学生可以根据题意画出图形,根据图形寻找其中隐含的关系,运用正确的方法解决问题。

除此之外,在复习课上,教师也可运用数形结合思想辅助教学。比如,一次函数内容讲解以后,教师可以带领学生回顾函数定义、一次函数、正比例函数、二元一次方程等知识,总结本单元涉及的数形结合思想,在学生了解的基础上,在解决问题当中展开实际应用,提高其解决问题能力,不断完善学生的知识体系,使其通过数形结合,感受数学知识之间的联系。

五、结语

综上所述,在初中数学课堂上,教师要高度关注数形结合应用的重要性,不断学习丰富自身的知识储备,研读课标和教材,寻找数形结合的应用要点。根据学生认知规律和兴趣特点,创设课堂教学环境,让学生感受数形结合应用优势,强化学生数学语言之间转化能力,培养其读图和用图习惯,基于数学内容讲解,将数形结合思想巧妙引入课堂,提高课堂教学效率。