基于集群划分的含分散风电配电网电压调节策略
2023-07-30严玉廷
严玉廷
(云南电网有限责任公司电力科学研究院,云南 昆明 650217)
0 前言
目前,电力市场的主要发展方向是允许电网中的分布式发电用户直接与有电力需求的用户进行交易。电网企业只提供电力基础设施,并收取相应的“网络费”[1]。同时,它们还允许有能力提供辅助服务的用户参与辅助服务市场[2],并与电网企业合作维持电网稳定运行,以充分利用分布式能源,提高用户参与电力市场的灵活性。传统的集中配电网控制不再适用于具有发电、储能、功耗和辅助服务能力的多节点分布式能源网络。近年来出现的分布式能源集群为解决这一问题提供了新思路。分布式能源市场的发展也为分布式能源的消费和提高能源效率提供了良好的平台。分布式能源集群是将不同地理位置条件下的分布式能源汇集集中管理,如微电网的方式。集群通常没有实际的范围边界,它一般是根据特定的优化目标来实现的,为电网的运行和控制提供了方便,并且经常随着系统运行状态的变化而实时变化。随着电力用户参与电力市场的灵活性不断提高,分布式能源集群优化的研究也越来越多。在交易机制的研究中,提出了多种交易机制和机制下的具体交易策略。文献[3]建立了由风力发电系统、PSS 和变负荷组成的微电网仿真模型。文献[4]研究了考虑市场竞争的多微电网电力交易机制,其中以售电方为交易的引导者,并根据购电方的报价制定售电策略。文献[5]提出了一种基于光伏分布式发电和电池储能系统的微电网P2P能量交易模型。文献[6]设计了一个P2P 能源交易平台,并利用博弈论模拟P2P 能源交易,以改善当地能源生产和消费之间的平衡。文献[7]介绍了一种基于光伏能源净价格的Stackelberg博弈方法,并提出了提前一小时的最优定价模型,以协调光伏能源的共享和自身利润的最大化。文献[8]考虑了风速和太阳辐射通量的不确定性,结合联盟博弈论、DG 单元和CRPSO 优化算法的优点,以最小化负荷利用率和供电成本。文献[9-10] 以光伏用户群为研究对象,考虑需求侧响应的影响。基于博弈论设计的能源交易机制,能够充分考虑现实中双方决策的相互影响,实现自身利益的最大化。
随着电力用户参与电力市场的灵活性不断提高,分布式能源集群优化的研究也越来越多。在增加市场参与者收入方面,电力市场中分布式发电的净价通常低于电网销售的购电价格。基于允许用户独立交易的市场,划分适当的集群,并建立合理的定价机制,在内部进行电能交易,这将使电力购买者和销售者都受益[7-12]。在电压控制优化方面,随着分布式电源接入的增加,原有的电压调节控制策略利用集群内的自治特性优化集群内的电压控制[13-21]。在减少功率损耗方面,用户之间的主动和独立事务在本地传输。与分布式发电的“自给自足+ 盈余上网”交易机制相比,电力损耗更大[22-23]。将差异较大的输出特性曲线划分为同一簇,使集成簇的输出趋于平滑,有效缓解分布式发电接入对电网运行的影响[24]。
综上,大多数分布式能源集群优化研究没有考虑不同时间尺度下的用户负荷和发电量。特别是风能、光能等可再生能源的产量预测精度对集群划分的影响。未考虑有功功率变化对电压调节的影响;大多数研究集中于分布式发电的无功调节,而对其他类型的分布式能源,如储能装置、电动汽车等的电压调节能力关注较少。本文考虑大规模分布式能源的接入,充分利用分布式能源的调压能力,将分布式能源无功调节作为优先调压手段,尽可能满足电力用户的用电体验。所提出的电压调节方法具有很高的调节效率。在集群划分方面,集群划分模式对分布式能源的接入和网络运行状态的变化具有很强的适应性。可根据需要实时改变集群划分方式,以达到更好的集群调压效果。
1 分散式风电电压调节与潮流计算模型
1.1 分散式风电电压调节模型
目前,双馈感应发电机(DFIG)已成为风力发电机的主流机型。它可以实现有功和无功功率的独立控制,具有灵活的功率控制能力。DFIG 网侧变流器调节范围[25]。
其中,Qg是DFIG 网侧变流器的无功功率调整值;Ps是定子的输出有功功率,即风电的有功输出;Sgmax是电网侧变流器的容量;s是DFIG 的滑移率。
1.2 潮流计算模型
潮流计算模型为了根据每个分散风电节点的功率变化快速计算出每个节点的电压,加快优化速度,采用修正方程更新电压来代替传统的潮流计算。具体计算过程如下:
展开上述公式:
消元后得:
其中,ΔP,ΔQ,Δθ和ΔU分别为节点有功功率、无功功率、电压相角和电压幅值的变化;H、N、J、L 为雅可比矩阵元;SP是电压有功功率灵敏度矩阵,矩阵中的元素SPij表示节点j注入有功功率的变化对节点电压变化的影响程度;SO是电压无功灵敏度矩阵,矩阵中的元素SOij表示节点j注入无功功率的变化对节点电压i变化的影响程度。潮流计算时间比计算修正方程和更新电压的时间长得多,可以大大提高调压效率。
因此,有以下公式:
基于上述两个特征,节点之间的电气距离可定义为以下公式:
其中,n是网络中所有节点的数目。Lij表示节点i和节点j之间的电气距离。
1.3 分区方法
本文基于市场交易模式下电压调节模式的聚类划分,以电气距离为依据进行聚类划分,以K 均值聚类算法为划分方法。该算法在经典K-means 算法的基础上进行优化,以最小化簇内节点到簇中心距离的平方和。因此,电压调节分散风电集群划分的目标函数如下:
其中,Ljεi是节点j到簇中心的距离εi,|Ci|表示簇i中的样本数。
为了优化电压调节的聚类划分,本文在经典K 均值聚类算法的基础上,对初始聚类中心的选择、聚类中心的更新和聚类数K 值的选择进行了优化。
初始聚类中心的选择往往是决定聚类结果质量的标准之一。初始聚类中心选择不当容易使K-means 聚类算法陷入局部最优。在本文中,我们指定初始聚类中心以避免不稳定的划分结果和局部最优结果。对于聚类中心的初始化,首先根据节点周围的密度定义节点索引,然后根据尽可能分散初始聚类中心的原则,在高索引节点中选择聚类中心。具体步骤如下:
1)对于每个节点i,计算其与所有其他节点之间的距离,如下式所示:
2)计算节点索引:设置参数M,将元素从节点i的i开始按升序排列在LSi中。索引i 可以表征节点i 周围的节点密度。节点i 周围的节点越多,距离第M个最近的节点越近,即索引距离越小。
3)选择高索引节点:设置集合T,按从小到大的升序排列index={index1, index2, ...,indexN} 中的元素,并选择排序后的第Tth个元素的值作为阈值。索引小于阈值的节点属于高索引节点。索引越小,节点周围的节点越多,成为集群中心的可能性越大。因此,确定高索引节点集,并从该集确定集群中心。所选的高索引节点集为Hindex={index1, index2, ...,indexT},并在这些节点中选择初始聚类中心,以避免在边缘节点上选择初始聚类中心的情况。
4)选择第一个簇中心:选择节点索引最高的节点作为第一个簇中心εi。
5)选择其他k-1 群集中心:在集合中的其余节点中,选择远离所有群集中心的节点作为下一个群集中心。如下式所示:
其中,i表示删除所有在Hindex 中选择为集群中心的节点号。
1.4 集群中心更新
由于电距离表征了样本之间的相似性度量,因此不可能计算每个聚类中所有样本特征的平均值作为新的聚类中心。在本文中,将新形成的簇中与其他节点距离之和最小的节点作为新的簇中心,如下式所示:
其中,εk表示k 簇的簇中心。
聚类数K的大小往往影响聚类结果的质量,因此需要定量指标来客观评价K 值对聚类划分的影响。本文以每个簇的内部节点与簇中心之间距离的平方和作为评价簇划分结果的指标(平方误差之和,SSE),如下式所示:
K0是整个图像的拐点。K0之前,SSE 随K的增大而减小,且减小速度较快;K0后,K 的增加对SSE 的降低影响不大。因此,K0可以确定为最佳聚类数K。此时,不仅聚类结果尽可能优化,而且聚类数也不会太大。基于电压调节的集群划分过程如图1 所示。

图1 基于电压调节的集群划分流程图
当簇数的K值越大,每个簇中的节点数越少,每个节点离簇中心越近,距离平方和越小,即指数SSE 随K的增加单调减小。这也意味着簇划分结果更好,如图2 所示。然而,对于配电网的电压调节,集群K 的数量不应太多,否则集群中的节点数量太少,会降低集群中电压调节辅助服务的灵活性。

图2 聚类划分指数SSE与聚类数K的关系
2 集群电压调节模型
分散式风电电压调节策略的研究主要是解决分散式风电大量接入配电网引起的电压超限问题。电压调节方式主要采用分散风电各节点的有功和无功功率调节。在电压越限的背景下,有功功率输出的降低和无功功率的吸收是主要因素。为了保证分散风电的有效利用,尽可能提高电压质量,在控制电压越限的基础上,尽可能减少电压波动和功率调节,进行电压调节。本文以最小化功率变化和电压偏差为优化目标,以最严重的电压超限幅值与电压调节要求V 之间的差值作为惩罚函数。在满足约束条件的基础上,实现了集群内部的电压调节。
2.1 目标函数
划分的基础聚类划分的最初目的是根据某个特征将相似的个体划分为同一个聚类。本文中集群划分的目标是电压控制。根据电压对功率变化的敏感性,将互敏度高的划分为同一簇,互敏度弱的划分为不同簇。因此,电压调节策略可以在集群内有效实施,对集群外部影响较小。分布式能源网络中的有功和无功功率对节点电压有影响,不同节点之间的电压效应明显不同。初步考虑利用节点注入功率的变化对其他节点的影响来定义电气距离。
其中,f1表示集群内电压调节产生的总功率变化量,M表示集群内所有分散的风电节点数,ΔPi表示节点i产生的有功功率减少量,ΔQi表示节点i产生的无功功率吸收量。f2表示f1之间的最大偏差,集群内的电压波动越小,电压质量越好。N表示集群中所有节点的数量,Vi表示节点i的电压幅值,Vneed表示电压调节所需的电压幅值。f3是一个惩罚函数,表示集群中电压超过极限的程度。将其作为惩罚函数加入到目标函数中,通过调整惩罚因子可以达到良好的电压调节效果。f是目标函数,λ1和λ2分别是f1和f2的权重系数。C是惩罚函数f3的惩罚因子。
电压质量是需要满足的电气要求。然而,降低有功功率输出也会在一定程度上损害用户的功耗体验。因此,在电压调节中,通常优先考虑吸收无功功率进行电压调节。当无功电压调节不能满足电压调节要求时,则降低有功功率输出以实施电压控制。因此,改进了目标函数f1:
当首先执行吸收无功电压调节时,等式(16)用作目标函数。当无功功率调节不能满足电压调节要求时,将等式(12)用作目标函数。
2.2 约束条件
作为变量ΔPi、ΔQi在电压调节策略中,由于分散风电调节能力的限制,不可能无限期增加。各类分散风电都有自己的无功调节能力,各类分散发电的有功功率削减不能超过现有有功功率输出范围,并根据电压越限情况下的电压控制,规定各节点的有功功率削减和无功吸收为正,避免节点间反向调压,导致调压结果偏差。因此,变量存在约束ΔPi、ΔQi,如下所示:
整后,集群内的电压控制在标准范围内,因此配电网电压被限制在限值以下,如下所示:
2.3 求解算法
基于以上分析,基于粒子群优化算法实现了集群的电压控制。主要步骤如下:
1)确定PSO 算法中的参数:粒子数Nv、学习因子C1,C2、惯性权重ω、迭代次数l。
2)首先,将无功功率调节作为集群电压调节的电压调节手段,以{ΔQ1, ΔQ2,..., ΔQM} 作为可调变量(优化问题的变量),方程为(14-16)作为相关函数。
3)初始化Nv粒子的位置和速度。
4)计算并存储pbest和gbest的值。
5)使用以下公式更新粒子速度和位置。
6)计算每个粒子的适应度函数值,并将其与自身的最佳位置Pbest进行比较,以选择更新后的Pbest。
7)比较所有Pbest并更新gbest。
8)检查是否已达到最大迭代次数。如果没有,重复步骤5);如果达到最大迭代次数,请执行步骤9)。
9)检查电压质量是否符合要求。如果是,则输出集群中每个节点的电压和每个分布式能源节点的无功调节;如果不满足,则采用有功功率降低和无功功率吸收进行联合调节,即以{ΔQ1, ΔQ2,..., ΔQM, ΔP1, ΔP2,..., ΔPM}作为可调变量(优化问题的变量)。
10)重复步骤3)-8)。当达到最大迭代次数时,检查电压是否符合要求。如果是,则输出集群中每个节点的电压、每个分布式能源节点的无功功率调节和有功功率降低;如果没有,请向其他集群寻求电压调节服务。
由于粒子群优化算法适用于无约束优化问题,且簇内电压调节存在可变约束;而对于基本的粒子群优化算法,如果不采取一些限速措施,很容易使更新速度过大,粒子不收敛。因此,需要对算法进行优化。
1.初始粒子群选择的优化,粒子群算法的初始化选择。
优化通常是在空间中随机选择的。由于集群中的电压调节变量有上限和下限,因此此处记录为xmax、xmin;为了防止算法不收敛,粒子的速度受到限制,此处记录为vmax、vmin。因此,初始粒子的随机选择优化如下:
其中,r是介于0 和1 之间的随机数。优化后的初始粒子更新可以有效地防止初始变量越过边界。
2.粒子群位置和速度更新的优化。由于变量有上限和下限,因此每次更新粒子位置时,都应将其与时间上的有限范围进行比较。当粒子群越过边界时,强制指定相应的变量或速度作为边界值,使粒子群能够在有效范围内搜索最优解并快速收敛。
为了根据每个分布式能量节点的功率变化快速计算集群中每个节点的电压,加快优化速度,采用修正方程更新电压来代替传统的潮流计算。
3 算例分析
为参数设置示例本文以IEEE33 节点模型为仿真实例,验证了所提出的集群划分方法对市场模式下分布式能源网络电压调节的优化效果。计算示例的系统图如图3 所示:
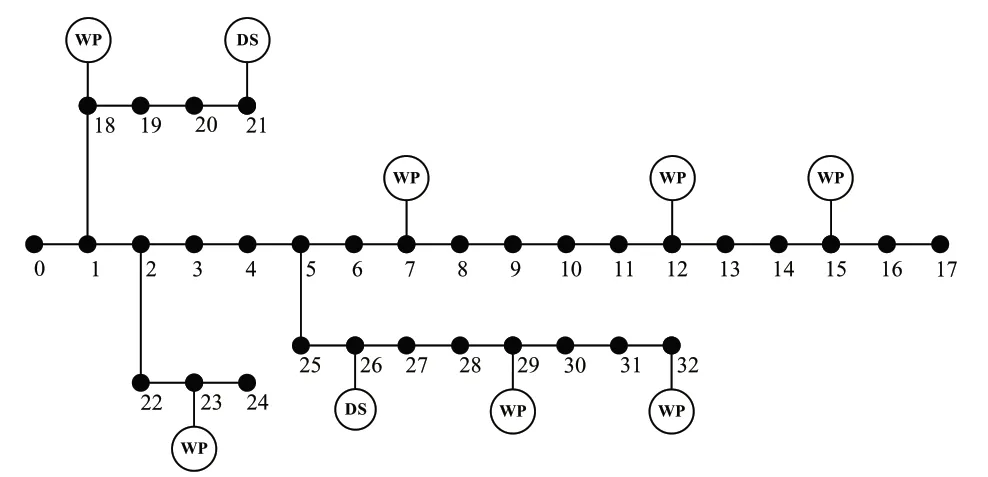
图3 IEEE33节点系统图
节点0 是系统与电网的连接点,共有9 个分布式能源接入点,其中在节点7、12、15、18、23、29 和32 添加分布式风电,在节点21和26 添加储能设备。各节点分布式能量24 小时输出曲线如图4 所示。

图4 布式能源输出曲线和全网负荷曲线
选择t=12 时的场景数据进行群集划分。本文提出的优化K-means 聚类划分算法用于划分除节点0 连接到网格外的其余32 个节点。首先,利用t=12 时刻的功率输出数据和系统参数计算雅可比矩阵,并根据电距离定义生成节点电距离矩阵。其中,每个节点与节点0 之间的电气距离如图5 所示。

图5 各节点到节点0 电气距离
每个节点与节点0 之间的电气距离与实际网络拓扑中节点的相对位置距离呈正相关。距离较远的节点与节点0 的电气距离也较大。这表明,定义的电气距离可以很好地表示节点距离,是一种有效的聚类相似性度量。
将电气距离作为相似性度量,设置参数m=15 和T=15,以将示例划分为多个簇。不同K值下的聚类分割结果指数SSE 如图6 所示,这与前文中提到的聚类分割数K 的分割指数的趋势一致。
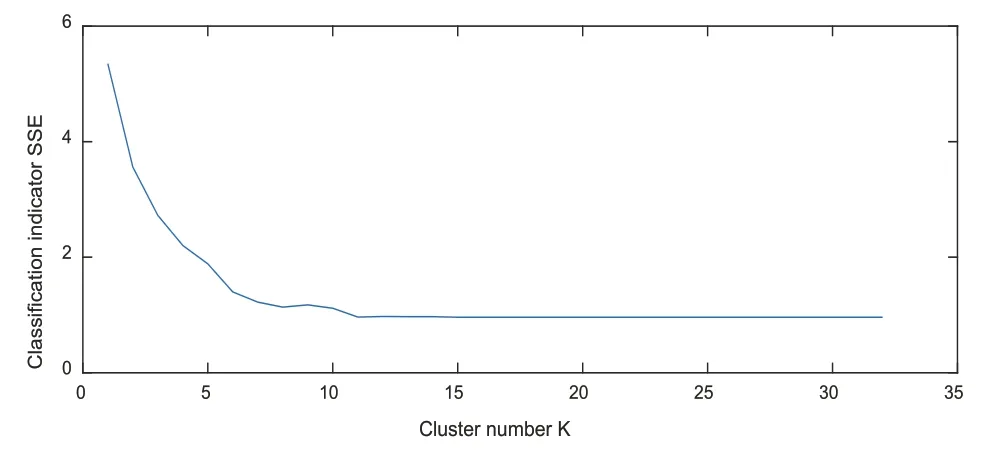
图6 不同K值下分配指数SSE的变化曲线
可以看出,当K≥6 时,增加聚类数K对指数SSE 的影响程度显著降低,此时进一步增加聚类数K并不显著,因此,可以选择最佳聚类数为6。同时,可获得K=6 的最佳聚类划分结果,如表2 所示。此时,其聚类划分指数SSE为1.4118,对应的系统图如图7 所示。

图7 K=6时系统的群集划分图
采用基于聚类的全网电压调节策略对系统电压进行调节,并在PSO 算法中设定参数:C1=C2=2,w=0.8,NP=40,I=1000;在目标函数中:λ1=1、λ2=100、c=2000。基于聚类的全网电压调节策略调节的系统电压如图8 所示,每个节点的电压幅值如图9 所示。除电网节点0外,最大节点电压为节点10,电压幅值为1.0597。

图11 大规模分布式能源接入对节点电压的影响
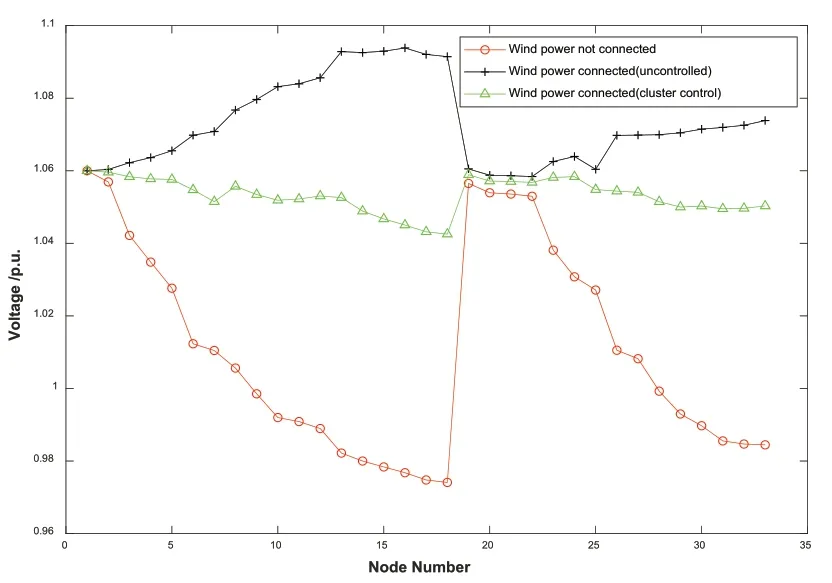
图12 集群调压后各节点电压
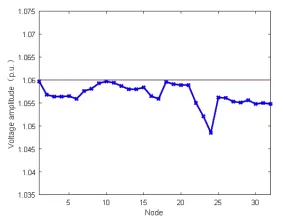
图13 集群调压后节点电压幅值
由于网络中分布式能源接入量大,电压调节能力充足,两种电压调节都可以通过无功功率调节来满足电压调节要求,而不涉及有功功率的降低。可以明显看出,在全网调压的情况下,一些节点甚至会向电网输送无功功率,这与解决全网电压超限问题的目标背道而驰,而集群式调压可以快速有效地实现调压,获得更好的调压质量。
电压调节的仿真结果也符合理论:电压在集群内进行调节,电气距离较近的节点以电压调节为主,可以大大减少电压调节的功率变化;由于节点数量多,且同时进行优化计算,整体电压调节难以收敛到最优解。
4 结束语
本文采用聚类划分方法对模型进行聚类,验证了基于分布式能量聚类的电压调节策略的优化效果,并将结果与整体电压调节进行了比较。结果表明,基于分布式能源集群的电压调节比整体电压调节具有更好的电压调节效果,在解决电压超限问题上具有更好的优势。然而,需要手动确定使用有功功率降低进行电压调节和使用无功功率进行电压调节的优先级。如果无功电压调节不满足要求,算法无法自动完成优先级任务。此外,集群之间的电压辅助服务交易还没有明确的交易机制。在聚类划分方面,聚类数K值的选择仍然需要人工选择,这大大降低了划分的效率,需要在后续研究中进一步改进。
