植草沟曼宁粗糙系数变化特征及影响因素
2023-07-29王建龙孙铮夏旭王文海吴学蕾
王建龙,孙铮,夏旭,3,王文海,吴学蕾
1.城市雨水系统与水环境教育部重点实验室, 北京建筑大学
2.北京节能减排与城乡可持续发展省部共建协同创新中心, 北京建筑大学
3.悉地(苏州)勘察设计顾问有限公司
4.北京市建筑设计研究院有限公司
植草沟是应用较广泛的低影响开发(LID)设施之一[1-3],具有传输和净化雨水径流的双重功能,可代替场地源头雨水管网传输雨水径流[4-6]。关于植草沟水量、水质控制效果已开展了大量研究,如张炜等[7]研究了植草沟恒定进水条件下,进水流量(Q进)为1~4 m3/h 时的水文特征,发现植草沟沿程流量逐渐降低,且随着进水水力负荷的减小,植草沟对雨水径流峰值和径流总量的控制效果呈上升趋势;王龙涛等[8]研究了不同水力负荷条件下渗滤型和表流型植草沟对城市地表径流净化效果的影响,发现二者对总氮的去除率分别为35.53%±10.89%、27.07%±9.88%,对总悬浮物(TSS)和总磷的去除率均高于60%;张潇月[9]研究表明,恒定进水条件下,Q进为1、2 和4 m3/h 时,植草沟对TSS 去除率为24.22%~89.95%,负荷削减率为43.36%~90.89%。因此,植草沟具有较好的雨水径流总量以及径流污染削减效果。
谢才公式是仅适用于明渠均匀流计算的公式[10-11],由于其形式简单、计算方便,在水力学、河流动力学等领域沿用至今[12]。目前植草沟沿程流量的计算一般采用谢才公式[13],但植草沟具有渗透性,存在沿程流量衰减,加之植被高度在径流冲刷作用下会发生变化,导致沿程曼宁粗糙系数(n)发生变化,且在《海绵城市建设技术指南——低影响开发雨水系统构建》中只给出了n取值范围(0.2~0.3)[14],工程设计取值时往往存在一定主观性。因此,采用谢才公式计算植草沟的沿程流量时,会存在较大的误差[15]。
近年来,国内外围绕植被对n的影响以及植草沟入渗量计算方法等开展了系列研究。在植草沟n的计算方法及其与阻力系数(CD)的关系方面,Ye 等[16]通过对n进行统计分析,建立了计算n的公式,表明n随着水深和植被的变化而动态变化,使用动态n可以有效提高水文模型中水流模拟的精度;Yusof 等[17]为了确定明渠中的流动阻力,使用天然的柔性植被(牛草)在淹没条件下评估了n以及阻力系数,结果表明n和阻力系数随着平均流速的增加而下降。同时,n和阻力系数存在较强的相关性。当前关于植草沟n的变化特征研究,主要以不同植被类型、不同Q进的影响为主。如Mailapalli 等[18]研究了裸地和耕地2 种植被类型的沟渠在不同灌溉条件下n的变化,结果表明随着时间的增加,裸地和耕地类型沟渠的n逐渐下降,且耕地类型沟渠的n高于裸地类型沟渠;Kamali 等[19]评估了2 种Q进(0.29 和0.44 L/s)条件下,植草沟n的变化情况,还评估了多级优化和SIPAR-ID 模型在计算植草沟n和入渗方程参数方面的准确性,结果表明n随流动距离的增加而增加,且在计算入渗量时,多级优化方法的平均误差较小;朱钰等[20]通过室内模型试验,研究了不同Q进时植草沟与混凝土边沟的水力特性,结果表明对于糙率相同的沟渠,流速的增大会引起n的减小。
综上所述,随着植草沟内水深以及植被参数的变化,n将发生改变,目前关于n的变化特征研究主要围绕植被种类、灌溉频率等对植草沟排水效果的影响,而关于植草沟n的取值对计算植草沟内沿程流量(Q)变化的影响,以及在变流量进水条件下n的动态演变特征,尚缺乏系统研究。笔者系统研究了不同恒定流量和变流量进水条件下n的动态变化特征,还研究了植草沟植被高度对n的影响,以期为植草沟的水力计算提供依据。
1 试验方法
1.1 试验装置
植草沟试验装置由进水箱、出水箱,进水管、回流管和植草沟组成,如图1 所示,尺寸(L×B×H)为20 m×1 m×0.5 m,纵坡为2%,断面形状为圆弧形。植草沟内所填土壤为砂土,种植植物为假俭草,植被覆盖率为100%。从进水口至出水口等间距设4 道薄壁三角堰,间距为5 m,堰底与植草沟断面形状贴合,呈圆弧形。由于试验过程中植草沟内水深较浅,堰前后断面的水深变化无显著差异,因此,堰对于沿程实测流量的影响可忽略。

图1 植草沟试验装置Fig.1 Experiment device of grass swale
试验时采用进水泵(65WQK25-15-2.2)将水输送至进水槽,进水采用电磁流量计(RZYLDG,DN50)计量流量,进水槽中的水溢流进入植草沟,经植草沟传输后溢流至出水箱,当出水箱液位达到一定高度时,由液位计(QDY70A-JX)控制循环泵(65WQK20-10-1.5)的启动,将水回流至进水箱实现水循环。
1.2 试验方案
试验包括模拟不同恒定流量、不同变流量进水条件下植草沟n变化特征,以及不同植被高度对植草沟n的影响3 个工况,不同工况下试验间隔均为2 d,以确保植草沟内土壤的初始含水率保持一致。
(1)恒定流量进水
恒定流量进水分别采用Q进为1、1.5、2、3、4 m3/h,由于Q进较小时,植草沟内Q到达稳定需要的时间较长,当Q进为1 m3/h 时,进水时间为60 min,以保证植草沟沿程渗透性能趋于稳定;其他恒定流量进水条件下,进水时间为40 min。植草沟内植被高度为23 cm。
(2)变流量进水
植草沟的汇水面积为50 m2,变流量进水分别采用降雨重现期(P)为0.33、2、5、10、20 a 降雨产生的径流量,降雨历时为60 min,进水时间均为60 min,采用芝加哥雨型,植草沟内植被高度为23 cm。植草沟的Q进过程线如图2 所示。

图2 不同降雨重现期条件下植草沟进水流量过程线Fig.2 Inflow hydrograph of grass swale under different rainfall return periods
(3)植被高度
试验设置的植被高度分别为1、15、23 cm,研究了降雨重现期分别为2、5、10 a 时不同植被高度条件下n的沿程变化规律,降雨历时均为60 min,植草沟汇水面积为50 m2。
1.3 流量监测方法
植草沟沿程流量监测采用薄壁堰[21],其尺寸及监测原理如图3 所示。堰板前端设有直径为8 mm 的连接孔,采用透明橡胶管穿过植草沟土壤层连接到植草沟侧壁,并用钢尺将橡胶管垂直固定,使用激光水准仪(DELIXI H1V2D)确定三角堰口最低点高程,作为堰上水头的0 点。在距离进水端5、10、15、20 m 处(即出水口位置)分别设置堰。从图3 可知,植草沟堰上水头高度(h)=h3-△h-0.02,其中,为减小三角堰对过流的影响,三角堰最低点距离植草沟沟底设计为0.02 m,△h=h2-h1。堰过流流量的标定方法如下:通过安装在进水管上的电磁流量计测量Q进,并同步测量进水口处的堰上水头,从而得出不同Q进条件下对应的h,结果如图4 所示。通过对数据进行拟合,可得到Q进与h关系公式如下:

图3 堰上水头计算方法示意Fig.3 Calculating method of water head on weir
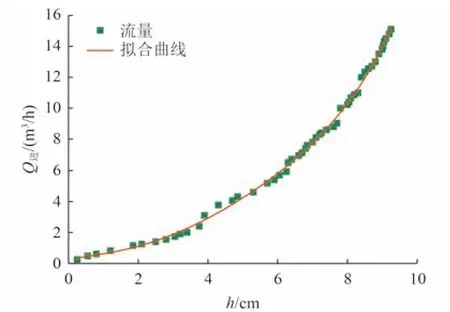
图4 堰上水头与进水流量关系曲线Fig.4 Relationship between flow rate and water head on weir
由图4 可知,式(1)具有较好的拟合精度,其中R2=0.998 1,可根据式(1)求出任意h对应的Q进。
1.4 谢才公式计算方法
植草沟沿程流量通常采用谢才公式计算,其表达式为:
式中:v为流速,m/s;R为横断面的水力半径,m;i为植草沟的纵向坡度,本研究取2%;C为谢才系数。
采用v=Q/A代替式(2)中v,因此式(2)又可以表达为:
式中:Q为植草沟沿程流量,m3/s;A为横断面面积,m2。
式(4)中,n的取值与植草沟中植被类型、曲折程度等多个因素有关,n的计算公式[22]如下:
式中:n0为与植草沟渗透材料有关的系数;n1为反映植草沟不规则程度的系数;n2为反映植草沟断面变化的系数;n3为与植草沟堰或污染物拦截设置有关的系数;n4为与植草沟植物种植有关的系数;m5为反映植草沟曲折程度的系数。n0~n4、m5的取值依据参考Cowan[22]的研究:由于植草沟的介质为土壤,故n0取0.020;植草沟形状规则,n1取0;植草沟断面变化程度较小,n2取0;植草沟内设4 道堰,n3取0.06;植被对沿程流量的影响主要取决于n4,植草沟内植被密度较高,n4取0.09;植草沟纵向无弯曲,故m5取1。将各系数带入式(5)得到n=(0.020+0+0+0.06+0.09)×1=0.17。
植草沟顶宽为1 m,断面形状为圆弧(r=0.625 m),图5 为植草沟的剖面示意。植草沟内的水位高度为H时,根据勾股定理得:
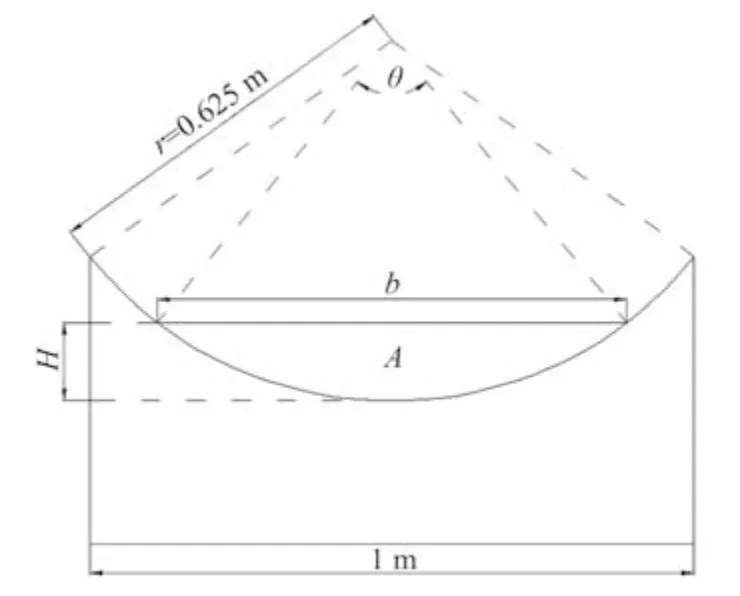
图5 植草沟剖面尺寸示意Fig.5 Sectional dimensions of grass swale
式中b为植草沟水面宽度,m。
由图5 可知:
式中θ为植草沟液面对应圆弧角度。
当水位高度为H时的湿周(X)计算公式如下:
横断面面积(A)可由下式计算:
横断面水力半径(R)可由下式计算:
综上所述,通过试验测得植草沟各沿程位置的H,结合植草沟的宽度和断面形状,可计算得出A和R,将i及算得的A、R和n代入式(4),即可计算植草沟沿程的理论流量。
2 结果与讨论
2.1 恒定流量进水条件下植草沟曼宁粗糙系数变化特征
不同Q进条件下,植草沟沿程实测流量和理论流量〔由式(4)计算的流量〕变化如图6 所示。从图6 可知,不同Q进条件下,植草沟沿程实测流量均呈现逐渐降低的变化趋势,当Q进为1、1.5、2、3、4 m3/h 时,实测出水流量分别为0.53、0.81、1.21、2.07、2.83 m3/h,其沿程流量削减量分别为0.47、0.69、0.79、0.93、1.17 m3/h,随进水流量的增大而增大。分析其原因是Q进增大后,植草沟内水深增加,进而导致湿周和渗流水头增大,植草沟内的沿程流量削减量也随之增加。同时,上述不同Q进条件下,距进水口5 m 处实测流量与理论流量的差值分别为0.43、0.36、0.24、0.09、0.38 m3/h,出水口处(距进水口20 m)流量差值分别为0.44、0.46、0.39、0.14、0.12 m3/h。可见,植草沟沿程实测流量与理论流量的差值均较大,并且随着Q进的增加,实测值与理论值之间的差值减小。分析原因主要是在不同恒定Q进条件下,植草沟内的水深均小于植被高度,当Q进较小时流速也较低,渗透所致沿程流量损失占比较大。因此,采用谢才公式计算植草沟沿程流量存在较大误差。

图6 植草沟沿程实测流量和理论流量Fig.6 Monitored and theoretical calculated flow rates along grass swale
为了进一步说明实测值与理论值的误差大小,采用纳什效率系数(NSE)以及决定系数(R2)对误差进行量化分析,NSE 和R2越接近1,说明理论值与实测值的拟合效果越好,误差越小[23-24]。当Q进为1、1.5、2、3、4 m3/h 时,NSE 分别为-6.8、0.25、0.88、0.99、0.97,R2均为0.99。由于式(4)中的横断面面积、水力半径以及植草沟的纵向坡度都是实测值,而n是根据植草沟中植被类型、曲折程度等因素进行取值(n=0.17),由此可知,n取值的偏差是导致实测值与理论值存在误差的主要因素。同时n随Q进变化而变化,当Q进较小时,植被的阻力较小,n也较低,因此当Q进<1.5 m3/h 时,n取值偏大是导致理论值与实测值存在较大误差的原因。
不同恒定Q进下,植草沟沿程流量以及n的变化如图7 所示。由图7(a)可知,在Q进相同条件下,植草沟内沿程流量逐渐降低;Q进从1 m3/h 增至4 m3/h,植草沟沿程流量均随Q进增大而增大,植草沟出水口流量由0.53 m3/h 增至2.83 m3/h,出水口流量小于Q进主要是由植草沟沿程渗透损失引起。随着Q进的增大,沿程渗透损失率(渗透流量与Q进比值)减小,该结果与沈子欣等[25]的研究结果一致。

图7 植草沟内沿程流量和n 变化Fig.7 Changes of flow rate and Manning roughness coefficient along grass swale
由图7(b)可知,植草沟内n呈沿程逐渐降低的变化趋势,随着Q进由1 m3/h 增至4 m3/h,入口处的n由0.10 逐渐增至0.20,出水口处的n由0.03 逐渐增至0.18;此外,在Q进相同条件下,n呈现沿程衰减的变化趋势。分析其原因,植草沟内水深呈现沿程衰减的趋势,且水深均远小于植被高度(23 cm),随着水深的减小,植草沟的过流断面面积减小,与植被的接触面积减少,进而导致阻水面积减小,因此出现n沿程降低的现象。Zhang 等[26]研究了植被对于泛洪区水流的影响,设置了7 种坡度和4 种倾斜角度,结果表明,当坡度为0%时,在相同的倾斜角下,n随着水深的增加,呈现先增加后降低的变化趋势,与本试验的研究结果一致。
为了进一步描述植草沟沿程n的动态演变过程,采用式(11)计算不同Q进条件下,植草沟沿程n衰减率(η),结果如表1 所示。各恒定Q进下,随着植草沟沿程距离的增大,n衰减率逐渐增大,当Q进为1 m3/h 时,n衰减率由5 m 处的19.7% 逐渐增至20 m 处的71.5%,即n衰减率呈沿程增加的趋势;但随着Q进从1 m3/h 增至4 m3/h 时,n衰减率由5 m 处的19.7%降至3.7%。可见,随着Q进的增大,n衰减率呈沿程减小趋势。
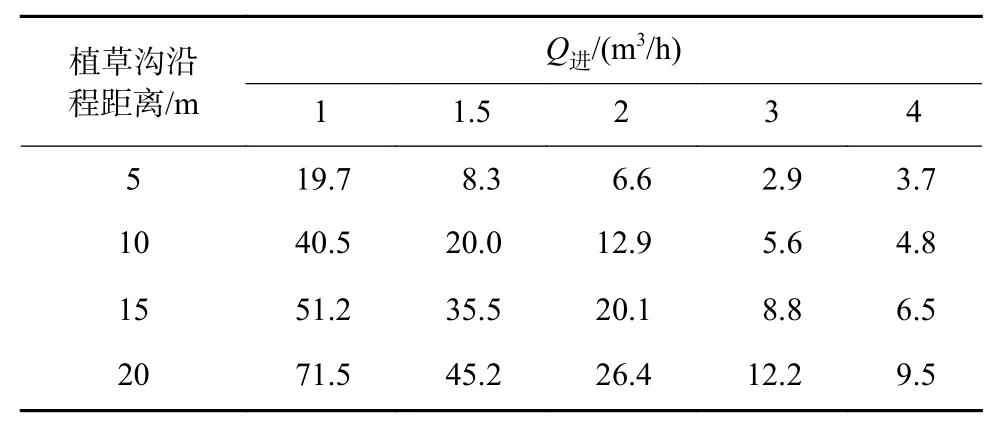
表1 不同恒定Q进下植草沟沿程n 衰减率Table 1 Manning roughness coefficient attenuation rate along grass swale under different constant inflow rates%
式中: η为n沿程衰减率,%;na为植草沟进水口处的n;nb为植草沟沿程b米处的n。
2.2 变流量进水条件下植草沟曼宁粗糙系数变化特征
将不同Q进条件下植草沟内沿程不同距离处的水深代入式(3)中,即可得到不同距离处的n。各距离处的n与降雨时间关系曲线如图8 所示。由图8可知,沿程不同距离的n均随沿程距离的增加呈现先增加后降低的趋势,且Q进越大,n越大,其最大值为0.22。
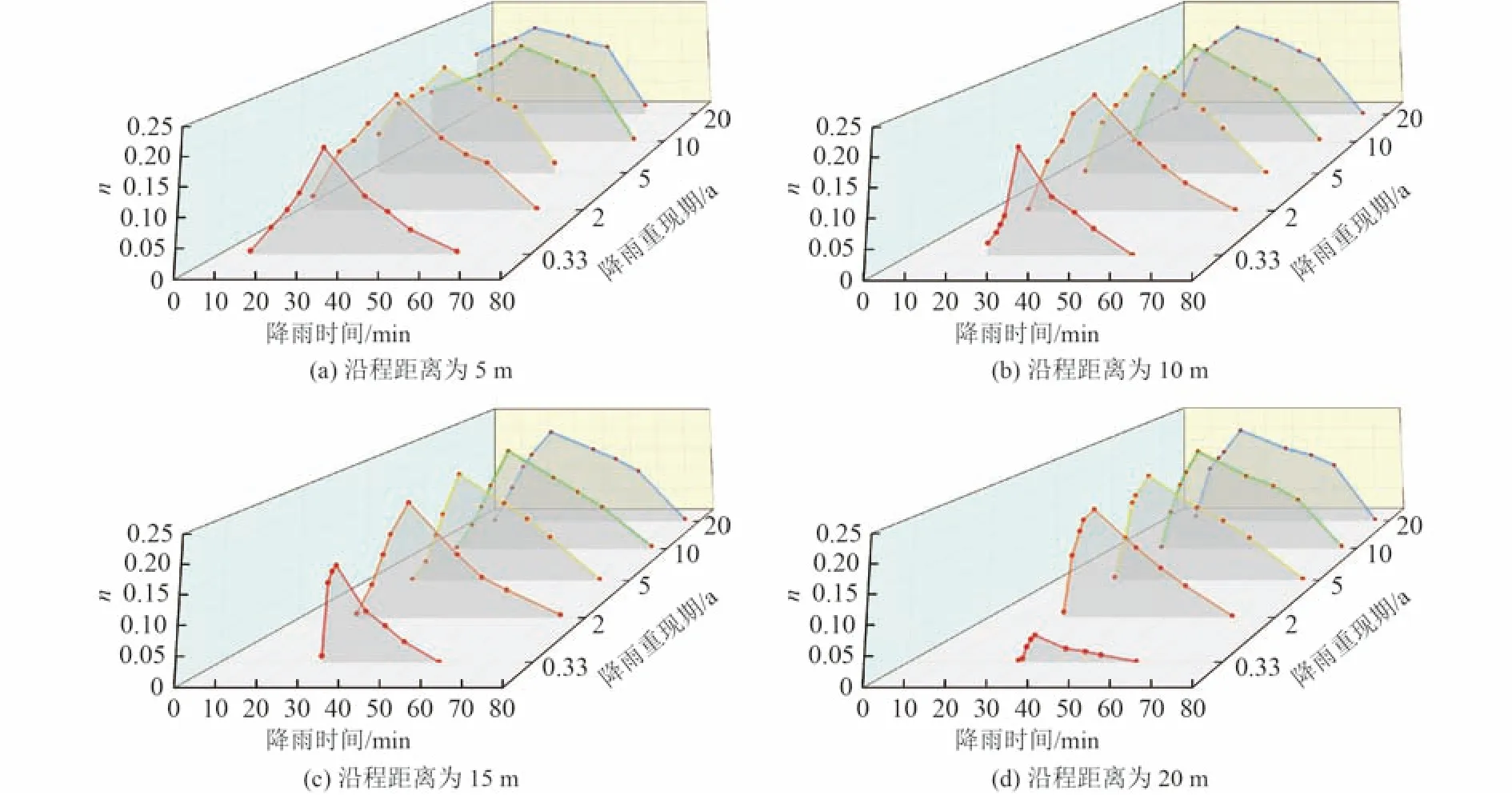
图8 植草沟不同沿程距离n 变化特征Fig.8 Variation characteristics of Manning roughness coefficient at different monitoring locations along grass swale
通过进一步对比植草沟沿程不同距离处n的变化曲线,可以得出不同沿程距离:当进水的降雨重现期为2、5、10、20 a 时,峰值流量时刻n的变化范围为0.21~0.22;但当降雨重现期为0.33 a 时,不同沿程距离的峰值流量时刻n明显降低。在植草沟沿程距离为5、10、15、20 m 时,峰值流量时刻n分别为0.18、0.18、0.16、0.04,可见n受进水流量变化的影响较大。分析原因是在不同变流量进水条件下,植草沟内水深均小于植被高度(23 cm),当沿程流量增加时,水深也随着增加,进而会导致湿周增大,植被的浸没深度增加,而n与阻水面积相关。
2.3 植被高度对曼宁粗糙系数的影响
已有研究表明,植草沟内植被参数对于n以及水力特性具有显著影响,如Zhang 等[27]在理论分析的基础上,建立了关于自然河流中n与植被面积覆盖率的公式,结果表明,n在不同植被面积覆盖率的河道上呈现出与水深相同的变化趋势,均随着沿程距离的增加而下降。Kirby 等[28]研究了在水深显著小于植被高度时,蓝草、蜈蚣草和结缕草的沿程流量变化曲线,得出n与流速、水力半径乘积的关系。本研究为了进一步分析植被高度对n的影响,研究了植被高度分别为1、15、23 cm 时n的变化特征,峰值流量处n变化过程如图9 所示。
由图9 可知,当植草沟植被高度不同时,随着沿程距离的增加,n均随着进水流量的增加而增加,其最大值为0.22。当植被高度为15、23 cm,在不同降雨重现期以及不同沿程距离处,峰值流量时刻的n相同;而植被高度为1 cm 时,峰值流量时刻n为0.19~0.22,均低于植被高度15、23 cm 时的值,但相差较小。说明植被高度对于n的影响较小。分析其原因是在试验过程中植草沟内水深较浅,且均远小于15、23 cm 的植被高度,进而导致n无显著差异。
采用式(11)进一步计算不同植被高度时,不同沿程距离峰值流量时刻的n沿程衰减率,可以发现,不同植被高度条件下,峰值流量时刻的n沿程衰减率均随与进水口距离的增加呈现上升趋势,与恒定流量进水条件下n衰减率的变化趋势相同。另外,随着Q进增加,不同植被高度条件下,n沿程衰减率均呈现降低的变化趋势,当降雨重现期为2、5、10 a,植被高度为1 cm 时,峰值流量时刻n在出水口处的沿程衰减率分别为13.64%、9.10%、4.55%;而植被高度为15、23 cm,降雨重现期为2、5 a 时,峰值流量时刻n在出水口处的沿程衰减率分别为9.09%、4.55%,降雨重现期为10 a 时峰值流量时刻n均为0.22;相同降雨重现期进水条件下,当植草沟植被高度为1 cm 时,其出水口处对应的n沿程衰减率高于植被高度为15、23 cm 时的值。因此,植被高度对n的沿程衰减率有一定影响。
3 结论
(1)在恒定流量进水条件下,植草沟沿程流量随着与进水口距离增加而降低,随着进水流量的增大,沿程流量实测值与理论值的误差逐渐减小,曼宁粗糙系数是导致实测值与理论值存在误差的主要因素,其随植草沟进水流量的增加而增加。
(2)在变进水流量条件下,植草沟的曼宁粗糙系数与沿程流量的变化密切相关,随沿程流量的增加而增加,其原因是曼宁粗糙系数与阻水面积相关。当沿程流量减小时,植被的浸没深度随之减小,导致阻水面积减小,进而使植草沟的曼宁粗糙系数减小。不同进水流量条件下,峰值流量时刻曼宁粗糙系数最大为0.18~0.22,接近《海绵城市建设技术指南——低影响开发雨水系统构建》中的下限值(0.20~0.30),因此在实际的工程应用中,应根据设计降雨重现期合理选择曼宁粗糙系数。
(3)试验条件下植被高度对于曼宁粗糙系数的影响较小,其变化趋势与沿程流量变化趋势一致,其中最大值为0.22。另外,随着降雨重现期的增大,不同植被高度的曼宁粗糙系数在出水口处的沿程衰减率均呈降低的趋势,在相同降雨重现期进水条件下,植被高度较小时其出水口处的曼宁粗糙系数沿程衰减率较高。
