海流海浪耦合作用对台风浪影响的数值研究

李近元，王 宇，曹淑刚，刘金全，李红有，方念乔

（1. 中国地质大学（北京） 海洋学院，北京 100083；2. 龙源（北京）风电工程设计咨询有限公司，北京 100034；3. 国家海洋局 北海海洋工程勘察研究院，山东 青岛 266061）

我国海上风电发展迅速，截至2021 年4 月，海上风电总装机容量达到1 042 万kW，跃居世界第一。随着近海可开发资源的减少，深远海漂浮式海上风电成为新的热点。海浪无时无刻不在影响着近海的水动力环境[1]，是海洋工程必须考虑的动力要素之一。相比于近岸海洋工程，漂浮式海上风电工程设计对波浪参数的准确性要求更高，目前多年一遇波浪参数的计算一般基于工程位置年度波浪极值数据。通常情况下，工程位置处缺少长期观测资料，海浪年极值数据基本依靠数值计算得到，结果准确性依赖于数值模式的准确性。目前，海流和水位变化对波浪的传播具有调制作用已是共识。例如Tolman[2]的研究指出，受近岸的潮汐和风暴潮影响，海浪参数中会出现相应周期的波动信号。我国学者基于数值模式针对不同海域也得到了类似的结果，例如：魏艳等[3]针对台湾海峡的研究发现，潮流可以导致海浪有效波高呈现明显潮周期的振荡；刘娜等[4]的研究指出，对西北太平洋的海浪模拟时，考虑海流的影响对改善海浪的预报效果具有重要意义；冯兴如等[5]也认为采用海浪-海流耦合模式来研究近岸波浪的长期变化特征会更加准确。但是在目前工程应用中，采用浪流耦合模式计算多年一遇波浪重现期参数仍不多见，且在研究方面，也少有针对海上风电场区域（水深10～50 m 区域）。因此，有必要针对海上风电场区研究海流和水位作用对海浪传播过程的影响，从而为波浪参数推算方法提供新的思路。本文以福建南日岛海上漂浮式风电场区为例，研究了不同相对位置台风路径条件下，海流对海浪的影响程度。针对福建南日岛海上风电场区域建立了高分辨率的海浪-海流耦合模式并进行了验证，之后选取历史典型台风过程，探讨了单独海浪模式和浪流耦合模式海浪结果的区别，并进行了深入的对比分析。

1 模式介绍

本文采用第五代ECMWF（European Centre for Medium-Range Weather Forecasts）大气再分析全球气候数据与台风模型融合风场，驱动单独的海浪和海流-海浪耦合模式，并对模拟结果进行了对比分析。所用海浪模式为第三代海浪模式SWAN（Simulating Waves Nearshore），海流-海浪耦合模式为ADCIRC-SWAN（Advanced Circulation Model-Simulating Waves Nearshore）。

1.1 海流模型ADCIRC 介绍

海流模式为ADCIRC （Advanced Circulation Model），由美国北卡罗来纳州大学和诺特丹大学共同开发[6]，是一种非结构网格、有限元水文动力模式，具有计算效率高、计算稳定的特点。目前该模式已经在国内外得到了广泛的应用。ADCIRC 模式既可以采用垂向平均的二维模式运行，也可以采用三维模式，本研究采用其二维模式，在笛卡尔直角坐标系下的连续和运动方程组分别如式（1）和（2）所示：

式中：H =h+ζ，H 为总水位，ζ 为偏离平均海平面的水位，h 为地形水深；U 和V 分别为x 和y 方向的垂向平均速度；f 为科氏参数；g 为重力加速度；Ps为海表面的大气压强； ρ0为 参考密度； η为牛顿平衡潮势；α 为有效地球弹性系数； τsx和 τsy分 别为外强迫的表面应力在x 和y 方向的分量； τbx和τby分别为底应力在x 和y 方向的2 个分量；Mx和My分别为x 和y 方向的垂向平均在侧边界应力梯度；D 为动量耗散项；Bx和By分别为x 和y 方向的垂向平均斜压梯度。该模型空间上采用有限元方法进行求解，时间上采用有限差分方法，其他更进一步详细介绍可参见文献[7]。

1.2 海浪模型SWAN 介绍

SWAN 是由荷兰Delft 技术大学（Delft University of Technology）研制开发的第三代近岸浅水海浪数值计算模式，该模式采用基于能量守恒原理的平衡方程，除了考虑第三代海浪模式共有的特点外，它还充分考虑了模式在浅水模拟的各种需要。本文采用其基于三角形网格的版本[8-9]。其波作用量平衡方程可表示为：

式中：左边第1 项为波作用量（能量密度与相对频率之比）随时间的变化率；第2 和第3 项为Ν 在空间上的传播；第4 项为由于流场和水深所引起的Ν 在σ 空间的变化；第5 项为水深及流场所引起的波浪折射；S 为以谱密度表示的源汇项，包括风能输入、波与波之间非线性相互作用和由于底摩擦、白浪、破碎等引起的能量损耗。

1.3 风场模型

本文选择的风场为ERA5 风场与圆对称台风模型计算风场的融合风场，其中ERA5 是第五代ECMWF 大气再分析全球气候数据。ERA5 数据提供每小时的大气、陆地和海洋气候变量的估计值，地球数据精确到了30 km 网格，包括了137 层的大气数据，空间分辨率为0.25°，时间分辨率为1 h。在台风模型的选择中，本文选用Jelesnianski 圆对称台风模型[10]。模型需要的信息主要有不同时刻台风中心经纬度、中心最大风速和中心气压等。这些数据均来自中国台风网（http://typhoon.weather.com.cn/） 。

为更好刻画台风风场，本文将ERA5 风场作为背景风场，并与圆对称台风模型生成的风场进行融合。风场融合公式如下[11]：

式中： Vm为 台风模型得到的风场； VQ为 背景风场； Ve为重构后的风场；e 为权重系数，其值为：

式中： c=r/(10×R)；r 为计算点距离台风中心的距离；R 为最大风速半径。

1.4 海流-海浪耦合机制

本文对不同台风过程期间海浪的模拟分别采用单独的海浪模式SWAN 和海流-海浪耦合模式ADCIRC-SWAN，采用耦合模式模拟时，ADCIRC 将模拟的水位和流场提供给SWAN 模式，作为海浪模式的背景场；SWAN 模式提供给ADCIRC 的辐射应力将作为外力驱动加入到风应力中。该机制的进一步介绍参见文献[12]。

2 模式设置

本文的海浪模式以及海流-海浪耦合模式采用同一套网格和相同的风场驱动，海流模式开边界采用8 个天文潮驱动，具体设置如下。

1）ADCIRC 模式参数

初始流速和水位为0，固边界的法向水深平均流速为0，开边界条件采用M2、K1、O1、N2、S2、P1和Q1共8 个分潮的调和常数预报的水位作为驱动，开边界数据来自NAO99 潮汐模型[13]。采用耦合模式时，ADCIRC 模式与SWAN 模式交换数据时间间隔为30 min。

2）SWAN 模式参数

初始频率为0.04 Hz, 频率增加因子为1.1，频率数为41，波浪谱方向的分辨率为10°, 模式计算的时间步长为30 min。

3）模拟区域与分辨率

计算网格采用三角网格，计算区域位于（112°～135°E，15°～32°N）范围内，模式的分辨率从外海的30′逐渐过渡到研究海域的150 m，一共68 859 个节点、132 868 个三角形单元。模式网格在研究海域采用海图水深和实测水深，外海采用美国国家地球物理资料中心（National Geophysical Data Center, NGDC）的ETOPO2 数据，其水平分辨率为2′×2′。SWAN 计算网格与ADCIRC 网格一致，研究海域网格如图1 所示。

图1 研究海域计算网格及代表性分析点位P1、P2 位置分布Fig. 1 Calculation grid of the engineering area and distribution of representative analysis points P1 and P2

3 模式验证

为了对耦合模式的海浪模拟结果进行验证，本文搜集了1307 号和1319 号台风过程中的一些海浪观测数据并且与模拟结果进行了对比。这2 个台风均抵近或通过研究海域，1307 号台风通过研究海域时最大风速约38 m/s，等级为台风级别；1319 号台风抵近研究海域时最大风速约45 m/s，等级为强台风级别。台风路径以及用来验证的海洋观测站点分布如图2 所示，验证结果如图3 所示。可以看出，在站位S1、S3、S4 和S5 处，受水位、海流和海浪耦合作用的影响，有效波高的模拟结果出现了和实测资料一致的因潮汐调制而导致的波动信号，其准确度得到明显的提高，这是站位离岸较近、水深较浅、受水位和流速调制明显所致。而站位S2 和S6 由于离岸较远，因此在2 次台风过程中，有效波高受潮汐信号调制不明显。目前的验证结果表明，本文所建立的数值模型基本准确，可用来进一步分析水位、海流和海浪耦合作用对海浪有效波高的影响。且不同位置处，水位、海流和海浪的耦合作用对海浪具有显著不同的影响，有必要进行进一步的研究。

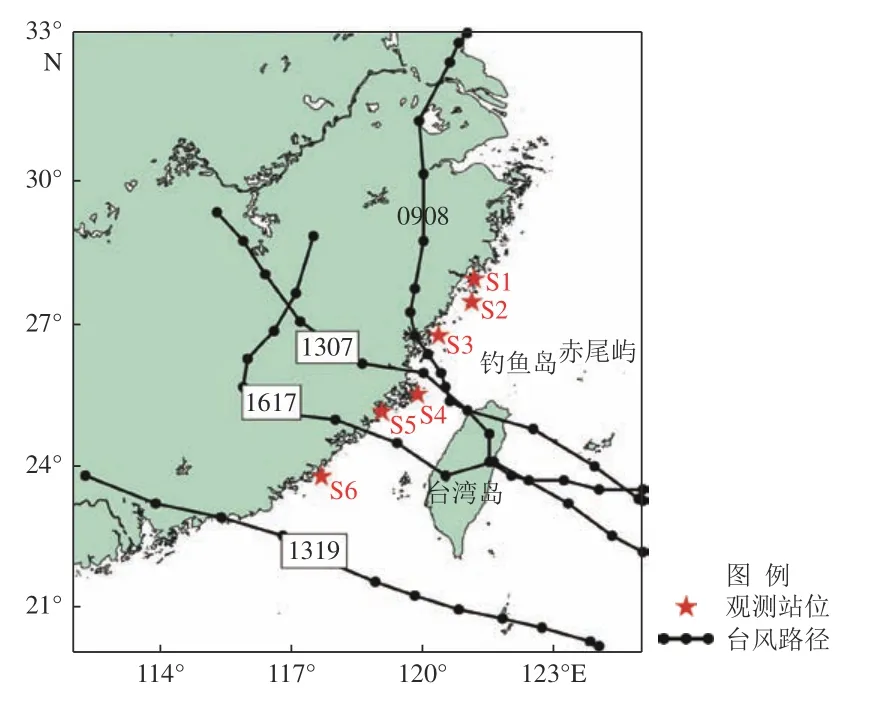
图2 模式验证和结果分析所选取的台风路径及海浪观测站位分布Fig. 2 Distribution of the typhoon paths and wave observation stations used for model validation

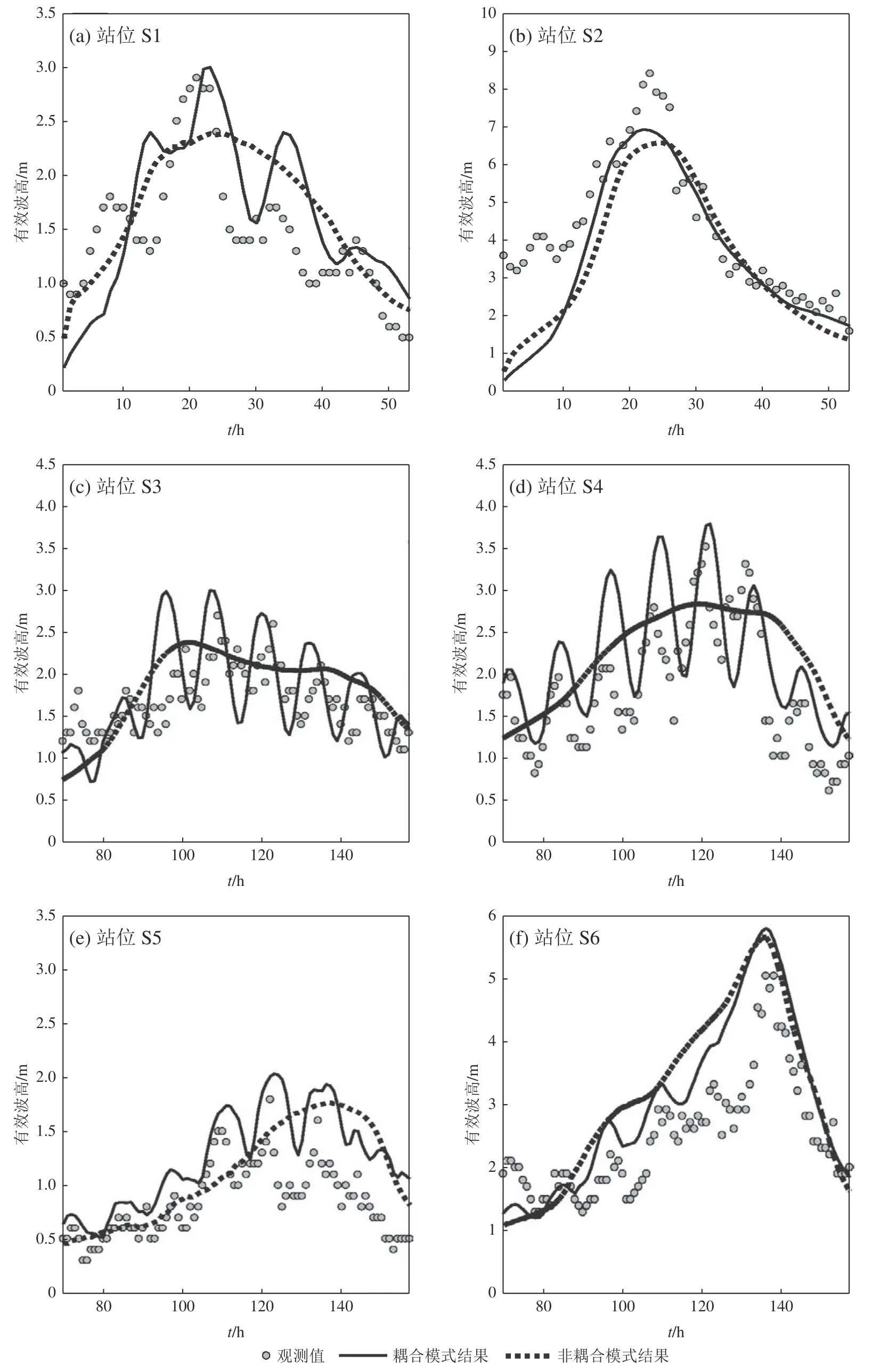
图3 1319 号台风期间海浪有效波高模拟结果和实测结果在站位S1～S6 处的对比Fig. 3 Simulated and observed significant wave heights at stations S1 to S6 during typhoon 1319

4 结果分析

除了用于模式验证的1307 号和1319 号台风过程，本文还分别利用单独的海浪模式以及浪流耦合模式模拟了0908 号和1617 号台风期间的海浪、海流和水位，从而刻画不同相对位置处台风过程中海浪传播特征的差别。0908 号台风抵近研究海域时最大风速约33 m/s，为台风级别；1617 号台风通过研究海域时最大风速约35 m/s，为台风级别。这4 个台风的路径如图2 所示。为揭示浪流耦合作用对海浪的影响，首先针对福建南日岛附近海域分析4 个典型台风过程期间浪流耦合作用对最大有效波高影响的空间分布，之后选取位于研究海域外海侧的2 个代表位置，进一步分析了浪流耦合作用对波高影响的原因以及对海浪传播方向和谱峰周期的影响。

4.1 浪流耦合作用对波高影响的空间分布

利用耦合模式模拟得到的最大有效波高（Hsmax_couple）减去单独海浪模式模拟获得的最大有效波高（Hsmax_wave）代表台风过程中耦合作用对最大有效波高的影响，从而分析耦合作用对海浪的影响。4 次台风过程中Hsmax_couple—Hsmax_wave 的值在研究海域的空间分布如图4 所示。

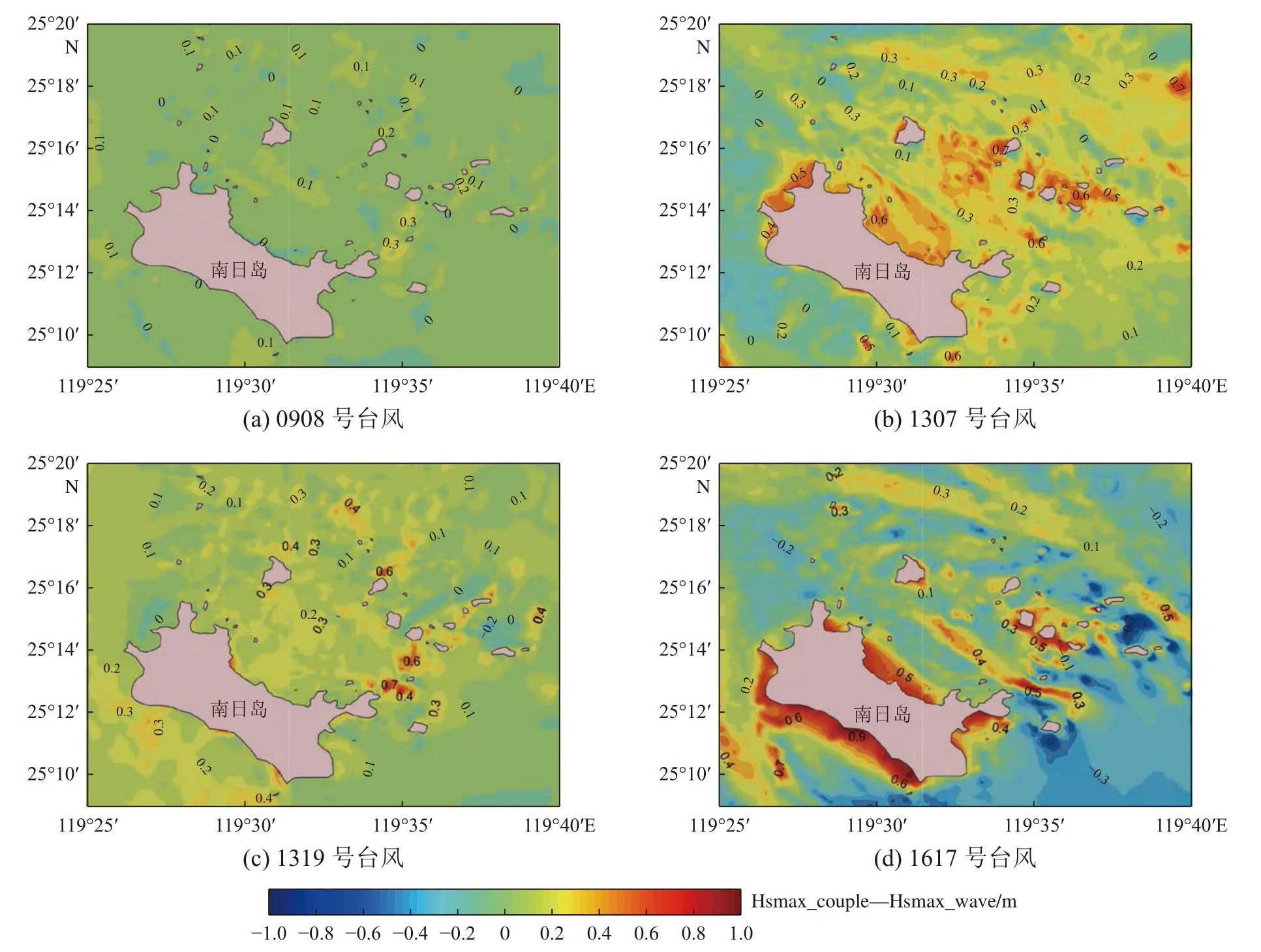
图4 台风过程中耦合作用对最大有效波高的影响Fig. 4 Influence of coupling on the maximum significant wave heights during typhoon

Hsmax_couple—Hsmax_wave 计算结果显示，不同台风过程Hsmax_couple—Hsmax_wave 值的分布有明显不同。0908 号台风过程中，浪流耦合作用对研究海域最大有效波高有普遍的提高作用，考虑耦合作用后，南日岛附近多个区域最大有效波高提高了0.1～0.3 m（图4a）；1307 号台风过程中，浪流耦合作用对最大有效波高的提高作用更加明显，部分区域最大提高了0.7 m 以上（图4b）；1319号台风过程中，在南日岛东南近岸海域浪流耦合作用使得最大有效波高提高0.8 m 以上，同时部分区域浪流耦合作用对最大有效波高也表现出较小的削弱作用（图4c）；1617 号台风过程中，浪流耦合作用对最大有效波高影响的空间差异更加明显，部分岛屿附近出现了0.9 m 以上的削弱，而在南日岛近岸以及部分小岛屿附近则出现了高达1 m 的提高（图4d）。

本节分析显示，对于不同路径和强度的台风过程，浪流耦合作用对最大有效波高影响的空间分布有很大不同，但不管是提高还是降低，都在岛屿或者浅水区域更加明显，这与本文模式验证部分所得结论基本一致。

4.2 浪流耦合作用对波高影响的单点分析

为了探讨浪流耦合作用对波高影响的原因，针对1319 号台风过程中，研究海域P1 和P2 两个代表位置处（图1）海流沿波向的分量、耦合作用对波高影响以及水位的变化过程开展了进一步分析，结果如图5 所示。之所以选择这两个点，是因为P1 处不同实验波高结果差别明显，P2 点则代表更偏近岸的位置。其中，海流沿波向的分量Uw=Ucos（θ），U 为海流速度，θ 为海流方向与波浪传播方向之间的夹角，Uw的正和负分别代表海流沿波向的分量与波向相同和相反；Hsmax_couple—Hsmax_wave 代表耦合作用对波高的影响。

图5 1319 号台风过程中P1 和P2 位置处海流沿波向分量、耦合作用对波高影响（有效波高差值）及水位过程曲线Fig. 5 The wave direction component of the current, the influence of coupling on wave height (difference of significant wave height) and the stage hydrograph curves of water level at stations P1 and P2 during typhoon 1319

由图5 可知，在1319 号台风过程中，P1 和P2 点位处耦合模式和单独海浪模式输出有效波高的差别均有潮周期的变化，说明耦合作用对波高的调制效果明显。一般在理想情况下认为，当海流和海浪同向时，波高会减小，海流和海浪反向时有利于波高增加[14]。本文的数值分析结果也基本符合这一理论，在1319 号台风过程中，P1 位置处沿波向的流速分量大部分时间是负值（图5a），海流与波浪传播反向明显，从而导致耦合作用对波高的影响大部分时间表现为升高（图5b），同时值得一提的是，图5a 中海流沿波向的分量达到负的极值时刻，基本对应图5b 中有效波高变化为正的极值时刻。而在P2 位置处，海流沿波向的分量大部分时间是正值（图5d），海流与波浪传播同向明显，从而导致耦合作用对波高的影响大部分时间表现为削弱（图5e），此外，图5d 中海流沿波向的分量达到正的极值时刻，基本对应图5e 中有效波高变化为负的极值时刻。这2 个点位处有效波高的差别变化（图5b 和图5d）与水位位相变化没有很好的对应关系，这也许因为用来分析的2 个点位水深较深，均在25 m 以上，潮位变化对总水深影响不显著。

4.3 浪流耦合作用对波向和谱峰周期的影响分析

对1319 号台风过程中，浪流耦合作用对P1 和P2 位置处波向和谱峰周期的影响也进行了分析。该台风过程中，单独海浪模式和耦合模式输出的波向和谱峰周期的结果见图6。可以看出，相对于单独的海浪模式，耦合模式得到的波向和周期可以看出明显的潮周期信号，说明波向和谱峰周期受浪流耦合作用调制也比较显著。以P1 点位为例，在1319 号台风过程中，相对单独海浪模式结果，浪流耦合作用可使波向变化达到20°，谱峰周期变化可达2 s 以上。说明浪流耦合作用无论对于波向还是谱峰周期，其调制作用都是不可忽视的。

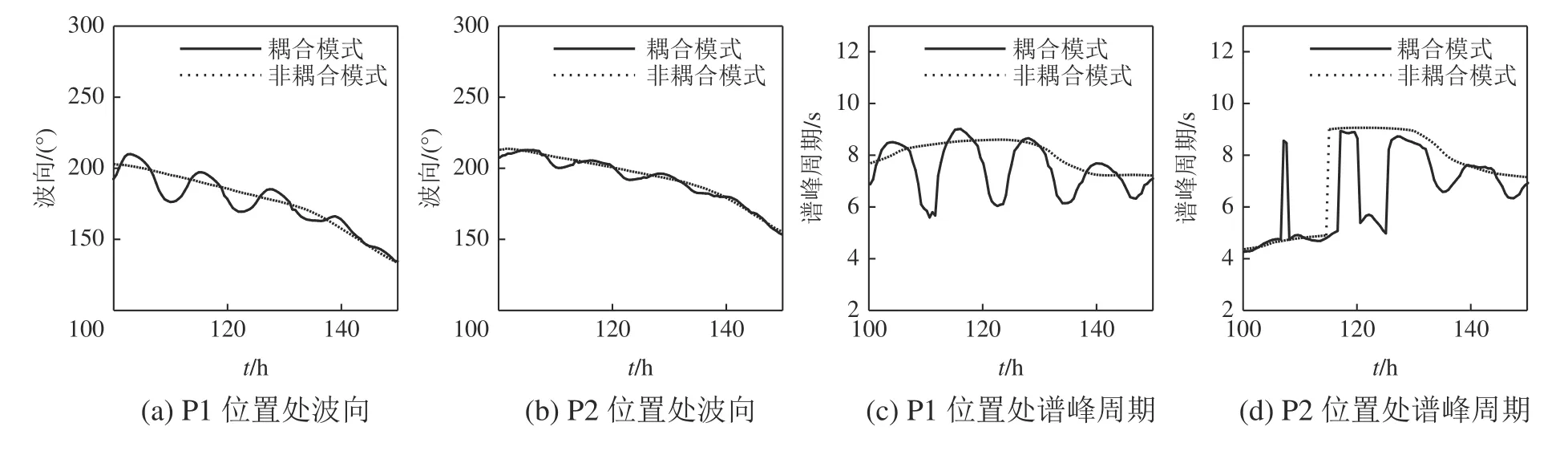
图6 1319 号台风过程中P1 和P2 位置处波向和谱峰周期变化过程曲线Fig. 6 During typhoon 1319 Wave direction and spectral peak periodic variation curve at P1 and P2

5 结 论

本文基于海流和海浪耦合模式，以福建南日岛海上风电场海域为研究区域，研究了台风条件下海流和水位变化对波浪的调制作用，得到如下主要结论。

1）针对研究海域建立了高分辨率的海浪-海流耦合数值模型，对台风过程中有效波高模拟结果的验证显示，采用耦合模式能得到更加准确的波浪结果，再现近岸波高变化中的潮周期信号。

2）不同台风过程中，浪流耦合作用对最大有效波高影响的空间分布差异明显，本文的4 次台风过程中，耦合作用对研究海域最大有效波高的影响可达—1.0～1.0 m。

3）对单点的模拟结果分析发现，流向和浪向同向时对浪高有削弱作用，反向时对浪高有增强作用，这与已有结论相符。此外，浪流耦合作用对波向和谱峰周期也有明显的影响。

4）对于波向和谱峰周期，浪流耦合作用对于波向和谱峰周期的调制也是显著的。P1 位置在1319 号台风过程中，波向变化可达20°，谱峰周期变化可达2 s。

综上，本文结果显示浪流耦合作用对台风条件下波浪影响显著，结论与已有研究成果基本相符[1,7]。本文的研究意义在于针对具体研究海域研究了浪流耦合作用对台风浪影响的具体过程，进一步明确了采用海浪-海流耦合模式在重现海浪极值中的重要性，加深了在浅水海域浪流相互作用对台风浪波高和周期影响的机理认识，同时对海上工程设计也具有重要参考价值。