挑流鼻坎体型数值模拟优化研究

赵兴龙,韩 雷,王正君,吕春玮,叶昆河,田振华

(1.黑龙江大学 水利电力学院,哈尔滨 150080;2.黑龙江省水利科学研究院,哈尔滨 150080)

0 引 言

水库溢洪道的泄洪消能一直是水工建筑物的研究重点,相较于传统物理模型试验的研究方法,通过数值模拟对溢洪道进行水力特性的研究得到了更普遍的应用［1］。何志亚等［2］〗针对沙河水库溢洪道挑流鼻坎采用FLUENT软件对拟定的挑流鼻坎进行数值模拟,并进行了推荐体型的物理模型试验,得出了能满足挑流水舌落点远离下游崩塌体的挑流鼻坎体型。郭红民等［3］通过建立溢流堰挑流消能的三维数值模型,并对模型试验结果进行验证,同时对多种优化消能方案进行数值模拟计算,得出了在原体型的基础上适当增大挑流反弧半径可以改善泄流消能作用。马强［4］通过数值模拟和模型试验进行验证,建立了两种不同的尾坎并进行数值模拟,得出了下游河道差动式最大流速比连续式最大流速小的结论。张桂花等［5］提出了一种舌瓣鼻坎挑流新体型,并对其进行了物理模型试验,研究表明该体型增加了水舌挑距,避免了水舌集中冲刷河床。

本文采用数值模拟与物理模型试验相结合的方式,利用物理模型试验得到的结果对数值模拟进行验证。在验证满足误差范围内的基础上,采用数值模拟的方法对该水库溢洪道进行挑流鼻坎优化研究,为挑流鼻坎的体型设计及优化提供参考。

1 工程概况

某水库由拦河坝(包括大坝和二坝)、溢洪道和引水发电系统等组成。本工程为一等工程,拦河坝及溢洪道为一级建筑物,500年一遇洪水设计,可能最大洪水校核;引水建筑物及电站厂房为二级建筑物,50年一遇洪水设计,500年一遇洪水校核。溢洪道位于右岸低分水岭处,为开敞式岸坡溢洪道,由引水渠、溢流堰体、泻槽、挑流鼻坎及出水渠等5部分组成,总长959.50m。设7个溢流孔,堰顶高程205.60m,每孔净宽16m。设16×13.4m弧形工作门,采用固定卷扬式弧门启闭机操作,弧门前设一道平板检修闸门,7孔设1套。设计洪水位220.58m时下泄流量为12 210 m3/s,校核洪水位225.41m时下泄流量为18 570 m3/s。矩形断面泄槽由130m宽渐变至90m。

2 物理模型试验

为验证数值模拟和物理模型试验的准确性,设计原连续式挑流鼻坎的模型试验。模型按照重力相似准则设计,为正态模型,由上游库区、溢流堰(引水渠、溢流堰体、泄槽、挑流鼻坎及出水渠)、下游河道组成。

2.1 比尺设计

模型整体布置按照1∶100的几何比尺在试验场按原地形制作,主要比尺关系见表1。

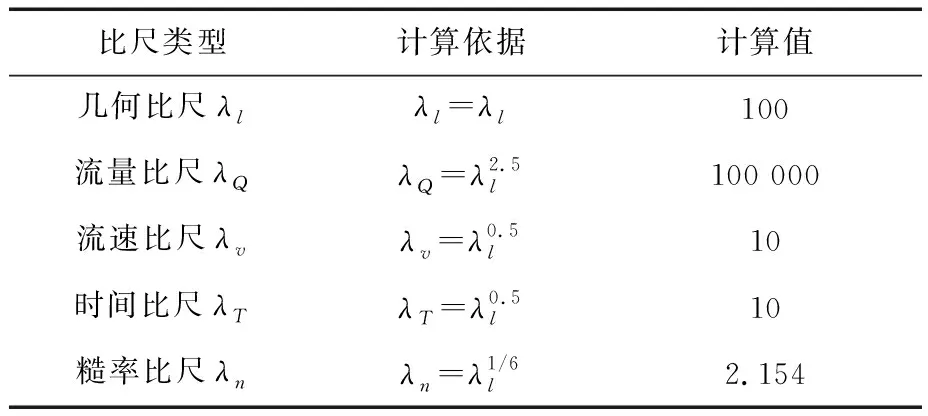
表1 模型主要比尺

2.2 模型制作

非溢流坝段采用砖混结构,溢流坝模型采用有机玻璃制作,库区及下游河道地形采用定床凹形模板制作。原型溢流坝采用常态混凝土,其糙率n=0.014～0.017。根据糙率比尺,计算模型材料的糙率比尺为0.0065～0.0079,有机玻璃的糙率n=0.008,基本可以满足糙率相似要求,选择有机玻璃制作溢流坝模型。加工精度控制在±0.2mm以内,安装的垂向精度控制在±0.3mm以内,平面精度控制在±0.5mm以内。模型整体布置见图1。

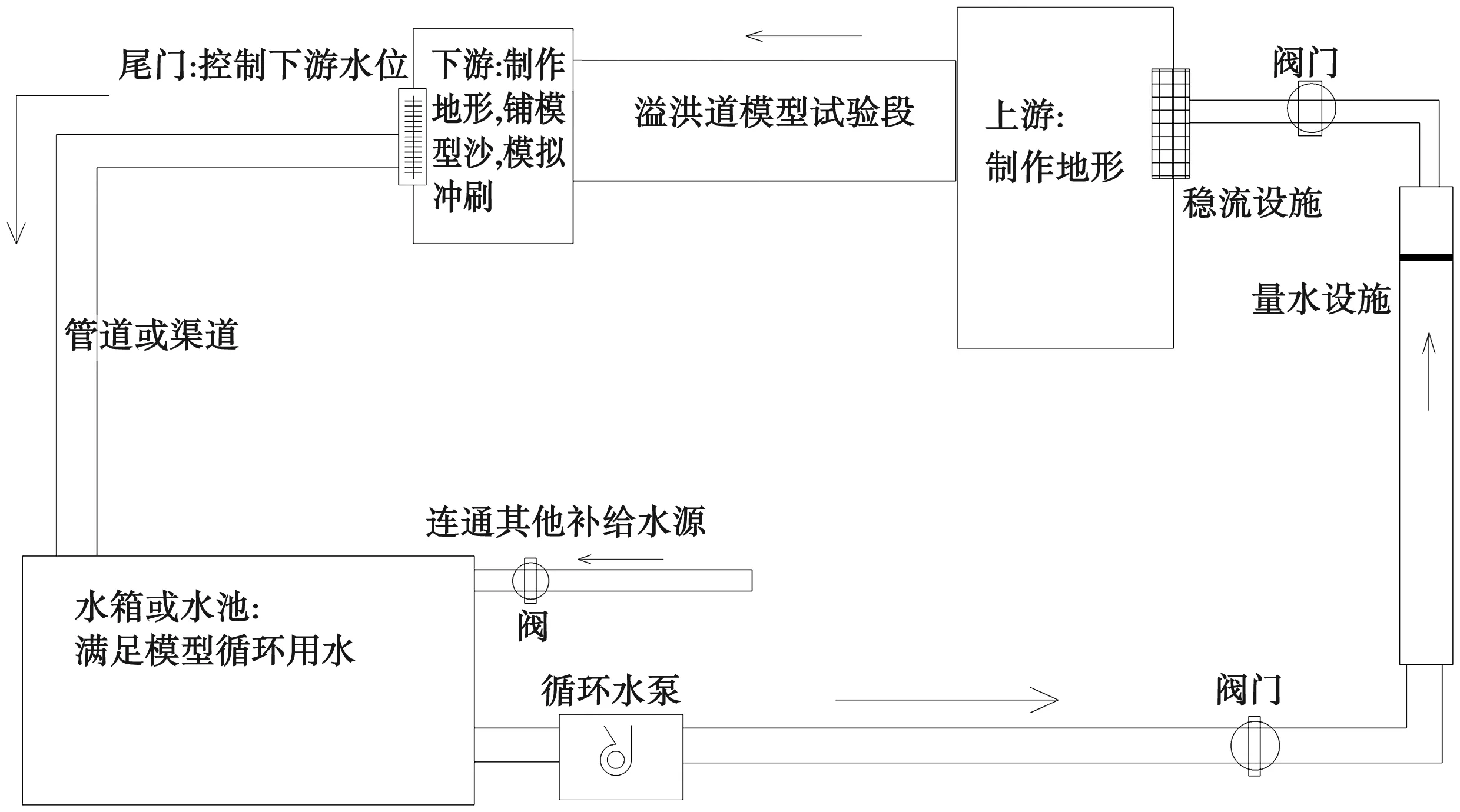
图1 溢洪道物理模型试验流程示意图

3 数值模拟计算及验证

采用有限体积法进行离散,采用VOF自由追踪液面、RNGk-ε湍流模型和PISO算法对原连续式挑流鼻坎进行数值模拟,并与物理模型试验进行验证。

3.1 控制方程

数学模型采用RNGk-ε湍流模型,可以更好地处理高应变率及流线弯曲程度较大的流动,具有更高的精度和可信度［6］。其控制方程为:

连续方程:

(1)

动量方程(Navier-Stokes方程):

(2)

k-ε紊流方程:

(3)

(4)

3.2 网格划分

数学模型设顺溢洪道方向为X方向,沿溢洪道从右岸到左岸方向为Y方向,垂直方向为Z方向。采用结构化网格进行划分,引水渠、溢流堰体、泄槽及出水渠网格间距为2m,挑流鼻坎段网格间距为0.5m,模型共有网格总数为2 262 005个。

3.3 边界条件设置

数值模拟计算中,引水渠入流断面设置为进口边界,采用压力进口,通过给定水位和流速的方法来保持恒定的流量;出水渠出口断面设置为出口边界,同样采用压力进口,通过给定水位来保持下游河道的水位恒定。各工况设置边界条件见表2。

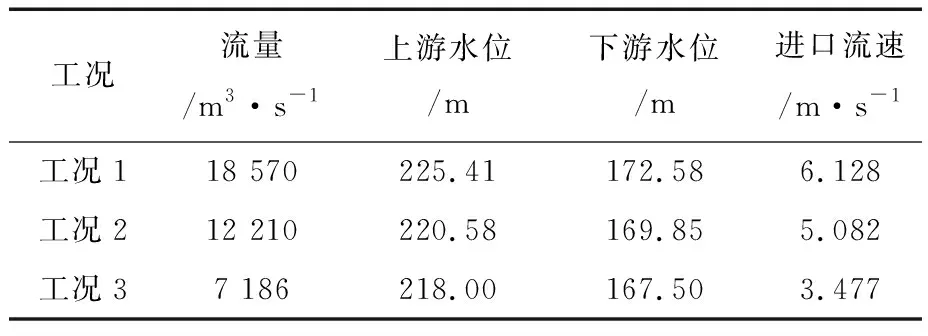
表2 各工况设置边界条件

3.4 模型验证

本文针对原连续式挑流鼻坎体型(鼻坎挑角30°,挑流鼻坎反弧半径30m,挑流鼻坎尾部高程179.6m),在泄洪流量为18 570、12 210、7 186m3/s,相应上游水位分别为225.41m(工况1)、220.58m(工况2)、218.00m(工况3)3种运行工况条件下,进行数值模拟与物理模型试验结果比较。

3.4.1 流量对比分析

表3为3种工况下数值模拟和物理模型试验的流量。由表3可以看出,数值模拟计算值的进口流量和模型试验的实测值所采用的进口流量数据基本一致,两者的相对误差在允许范围内。

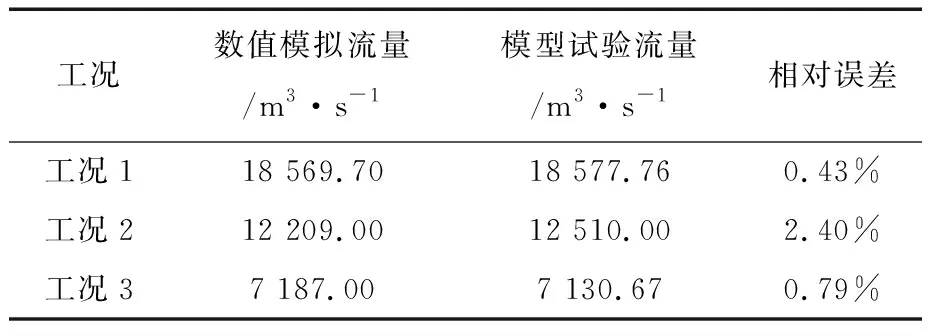
表3 数值模拟与物理模型试验流量对比表

3.4.2 水面线对比分析

图2为3种工况下数值模拟和物理模型试验的水面线对比图。由图2可以看出,数值模拟计算值和模型试验实测值有略微差异,主要表现为模型试验实测值略高于数值模拟计算值,但是两者基本相同,误差在允许范围之内。同时可以看出,随着流量的增大,两者水面线的拟合程度越来越好,这可能与大流量状态下流体流动相对更稳定有关。

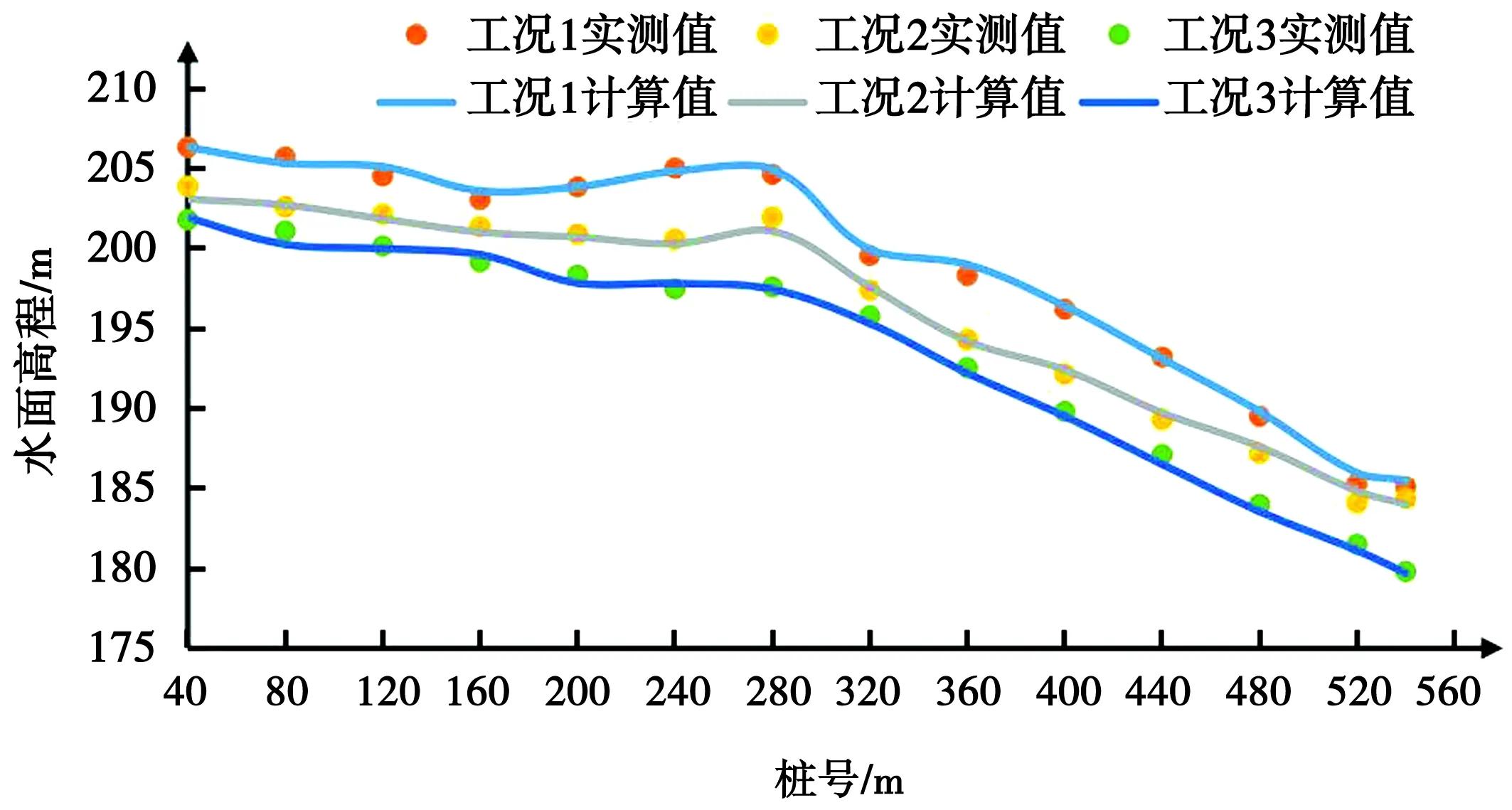
图2 各工况下水面线实测值与计算值对比分析

3.4.3 流速对比分析

由图3可以看出,工况1计算值和实测值误差最大值发生在桩号0+280m处,误差值3.72%;工况2计算值和实测值误差最大值发生在桩号0+540m处,误差值3.41%;工况3计算值和实测值误差最大值发生在桩号0+120m处,误差值3.74%。泄漕段与挑流鼻坎段的流速吻合良好,整体误差满足精度需求。

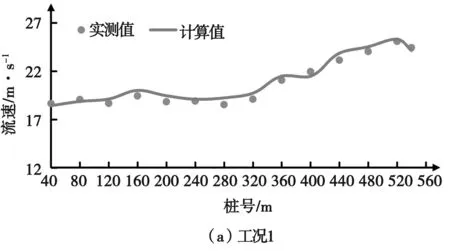
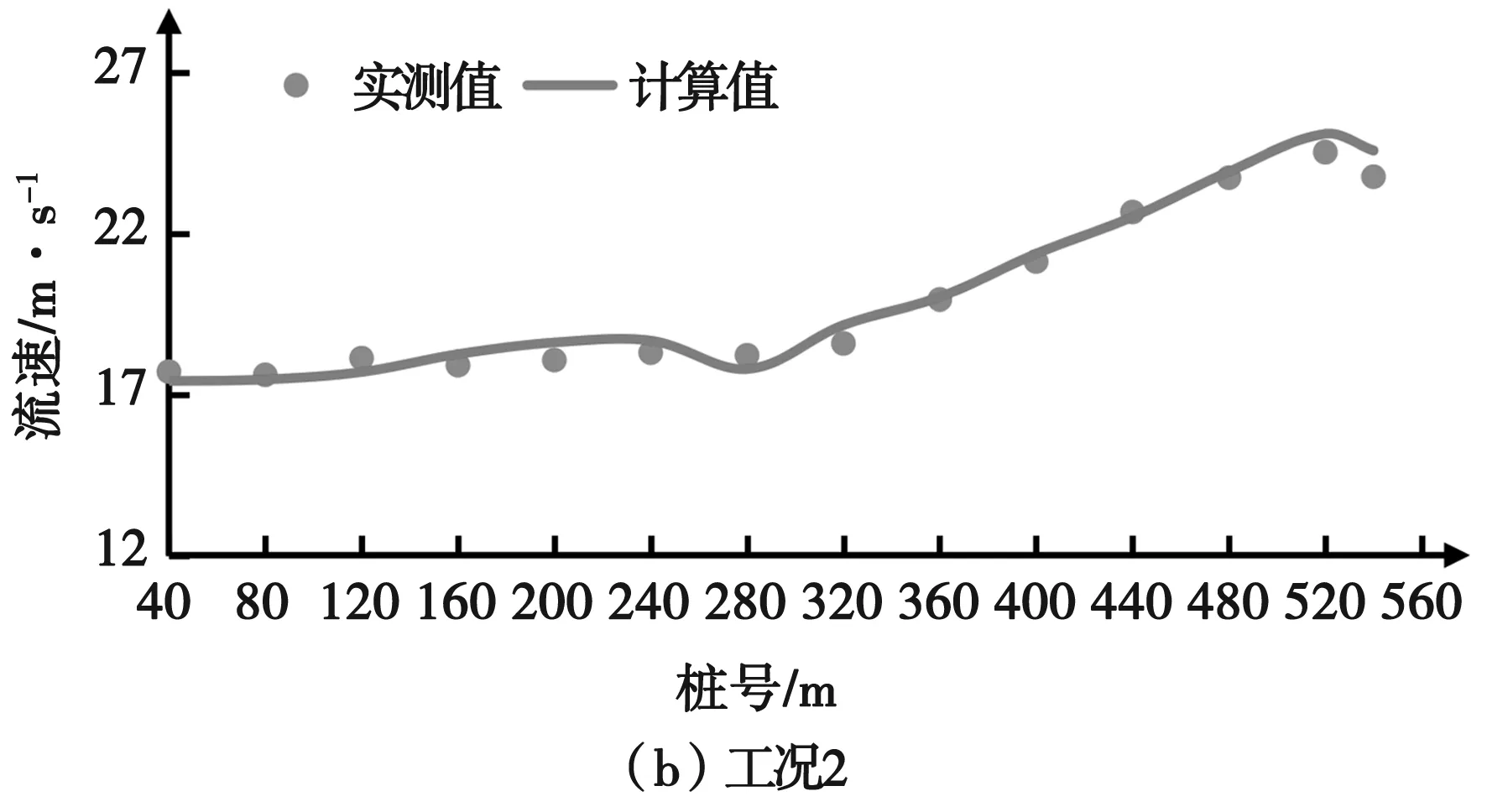
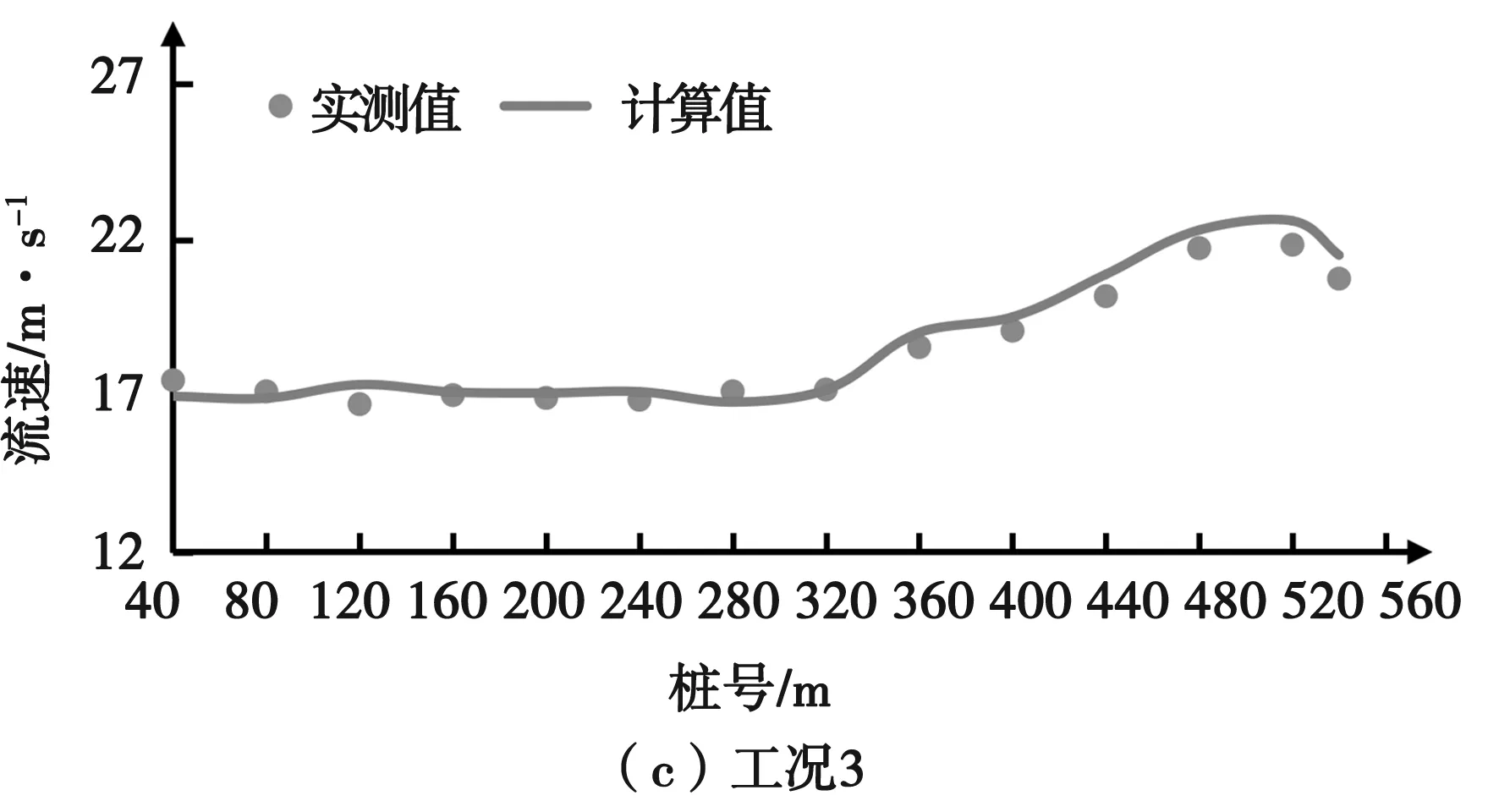
图3 典型断面数值模拟与模型试验流速对比图

3.4.4 挑射水舌形态对比分析

图4对比了数值模拟与物理模型试验挑射水流的水舌形态。数值模拟计算流态良好,与物理模型试验流态吻合度极高。

图4 溢洪道挑流鼻坎段数值模拟与物理模型试验水流流态对比

3.4.5 挑射水舌挑距对比分析

表4为3种工况下挑流鼻坎挑射水舌挑距的数值模拟计算值和物理模型试验实测值结果比较。由表4可以看出,两者的结果基本吻合,但某些地方存在着一定的误差,。误差值最大的是工况2的内缘挑距为6.5%,这可能是物理模型试验由于水流的脉动现象导致水舌的落水点具有随机性,同时模型试验自身缩尺效应也会对结果产生一定的影响。

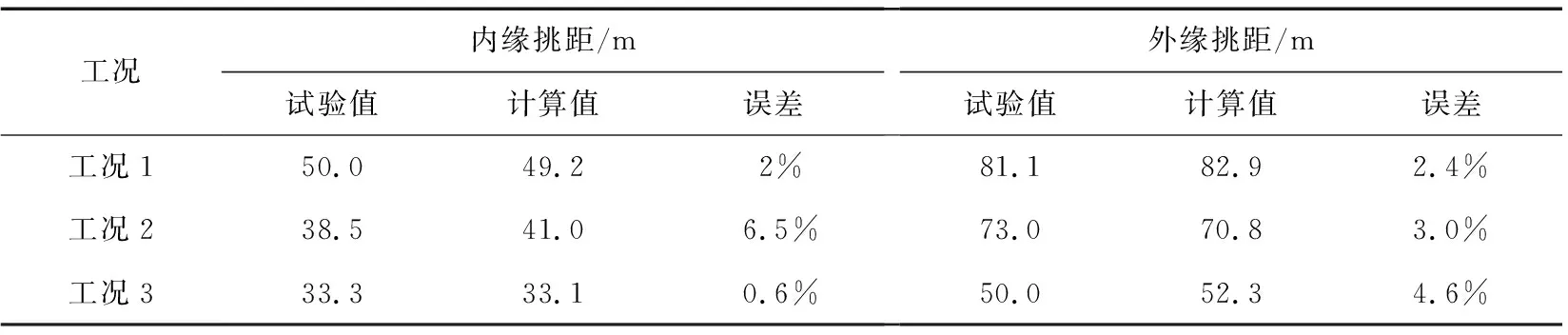
表4 数值模拟与模型试验挑射水舌挑距对比表

4 消能工体型优化

该水库溢洪道原连续式挑流鼻坎体型存在水流落点过于集中的问题,为了更好地分散水流,减轻对下游河道的集中冲刷,对消能工体型各参数进行优化。参考类似工程以往的经验,采用双圆弧差动式挑流鼻坎,以增加挑流水舌在空气中的掺气程度,解决挑射水流落点过于集中的问题。

4.1 双圆弧差动式挑流鼻坎设计

根据该水库溢洪道的特点,对其进行体型优化。在优化体型设计时,主要考虑以下要求:在原连续式挑流鼻坎体型的基础上,仅做少量改变,以求便于施工,同时可以达到较好的消能效果。经研究,最终采用双圆弧差动式挑流鼻坎,高坎和低坎高度差为4m,以泄洪流量12 210m3/s(P=0.2%)为主要研究对象进行数值模拟,比较优化体型与原体型的挑流消能效果。双圆弧挑流鼻坎三维效果见图5。

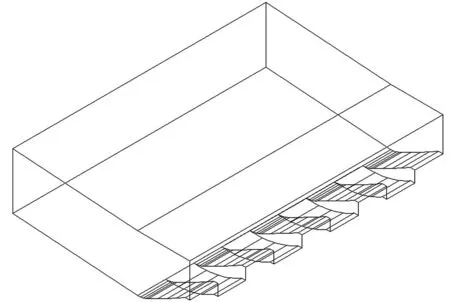
图5 双圆弧挑流鼻坎三维效果示意图

4.2 水舌形态分析

图6为溢洪道工况2数值模拟原体型与优化体型挑射水舌形态对比图。由图6可以看出,优化体型相较于原体型水舌前后的水流落点更分散,入射角更小,挑流水舌形态更好。同时可以看出,优化体型的挑射水流与下游河道中的水流碰撞更充分,更有利于消能。

图6 溢洪道工况2数值模拟原体型与优化体型挑射水舌形态对比

4.3 水舌挑距分析

表5为原体型与优化体型在12 210m3/s的泄洪流量下的内缘挑距和外缘挑距。由表5可以看出,优化体型的內缘挑距和外缘挑距都小于原体型,但优化体型挑射水流入下游河道处的长度要大于原体型,有利于分散水流,提高了挑射水流在空中的耗能率,减小了对下游河道的冲刷,且优化体型的水舌落水点对坝基不产生危害。

表5 原体型与优化体型水舌挑距对比表

4.4 消能率分析

水库溢洪道挑流消能率计算方式各有不同。本文的溢洪道挑流消能率可表示为［4,7］：

η=(E1-E2)/E1×100%

(5)

其中:E1=Z+V21/(2g);E2=V22/(2g)

式中:E1、E2分别为该水库溢洪道上下游断面的水流总能量;V1、V2分别为上下游断面平均流速,以下游断面平均水深为基准高程;Z为上游库区断面与下游断面的高程差。

采用流量为12 210m3/s时的消能率进行对比,原连续式挑流鼻坎的消能率为73.5%;双圆弧差动式挑流鼻坎的消能率为79.7%。可以看出,优化体型的消能率大于原体型的消能率,双圆弧差动式挑流鼻坎的消能效果优化明显,可提高该水库溢洪道的消能效果,从而减小挑射水流对下游河道的影响。

5 结 语

1)通过FLUENT计算流体软件,对某水库溢洪道挑流鼻坎进行数学模型分析,得到的结果与物理模型试验基本一致。数学模型计算成果提供了比物理模型试验更为全面的数据,为物理模型试验做了很好的补充。

2)本文对某水库溢洪道挑流鼻坎进行优化,对比分析了双圆弧差动式挑流鼻坎与原连续式挑流鼻坎在水舌形态、水舌挑距、消能率方面的计算结果。数据表明,采用双圆弧差动式挑流鼻坎可以分散水舌,避免水流落点过于集中,消能率提高了6.2%,有效降低了对下游河床的冲刷。