基于Box-Cox 变换与随机系数回归模型的非线性退化设备剩余寿命预测方法

杨保奎，张建勋，李慧琴，司小胜

火箭军工程大学 智剑实验室，西安 710025

随着科学技术的不断进步，各类设备呈现出集成化、智能化、多元化、复杂化的发展态势（例如，航空发动机、导弹、核电站等）。与此同时，这些设备的造价也愈发高昂。受内在机制演化、外部环境改变等因素影响，设备往往会不可避免地发生退化，导致其使用性能降低及健康状态劣化。如果单个设备模块或者关键部件出现退化，则有可能造成整个设备发生故障，甚至引起失效并造成不可估量的人员财产损失。实践表明，寿命预测与健康管理（Prognostics and Health Man‐agement，PHM）技术对于降低设备的故障率和提高设备的可靠性具有重要的理论研究价值与实际工程意义［1-4］。

剩余寿命（Remaining Useful Life，RUL）预测技术作为PHM 领域的核心，旨在通过设备的退化监测数据准确预测设备的剩余使用寿命，是降低设备计划外失效风险、及时对退化设备进行维护、减少设备维护时间和费用的关键技术［5-6］。作为一类典型的数据驱动的设备剩余寿命预测方法，基于随机系数回归模型的剩余寿命预测研究开展较早。20 世纪90 年代初，Lu 和Meeker［7］首次提出了一般随机系数回归模型用于设备退化数据的建模及寿命预测。在该模型基础上，出现了很多进一步的扩展研究，例如：Elwany 和Gebraeel［8-9］对随机系数回归模型参数估计的方法进行了改进并应用于剩余寿命预测中；Wang［10］对随机系数回归模型的建模思想和应用中存在的问题进行了总结；Fang 等［11］提出一种自适应预测缺失数据的回归模型，利用自适应回归函数对信号特征及其相应的失效时间进行建模。目前，随机系数回归模型作为一类能较好体现退化过程随机性的线性模型，国内外学者不断研究其在剩余寿命预测领域的应用与创新。Yan等［12］利用一种迭代更新回归模型刻画轴承健康指标的退化趋势，并结合基于蒙塞尔变换的关键点检测自适应方法，提高轴承剩余寿命的预测性能；万昌豪等［13］克服工程实际中剩余寿命预测先验信息不足的问题，基于非线性随机系数模型进行退化建模；Tang 等［14］针对一类软故障退化系统，提出一种具有时间效应的随机系数自回归模型描述退化过程，并利用Bayesian 理论周期性更新随机系数，同时优化了动态条件下的维护策略；Ahsan 和Lemma［15］利用自回归模型预测了燃气涡轮发动机的剩余寿命。

然而，需要注意的是，随机系数回归模型较为依赖历史退化监测数据的质量。在现有的基于随机系数回归模型的剩余寿命预测研究中，特别是对于一些非线性设备的退化数据，主要通过时间尺度变换［16］、对数变换［17］等变换技术进行线性化处理，将非线性退化数据变换为近似线性退化数据，然后建立线性退化模型用于剩余寿命预测。例如，Zhou 等［18］构建一种考虑退化速率与退化波动率依赖关系的广义非线性Wiener 退化模型，该模型具有时变的均值方差比，并推导出近似剩余寿命的封闭解，进一步确定估计参数初始值和时间尺度函数的方法；Yu 等［19］利用年龄依赖状态空间模型构建了一种考虑三源不确定性的非线性漂移Wiener 模型，并用涡扇发动机退化数据和合金疲劳裂纹数据进行实验验证；Zhang等［20］提出了一种非线性漂移分数布朗运动的锂电池剩余寿命预测方法，该模型将非线性函数的所有参数定义为锂离子电池退化模型的特定隐藏状态变量；Xi 等［21］用与时间相关的非线性函数代替漂移项，用以描述系统退化过程复杂的非线性特征；Shahkar 和Khorasani［22］提出了一种非线性多变量Bayesian 模型，以解决单次测量无法得到足够系统状态信息的情况。但是，时间尺度变换、对数变换等技术的适用目标较为单一、变换函数的形式较为有限，限制了其在实际中的应用。同时，对于非线性退化数据，直接采用非线性随机模型进行建模的方法较大地依赖于非线性函数形式的选择，而对于工程实际中的非线性退化数据选择何种非线性函数本身是一个难题。

针对以上问题，本文提出基于Box-Cox 变换（Box-Cox Transformation，BCT）与随机系数回归模型的非线性退化设备剩余寿命预测方法。相比于时间尺度变换、对数变换等变换技术，BCT 的优点在于可以使变换后的回归模型满足线性、独立性、齐方差性、正态性，同时BCT 的函数形式更具有一般性，可以将多种常见的变化包含在特例中。在采用BCT 和随机系数回归模型的基础上，运用Bayesian 理论与蒙特卡罗-期望最大化（Monte Carlo Expected Maximization，MCEM）算法对退化模型的参数进行在线更新。考虑到本文方法中，不仅需要在Bayesian 框架下进行退化模型参数的后验估计，还需对模型其他未知参数进行估计，而常用的期望最大化（Ex‐pectation Maximization，EM）算法需要在其E 步求解完全数据对数似然函数的条件期望，但该条件期望显示表达式的获得较为困难，因此本文采用MCEM 算法［23］来近似计算E 步的条件期望。根据模型参数的在线估计，推导剩余寿命的概率密度函数及点估计值，并通过数值仿真和锂电池实际退化数据验证本文所提方法的有效性。

1 基于BCT 与随机系数回归模型的退化建模

1.1 退化建模

对于非线性退化设备的退化量X(t)，首先采用Box-Cox 变换对退化数据进行线性化处理，然后再采用线性随机系数回归模型对变换后的数据进行建模。Box-Cox 变换是在1964 年由Box和Cox［24-25］提出的一种应用非常广泛的广义幂变换方法，通过计算分析变换参数λ得到最优的BCT，用以改善原始退化数据的线性、独立性、齐方差性以及正态性，其一般形式可表示为

式中：X(t)为原始退化量；λ为变换参数；Z(t，λ)为变换后的退化量；相应逆变换可表示为

针对变换后的退化变量Z(t，λ)，考虑到BCT的非线性数据线性化能力，采用式（3）线性随机系数回归模型对其时变演变过程进行建模

1.2 模型参数估计

1）离线估计

2）参数在线更新

根据式（3）的性质特点和Bayesian 公式，可知：tk时刻模型随机参数φ、θ的后验分布为两变量正态分布，相应的后验分布参数为

1.3 基于MCEM 算法的参数校准

由于随机参数θ、φ无法直接测量，通过式（7）直接计算超参数Θ的极大似然估计值较为困难。现有研究中常用EM 算法解决此类参数估计问题，但对于EM 算法，难以求解其E 步积分的显式表达式，且迭代优化过程较长。为解决这一问题，本文引入MCEM 算法来优化模型超参数估计过程，提高收敛速度，具体实现过程如下。

进一步，结合式（8）、式（10）可得

2 剩余寿命预测

在1.2、1.3 节求出随机参数的后验估计后，接下来是求解设备RUL 的分布。为此，本文假定退化过程Z(t，λ)到达给定的失效阈值时发生故障（失效阈值为w，且w>0），这样，求解剩余寿命的分布就转化为求解退化过程到达失效阈值的时间分布。

将退化过程中tk时刻至失效时刻之间的间隔表示为T，即为设备tk时刻的RUL，那么就有Z(λ)(tk+t)=w，则剩余寿命的条件累积分布函数为

根据剩余寿命的定义其取值为非负的，即T≥0，所以需要对增加这一约束条件，那么剩余寿命的分布函数可以进一步表示为

基于以上结果，可以通过微分求得剩余寿命的条件概率密度函数为

式中：ϕ(·)为标准正态随机变量的概率密度函数。

直接对式（20）求解剩余寿命的点估计较为困难，而上文已经得到Z(λ)(tk+t)=w，将式（17）中t+tk时刻预测的均值代替Z(λ)(tk+t)，即w=，则可以求得tk时刻RUL 的近似点估计为

式中：RULk为本文方法对应RUL 的点估计。

3 数值分析与实例验证

3.1 数值分析

为验证本文模型的有效性，首先通过数值例子进行仿真。基于数值仿真数据，对模型参数进行初始化：μφ0=0.02，=0.2，μθ0=0.05，=0.01，=0.004，λ=0.41，失效阈值给定为2.5，采样间隔为5。为进一步体现本文方法的优越性，引入文献［13］进行对比实验，其模型为

式中：x0为初始状态，且x0=0；Λ(t；θ)为非线性函数，一般传统的非线性函数为exp(θt)−1 或tθ，本文令Λ(t；θ)=exp(θt)−1；

进行数值仿真时，令φ～N(0.02，0.000 2)，θ～N(0.005，1.0×10−6)，σ2=0.000 1，文献［13］参数设置与本文模型保持一致，仿真出的轨迹如图1 所示。可以看出经过BCT 后的退化轨迹明显比原始退化仿真轨迹更趋向于线性轨迹；由于文献［13］采用典型的非线性随机系数模型，拟合更一般的退化数据效果明显不如本文方法。此外，变换后的退化数据共有100 个采样点，超过失效阈值的时刻大概为496。

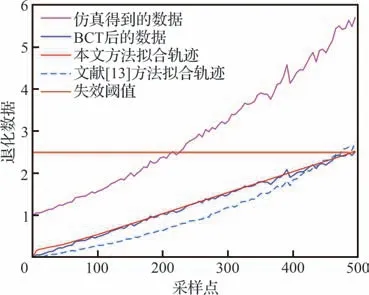
图1 数值仿真与估计的退化轨迹Fig.1 Degradation trajectory of numerical simulation and estimation

通过选取21 组退化仿真数据估计，得到模型参数估计值，具体通过表1 对比真实值可以看出，数据量越大，参数估计越准确。

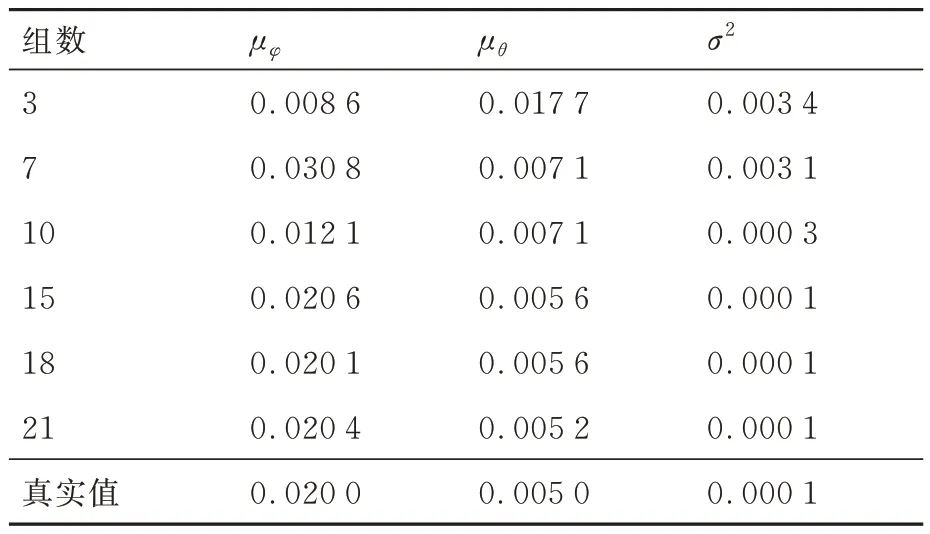
表1 数据累积得到的参数估计结果Table 1 Parameter estimation results obtained by data accumulation

为验证本文采用的BCT 对非线性退化数据线性化的效果，并进一步量化本文模型拟合退化数据的精确度，引入平均预测得分、均方误差、决定系数、相关系数作为性能评价指标［27］。通过分析模型预测的性能，以佐证本文RUL 预测方法的有效性和性能提升程度。

1）平均预测得分（Score）计算公式为

式中：τi=Ti−；Ti为ti时刻非线性退化设备真实的RUL；为ti时刻非线性退化设备RUL 的预测值，本文用退化模型RUL 的点估计表示；n为设备退化总时间。该指标越小，预测结果越准确。

2）均方误差（Mean Squared Error，MSE）计算公式为

式中：Z(ti，λ)为非线性退化数据经过BCT 得到的退化数据；Z′(ti，λ)为经过本文模型得到的退化数据。

MSE 描述了本文模型预测误差平方的均值，该值越小误差越小。

3）决定系数（也称拟合优度，R2）计算公式为

决定系数刻画了模型预测值与真实RUL 的密切程度，该指标取值一般在[0，1]，取值越接近1 表明拟合程度越好。

4）相关系数（也称为关联系数，r）是统计学中重要的评价指标之一，描述2 个变量之间的相互关系和密切程度。本文采用Pearson 相关系数刻画BCT 前的退化数据和变换后退化数据的线性相关程度，其中变换前的相关系数为

变换后的相关系数可表示为

相关系数的绝对值介于0～1，通常情况下，该值越接近于1，表明2 个变量之间的线性相关程度越密切，越接近于0，2 个变量之间的线性相关程度越弱。

5）线性度（又称非线性误差，δ）计算公式为

式中：δ为线性度；xmax、xmin分别为退化数据的最大值和最小值；F为退化数据的拟合函数，可用最小二乘法拟合退化数据的回归方程表示，即

式中：p、q常数。

线性度描述的是在规定变化范围内的实际轨迹偏离拟合特性直线的程度，本文用来描述设备退化数据偏离拟合模型的程度，线性度越接近于0，说明偏离程度越小，线性程度就越好。

给定10、30、60、100 个采样点的仿真退化数据，然后分别对BCT 后数据进行拟合，结果如图2所示。结合图1，发现每增加一定的数据量，拟合程度越高。观察模型整体仿真退化轨迹，如图2（c）所示，可以看出大约在15 个采样点后，模型退化轨迹与变换后的退化轨迹重合；另外，模型仿真数据与BCT 后的数据之间的MSE 为0.001 4，表明本文模型能够较为准确地刻画出变换后的退化数据，体现了本文方法的有效性。

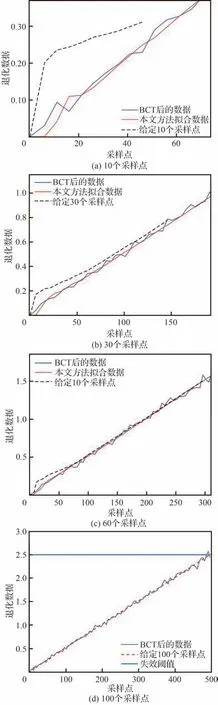
图2 不同采样点下得到的仿真退化轨迹Fig.2 Simulation degradation trajectories obtained at different sampling points

图3 给出了应用本文提出的MCEM 算法更新模型超参数的过程。从图3 可以得到，本文模型的随机参数的均值μφ、μθ分别经过大约21、15 个采样点后与真实的参数值保持相等，收敛速度较快，可见本文采用的MCEM 算法与Bayes‐ian 思想结合的方法估计参数效果十分明显。

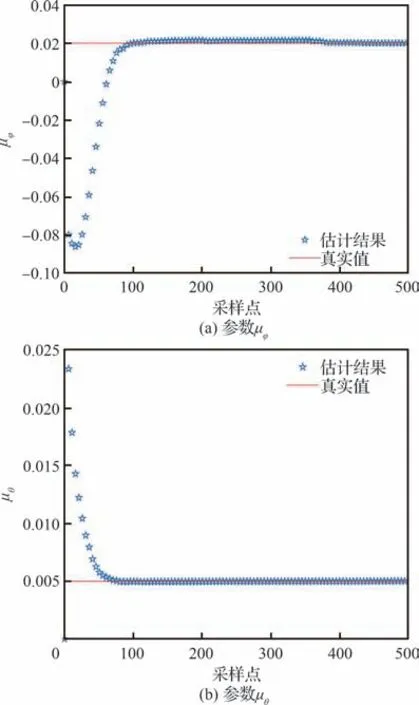
图3 模型参数估计Fig.3 Model parameter estimation

图4为本文模型与文献［13］中的模型在第49个采样点时的RUL 估计及其对应的概率密度函数，从图中可以看出，本文方法预测的结果几乎与真实的RUL 重合，且相较于文献［13］随机性更小，可见本文模型能较为准确地预测出相应时刻的RUL。

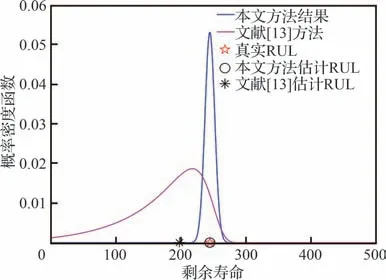
图4 第49 个采样点RUL 的概率密度函数Fig.4 Probability density function of RUL at the 49th sampling point

图5 给出的是通过时间累积得到的RUL 预测结果，图6 为本文模型预测的RUL 及相应的概率密度函数，明显看出在预测初期，模型需要经过约17 个采样点时间后可以得到接近真实的RUL，且后期预测效果精度较高，预测结果较为稳定。

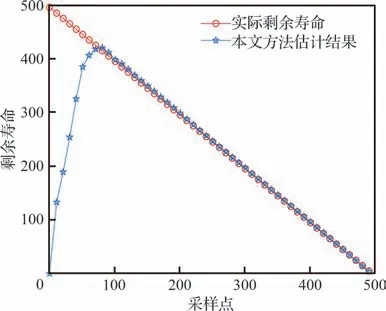
图5 RUL 预测Fig.5 RUL prediction

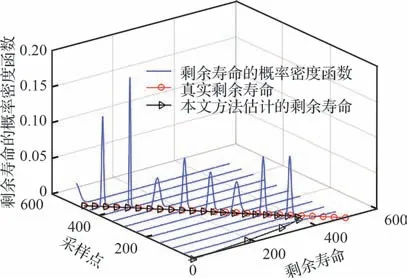
图6 本文方法得到RUL 的概率密度函数Fig.6 Probability density function of RUL obtained by this method

图7 为文献［13］方法预测得到的RUL，预测结果虽能较为迅速地收敛于真实RUL，但预测精度略低于本文模型。图8 为原始数值仿真数据未经过BCT、直接通过本文模型预测得到的RUL，与图6 对比，可以看出虽然预测结果最终仍能收敛于真实RUL，但需要经过约50 个采样点才能较为精准地估计出真实RUL，且随机性较大。可见非线性退化数据经过BCT 后得到近似线性退化数据再进行RUL 预测，效果要优于未经变换的退化数据。

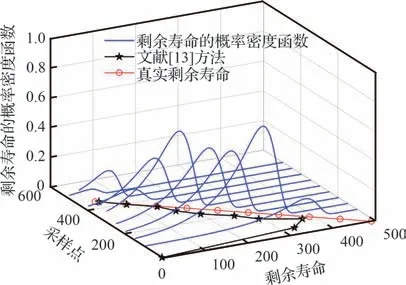
图7 文献［13］方法预测的结果Fig.7 Results predicted by Ref.［13］

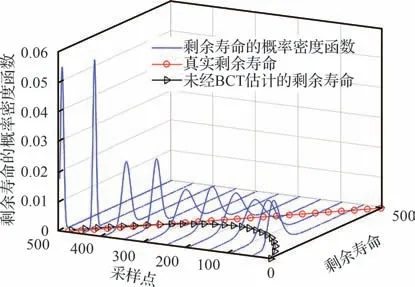
图8 BCT 前数据估计RUL 的概率密度函数Fig.8 Probability density function of RUL estimated by data before BCT

3.2 实例验证

锂电池具有输出电压高、能量密度高、使用寿命长、环境污染低等特点，作为能源储存介质，广泛应用于航空航天、新能源汽车、新能源发电等领域［28-30］。锂电池作为各种设备重要零部件之一，在循环使用时，由于其内部复杂的化学反应、材料的损耗，以及腐蚀、高温环境影响或者使用不当，就可能导致锂电池性能降低和健康状态劣化，直至寿命终止。2019 年4 月19 日，位于美国亚利桑那州的公共服务公用事业公司（APS）电池系统储能电站发生爆炸，直接原因是电芯热失控后爆炸气体累积，和氧气发生化学反应后燃烧；2021 年4 月16 日，北京市丰台区某储能电站由于一座电池间锂电池发生内短路故障，电池模组过热失控引发起火爆炸，事故造成了多人遇难，财产损失高达上千万［31］。因此，为了有效降低成本并维护设备及人员的安全，准确估计出锂电池的剩余寿命，预测健康工作时间就凸显出重要意义。

采用马里兰大学的CS2-38 锂电池的退化数据进行实例研究来验证本文模型的有效性［32-33］。该型号锂电池是在标准的恒定电流/恒定电压协议下，对所有的锂电池进行相同充电过程，在电压达到4.2 V 之前，电流速率保持在0.5 C，之后电压恒定在4.2 V，直至充电电流降到0.05 A 以下。放电过程的截止电压为2.7 V，重复进行充放电实验后，每组数据将会被随机编号。目前，该数据集已被广泛应用于各类锂电池退化与剩余寿命相关实验验证中。

结合2.2 节，对CS2-38 锂电池实际退化数据应用本文提出的BCT 方法，其对应的变换参数的估计值为λ=3.35。计算得到变换前退化数据的相关系数和线性度分别为−0.890 7、22.17%，变换后的分别为−0.970 7、12.96%，并且通过图9 可以看出，锂电池退化数据经过BCT 后线性度明显高于变换前；此外，基于本文方法的拟合轨迹整体上与变换后的退化轨迹重合，但是本文模型由于考虑了退化过程样本数据的差异性，导致整体退化过程的随机性较高于参数φ=0 时的模型，二者MSE 分别为0.045 1、0.005 0，验证了本文所提方法的合理性。

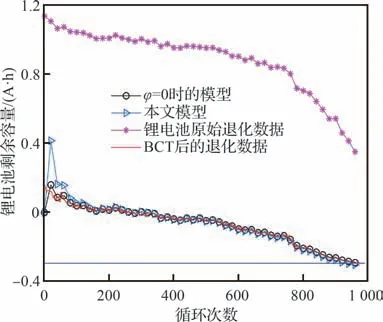
图9 BCT 后及估计的退化轨迹Fig.9 Degradation trajectories after BCT and estimated

图10、图11 分别给出了锂电池退化数据BCT 前、后经过本文模型估计得到的RUL 及其概率密度函数。作为非线性退化数据，虽然通过本文模型也能较为准确地估计出非线性设备的RUL，但随着退化数据的累积，其预测精度和随机性都大于经过BCT 后的预测结果。对比图10、图11，明显看出通过本文方法估计RUL 的随机性逐渐减小，预测精确性也较高，证明了本文基于BCT 方法的优越性。

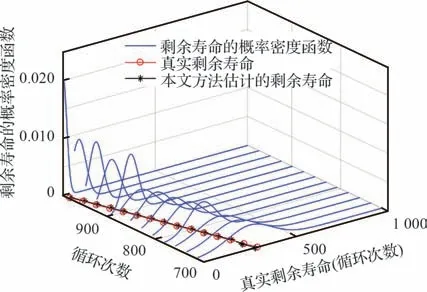
图10 本文模型RUL 的概率密度函数Fig.10 Probability density function for RUL of this model

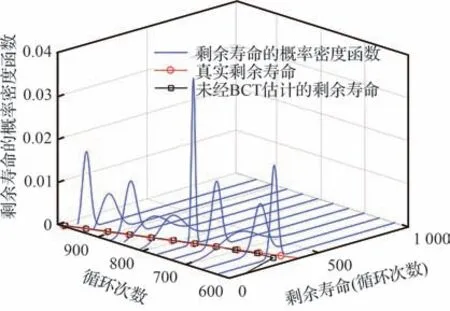
图11 BCT 前数据估计RUL 的概率密度函数Fig.11 Probability density function of RUL estimated by data before BCT

表2 给出了通过仿真退化数据与锂电池退化数据在BCT 前后进行剩余寿命预测时，Score、MSE、R2、r·，t、δ这5 个性能指标对比结果。可以发现，仿真退化数据与锂电池退化退化数据经过BCT 后用于剩余寿命预测，对比采用文献［13］非线性退化模型剩余寿命预测，对应的模型性能指标Score、MSE 均小于变换前的退化数据，而拟合度大于变换前的退化数据；此外，相关系数较BCT 前的退化数据分别有10.05%、8.98%的提升，线性度较变换前的退化数据分别有70.77%、41.54%的提升。综合以上对比结果表明，本文提出的方法在非线性退化设备剩余寿命预测中具有较好的适用性，与已有方法相比在预测性能上拥有一定的优势。

表2 本文模型预测性能对比Table 2 Comparison of model prediction performance

4 结论

针对非线性服役设备剩余寿命预测问题，提出了基于BCT 与随机系数回归模型的非线性设备剩余寿命预测方法，采用BCT 对退化数据进行线性化处理，在此基础上通过随机系数回归模型构建退化模型，运用Bayesian 理论与MCEM 算法在线更新模型参数，推导出了剩余寿命的分布函数以及其点估计值。最后通过数值分析与锂电池非线性退化数据进行验证研究，结果表明：针对非线性退化监测数据，经过BCT 后的退化数据进行建模进而预测剩余寿命，模型拟合度和预测准确性均有显著提升，从而验证了本文方法的有效性和潜在的工程应用价值。