疏松砂岩储层提压注水解堵井周破裂区演化规律分析
2023-07-28牟媚高尚邹剑兰夕堂张丽平王晓超邓九涛
牟媚,高尚,邹剑,兰夕堂,张丽平,王晓超,邓九涛
1.中海石油(中国)有限公司天津分公司(天津 300450)
2.中海油能源发展股份有限公司工程技术分公司(天津 300450)
3.中国石油大学(北京)石油工程学院(北京 102200)
0 引言
在疏松砂岩储层注水生产过程中,由于注入水中悬浮颗粒堵塞[1]、黏土水化膨胀[2]、砂粒运移[3]等原因,可能会堵塞地层孔隙喉道或者形成滤饼,导致储层污染和近井筒堵塞,降低地层渗透率,长期注水生产后油藏吸水能力下降[4]。目前常用压裂、酸化、高压水射流等方法解堵处理[5]。其中,压裂解堵包含常规压裂解堵与提压注水解堵。常规水力压裂解堵技术运用较为普遍,但其由于施工规模小、见水快、解堵有效期较短的特点,具有一定的局限性。短时提压注水通过提高注水压力使之接近或者超过注水破裂压力,在井周附近地层产生微裂缝破坏区,从而改善井周孔渗物性,降低或解除井周污染,穿透污染带,实现解堵增注[6],已在现场取得良好的增注效果[7-8]。在提压注水过程中,若地层岩石破坏较小,则无法达到解堵目的;若地层破裂、裂缝扩展或产生注水裂缝导致注入水窜流又会引发安全问题[9]。因此,出于解堵需求与工程安全考虑,对于提压解堵时井周破裂区的演化分析尤为重要。
疏松砂岩室内岩心实验表明,疏松砂岩岩石强度低,胶结弱,容易发生剪切破坏[10-11]。压裂物理模拟实验表明,不同于常规储层压裂时以拉伸破坏为主,在疏松砂岩储层中,岩石在压裂过程中有可能会形成剪切缝或是复杂的高导流通道[12-13]。成功的短时提压注水需要促使疏松砂岩地层产生破坏,在井周形成合适规模的破坏区,改善井周孔渗物性,同时还需要避免形成过长的拉伸裂缝沟通断层或形成高导流通道引发水窜。针对疏松砂岩复杂破坏形式,使用数值模拟的方法,针对疏松砂岩注水井建立井周变形破裂流固耦合有限元模型,对疏松砂岩储层提压注水解堵进行数值模拟,深入研究疏松砂岩注水井周剪胀扩容机理及其影响规律。
1 疏松砂岩提压注水解堵原理
提压注水解堵或者说微压裂解堵,是指通过提高并维持一段时间注水井注水压力,使近井地带地层孔隙压力升高,储层岩石出现剪切破裂,利用岩石剪切破裂过程中剪胀扩容特性,增加井周孔渗,改善井周堵塞,实现解除堵塞的方法。提压注水解堵不同于其他注水井解堵措施,它仅需提高注水压力——高排量高泵压的注入泵,施工方便,施工器材简单,现场操作性低,具有较好的现场实用性[14]。提压注水解堵措施的解堵作用主要为:注水过程中井周出现剪胀扩容带,形成微压裂区,该区域中,储层孔隙体积变大,微裂缝发育,注水井注入量增加,注入水渗透面积变大,渗透方式变成沿微裂缝高渗通道渗流。
提压注水解堵原理如图1所示。针对提压注水解堵建立地层变形破裂流固耦合模型,对其机理与影响规律进行数值模拟研究。
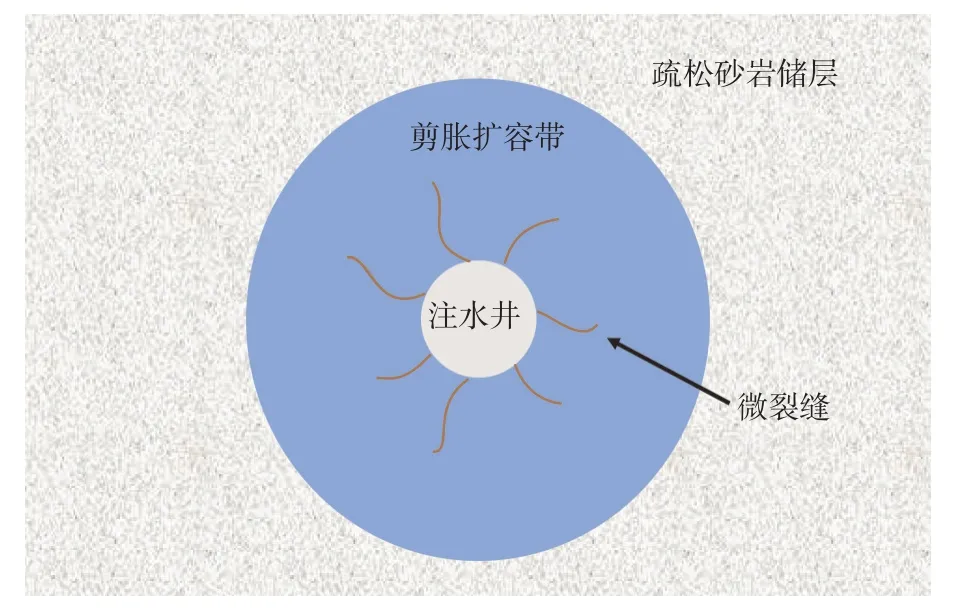
图1 提压注水解堵原理示意图
2 井周变形破坏流固耦合模型
由于疏松砂岩具有高孔渗、低强度的特点,压裂液容易滤失进地层,造成孔隙压力、地应力的变化,导致井周可能出现岩石破坏等后果,继而又影响地层孔渗。所以针对疏松砂岩储层提压注水需考虑到流固耦合效应。
针对疏松砂岩储层内流体流动,使用达西定律进行描述:
式中:qi为储层孔隙内i方向的流体渗流速度,cm2/s;p为孔隙压力,10-1MPa;p,i为孔隙压力p对i求偏导,在i方向的孔压,10-1MPa;μ为孔隙流体动力黏度,MPa·s;k为地层原始渗透率,μm2。
孔隙内流体遵循局部质量平衡方程:
式中:̇为流体含量变化对时间的导数;qi,i为整体流速变化。ζ为多孔弹性介质内孔隙流体含量的变化,由式(3)计算:
式中:p为孔隙压力;εv为体积应变;α为Biot 有效应力系数;M为Biot 模量,其值可以用固相和流体的体积模量来表示。
式中:Ks为固相体积模量,GPa;Kf是流体体积模量,GPa;ϕ为孔隙度,无量纲。
Biot有效应力系数可用式(5)表达:
式中:K为疏松砂岩骨架的体积模量,GPa。
在没有体积力的条件下,平衡方程如下:
式中:σij为总应力;σij,j为在各方向上应力分量对各方向的偏导和。有效应力为:
式中:δij为克罗内克符号。
假设发生的变形为小变形,几何方程有:
式中:εij为应变,无量纲;u为位移,m。
应力与应变之间存在本构关系如下:
式中:G为岩石骨架的剪切模量,GPa;εipj为塑性应变,无量纲。
基于疏松砂岩特性,在室内对疏松砂岩天然岩心进行单三轴力学测试,实验路径及结果见表1。
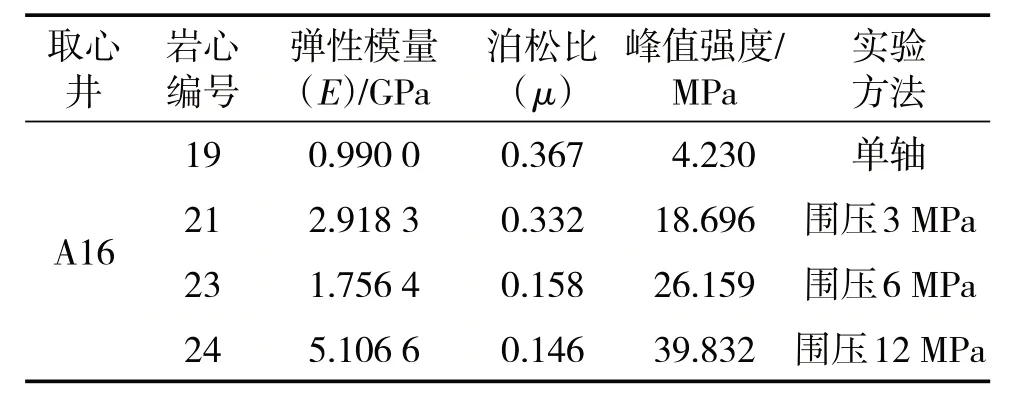
表1 某区块天然岩心三轴测试实验结果
对应力应变曲线结果进行分析,识别出岩心进入屈服或破坏时对应的应力状态点,在平均应力-差应力(p-q)平面上分别拟合岩心的破坏面(红圆数据点)和屈服面(绿方数据点),如图2 所示。采用德鲁克-普拉格/帽盖(Drucker-Prager/Cap)塑性模型来描述疏松砂岩的剪切破坏与塑性压实。

图2 实际实验结果在p-q平面与德鲁克-普拉格/帽盖塑性模型的拟合
当应力状态到达图2 中椭圆帽屈服面时,发生塑性屈服,其表达式为:
式中:帽偏心R与演化系数Pa为控制椭圆帽屈服面形状的材料参数;Pb为静水压缩屈服应力。
由图2拟合可知,Pa=3.2 MPa,Pb=19.1 MPa,当q=0时,屈服应力也为0,代入式(10)可知R=2.00。
当应力状态点到达图2 中剪切破坏线时,发生剪切破坏,其表达式为:
在此天然岩心实例中,fs=y-1.166 4x-4.253 9=0,即内聚力d=4.25 MPa,tanβ=1.166 4,即摩擦角β=49.39°。
同时调研文献可知,疏松砂岩发生剪胀扩容后,相应的破坏区渗透率也会有一定程度的恢复。因此在模型中同步考虑井周地层破坏后的破坏区能够解除污染,在模型中表现为破坏区渗透率的恢复。
3 提压注水解堵机理研究数值模型
基于ABAQUS 有限元模拟软件,建立提压注水井周地层变形破裂流固耦合有限元数值分析模型,基本模型如图3所示。
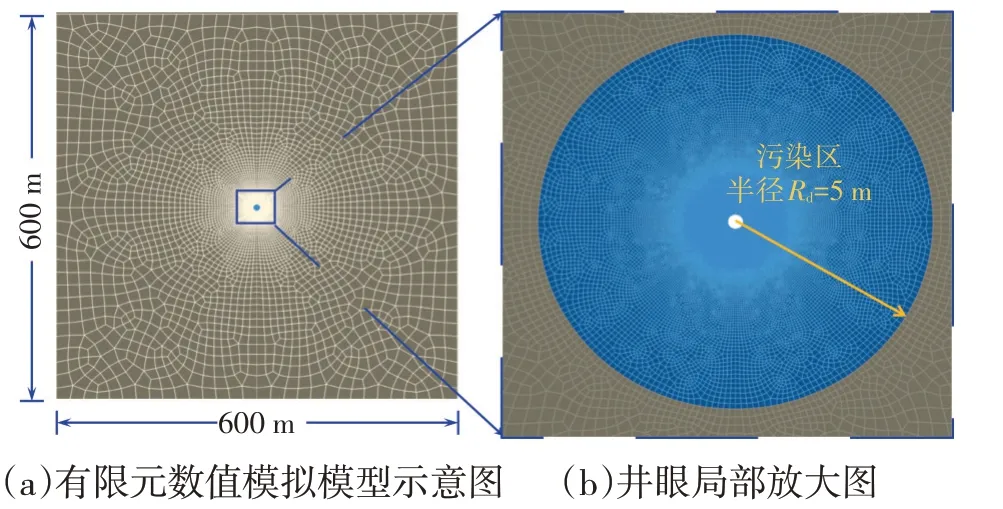
图3 注水井提压注水有限元数值分析模型示意图
参考油田典型疏松砂岩储层现场实测结果,建立提压注水条件下,注水井周地层变形破裂流固耦合有限元数值模拟分析模型。模型如图3所示,参考现场注水井与油井间距300 m,模型边界长600 m,井周预设5 m污染带。通过用户子程序实现对破坏区渗透率变化的模拟。模型基本参数见表2。

表2 模型基本参数
4 注水井周围流体渗流及压力传递规律研究
基于模型模拟计算原始地层渗透率为0.252 μm2、污染带渗透率与地层渗透率比值0.2、注入压力当量密度为2.0 g/cm3、注水时间为3 h 的条件下,注水井井周孔隙压力的变化情况。
如图4 所示,孔隙压力在井口处较大,孔隙压力在水平最大主应力方向波及更大,呈椭圆分布。在注入过程中,注水井周孔隙压力升高,高于岩样强度,井周疏松砂岩出现剪切破坏,井周破裂区扩容导致渗透率增加,进而导致高孔隙压力波及范围增加。

图4 注水结束时井周孔隙压力分布
将最大最小水平主应力方向孔隙压力分布图画出,对比破坏区出现前后与破坏区突破污染带前后孔隙压力分布变化。
如图5 与图6 所示,破裂区剪胀扩容导致渗透率增加,解除了污染带对孔隙压力向外波及的影响,降低了近井地带的孔隙压力梯度。

图5 最小水平地应力方向孔压分布

图6 最大水平地应力方向孔压分布
5 疏松砂岩注水井周破裂区延伸规律研究
5.1 典型工况下井周破裂区分布
针对典型工况,即原始地层渗透率为0.252 μm2(252 mD)、污染带渗透率与地层渗透率比值为0.2、注入压力当量密度为2.0 g/cm3、注水时间为3 h条件下模拟计算注水井周破裂区的延伸情况,计算结果如图7所示。

图7 注水结束时井周破坏区范围
针对模拟结果,若定义破坏区主应力方向的长轴半长为dv,沿最小水平主应力方向的短轴半长为dh,则在典型工况条件下,以2.0 g/cm3当量密度的压力注水3 h,破裂区沿最大主应力方向的长轴长度为dv=16.4 m,此时已突破污染带(红虚线圈所示);破裂区沿最小水平主应力方向的短轴长度dh=4.24 m,还未突破污染带。
5.2 典型井提压注水井周破裂区的影响规律
以上述工况为标准,选用计算参数见表3,分别改变原始地层渗透率、注入时间、注入当量密度,对比数模结果,从而研究各参数对典型井提压注水井周破裂区规模的影响规律。

表3 计算参数
1)注入压力。对比图8中不同注入压力下的井周破裂区规模可以发现,在注入压力当量密度高于破裂压力当量密度(1.7 g/cm3)时,会产生破裂区;而注入压力当量密度越高,在相同时间内,破裂区延伸范围越大。

图8 不同注入压力下的破裂区分布
2)注入时间。对比图9中不同注入时间时的井周破裂区规模可以发现,注入时间增加,破裂区延伸范围变大;注入一定时间后,破裂区的延伸速度减慢,各向趋向均匀。
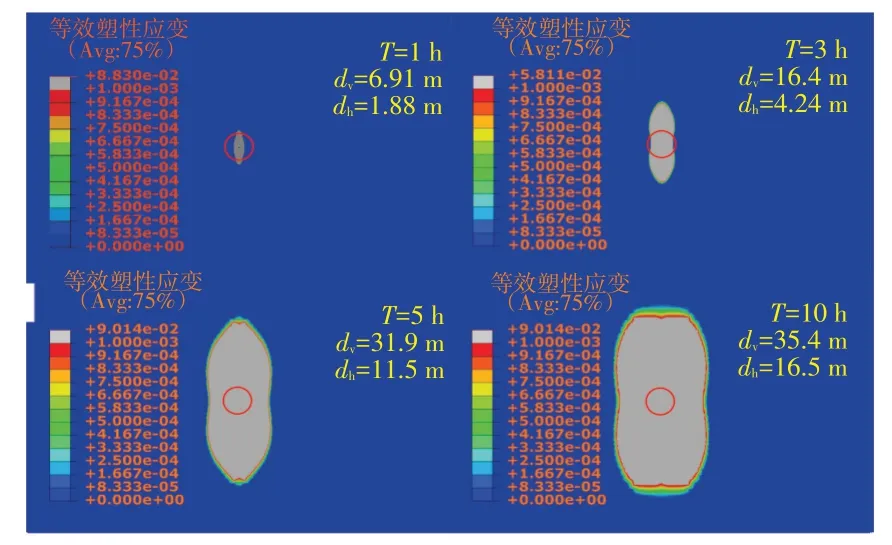
图9 不同注入时间下的破裂区分布
3)地层原始渗透率。对比图10 中不同地层原始渗透率下的井周破裂区规模可以发现,地层原始渗透率越低,破裂区延伸越快,提压注水效果越好。

图10 不同地层原始渗透率下的破裂区分布
结合上述规律,对典型层位提压注水参数进行推荐。结合实验结果,细化不同注入时间下的破坏区规模,如图11所示。

图11 不同注入时间时的破裂区分布
因此,针对渗透率为0.150~0.500 μm2的实际油组,由破裂区参数规律分析可知,注入压力当量密度2.0 g/cm3是合适的,注入2~3 h时,主应力长轴的破裂区能突破污染带且延伸较好,破裂区在长轴方向半长分别为dv=11.2 m,dv=16.4 m,且在3 h时破裂区在短轴方向延接近污染带边缘。当注入1 h 时,在主应力长轴方向突破污染带,破裂区在长轴方向半长dv=6.91 m;当注入5 h,井周完全突破污染带,主应力长轴方向延伸过远。
6 结论
建立了地层变形破裂流固耦合有限元数值分析模型,基于ABAQUS分析注水井井周剪切扩容条件下孔隙压力变化与井周破裂区延伸规律,并针对各因素对井周破裂区影响规律进行研究,结论如下:
1)研究注水井周围流体渗流及压力传递规律发现,在注入过程中,由于近井筒地带孔隙压力升高,导致井周疏松砂岩岩石发生剪切破裂,其破裂区沿最大主应力方向延伸,破裂区扩容会导致渗透率增加,可以解除污染带对孔隙压力向外波及的影响,降低了近井地带的孔隙压力梯度,又进一步促进了高孔隙压力向外波及,实现解堵增注。
2)研究典型井提压注水井周破裂区的影响规律,参数分析结果表明,地层原始渗透率越低,注入压力越高,注入时间越长,近井筒污染程度越小,破裂区延伸范围越大,提压注水效果越好。
