大型中心型换热器内流量分配特性数值分析

2023-07-28肖家禹孙中宁高力陈喜明边浩志

哈尔滨工程大学学报 2023年7期

肖家禹, 孙中宁, 高力, 陈喜明, 边浩志

(1.哈尔滨工程大学核科学与技术学院,黑龙江哈尔滨 150001; 2.哈尔滨工程大学黑龙江省核动力装置性能与设备重点实验室,黑龙江哈尔滨 150001; 3.中国核电工程有限公司, 北京 100840)

为防止发生失水事故(loss of coolant accident,LOCA)或主蒸汽管道破口事故(main steam line break accident,MSLB)时安全壳内超温超压,我国自主研发第三代先进压水堆“华龙一号”配备有非能动安全壳热量导出系统(passive containment heat removal system,PCS)。系统采用集管式换热器作为壳内热阱,通过壳内蒸汽在换热器表面凝结以实现壳内降温降压。换热器作为该系统换热的核心设备,其流量分配情况直接影响换热器换热性能及运行特性,如果结构设计不合理,还可能引起滞流或逆流,甚至引起超温爆管等不良现象[1-2]。因此,实现换热器内流量的均匀分配对于系统的安全、高效运行十分重要。

对于中心型换热器,T型三通区域一直是人们关注的重点。曲新鹤[3]模拟研究发现中心型换热器其T型三通位置形成的涡流将对换热器内流量分配特性产生较大影响。卫飞飞等[4]实验研究了含T型三通联箱,发现三通处形成的涡流会导致该区传热管流量偏低。罗永浩等[5]对T型三通处的流场进行实验测量,得到了三通涡流区的静压分布特性。Mayurkumar等[6]实验研究了含T型三通的换热器,发现减小传热管直径与增大传热管间距有利于流量分配均匀性,同时联箱直径的增大可能会带来流量分配均匀性的改善或恶化。Zhou等[7]在考虑各几何参数对流量分配影响之间的交叉作用基础上,研究了关键几何参数的影响,并提出了3类分布形式及相应几何尺寸优化方向。

为进一步改善换热器内流量分配均匀性,学者们对换热器结构优化开展了大量研究。Wang等[8-9]对联箱几何结构提出多种改进方案并开展了实验研究,取得了较好的效果。Wei等[10-11]在分配联箱内插入了一个多孔挡板,实现了在并联管组中的目标流量分配,并给出了孔板上孔径的确定方法。Tong等[12-13]模拟研究并提出了多种并联管组改进手段,如线性与非线性渐缩联箱,管口加装阀门等。Said等[14]通过调整入口管直径得到了较为理想的流量分配。但上述方法将带来较大的流动阻力。Zhou等[15]提出采用双入口管、改变入口管插入角及采用弧形三通替代原有T型三通来实现换热器内更为优异的流量分配特性及较小的流动阻力,并进行了数值模拟研究,获得了较好的效果。

现有文献多开展传热管数量较少换热器的研究,对于传热管数目众多、长度较长的工程级换热器研究较为匮乏。同时,此前研究表明换热器各几何结构参数对其流量分配的影响相互作用较强,其结论对于PCS所采用的双区、宽翼展大型换热器的适用性仍不明晰。

因此本文对大型中心型换热器内流量分配特性开展了数值模拟研究,以了解各参数对大型中心型换热器内流量分配特性的影响并为工程设计提供相应指导。

1 数值模型及验证

研究中主要考察换热器内单相水的流动特性,忽略了传热过程。因此,研究中流体流动稳态情况下遵循如下控制方程。

质量守恒方程：

动量守恒方程：

湍流方程：

式中：ui为速度在x、y、z方向上的分量,m/s;ρ为工作介质的密度,kg/m3;p为压强,Pa;k为湍流动能,J;ε为湍动能耗散率。湍流常数σk=1.0和σε=1.3,μt为湍动粘度,经验常数C1和C2分别为1.44和1.92。

模型验证基于Mayurkumar等实验研究中的一例进行[11],几何结构如图1 (a)所示。对比其实验及模拟结果以验证模型的准确性,验证结果如图1 (b)所示。本文模拟结果与Mayurkumar等[11]的实验及模拟结果符合良好,可认为本文使用的模型是准确可信的。

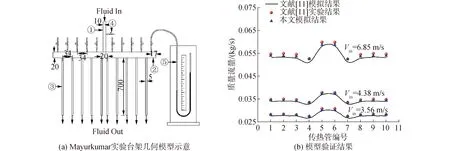
图1 基于Mayurkumar实验及计算结果的模型验证Fig.1 Model verification based on Mayurkumar′s experimental and numerical results

2 模型设置与网格无关性验证

由于中心型换热器高度对称,几何上以换热器三通中轴面为对称平面,仅对半台换热器进行模拟与分析。并对此简化方法进行验证,计算结果表明与对全换热器建模各管流量偏差小于0.5%。几何模型如图2 (a)所示,下方管入口为质量流量入口,上方管出口为压力出口,中心为对称平面,其余均为壁面。几何结构尺寸如图2 (b)所示,传热管内径Dt、传热管中心距Dtp、T型三通两侧最邻近传热管中心距Dpt(简称中心管间距)、联箱内径Dh、传热管高度Ht,传热管采用叉排布置,计算中基准工况传热管中心距Dtp为8.18倍联箱内径Dh。传热管编号如图2 (c)所示,传热管编号起始于最外侧靠近三通位置的传热管,终止于最内侧联箱端部传热管。

图2 几何模型及传热管编号示意Fig.2 Schematic diagram of the geometry and number of heat transfer tubes

计算在常压下进行,工质为80 ℃的水,对应物性参数依据IAPWS-IF97设置为常数。换热器入口质量流量为36.91 kg/s。

网格划分选取多面体网格,管束竖直段采用广义圆柱体进行网格划分,其利于平行管壁流动计算的精度及收敛性,同时能大幅减少网格数量。低流量条件下,棱柱层数划分12层以上并保证壁面y+约等于1,高流量条件下,棱柱层划分2～3层并使得壁面y+在30～300内。管束区网格划分及网格无关性验证结果如图3所示,网格无关性验证图中各网格基本参数见表1。由于换热器体积大、传热管数目多,全尺寸条件下无法进行较宽范围内的网格无关性验证,分别对T型三通部分、传热管竖直段划分段数及2排5列U型换热器内流量分配单独进行大范围网格无关性验证。3个部分网格所需网格尺寸取交集,最终选取网格5作为网格划分方法,传热管竖直段划分100段。

表1 网格基本参数Table 1 Basic parameters of grids

图3 网格划分及无关性验证Fig.3 Grid structure and independence verification

3 计算结果分析

3.1 换热器联箱内典型流动特性

图4展示了汇流联箱及分配联箱内流动特性。图5展示了分配联箱和汇流联箱内沿联箱中心轴线静压分布情况,为更好地反映联箱内静压差的变化趋势,将分配联箱内静压减去重力水头。

图4 联箱内速度矢量分布Fig.4 Velocity distribution in headers

图5 联箱中轴线处静压分布Fig.5 Static pressure distribution at the central axis of the headers

分配联箱内,流体沿T型三通入口管进入联箱并在正对T型三通中心位置处滞止,在此位置会形成静压最高的区域。流体向两侧分流,由于惯性的作用,大部分流体会贴附于分配联箱下侧流动。在流动过程中,由于边界层分离,T型三通两侧处产生了涡流。而涡流占据了一部分流通面积,使得转弯处流速增大,形成一个低压区,在T型三通两侧各存在一个静压极小值,如图5所示。由于流体慢慢分流至各传热管内,联箱内流量逐渐减小,分配联箱内静压慢慢回升。

流体慢慢汇集于汇流联箱内,联箱内流速从端部向T型三通位置处逐渐增大,静压逐渐降低。联箱两侧流体最终在T型三通位置处发生碰撞,该位置联箱中心线处流速降低,从而出现一个较小的静压峰值,并最终汇入T型三通流出换热器。在汇流联箱内并不会形成较强的涡流区。因此,汇流联箱内静压分布较分配联箱均匀。

3.2 倾斜管/竖直管

传热管倾斜布置十分有利于换热器管外含空气蒸汽冷凝换热能力。为此,对比了传热管束倾斜30°与竖直条件下换热器内流量分配情况,结果如图6所示。为更直观地反映各管流量分配情况,以各管内质量流量Gi与管内平均质量流量Gave的比值作为纵坐标。二者流量分配特性相似,靠近T型三通处传热管内流量较高,向联箱端部管内流量缓慢减小。倾斜管束换热器内流量分配均匀性略优于竖直管束换热器,主要原因是倾斜30°管总长度约为竖直管总长度的1.67倍,其管内流动阻力约为竖直管的1.67倍,因此使得流量分配的不均匀性减小。

图6 竖直和倾斜管束换热器内流量分配特性Fig.6 Flow distribution characteristics in vertical and inclined tube bundle heat exchangers

3.3 管列数及中心管间距

对于中心型换热器,T型三通位置会形成较为明显的涡流,在分配联箱T型三通位置会发生静压的骤变,而汇流联箱内静压分布相对较为平缓,因此T型三通及附近传热管两端压差会存在大幅变化,使得三通附近位置流量分配极不均匀[4-5]。故中心管间距对于流量分配特性有重要影响,设计时应避开中心涡流区。不同中心管间距条件下换热器内流量分配情况如图7所示。当中心管间距为0.55Dh时,受三通位置处涡流的影响,三通附近传热管流量分配极不均匀,与管内平均流量最大正偏差高达155%,最大负偏差高达89%。设计上应当尽可能避免T型三通处涡流的影响,对于计算工况,中心管间距大于2倍联箱直径时可较好地避免三通位置处涡流对流量分配的不利影响。特别地,对于计算工况,换热器中心管间距为5.13Dh时,流量分配均匀性比中心管间距为8.18Dh时更好。

图7 不同管列数及管中心距条件下流量分配特性Fig.7 Flow distribution characteristics under various number of tube columns and tube center distances

3.4 弧形三通

一些学者[8-9,14]倾向于用标准方差评价流量分配的不均匀性：

式中：Nt为传热管数目;Gi为各管内质量流量,kg/s;G为换热器总质量流量,kg/s。

Zhou等[15]提出可以采用弧形三通来减小流量分配的不均匀性。定义无量纲弧形半径r/Dh为弧形三通半径r与联箱直径Dh的比值。带有不同弧形三通半径中心型换热器各管流量分配情况如图8 (a)所示,相对不均匀性系数和相对压力损失随无量纲弧形半径的变化如图8 (b)所示。由图8可知,弧形三通半径过小或过大均不利于流量的均匀分配,且弧形三通半径过小(例如与联箱等径)可能会加剧流量分配的不均匀性。r/Dh为1.5时不均匀系数最小。同时,由于弧形三通的导流作用,减少了入口三通位置处流体对三通的撞击及出口三通位置处两侧流体汇流带来的撞击所造成的能量损失,换热器内压力损失较T型三通换热器有明显减小。r/Dh为1.5时,换热器内流动阻力较传统T型三通换热器减小50%,当r/Dh大于1.5后,继续增大弯曲半径,压力损失变化不明显。

图8 不同弧形三通半径条件下流量分配及流动阻力特性Fig.8 Flow distribution characteristics under various radii of curved tee

3.5 联箱直径

引入无量纲参数流通面积比RA和分配联箱与汇流联箱横截面积比RDC,表达式为：

式中：Dt为传热管内径,m;Dh为联箱直径,m;Dd为分配联箱直径,m;Dc为汇流直径,m。

对于等径联箱,不同联箱直径条件下各管内流量分配特性如图9 (a)所示,图例中“-”前后分别代表汇流联箱直径和分配联箱直径,D0为前述计算的换热器联箱尺寸。联箱直径的改变并不会带来流量分配形式的改变,均为中心位置传热管内流量较大。随着联箱直径的增大,联箱内流量分配均匀性整体上逐渐变好,但在联箱直径从1.1D0增大到1.2D0时,联箱内流量分配特性基本一致。即流通面积比RA在3.00～3.52内,流量分配均匀性对联箱尺寸的变化并不敏感。

对于不等径联箱,其流量分配均匀性较等径联箱差。当分配联箱的直径小于汇流联箱的直径时,靠近三通位置处传热管内流量较低,而联箱端部流量较高;当分配联箱的直径大于等于汇流联箱的直径时,流量分配情况与之相反。本文计算RA值约为3,Zhou等[7]得出在RA大于3后,等径联箱流量分配均匀性最好的结论在此仍适用。这主要是由于随着RDC的值增大,中心处传热管内流量随之增加,对于RA大于3时,等径条件下流量分配形式为中心传热管流量较高,当RDC大于1时,RDC的增加会引起中心位置处传热管内流量进一步增大从而使得流量分配不均匀性加剧;当RDC小于1时,RDC减小会造成中心位置传热管内流量迅速减小使得流量分配的均匀性恶化。