盾构隧道开挖过程地表变形分析
2023-07-28张明丽
张明丽
(阜阳市茨河铺枢纽工程管理所,安徽 阜阳 236000)
1 引言
随着我国城市化建设的快速发展,地下空间的利用得到了大幅提高。以隧道为例,隧道在开挖过程中会对周围环境产生影响,导致地表发生变形和沉降,影响隧道的安全运营。目前隧道开挖的方式主要为盾构施工。相比其他方式,盾构法对地层的扰动更小,但不可避免的对周围岩土体造成扰动。因此如何有效地预测和控制隧道施工过程中对地层产生的不利影响,是目前国内外研究的热点和难点。
叶友林和路志旺[1]基于数值模拟研究了沈阳地区砂砾地层浅埋盾构隧道开挖对地表变形的影响,结果表明,拱顶覆土厚度、土体强度对地表变形影响很大,因此合理地进行选取初始注浆弹性模量在一定程度上可改善地表变形。丁静泽和陈建平[2]基于现场变形监测数据和数值模拟研究了武汉地铁隧道地表沉降规律。结果表明,隧道开挖施工过程中地表沉降可分为3 个阶段:分别为初期沉降阶段、快速沉降阶段和沉降收敛阶段,各阶段中快速沉降阶段地表沉降量占总沉降量的67%。孙国庆[3]基于FLAC3D 数值有限元研究了浅埋隧道开挖对地层变形影响。结果表明,隧道的地表沉降均小于10 mm,隧道施工过程较为安全,稳定性较好。马乐民等[4]基于现场监测数据和数值模拟研究了隧道左右线洞口段施工时序对隧道地表沉降的影响。结果表明,地表沉降量受洞口段地形高低、隧道开挖及支护时间等多因素叠加影响。徐新星[5]依托某隧道工程实例,利用有限元软件建立模型进行数值计算,研究了隧道两种断面开挖施工方法引起不同方向的土体变形。结果表明,数值模拟得到的土体变形与实测数据相近,文中提出的地表沉降变形预测模型是合理的。张彪等[6]采用物理模型试验研究了不同桩基长度对隧道开挖地层的变形影响。结果表明,隧道周围土体变形随桩体的长度增大而先增大后减小,中长桩基对于隧道顶部的水平和竖向变形有良好的控制作用。刘俊生等[7]基于数值模拟研究了双线盾构隧道开挖地表沉降变形规律。结果表明,双线盾构开挖相互扰动效应明显,实际施工中应采取支护措施,减小扰动影响。张天奇等[8]基于模型试验和数值模拟研究了砂土隧道开挖引起的地表及深层土体变形规律。结果表明,隧道开挖过程中,隧道周围土体的体积响应与应力路径关系密切,即不同应力路径下的土体体积响应有所不同。
本文基于数值模拟手段研究了盾构隧道开挖过程地表变形规律,分析土体的弹性模量以及厚度变化工况下,地表水平和竖向位移的分布规律。
2 工程概况与数值模型建立
2.1 工程概况
本文研究隧道地处高中山地貌,隧道的最大和最小埋深分别为500 m 和80 m 左右,高程位于940 m~1500 m 之间。地形起伏较大,斜坡坡度介于10°~30°之间。隧址区地层主要由粉质黏土和断层角砾岩为主。地质构造复杂,发育有较多的断裂构造,对隧道施工影响较大。隧道施工主要包括开挖,衬砌和注浆填充。在盾构掘进过程中,应力部分释放,随着衬砌拼装,地应力全部释放并达到稳定。
2.2 数值模型建立
采用FLAC3D 建立隧道开挖数值模型见图1。其中模型的长度为60 m,宽度为40 m。衬砌结构采用Shell 单元模拟,折减系数取值为0.75。衬砌结构与土体采用接触面模拟,其中,接触面参数法向刚度和切向刚度取值分别为Kn=109Pa /m、KS=109Pa/m。岩土体和衬砌结构材料的物理力学参数根据室内土工试验取值,具体见表1。隧道埋深为15 m,外径和内径分别为6 m 和5.4 m。衬砌厚度为0.3 m。岩土体采用摩尔-库伦本构计算。衬砌假定为各向同性弹性体。

表1 岩土体物理力学参数
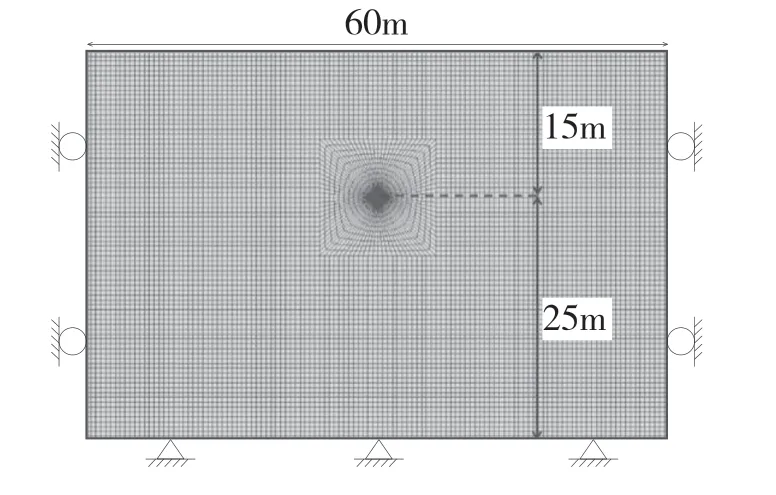
图1 模型有限元网格划分图
本文假定隧道开挖方式为应力释放法[9]。为研究多层土中各层土厚度比值以及各层土刚度比值对地表变形的影响,本文将模型中的土层划分为两层和三层(图2)。各层土的厚度分别表示方法见图2。其中各层土厚度之比定义为厚度比,下文中统一用A 表示,各土层之间的弹性模量比值定义为刚度比,下文中统一用B 表示。
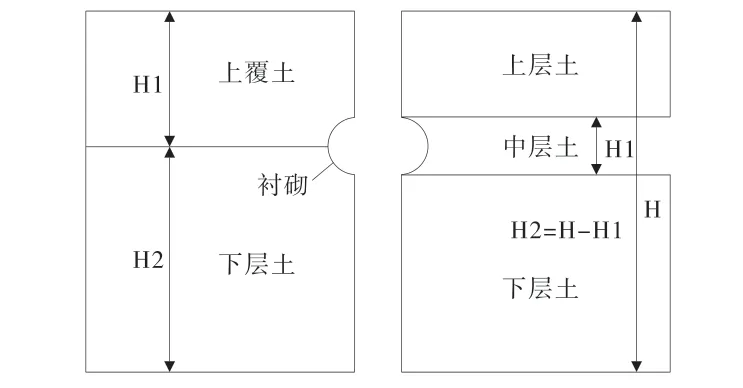
图2 模型有限元网格划分图
3 计算结果与分析
3.1 土层厚度比的影响
图3 汇总得到固定土层刚度比B=0.13 情况下,土层厚度比分别为0.29、0.42、0.6、0.82 和1.11 工况下,地表的水平和竖直向位移分布规律。结果表明,地表水平向位移随距隧道中心距离的增大呈高斯分析形态。当刚度比不变时,厚度比越大,水平和竖向位移越大。当土层厚度比小于0.82 时,水平和竖向位移变化速度比较小,当厚度比为1.1 时,位移显著增大,其最大水平位移为7.1 mm,竖向最大位移为20 mm。总体结果表明,对于较小弹性模量的土层厚度不断增大,土层整体的有效刚度逐渐减小,而较小的刚度导致较大的地表变形。

图3 两层土地表位移分布规律
图4 汇总得到固定土层刚度比B=8 情况下,地表的水平和竖直向位移分布规律。与图3 结果相比。土体的水平向位移和竖直向位移随上层土厚度的增大而减小。且减小幅度明显小于图3 位移增大幅度。水平位移在距隧道中心15 m 处达到最大,最大值为7.5 mm;竖向位移在距隧道中心0 m 处达到最大,最大值为42 mm。导致这一现象的主要原因也可以用有效刚度理论解释,即随着较大弹性模量的土层厚度增大,整个土体的有效刚度增大,从而减小了土体的变形量。此外,由于土体的有效弹性模量对地表的位移影响不同。弹性模量减小导致引起的地表位移大于弹性模量增加而引起的地表位移。因此,即使土层厚度比相同,但由于不同弹性模量的土体层厚度增大或者减小,也会导致地表水平和竖向变形发生差别。

图4 两层土地表位移分布规律
图5 汇总得到固定刚度比B=0.25,三层土层厚度变化工况下地表位移分变化情况。结果表明,地表水平和竖向位移随中间土层厚度的减小而逐渐增大,但增加速率较小,水平和竖向位移曲线近似服从高斯分布曲线。水平位移在距隧道中心15 m 处达到最大,最大值为6 mm;竖向位移在距隧道中心0 m 处达到最大,最大值为17 mm。但由于土层层数不同不会改变地表形态,因此变形曲线都服从相同的分布规律。
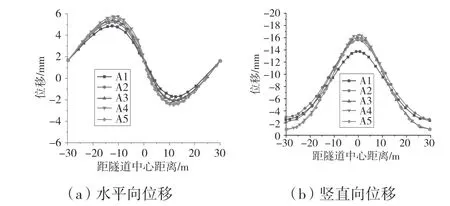
图5 三层土地表位移分布规律
3.2 土层刚度比的影响
图6 汇总得到土层厚度比固定为0.6 时,刚度比变化对地表水平和竖向位移的影响规律。结果表明,当上层土的弹性模量为3 MPa 时,地表水平和竖向位移随刚度比的增大而减小。产生这一现象的原因有两方面:(1)当刚度比改变时,土体的有效弹模增大,进而导致土体的变形减小;(2)隧道开挖对地表变形的影响存在一定的影响范围,在该影响范围之内,隧道周边土体的的变形起到控制作用,随着刚度比减小,控制影响区内的土体弹模增大,土体处于硬化阶段,隧道地表水平和竖向位移减小[10]。
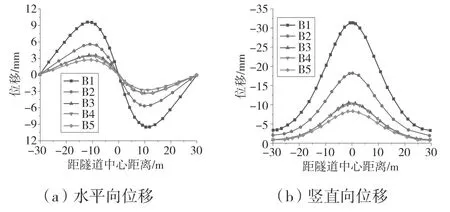
图6 两层土地表位移分布规律
4 结论与建议
本文基于FLAC3D 数值有限元,在平面应变的假定条件下,建立数值有限元模型,计算并分析了土层厚度比变化和土层刚度比变化对地表水平和竖向位移的影响,得到如下结论:
(1)当刚度比较小且保持不变时,地表水平和竖向位移随厚度比的增大而增大;当刚度比较大且保持不变时,地表水平和竖向位移随厚度比的增大而减小,造成结论相反的原因是由于刚度比不同导致土体的有效弹性模量改变,进而导致地表位移发生改变。
(2)对于三层土情况,盾构隧道施工对地表变形的影响仍然受有效弹性模量和影响区的控制。但无论何种情况,地表位移曲线均呈现出高斯分布形态。
(3)根据本文的研究,隧道施工过程中需关注影响区范围对地表变形的影响,建议在隧道周围增加地表变形监测仪器,随时关注地表变形动态变化;隧道开挖过程中及时进行衬砌拼装和注浆加固处理。
