均质土石坝稳定性分析及加固方案研究
2023-07-28吴奇峰
吴奇峰
(赫章县水务局,贵州 赫章 553200)
0 引言
随着我国现代化的发展,我国发达区域对水资源和用电的需求在不断增大,在我国西部采用水坝发电已经成为大势所趋。但在我国西部,水坝的建设需要克服许多复杂的地理环境,其中水坝抗震能力尤为重要[1-2]。
国内有诸多学者研究了土石坝的加固方案,其中在坝体1/4 高度处进行加固被证实为十分经济有效的措施之一[3-4]。但在已有研究中采用土工格栅[5]与数值模拟结合[6],预测加固结果的研究还尚属少见。
本文选择位于某省赫章县深沟水库土石坝进行研究,采用有限元对文中涉及的堆石坝进行建模计算,讨论加筋前后土石坝在动荷载的作用下其动应变、动态加速度、和动应力与动力时程间的变化关系,为实际工程提供指导意义。
1 土工格栅加筋计算原理
土工格栅多采用高分子材料制成,如密度很大的聚乙烯等。高分子材料在加热后通过挤压、打孔、冷却等工艺定型成为格栅状。在土石混合物中加入土工格栅,可以通过限制土石颗粒的位移增加颗粒间的咬合力和表面摩擦力,总而达到增大土石构筑物力学强度的目的。挡土体和石块的滑动位移受到限制后,变相的增大了土石颗粒间的粘聚力,大大提高了构筑体的稳定性。目前学者的研究表明土工格栅增强构筑体的稳定性主要原因有二,一是利用了颗粒间的摩擦力达到加筋的目的,二是限制颗粒间位移,增大了粘聚力。
根据已有研究结论发现,对加筋土与未加筋土体进行三轴剪切试验,比较试验结果发现未加筋土体的正应力与主应力在围压的作用下达到了极限平衡状态;而加筋土在相同的受力条件下未达到极限受力平衡状态,并且仍处于弹性变形的阶段,这一实验结果说明土体在加筋后力学强度有显著的提高。
2 计算方法
2.1 坝体建模
本文选择位于某省赫章县深沟水库土石坝进行研究。大坝的主体由砾石和黏土堆砌而成,为典型的碾压土石坝。大坝上游和下游的坡度比为1∶2,最大坝高为27 m,坝顶的最大宽度为5.1 m。大坝的心墙为土石墙,坝底宽度127 m,心墙顶端最大宽度6.5 m,坡比为1∶2。心墙的上游和下游分别设置了不同厚度的反滤层和过渡层,过渡层的厚度为22 m。土工格栅设置在顶区域,具体位置见图1(a)。土工格栅采用平铺的方式对坝顶向下6 m~50 m 范围进行加筋防护,格栅置于砾石层内,不埋设在过度层和反过滤层之内,土工格栅的最大分布间距为2.5 m。
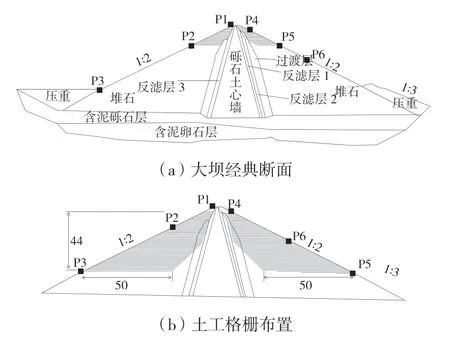
图1 加筋坝体典型剖面图
本文采用有限元对文中涉及的土石坝进行建模计算,在建模过程中将采用相同的区域作为一个整体模块,便于在进行模拟计算时进行静力分析和附件参数值。在进行土石坝的抗震计算分析时,假设土工格栅在发生破坏时承受极限抗拉强度等值的力学强度,加筋后的土石构筑体在模型中仅以堆石的外观出现,在进行分析计算时,对加筋后的堆石坝体附加粘聚力数值,但内摩擦角与普通未加筋堆石坝保持一致,模型见图1(b)。
2.2 地震波
大坝在设计时采用的水平向基岩加速度最大值为0.401 g,这一数值超过规定数值的2%,本文在进行杜正波模拟时采用水平行向与竖向双向输入的方式进行,但是地震波的加速度仅设置为最大加速的的66%,采用相同的相位进行振动的施加,沿河床方向的振动加速度时程变化曲线见图2。

图2 振动加速度时程变化曲线
2.3 土工格栅抗拉强度
本文选用的土工格栅的最大抗拉强度超过260 MPa,纵向最大抗拉强度超过160 kN/m,极限状态下延伸率可达8%。考虑到在施工过程中物理损伤和性能削减,文中调整土工格栅的最大可变性能力为7%,定义纵向的单条最大抗拉强度为100 kN/m,综合上述分析,最终选用单条SR-55 土工格栅,其具体的参数为:肋条宽度最小为6 mm,平均厚度1 mm,横肋最大宽度为15 mm,纵肋平均长度为160 mm,最大网孔宽度为15 mm,出厂弹性模量约3.8 GPa,随应变的增大弹模逐渐减小。单条SR-55 土工格栅的纵向拉伸试验结果见图3。

图3 土工格栅的纵向拉伸试验结果
在进行对加筋土石坝模拟计算时采用等效附加原理进行数据分析。在进行模拟计算时假设水坝是处于蓄满水的状态,并将整个坝体的应力计算过程划分为14 个区域,及将构成坝体的材料分为14 层填筑,水库的蓄水过程也分为3 个阶段。水坝处于正常蓄水为时,水位以下部分的坝体材料采用浮密度计算附加值,在模拟计算过程中忽略水在坝体中的渗流作用对计算结果的影响。在施加动荷载后,进行动力学计算时,将覆盖坝体的材料均采用等效粘弹性动力学本构模型进行代换。在计算过程中将土石构筑体当做弹性体进行分析,并在计算模型中引入阻尼比λ和等效弹性模量两个参数来表达土石构筑体在动荷载的作用下,动应变与动应力之间的变化关系。采用等效替代法获取的计算应变函数的自变量与应变量之间多表现出非线性变化的关系。根据这一关系,将土石构筑体的动应变化简化为动剪应力τ和动剪应变γ,发现这两者存在双曲线的变化关系,其表达式为:
这样土石坝的动弹性泵后模型就可以采用双曲线的形式表达。根据加筋后土石坝的动弹性试验可以发现,通过最大的动剪切模量和阻尼比的变化可以反映出在动力试验过程中动应力与动位移的变化关系。采用等价线性法对试验数据进行分析发现,与未加筋的土石坝相比,加筋后土石坝的最大剪切模量增大了6%。
3 试验结果
3.1 坝体动力反应分析
当水坝处于正常蓄水水位时,对土石坝进行动响应试验.水平向位移与竖直向位移均为大坝水位线位于正常水位的计算结果。通过比较可以发现大坝水位线位于正常水位后水平向位移与竖直向位移对应的动应力和位移值基本一致。坝体心墙最大沉降发生在距离大坝顶端向下约1/3 的位置,并且出现在大坝上游的位置,有向着下游发展的趋势。在大坝上游水压的作用下,坝体内部的水平位移水流的方向向下游呈增大趋势,最大水平位移出现在距离大坝顶端向下约1/2的位置,且出现在大坝上游的位置。加筋后土石坝的最大动内应力有所下降,答题的应力分布趋势和位置没有变化,在坝体的上游侧出现了小范围的受力变形区域。
模拟计算过程中的动荷载,分析加筋前后土石坝在动荷载的作用下其动应变、动态加速度、和动应力与动力时程间的变化关系曲线,由图1(a)在坝体的上游和下游各布置了3 个检测点位,分别是上游P1、P2、P3,和下游P4、P5、P6,具体点位分布如图1(a)所示。
通过有限元的计算结果分析得出,采用土工格栅对土石坝进行加筋,施加动荷载后加筋前后的土石坝加速度和动态位移基本没有差别。图4 中给出了P1 监测点在加筋前和加筋后的水平向动态位移变化曲线。比较6 个监测点的变化曲线可知,由于坝顶的“鞭鞘”效应,使得坝顶以下区域在动态荷载的作用下,其动态加速度和动态位移仅表现出坝高越高加速度越大的变化趋势。由图4 可知,P1 监测点的水平加速度最大值增大了3.89 倍,水平位移最大值为48.1 cm;P5监测点的竖直向加速度最大值增大了3.93 倍;竖直向位移最大值为13 cm,发生在P2 监测点。
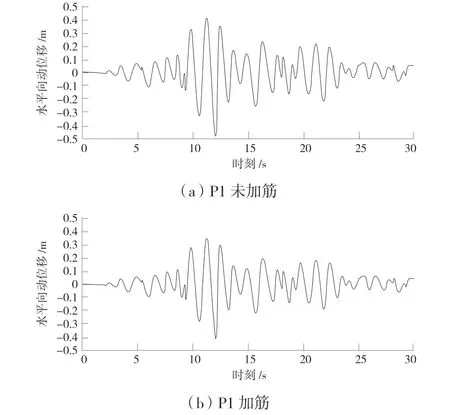
图4 P1 监测点在加筋前和加筋后的水平向动态位移变化曲线
将6 个监测点的动应力用下时程曲线叠加处理,分析比较加筋前后土石坝的动态时程变化情况。观察P2、P4、P5等三个监测点可以发现,加筋处理后土石坝在承受动态力的初始时刻的静力平衡转态的应力要大于加筋之前,这一变化导致叠加后的时程数值在加筋后要大于加筋之前。但对于动应力变化而言,加筋并未从总体方面提高土石坝基体的动态受力表现。位于非加筋区域的监测点,动应变的时程叠加未受到加筋区域的影响。图5 中展示了加筋前后P2 和P6 监测点正应力时程叠加变化曲线。


图5 加筋前后P2 和P6 监测点正应力时程叠加变化曲线
综上所述,对土石坝进行加筋处理,在受到动态荷载作用时,加筋部分动应力的提高主要是由于在静态受力过程中堆石弹性模量增加导致的。
3.2 格栅受力分析
将图1(b)中中埋入堆石的土工格栅进行排序编号,进行分析,上游的栅格编号为1~23,下游的栅格编号为24~46。图6 中展示了在动态荷载后各个编号土工格栅的动应变最大值。由图6 可知,位于土石坝下游的土工格栅随着铺设高程的降低,土工格栅承受发生的应变逐渐增大,其中46 奥格栅发生的动应变最大为0.15%。在土石坝上移,动应变最大处发生在编号为14 的土工格栅,最大动应变为0.11%,并且编号14 以下的格栅动应变逐渐减小。
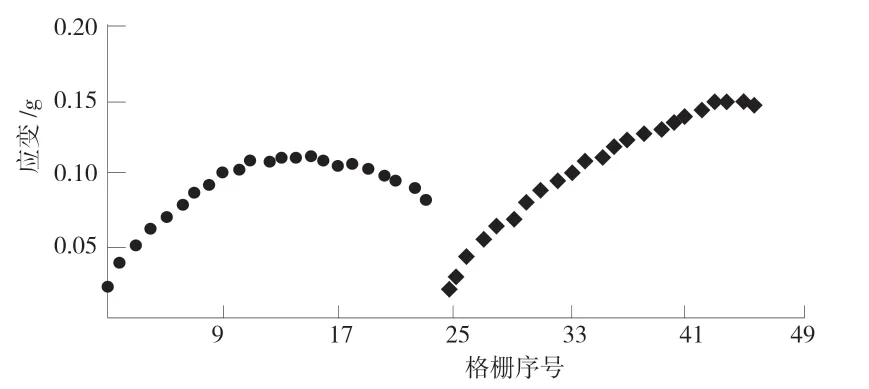
图6 各个编号土工格栅的动应变最大值
在动荷载的作用下,发生动应变的各土工格栅的应力最大值曲线见图7。由图7 可知46 号格栅和14 号格栅承受了土石坝两侧最大的拉应力,分别为1.3 kN/m 和0.9 kN/m。综合比较可以看出,在土石坝受到动荷载作用时发生的动应变要远小于土工格栅的极限协调形变值7%,同时也可以发现,土工格栅承受的最大拉力要远小于100 kN/m,因此次加固方案完全可以满足文中土石坝的加固。
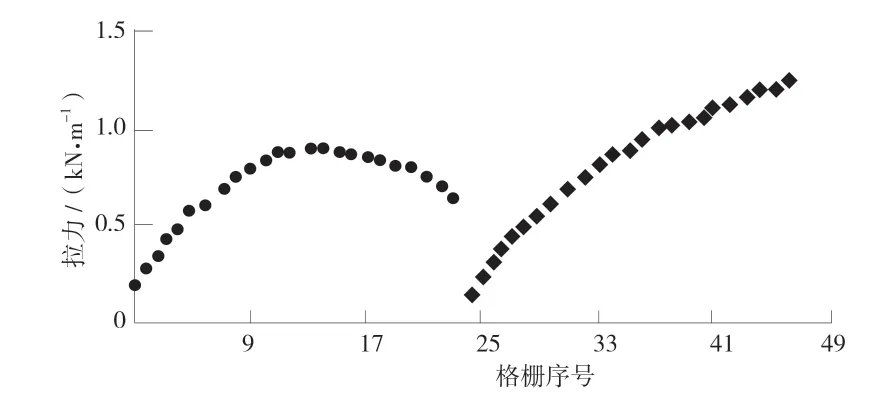
图7 土工格栅的应力最大值
4 结论
本文采用有限元对文中涉及的土石坝进行建模计算,分析加筋前后土石坝在动荷载的作用下其动应变、动态加速度、和动应力与动力时程间的变化关系,研究结果表明:
(1)由于坝顶的“鞭鞘”效应,使得坝顶以下区域在动态荷载的作用下,其动态加速度和动态位移仅表现出坝高越高加速度越大的变化趋势。
(2)加筋处理后土石坝在承受动态力的初始时刻的静力平衡转态的应力要大于加筋之前,这一变化导致叠加后的时程数值在加筋后要大于加筋之前。但对于动应力变化而言,加筋并未从总体方面提高土石坝基体的动态受力表现。
(3)综合比较可以看出,在土石坝受到动荷载作用时发生的动应变要远小于土工格栅的极限协调形变值7%,同时也可以发现,土工格栅承受的最大拉力要远小于100 kN/m,因此次加固方案完全可以满足文中土石坝的加固。
