宽带太赫兹超表面带通滤波器

亓丽梅,陶 翔,罗 淘,杨 君

(北京邮电大学 电子工程学院,北京 100876)

1 引言

超表面在太赫兹波段具有很强的电磁响应,从而在太赫兹功能器件的设计中得到了广泛关注[1-9]。基于超表面的太赫兹带通滤波器在光谱成像和传感等方面都有重要应用[10-14]。超表面太赫兹带通滤波器通常采用金属-介质-金属的三层三明治结构。J. Han等采用三层超表面设计得到3 dB带宽为29%宽带带通滤波器[15]。Y. Chiang等加工并测试得到在中心频率1.25 THz范围内超过50%的滤波器传输宽度可达0.5 THz[16]。M. Lu等测试得到带通滤波器2 dB插入损耗的频率范围为0.227～0.283 THz[17]。F. Lan等设计并测试得到带通滤波器3 dB带宽为0.3～0.324 THz[18]。L. Qi等通过实验得到了一个双波段带通滤波器,滤波器中心频率分别位于0.35 THz 和0.96 THz,对应3 dB带宽分别为31%和17%[19]。J. Li等采用双层频率选择表面实现了一个3 dB带宽为0.4 THz的滤波器[20]。J. Huang等设计了金属-二氧化钒-介质-金属-二氧化钒五层结构的可调宽带带通滤波器,通过改变二氧化钒实现了带宽为0.32 THz的可调带通滤波器[21]。

以上研究的超表面带通滤波器,通常采用表面电流和电磁场分布和电路模型进行物理机理分析,并且3 dB相对带宽都没有超过50%。本文设计了一款超宽带三明治结构太赫兹带通滤波器,测试得到滤波器3 dB带宽为56.6%,通过调研未见超过该相对带宽的超表面滤波器结构。此外,为更好描述滤波器的物理模型,本文分别采用耦合模理论[22-24]和多重散射理论模型[25-28]进行了建模。两种理论模型的计算结果与模拟和测试一致,从而说明了模型的正确性。这两种理论模型为进一步设计多层宽带太赫兹带通滤波器提供了重要指导。

2 结构设计及结果

图1给出了设计的金属-介质-金属结构的三层带通滤波器示意图。其中图1(a,b)分别为5×5周期单元和一个周期单元的结构示意图。该周期结构是在镀金属膜的介质基底两侧构造完全对称重合的金属图形。金属图形构成如下:在金属表面构造正方方环,方环四角沿瞬时针方向分别进行延伸,形成手性图形,通过参数优化,发现该结构图形具有明显的宽带滤波特性。实验加工中,介质材料采用相对介电常数和损耗正切分别为εr=4.41和tanδ=0.004的石英。金属采用电导率σ=3.72×107 S/m,厚度为200 nm的铝。周期结构的参数在图1(b)中进行了标注,对应值分别为p=230,w=130,G=30,L=180和d=120(单位均为微米)。模拟采用了CST仿真软件,其中x,y方向采用周期边界条件,z方向采用了开放边界条件。

图1 太赫兹宽带超表面滤波器(a)5×5周期单元和(b)一个周期单元示意图;(c)加工样品的电子显微镜图;和(d)滤波器的模拟值和有、无氮气填充时的测试曲线图

平面电磁波沿z向入射,可分为电场方向沿x方向的TE波和电场方向沿y方向的TM波。图1(c)给出了加工样品的电子显微镜图。该样品通过标准的光刻技术进行制作,首先在石英的一侧旋涂光刻胶并进行紫外曝光,将曝光后的石英基板进行显影,用去离子水进行冲洗,去掉不需要的光刻胶。然后,采用电子束蒸发法在石英基底上沉积金属铝,最后,将镀有铝膜的石英基板置于光刻胶剥离溶液中进行剥离,形成单面光刻的金属铝结构。另一侧采用相同方式进行光刻。需要注意,在掩膜版制作过程中需要做好对准标记,使得上下两面的光刻图形对齐。测试时采用太赫兹时域光谱技术。太赫兹波受大气中含水量的影响很大,超净间中空气的湿度一般超过20%,如果直接进行测试,太赫兹波在传输过程中损耗很大,为防止水分对测试结果的影响,样品放在充有氮气的密闭容器中进行,通过填充氮气,可使得空气的含水量低于5%。为了比较水分对测试结果的影响,我们对未填充氮气和填充氮气环境下的样品进行了测试。测试结果如图1(d)所示,可见,模拟和填充氮气时的测试结果基本一致,其中测试得到的3 dB带宽为56.6%,对应的中心频率为0.344 THz。当未填充氮气时,传输曲线的损耗明显增大,通带范围的损耗幅度大约下降10%。从而进一步说明了水分对太赫兹的吸收还是比较明显的。为了进一步说明所设计的太赫兹带通滤波器的超宽带特性,表1给出了已报道的相关太赫兹滤波器中心频率、3 dB相对带宽和结构组成的参数对比,可见,本论文提出并测试得到3 dB带宽为56.6%的滤波器在相同结构的滤波器中具有非常明显的宽带特性。

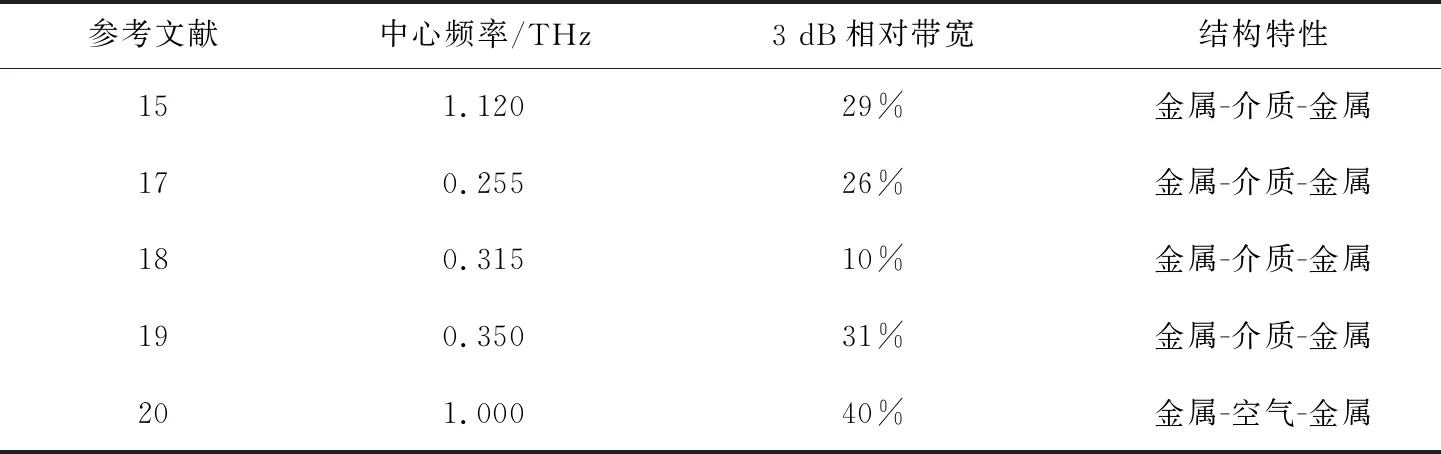
表1 太赫兹带通滤波器结构

3 理论模型

现有文献对金属-介质-金属带通滤波器的物理机理分析,大多数是利用仿真软件对滤波器的电磁场分布特性进行分析,M. Lu等采用电路模型对滤波器的特性曲线进行了拟合和说明[17],本文将分别采用多重散射理论模型和耦合模理论两种理论模型对设计的宽带滤波器进行建模分析,发现这种金属-介质-金属带通滤波器的物理机理可分别采用这两种理论模型进行拟合。

3.1 多重散射理论模型

图2(a)给出了三层结构滤波器的多重散射理论模型,其中,表面两侧的金属图形结构看做厚度可忽略的金属薄膜,当电磁波入射到左侧表面时,一部分电磁波被反射回来(称为0阶反射波),一部分电磁波穿过介质后,通过第二层金属薄膜继续传输的波称为一阶透射,被第二层金属反射回来的波经过中间介质后,又有一部分穿过第一层金属薄膜,称之为一阶反射。由于电磁波不断在三层结构中来回多次反射和透射,从而会出现二阶反射、透射波,和n阶反射和透射波。图2(a)采用电场对多重散射特性的物理过程进行了描述。由于带通滤波器多重散射理论的表达式与常见的超表面吸波器[22-24]和超表面非对称交叉极化器[25-28]的表达式不同,我们进行了公式推导如下。

当电场沿x方向入射时,第0阶和第1阶透射波在x方向的传输分量可以表示为[25,27,29]

(1)

(2)

Ex0=A·B·e-iβd,

(3)

Ex1=A·M·B·e-i3βd,

(4)

于是,得到第n次传输的电场表达式为

Exn=A·M·B·e-i(2n+1)βd,

(5)

此时,x方向的总透射Txx可以写作

(6)

同样,对于y极化波,总传输幅度Tyy可以表示为

(7)

Eyn=A′·M′·B′·e-i(2n+1)βd,

(8)

图2(b)给出了采用多重散射理论模型得到的滤波器传输曲线Txx(点划线)和CST模拟结果(实线)的对比,可以看出两者一致性好。图3给出了滤波器在通带频率f1=0.267 THz和f2=0.408 THz处,电场随多重散射阶数n不同而变化的结果。其中x轴和y轴分别对应电场的实部和虚部,n=0,1,2和3分别代表电场Exn第n次的透射阶数。红线代表n次散射叠加的总和,可以看出在两个频率点处,随着n次数的增加,透过的电场幅度减小,但总透射场增大。其中,对于通带频率f1=0.267 THz的结果,第一次透射电场幅度最大,第二次透射场减小为第一次场长度的一半以上,第三次透射的总场为第二次透射场长度的三分之一,第四次减小为第三次的四分之一以上,第五次透射场的幅度非常小。可见透射总场的幅度主要由前四次的结果决定。对于通带频率f2=0.408 THz透射的结果。第一次透射电场幅度最大,第二次透射总场减小约为第一次长度的四分之一,而第三次透射的总场为第二次透射场长度的五分之一,第三次的透射场幅度非常小,透射总场的幅度主要由前三次的结果决定。因此,随着透射阶数的增大,对应的高阶透射场幅度变小,但总的透射场呈增大趋势,但主要由前四次的结果决定。

图2 (a) 太赫兹宽带带通滤波器的多重散射模型;(b) CST模拟及多重散射模型得到理论曲线比较

图3 同极化传输波随多重散射次数的变化曲线(a)f1=0.267 THz;(b)f2=0.408 THz

3.2 耦合模理论模型

采用耦合模理论得到带通滤波器的物理模型如图4所示,该三层滤波器结构可以看作带有两个端口的谐振腔,谐振腔端口1和端口2对应的两个谐振频率通过耦合系数k进行耦合,a1和a2随时间变化的幅度可以描述为[30, 31]

(9)

(10)

当f1=f2=f,Γ1=Γ2=Γ,Γ1a=Γ2a=Γa,上式进一步化简为

(11)

式中f-=f1-κ=f-κ,f+=f2+κ=f+κ为本征模。Γ-=Γ1+X=Γ+X,Γ+=Γ2-X=Γ-X为吸收因子。下标+和-分别代表对称模式和非对称模(d1+=d2+)(d1-=d2-),Γa代表吸收。

传输系数可以表示为

(12)

采用公式12得到的耦合模对应的传输曲线如图4(b)所示。与模拟结果相比,耦合模理论也能很好地描述这类滤波器的传输特性。对用的耦合参数见表2。

图4 太赫兹滤波器(a)耦合模理论模型;(b)CST模拟与采用耦合模型得到的理论曲线对比

表2 基于耦合模理论得到的参数值

4 结论

本文设计并验证了一个中心频率位于0.344 THz的太赫兹超表面超宽带带通滤波器,测试得到3 dB 对应的相对带宽为56.6%。与常见的采用表面电流和场分布解释,以及电路模型分析的物理机理不同,我们采用了多重散射理论和耦合模理论两种理论模型对设计的带通滤波器结构进行了拟合,计算结果与模拟、测试一致,其中基于多重散射理论推导了与模型对应的多重散射传输方程。本论文采用的两种理论模型与测试吻合的结果将为多层宽带带通滤波器的设计和应用提供重要指导,该方法也可以进一步扩展到微波和光波段。