Square cavity flow driven by two mutually facing sliding walls
2023-07-24BoANJosepBERGADWeiminSANGDongLIMELLIBOVSKY
Bo AN ,Josep M.BERGADÀ ,Weimin SANG ,Dong LI ,F.MELLIBOVSKY
1School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
2National Key Laboratory of Science and Technology on Aerodynamic Design and Research, Xi’an 710072, China
3Key Laboratory of Icing and Anti/De-icing, China Aerodynamics Research and Development Center, Mianyang 621000, China
4Department of Fluid Mechanics, Universitat Politécnica de Catalunya, Barcelona 08034, Spain
5Department of Physics, Aerospace Engineering Division, Universitat Politécnica de Catalunya, Barcelona 08034, Spain
Abstract: We investigate the flow inside a 2D square cavity driven by the motion of two mutually facing walls independently sliding at different speeds.The exploration,which employs the lattice Boltzmann method (LBM),extends on previous studies that had the two lids moving with the exact same speed in opposite directions.Unlike there,here the flow is governed by two Reynolds numbers (ReT,ReB) associated to the velocities of the two moving walls.For convenience,we define a bulk Reynolds number Re and quantify the driving velocity asymmetry by a parameter α.Parameter α has been defined in the range and a systematic sweep in Reynolds numbers has been undertaken to unfold the transitional dynamics path of the two-sided wall-driven cavity flow.In particular,the critical Reynolds numbers for Hopf and Neimark-Sacker bifurcations have been determined as a function of α.The eventual advent of chaotic dynamics and the symmetry properties of the intervening solutions are also analyzed and discussed.The study unfolds for the first time the full bifurcation scenario as a function of the two Reynolds numbers,and reveals the different flow topologies found along the transitional path.
Key words: Two-sided wall-driven cavity;Velocity ratios;Transitions;Flow topology;Energy cascade
1 Introduction
A systematic research on the transitional dynam‐ics of several 2D wall-driven cavity flows was per‐formed in several previous studies (An et al.,2019,2020a,2020b).In particular,we took into consider‐ation the flow within a square enclosure driven by the tangential motion of two opposing walls,with equal speed,in parallel and anti-parallel directions.As the driving velocity of the top and bottom walls had al‐ways the same magnitude,the problem was either re‐flection-symmetric with respect to the horizontal plane,or possessed a triad of symmetries including reflec‐tion with respect to any of the two diagonals and πrotational invariance.In both cases,the reflection symmetries involved were shown to break at the first Hopf bifurcation.
For the classic lid-driven cavity flow (α=0),the appearance of the Hopf bifurcation was found at Reyn‐olds number(An et al.,2020b),which was in good agreement with benchmark literature re‐sults,with estimations for the advent of time depen‐dence at Reynolds numbers 8108.2±0.6 (Auteri et al.,2002),8026.7 (Boppana and Gajjar,2010),8025.9(Kalita and Gogoi,2016),and 8051.0 (Nuriev et al.,2016).Non et al.(2006) investigated the first bifur‐cation in a spanwise extended square cavity,and they found out that the Hopf bifurcation occurred at a much lowerwithλthe wave number.
Square cavity flows driven by two or more walls have been considered in the literature to some ex‐tent.Perumal and Dass (2011) employed the lattice Boltzmann method (LBM) to prove the multiplicity of stable steady solutions that arise when two adjacent walls move away from their connecting corner at equal speeds.The new coexisting solutions broke the reflec‐tion symmetry about the diagonal.Something similar,this time breaking the symmetry with respect to the two diagonals and keeping the invariance to π-rotation,was shown to happen for square cavities with four moving walls,when all pairs of adjacent walls either converged or diverged at the same rate.Prasad and Dass (2016) unveiled,using a high-order compact scheme,multiplicity of steady solutions also for the case of two facing walls moving in anti-parallel fash‐ion.Symmetry-breaking pitchfork bifurcationswere detected at=983.5 and 3203.0.For the par‐allel sliding wall case,Lemée et al.(2015) found a similar result for the pitchfork bifurcation,but they extended the analysis to higher values of the Reyn‐olds number and detected a Hopf bifurcation of the asymmetric state at=10750±250.For the anti‐parallel case and using an upwind compact difference scheme applied to the stream function formulation,Yu and Tian (2018) detected the steady state multiplic‐ity and the pitchfork bifurcation at about the same value of the Reynolds number=3200.Yang and Zhang (2012) set the focus on the capability of the conservation-element-solution-element (CE/SE) method for resolving both corner and off-corner vortices at low Reynolds numbers,and they evaluated the flow inside the two-sided cavity with anti-parallel motion of the top and bottom walls.
All the aforementioned research on square cavi‐ties with two or four moving walls prescribed the same speed to them all.As a result,the flow presented sym‐metries and could only be evaluated as the sole func‐tion of one parameter,the Reynolds numberRe.The results obtained for the symmetric problems set the stage for tackling more complex flow dynamics sce‐narios by taking into consideration a second parameter to introduce an asymmetry through applying different velocities to each one of the moving walls.Hammami et al.(2018) made a first step in this direction by study‐ing the flow in rectangular cavities of varying aspect ratio 0.25≤A≤1.00 (A=H/L,His the height of a square cavity,andLis the bottom side of a square cavity)driven by the independent motion of two-sided walldriven cavity flow with various values of the velocity ratio 0.250≤β≤0.825 (β=V/U,Uis the driving velocity on the lid andVis the driving velocity along the verti‐cal side).Their focus was placed on the bifurcation phenomena and,in particular,on the first Hopf bifur‐cation.Shankar and Deshpande (2000) presented an overview on the fluid mechanics in the lid-driven cavity for 2D and 3D geometries with different aspect ratios through experiments and numerical simulations,in which,the corner eddies,longitudinal vortices,nonuniqueness,transitions,and turbulences were discussed in detail.Albensoeder et al.(2000),Albensoeder and Kuhlmann (2002),and Romanò et al.(2017,2020)did a tremendous work on the two-sided lid-driven cavity flow for both parallel and anti-parallel wall mo‐tions.Both 2D and 3D geometries were considered for research on the linear stability,flow topology,and Lagrangian chaos.Speaking of the Lagrangian chaos,some studies (Franjione et al.,1989;Iwatsu et al.,1989;Leong and Ottino,1989) should be mentioned as well,which are different from the present study,where the Eulerian chaos is concerned.
Despite the considerable amount of work done on the classic lid-driven cavity flow,little effort has been devoted to understanding the flow dynamics in‐side a 2D square cavity driven by the parallel motion of two mutually facing walls with different velocities.This difference in driving conditions has a subtle im‐pact on the transitions,which has been inspired by previous research.To the best of our knowledge,the transition mechanisms underlying slight disruption of the problem symmetries have not been addressed.Our results are,in this sense,novel,and may help under‐stand the effects of imperfect symmetries in this and many other problems.Here we undertake a thorough systematic analysis of this problem,with special atten‐tion in regards to the first Hopf and Neimark-Sacker bifurcations,the onset of chaos,the symmetry disrup‐tion,and the energy cascade,which serve to link the different vortical structures that appear in the flow to their corresponding frequency peaks and associated energy.Since the present study is an extension of authors’ previous work,the in-house code validation and the resolution study will not be repeated in the present manuscript,but can be found in our previous work (An et al.,2019,2020a,2020b).
The outline of the paper is as follows.In Section 2,we address the mathematical formulation and numeri‐cal methods used.Results are presented in Section 3,alongside with a discussion.Finally,we summarize the main findings in Section 4,where the impact of the second parameter,the top-to-bottom velocity ratio,on the flow transitions is addressed in detail.The flow field evolution is analyzed and discussed as well.Concluding remarks are also given in Section 4.
2 Mathematical modelling and numerical approach
Considering the flow of an incompressible Newto‐nian fluid of kinematic viscosityνinside a square cav‐ity of sideL,driven by the independent sliding of the top and bottom walls at constant speedsUTandUB,respectively (Fig.1a),the Reynolds numbers defined for the top and bottom lidsReTandReBtake the form:
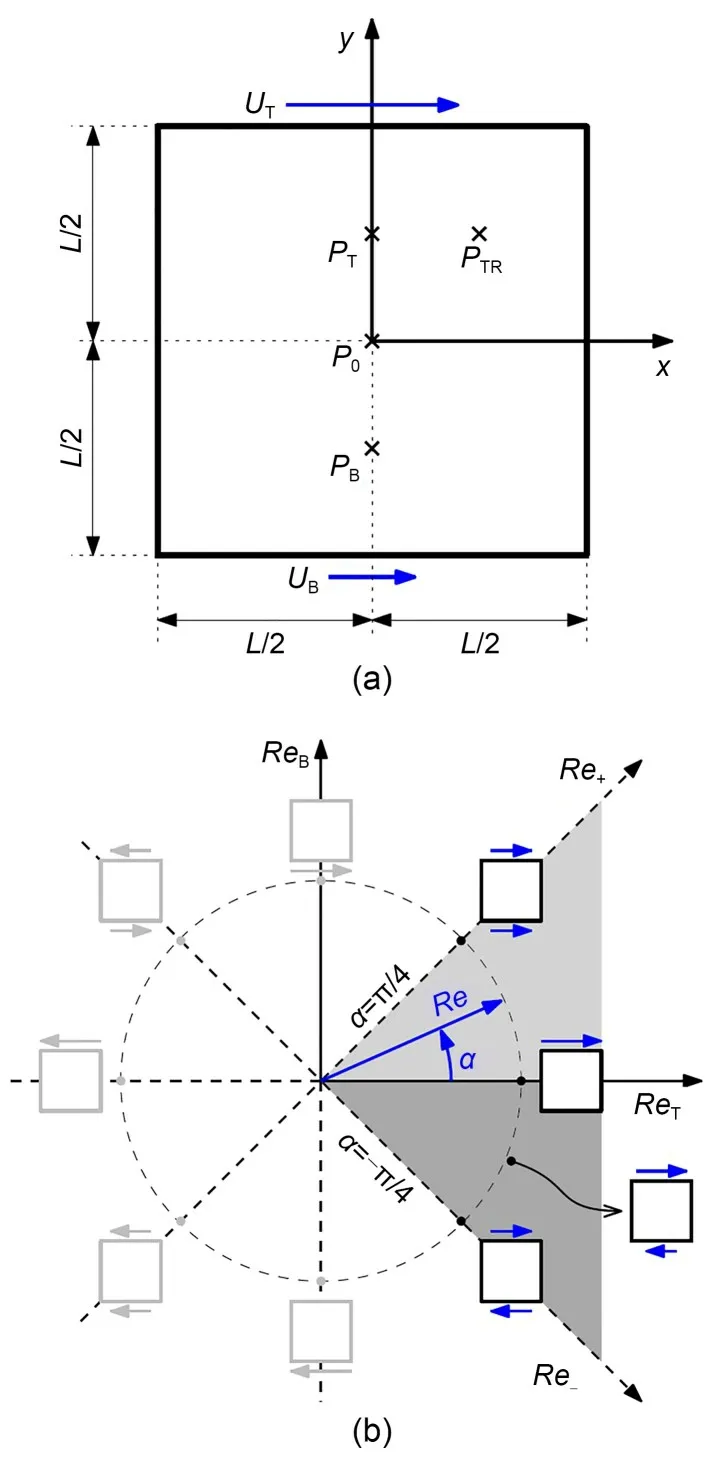
Fig.1 Two-facing-wall-driven square flow: (a) domain;(b) parameter space
In order to make the symmetry disruptions ex‐plicit,it is more convenient to describe the motion of combined top and bottom lids using an alternative set of parameters:
which is equivalent to exploring the 2D Cartesian pa‐rameter space (ReT,ReB) in polar coordinates (Re,α)(Fig.1b).The unique velocity that goes into the bulk Reynolds numberReis related to the top and bottom velocities asUT=UcosαandUB=Usinα.
The dynamics of a Newtonian fluid is governed by the Navier-Stokes equations,which,after nondimensionalisation with length and time scalesLandLU,read as
with unknownsu(r,t)=(u,v) andp(r,t),the nondimensional velocity and pressure fields,respectively,at non-dimensional space coordinatesr=(x,y),x∈[−0.5,0.5],y∈[−0.5,0.5],and advective timet≥0.The coordinate origin has been set for convenience at the centre of the cavity.The boundary conditionsfor velocity are non-slip homogeneous for the left and right walls [u(±0.5,y,t)=(0,0)] and prescribed con‐stant velocity for the top [u(x,0.5,t)=(cosα,0)] and for the bottom [u(x,−0.5,t)=(sinα,0)] walls.Homo‐geneous Neumann boundary conditions for pressure are applied on all walls.
The two-opposing-wall-driven square cavity flow problem is invariant under some sort of symmetry operations (Eq.(S1) in the electronic supplementary materials (ESM)) and can be expressed in terms of the pair (Re,α).The symmetries read as whereMxandMyare the mirror symmetries with re‐spect to the horizontal and vertical mid-planes,respec‐tively,and Rπis the π-rotational symmetry.
As a consequence,only the rangeneeds to be explored,as any value ofαcan be mapped onto the right-angle sector by the appropriate application of a suitable combination of any two of the three sym‐metries.In other words,any case (ReT,ReB) has an equivalent withReT≥|ReB|,implying -ReT≤ReB≤ReT,orRe+≡ReT+ReB≥0 andRe-≡ReT-ReB≥0.There are several ways to achieve this.For instance,Re+might be forced to be positive by application,if required,ofMy,which restricts parameter space to the half planeα∈[−π/4,3π/4].Then,if not already so,the resultingRe-might also be brought to be positive by application ofMx,further restricting parameter space to just the quadrantα∈[−π/4,π/4] (shaded region in Fig.1b).After due mapping,α=0 represents the clas‐sic lid-driven square cavity flow,whileα=corre‐sponds to the two-facing-wall-driven square cavity flows with both walls moving at the same speed in the sameand oppositedirections.Notice however that the Reynolds number in the previous symmetric cases,as discussed in the literature,is usu‐ally defined asCom‐parison of results requires an appropriate correction to the advective time scaleand Reynolds num‐berRe=In the present study,we will focus on the case with the two walls moving in opposite directions,which corresponds to the octantα∈[−π/4,0](dark grey region shown in Fig.1b).
We choose to solve the 2D equations of motion inside the cavity with the 9-bit D2Q9 lattice Boltzmann model presented by Qian et al.(1992) and the nonequilibrium extrapolation scheme proposed by Guo et al.(2002),which provides second-order accuracy in both space and time.The numerical method has been coded in-house and extensively tested in the past (An et al.,2019,2020a,2020b),where thorough meshindependence studies were undertaken.Based on the previous experience and comprehensive mesh conver‐gence analysis,the square cavity has been resolved with a uniform Cartesian mesh ofNx×Ny=1024×1024 grid points in the horizontal and vertical directions,respectively.
For the sake of simplicity,simulations have been carried out with a top wall velocityUT=0.1,and as a result,the associated Mach number is given asM=according to the LBM particulars.The bottom wall velocity has been made to vary in the rangeUB∈[−0.4,0.0].Cases with |UB|>|UT| are redundant on account of the symmetries of the problem,but have been run all the same as a check for numerical com‐pressibility effects associated to LBM.All runs have however been mapped onto theα∈[−π/4,π/4] quad‐rant using the symmetries as required and consistently non-dimensionalised to allow straightforward com‐parison.The bulk Reynolds number is prescribed through the adjustment of the relaxation time parame‐terτvia the relationwhereis the particle velocity across the lattice.Four probes used to collect time series are planted inside the domain,and their coordinates are respectively given byP0=(0,0),PB=(0,−L/4),PT=and
Parameter space has been systematically explored by continuously increasing the bulk Reynolds numberRealong nine straight lines along tanα=−0.05,−0.10,−0.25,−0.50,−0.75,−0.95,−1.00,−2.00,and −4.00.The cases tanα=−2.0 and −4.0 correspond to symme‐try operations on the cases tanα=−0.50 and −0.25,re‐spectively,but with higher associated Mach numbers(M=-0.3464 andM=-0.6928 respectively for tanα=−2.0 and −4.0),so that differences in the results can be fully ascribed to compressibility results and serve therefore as a further validation of the method.
The critical Hopf has been re-computed for theα=−0.2449 and −0.4640 cases but with larger values of the dimensional velocities used in the LBM simula‐tions (these were in fact the cases with tanα=−2.0 and−4.0).The maximum lid velocity was therefore in‐creased from 0.1 to 0.4 and 0.2,respectively,evidently challenging the incompressibility limit.As point of fact,the case doubling the maximum dimensional lid ve‐locity pushed the Hopf bifurcation slightly fromReH=15930±60 to 16070±140 showing acceptably low compressibility effects.This was not so for the case multiplying the maximum velocity four-fold,which resulted in a considerable increase fromReH=13450±50 to 14220±200.It is therefore obvious that the im‐plementation of LBM used in this study is not appro‐priate when using lid velocities beyond 0.2.Keeping the lid velocity low,with its inconvenient impact on the time step,is mandatory.Or else,a variant of the LBM fulfilling incompressibility might also be used(Guo et al.,2000).
3 Results and discussion
The casesα=were thoroughly analyzed by An et al.(2020b),where the bifurcation path leading to the onset of chaotic dynamics was presented along‐side a detailed inspection of the evolution of the flow topology and its symmetries.Notice that for this par‐ticular case,in which the top and bottom lids are mov‐ing in opposite directions with the same speed,the asymmetry shows up as the instability appears.Here we extend the study to intervening negative values ofαin order to clarify the evolution from the cavity flow driven by two mutually facing walls sliding with equal but opposed velocities to the classic lid-driven cavity flow,represented byα=0.The aim remains the same,namely the identification of the transition path that leads to chaotic dynamics and the characteriza‐tion of the flow topology along the way.The computa‐tional cost of pinpointing the precise critical values of the parameters for each one of the bifurcations is unaf‐fordable with only a time-stepping code.We choose in‐stead to provide ranges for the transitions,which we express through a best estimate plus/minus a devia‐tion.The best estimate is obtained by averaging the parameter values of the threshold solutions before and after each bifurcation while the maximum deviation results from the parameter step between the same two bordering solutions.
3.1 Hopf bifurcation
Forα=the flow transition from steady to unsteady periodic arises as the top (and bottom) lid Reynolds numbers are increased simultaneously from 10100 to 10200 (An et al.,2020b).In terms of the bulk Reynolds number,the Hopf bifurcation occurs accordingly somewhere aroundReH=14390±25.Forα=0 (the classic lid-driven square cavity flow),the Hopf bifurcation is known to be supercritical and to occur forReH=8025±25 (Auteri et al.,2002;Bop‐pana and Gajjar,2010;Kalita and Gogoi,2016;Nu‐riev et al.,2016;An et al.,2020b).
Fig.2 shows the critical bulk Reynolds number for the Hopf bifurcation as a function ofα.The bifur‐cation has been determined to within about 50 Reyn‐olds number units.The bulk Reynolds number increas‐es fast from the classic lid-driven square cavity flow case as the second (facing) wall is set into opposing motion.As a matter of fact,the Hopf bifurcation is postponed toReH=16130±30,about double of the orig‐inal value (α=0),by the timeα=−0.464 is reached.But the stabilizing trend is thence reversed and the critical point for the onset of time-dependence is brought down to aboutReH=14390±25 forα=There is a relative minimum when the value ofαis larger than or approximately equal toBecause of the sym‐metries of the problem,the caseα=must act as a relative extremum,all properties having null slope as a function ofα.Therefore,the bulk Reynolds numbermust either be a relative minimum or,apparently in this case,a relative maximum.The fre‐quencyfof the first periodic solution encountered up‐on increasing the bulk Reynolds number at a fixedαhas been used as a harbinger of the Hopf frequencyfH.These are shown in Fig.2.Starting from the clas‐sic lid-driven cavity flowα=0,withf=0.4425 (Auteri et al.,2002;Boppana and Gajjar,2010;Kalita and Gogoi,2016;Nuriev et al.,2016;An et al.,2020b),the Hopf frequencyfHinitially declines asαis reduced into negative values.The decrease is only mild and reachesf=0.425 forα=−0.099 before bouncing back.From this point,the frequency rapidly increases to fi‐nally reach a maximum of aboutf=1.222 forα=It is realized as well,the 3D instabilities are supposed to occur far beforeRe=10000,if a cuboidal lid-driven cavity with square cross section is considered (Romanò et al.,2017,2020).
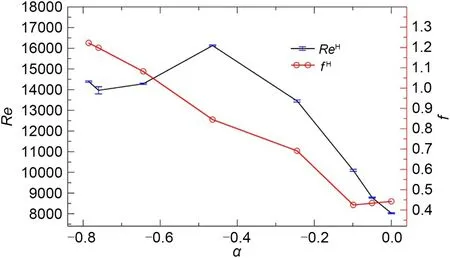
Fig.2 Hopf bifurcation in Re-α parameter space.The critical Reynolds number for the Hopf bifurcation (ReH) is shown as a function of α (black line,blue error bars denote uncertainty in its determination) along with the Hopf frequency (f H),as approximated by the frequency of the first periodic solution after crossing the Hopf point.References to color refer to the online version of this figure
Fig.3 compares various steady state solutions for differentαin the immediate vicinity of the Hopf bifurcation.As expected,there is a large central vor‐tex flanked by three smaller vortices forα=0 (Fig.3a).Reducingαnoticeably changes the bottom-right cor‐ner vortex (Fig.3b).Further decreasing toα=−0.2449,the flow in this bottom right corner develops into a πrotated weaker version of the vortical structure at the top-left corner,while the vortex in the bottom-left cor‐ner clearly weakens (Fig.3c).Beyond this point,the π-rotational symmetry is gradually but steadily restored and then fully recovered whenα=is reached(Fig.3d).
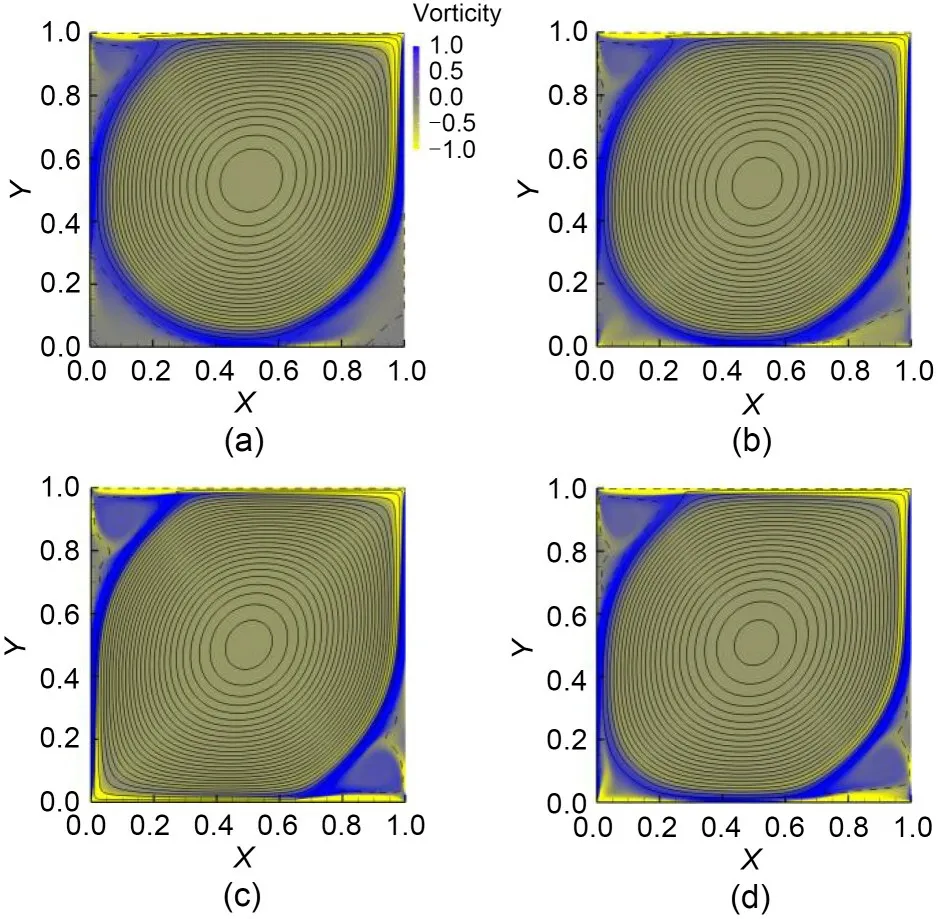
Fig.3 Stream function isolines and vorticity color maps of steady solutions at Reynolds numbers just before the Hopf bifurcation.Vorticity ranges from −1.0 (yellow) to+1.0 (blue),as indicated by the color bar panel: (a) Re=8000,α=0;(b) Re=10050,α=−0.099;(c) Re=13400,α=−0.2499;(d) Re=14354,α=−π/4=−0.7854.References to color refer to the online version of this figure
Beyond the Hopf bifurcation the flow becomes periodic,as illustrated forα=-0.644 atRe=14313 by the time signal,phase map,and spectrum of Fig.4.The main panel depicts the Fourier transformation of the horizontal velocityuxat pointPTR,and the time signal is shown in the top inset.The spectrum has a sharp peak atf=1.082 (associated period0.9242) and secondary (harmonic) peaks at integer multiples,as corresponds to a periodic signal.Fig.4b shows the phase trajectory of a periodic solution,being a closed loop.

Fig.4 Periodic solution for α=−0.644 at a bulk Reynolds number Re=14313: (a) spectral power density || of the horizontal velocity signal ux as measured at probe PTR;(b) phase-map projection on the ux-uy plane.uy is the vertical velocity
As previously stated,the following vortex color maps are sketched without showing the cavity axes for a better view of the flow topology details along the edge.For the classic single-lid-driven cavity (α=0,Fig.5a),the time dependence shows mainly as a wave train of vorticity knots that travels clockwise along the outward perimeter of the central core vortex.The top-left corner vortex shrinks and grows as the passage of the wave compresses and releases the space it occupies.This oscillation in size of the top-left corner is also largely perceptible forα=-0.099 (Fig.5b),but the wavy oscillation of the core vortex boundary is no longer as conspicuous.The situation remains fairly unaltered forα=-0.2499 (Fig.5c) as the new vortex at the bottom-right corner,which has grown discern‐ible already for the steady solution,appears quite un‐affected by the dynamics,possibly due to the lower local Reynolds number associated with the bottom lid.As the symmetry parameter increases towardsα=−π/4,the flow gradually evolves into a space-time symmetry consisting of invariance to evolution by half a period followed by π-rotation.This symmetry is ev‐ident atα=−π/4 (Fig.5d),where any two snapshots exactlyapart are related by a π-rotation.For a better grasp of the time-dynamics,Videos S1–S5 at the same values of the driving parameters are provided in the ESM.

Fig.5 Vorticity color maps of periodic solutions.Four snapshots are shown at instants 0,T/4,T/2,and 3T/4 equispaced along a full period T and the corresponding values of the parameters are: (a) Re=12000,α=0;(b) Re=10351,α=−0.099;(c) Re=14431,α=−0.2499;(d) Re=14496,α=−π/4.Cavity size and color coding as for Fig.3 (Videos S2–S5 in the ESM)
3.2 Quasi-periodic and chaotic onset
A sufficient further increase of the bulk Reynolds number at a fixedαdestabilizes the periodic solution and the flow evolves into quasi-periodicity.Taking the case (α=-0.644) for illustration purposes,the flow is found to remain periodic up toRe=15438,well beyond the Hopf bifurcation,but it becomes quasi-periodic instead forRe>15625,which points at the advent of a Neimark-Sacker bifurcation.Beyond this bifurcation,the flow is observed to finally evolve into chaos,fol‐lowing a prototypical Ruelle &Takens scenario (Ruelle and Takens,1971;Newhouse et al.,1978).Fig.6a shows phase-map trajectories as well as the frequency spectrum atRe=15438 and 15625 forα=-0.644.While the former closes in a loop every period,the latter possesses,beyond the fast dynamics that are evidently associated to the former solution,a second slower timedynamics that makes the trajectory wind around a torus,filling it densely.AtRe=15438,the spectrum in Fig.6b confirms the periodic orbit hypothesis,with an associated non-dimensional frequencyf1=1.05.Notice that all other peaks are mere harmonics of the funda‐mental frequency.The sable periodic orbit is replaced,atRe=15625,by a quasi-periodic solution.The spec‐trum remains discrete but peaks arise at all linear com‐binations of the fundamental (ostensibly inherited from the periodic solution)f1=1.049 and modulationalf2=0.119 frequency peaks.The rotation number isf1/f2=8.815,which explains why the phase-map trajectory almost closes every pseudo-periodic loops.
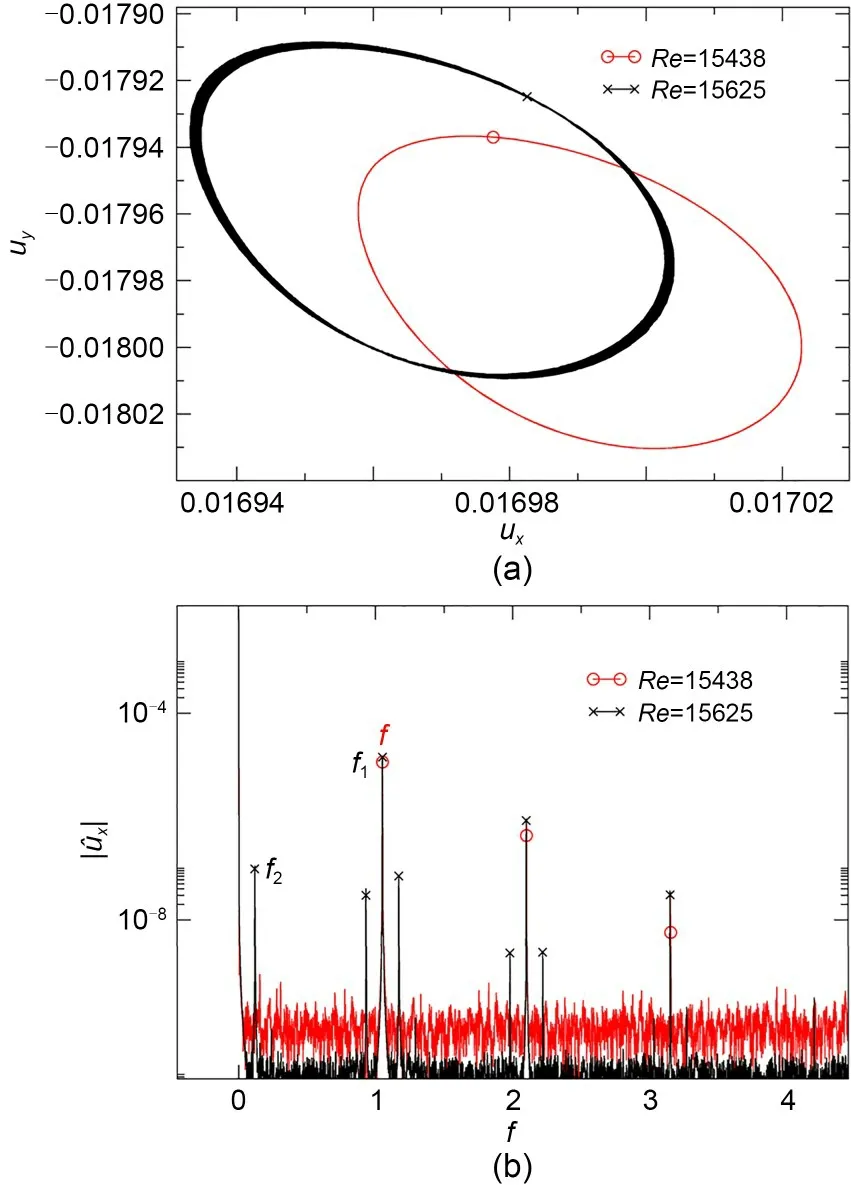
Fig.6 Neimark-Sacker bifurcation for α=−0.644: (a) phasemap trajectories projected on the ux-uy plane as measured by probe PTR of periodic (red,Re=15438) and quasi-periodic(black,Re=15625) solutions just before and after bifurcation;(b) spectrum of the horizontal velocity signal ux from the same probe and for the same solutions α=−0.644.References to color refer to the online version of this figure
The modulational frequency peak is distinct though barely noticeable,but quasi-periodicity devel‐ops non-linearly as the bulk Reynolds number is further increased beyond the Neimark-Sacker bifurcation,which we pinpoint atReNS=15470±30.
Moving to slightly larger values ofRe>15750,Fig.7b depicts theuxspectrum across the transition from quasi-periodicity into chaos.The flow inside the cavity is undoubtedly quasi-periodic atRe=15750,but becomes gradually chaotic as the bulk Reynolds num‐ber is increased to 15875 and beyond.While,the spec‐trum still shows some remnants of the original fre‐quenciesf1andf2,the fundamental peaks are now sur‐rounded by broadband noise associated to chaotic dy‐namics Reynolds numbers.
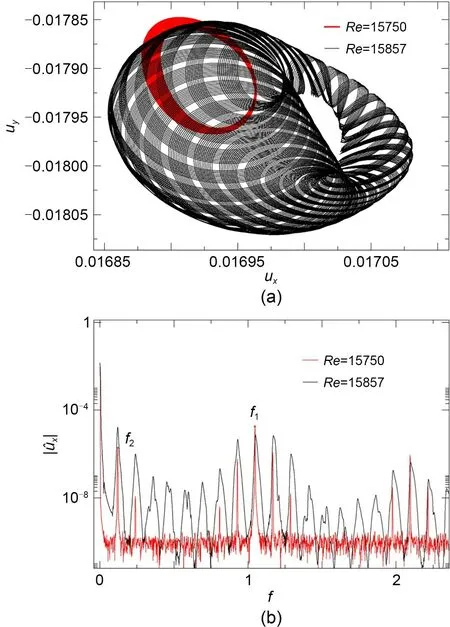
Fig.7 Onset of chaotic dynamics for α=−0.644: (a) phasemap trajectories projected on the ux-uy plane as measured by probe PTR of quasi-periodic (red,Re=15750) and time-chaotic(black,Re=15875) solutions just before and after the global bifurcation;(b) spectrum of the horizontal velocity signal ux from the same probe and for the same solutions.References to color refer to the online version of this figure
The slow time-dynamics associated to quasiperiodicity is barely detectable in any representation of the flow fields,its effect merely consisting in a very slight modulation of the fast dynamics already de‐scribed for the periodic solutions.A Poincaré sectionhas been purposely defined in order to quotient out the fast dynamics associated to the Hopf frequency.Subsequently,the effects of the modulational frequency on the flow field can be illustrated through a collection of snapshots from these crossings.In particular,three consecutive crossings of the Poincaré section are sufficient for the solution to complete a full revolution on the torus surface,as required by the specific value the rotation num‐ber takes.The corresponding vorticity color maps are shown in Fig.8.Videos S6–S10 are provided for various values ofαin the ESM to show how the fast dynamics completely masks the manifestation of the slow dynamics.

Fig.8 Quasi-periodic solution for various values of α as illustrated by vorticity color maps of snapshots taken at three consecutive crossings (n0 is the first crossing) of a Poincaré section defined by ux=and ∂ux/∂t>0 as required by the rotation number for a full winding around the torus:(a) α=0, Re=14000;(b) α=−0.099,Re=11557;(c) α=−0.464,Re=17888;(d) α=−0.760, Re=15862;(e) α=−π/4, Re=19799.Cavity size and color coding as for Fig.3 (Videos S6–S10 in the ESM)
The differences upon successive crossings evince the modulational dynamics of the quasi-periodic solutions emerged from the Neimark-Sacker bifurca‐tion.Due to the proximity between the Neimark-Sacker and the onset of chaos,the casesα=−0.099(Fig.8b) and −0.760 (Fig.8d) barely show any indi‐cation of quasi-periodicity,although close inspection does indeed reveal some modulational dynamics (the related videos in the ESM).The stroboscopic effect is instead very prominent for the classic cavity (Fig.8a),with the vorticity knots that circle the core vortex evi‐dently pulsate at every consecutive crossing of the Poincaré section.The same effect is apparent on the top-left and bottom-right vortices forα=−0.464 (Fig.8c)and sticks particularly out for the symmetric caseα=−π/4 (Fig.8e),as the quasi-periodic solution has been able to evolve non-linearly far from its bifurcation point thanks to the strong resistance of the flow to the final destabilization into chaotic motion (Videos S11 and S12 in the ESM).
The Neimark-Sacker and chaotic-transition points have been extended into lines by carrying the analysis just illustrated to all other values ofαconsidered.The dependences onαof the critical values associated to the Neimark-Sacker (ReNS) and the global bifurcation (ReC)that triggers chaotic dynamics are presented in Fig.9,alongside those corresponding to the preceding Hopf bifurcation (ReH).Both critical values start high for the classic lid-driven square cavity and drop sharply as the bottom wall is set in anti-parallel motion.Minimum critical valuesReNS=10110±50 andReC=10930±130 are observed forα=−0.0499 and −0.0990,respectively.The trend is reversed at the minimum,and the critical values grow fast to reach a plateau around a maxi‐mum that,in our coarsely discretized parameter space,we identify atα=−0.499.The maximum is global for the Neimark-Sacker,withReNS=16490±50,but only local for the transition to chaos,withReC=20000±150.Reducingαbeyond -0.0464 bringsReNSslowly down to a new minimumReNS=15340±170 forα=-0.760,before bouncing towards a final maximumReNS=15630±70 atα=−π/4.Something similar happens for the onset of chaos,expect that the drop from the maximum atα=−0.499 is somewhat sharper,that the minimum atα=−0.760 isReC=15690±130,and the maximum forα=is global atReC=23690±350.It therefore seems that a very slight asymmetry in the driving velocities destabilizes the flow into chaotic dynamics much more efficiently than the increase of the bulk Reynolds number.
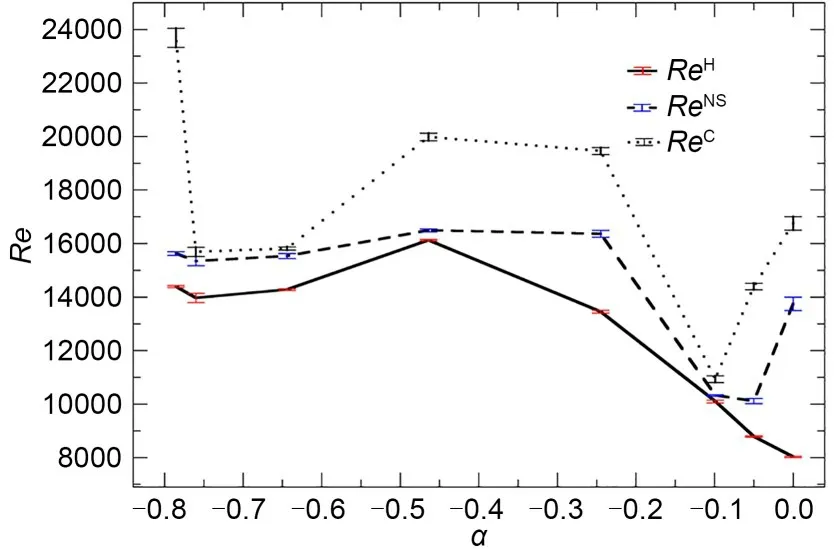
Fig.9 Critical value for the Hopf (ReH,solid line),Neimark-Sacker (ReNS,dashed),and chaos-triggering (ReC,dotted)bifurcations in Re-α parameter space.Error bars indicate the degrees of uncertainty in the determination of the critical lines
Fig.10 depicts the chaotic solution at Reynolds numberRe=19375 andα=-0.644.The flow topology of the solution is illustrated by a single instantaneous snapshot of stream function isocontours and vorticity color map in Fig.10a.The large central vortex still dominates the bulk of the flow and the overall flow to‐pology is not very different from the steady solution at somewhat lower values ofRe.The solution is tem‐porally chaotic but not spatio-temporally chaotic,at least when assessed globally.The small eddies at the top-left and bottom-right corners,however,become decorrelated from one another,as comparison with the periodic solution at a different value ofα(α=−π/4 andRe=14496,Fig.5d),reveals.The vorticity color map underlines the regions where high shear is to be found.The interfaces between the main core vortex and the smaller corner vortices are responsible for the instability that introduces chaotic dynamics.The solu‐tion is temporally chaotic,as clear from the phase-map projections of Fig.10b.Fig.10c presents the spectrum of theuxvelocity signal (shown in the inset).Besides the broadband noise that pervades the full spectrum,the fundamentalf1and modulationalf2frequencies in‐herited from the quasi-periodic solution are still clearly recognizable,indicating that the solution retains a large degree of coherence.
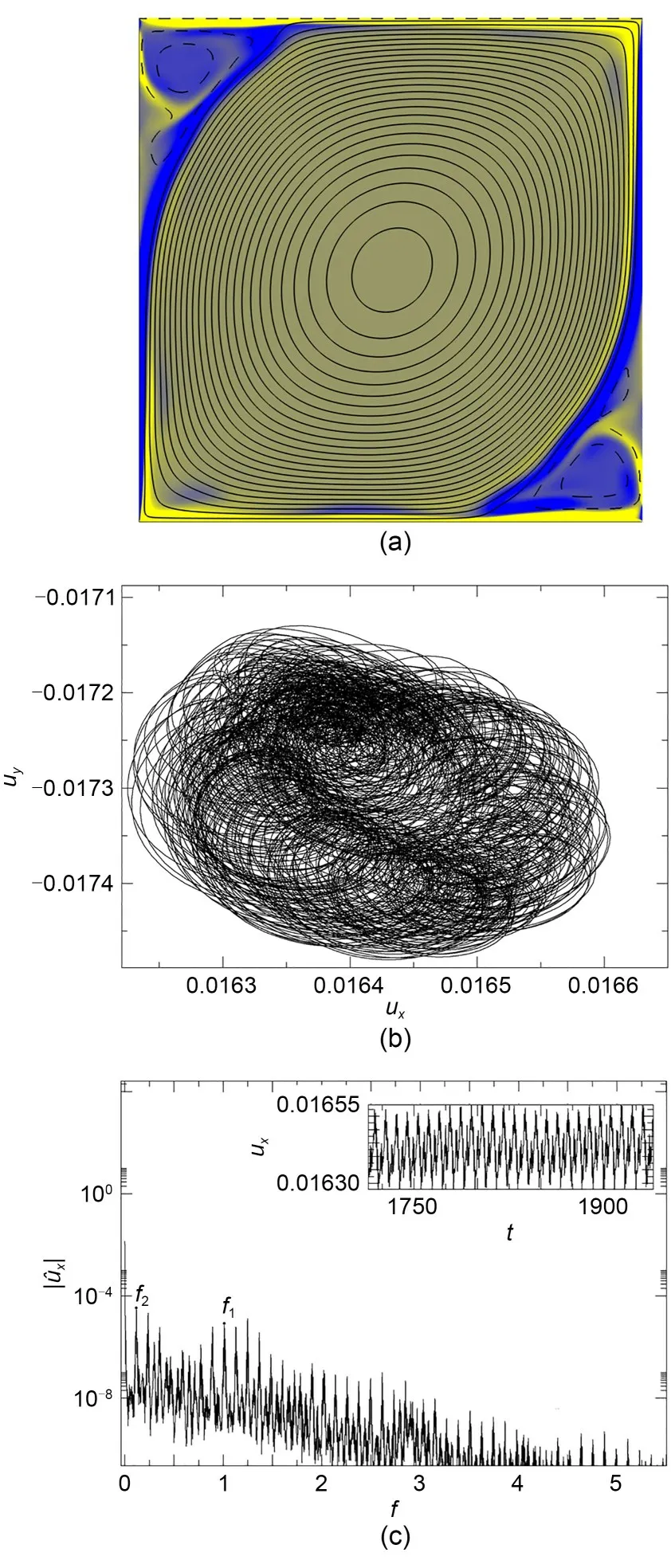
Fig.10 Chaotic results at Re=19375,with α=−0.644:(a) stream function contours and vorticity color map (cavity size and color coding as for Fig.3);(b) phase-map projection on the ux-uy plane;(c) spectrum || of time series ux (inset)
In Fig.11,the two relevant frequency peaks la‐belled asf1andf2are again observed in logarithmic scale.The frequencyf1,characterizes the higher energy level associated to the time dynamics of the main cen‐tral vortex in Fig.10a.The frequencyf2represents instead the small-scale vortex interaction dynamics.Around this particular peak,several similar peaks also arise.We speculate that these peaks are characterizing the smaller vortical structures also appearing nearby the two vortices at the top-left and bottom-right cor‐ners.Notice that in the inertial subrange,the energy decays with a slope very close to −5/3,in good agree‐ment with published data (Jiménez,2012;Vassilicos,2015;Alexakis and Biferale,2018).Videos S11 and S12 show the flow dynamics of theα=-0.644,Re=19375 and 23750 cases.
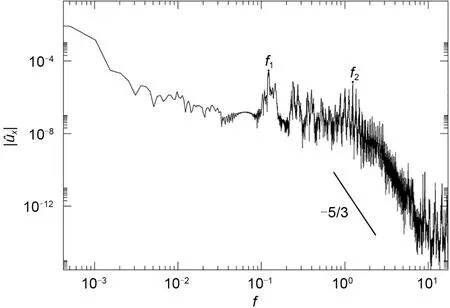
Fig.11 Spectral decomposition of time series ux at Re=19375,with α=−0.644
4 Conclusions
We have explored the effects of the independent sliding of two mutually facing driving walls on the flow within a square cavity.The two degrees of free‐dom associated with the two independent wall veloci‐ties have been parameterized using a bulk flow param‐eter,the bulk Reynolds numberRe,and an asymmetry parameterαfor the driving velocities.In this setting,α=0 represents the classic lid-driven cavity flow,whereasα=−π/4 corresponds to the two facing walls moving in opposite directions at the same speed.All bifurcations,Hopf,Neimark-Sacker,and the onset of chaos,have been presented as a function of the param‐eterα,fully clarifying the transitional flow topology within two-sided square cavities.
We have found,as expected,that the first insta‐bility is always a Hopf bifurcation,such that the flow becomes periodic.The classic lid-driven cavity is the one that destabilizes earliest,the motion of the second lid having a stabilizing effect.The stabilization is maxi‐mal forα=−0.464,with smaller (negative) values tend‐ing to reduce the critical valueReH.The caseα=−π/4,however,is a relative maximum forReH,meaning that the desymmetrisation from equal speeds has locally a slightly stabilizing effect.
The destabilization of the periodic solution oc‐curs,for the values of the parameters prescribed here,always through a Neimark-Sacker bifurcation.The trend of the critical curve is however different from that cor‐responding to the Hopf bifurcation.Setting the second lid in motion has a highly destabilizing effect for the periodic solution.Therefore,the periodic solutions are confined to a very narrow range ofReforα=−0.1.A similar effect takes place forα=−0.464 despite periodic solutions being stabilized,on account of the steady so‐lution being strongly stabilized (Fig.9).
Quasi-periodic solutions seem to break into cha‐otic dynamics for allαexplored.Forα=−0.1 and close to −π/4,quasi-periodicity subsists within a rather nar‐row range of Reynolds numbers.At exactly −π/4,however,the quasi-periodic solution is strongly stabi‐lized.It seems that the π-rotational symmetry has the effect of delaying chaos to a large extent.
Acknowledgments
This work is supported by the projects of the North‐western Polytechnical University (No.G2021KY05103),the Natioanl Key Laboratory of Science and Technology on Aero‐dynamic Design and Research (No.614220121030101),the Key Laboratory of Icing and Anti/De-icing of China Aerodynamics Research and Development Center (No.IADL20210302),the Spanish Government (Nos.FIS 2016-77849-R and PID2020-114043GB-I00),the Catalan Government (No.2017-2017-SGR-00785),and the Barcelona Supercomputing Centre (Nos.FI-2017-2-002,FI-2017-3-0009,and FI-2016-3-0038).
Author contributions
Bo AN took in charge of the code writing,validation,and modifications.Bo AN,Weimin SANG,and Dong LI evaluated the simulation performance and prepared figures.Bo AN,Wei‐min SANG,Josep M.BERGADÀ,and F.MELLIBOVSKY wrote the main manuscript text.Weimin SANG,Dong LI,Josep M.BERGADÀ,and F.MELLIBOVSKY reviewed the manuscript and suggested for manuscript modifications.F.MELLIBOVSKY took the whole in charge of the present study.
Conflict of interest
Bo AN,Josep M.BERGADÀ,Weimin SANG,Dong LI,and F.MELLIBOVSKY declare that they have no conflict of interest.
杂志排行
Journal of Zhejiang University-Science A(Applied Physics & Engineering)的其它文章
- Numerical investigation of the effect of geosynthetic clay liner chemical incompatibility on flow and contaminant transport through a defective composite liner
- Monotonic uplift behavior of anchored pier foundations in soil overlying rock
- Fractal analysis of small-micro pores and estimation of permeability of loess using mercury intrusion porosimetry
- Underwater minirobots actuated by hybrid driving method
- Bogie active stability simulation and scale rig test based on frame lateral vibration control
- Analytical solution of ground-borne vibration due to a spatially periodic harmonic moving load in a tunnel embedded in layered soil
