数学中考复习减负提效探索
2023-07-23朱菊香
朱菊香


摘要:中考复习中落实“双减”既要减轻学生的心理压力又要减轻课业负担,这就需要提高复习效率.教师可立足教材,精选书本例题,进行变式训练,举一反三;也可发挥中考试题功能,选择中考典型题,让学生掌握考查的深度与广度,明确复习重点;亦可精心设计习题,促进知识内化,省时高效地达到训练目的.
关键词:“双减”;中考;复习;提效
中考数学复习有助于学生巩固知识、加深理解,提高综合运用知识的能力,是一项特殊的教学活动.但是在传统观念“熟能生巧”的影响下,总复习阶段超量的练习.不仅严重地增加了学生过重的课业负担.而且使学生大脑活动由兴奋转向抑制,高劳低效,事倍功半,也不利于各学科间的协调复习.根据数学课程标准要求,数学课程应致力于实现义务教育阶段的培养目标,要面向全体学生,适应学生个性发展的需要,使得:人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.现就结合自身的教学实践和教研经验,就中考复习过程中如何减轻学生过重课业负担,谈一些体会.
1落实“双减”减轻学生心理压力
“减负”作为一项复杂的社会系统工程,要使此项工作取得显著成效,首先要减轻学生的心理压力.必须为学生创设一个相对宽松、和谐的成长环境,使学生拥有良好的心境.到了复习阶段,一个学生的成绩好坏,基本能显现出来了,数学学科尤其明显.要求教师不能搞整齐划一,以一个标准要求全班学生,应该建立学生的个人档案,熟悉每个学生的情况,并针对学生的不同情况提出不同要求,體现在复习过程中,就是分层施教,分类布置练习,使每一个学生经过努力都能有所发展.其次更应注重教给学生学习方法,激发其学习主动性.使学生具有获取知识、发展个性特长的机会和空间.三是注重学生非智力因素的培养,加强学生心理健康教育.到了复习阶段,由于应试教育作怪,有的学生因教师排名公布往往会自暴自弃,因此,教师应勤于观察,善于分析,认真研究造成学生不良心理状态的原因,及时加以疏导,从而促进学生身心健康发展.
2发挥中考试题功能彰显书本知识要点
中考试题是命题者依纲据本,以课本例、习题为“背景”经过巧构妙思设计的典型题,不仅在一定程度上浓缩了课本重要的基础知识和基本技能,而且蕴涵着丰富的数学思想和思维方法.有的放矢地择取中考试题,融于知识的系统复习与方法的巩固之中.特别对领悟复习重点,是选用中考试题的首要目的.在每一章节复习时,通过展示与剖析相关的试题,可使学生深刻认识该章节应掌握的重点内容以及中考考查的深度与广度,明确方向,避免走弯路,这是课本、复习资料上的题目所不可替代的.
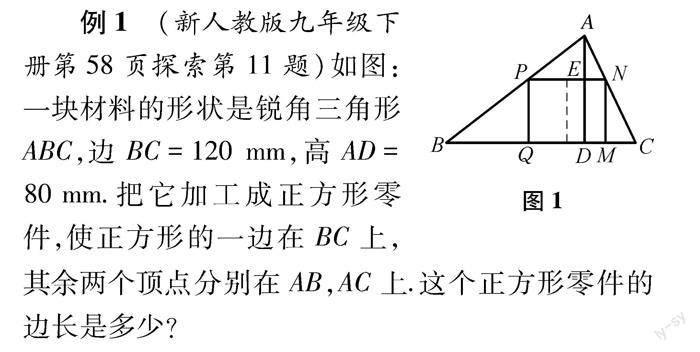
例1(新人教版九年级下册第58页探索第11题)如图:一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm.把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.这个正方形零件的边长是多少?
分析:利用相似三角形的高之比为相似比.预测分析试题的变化:①从外部看,锐角三角形ABC;②从内部看,正方形;③内部特殊线段:高线.
例2(2014年浙江绍兴中考)
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
考点:相似三角形的应用;二次函数的最值.
分析:(1)根据相似三角形对应高的比等于相似比,列出比例式求出即可;
(2)根据相似三角形对应高的比等于相似比,列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答.
另外,在总复习教学中,以课本习题中考试题为题源,运用不同的知识和手段,变换题目的形式和背景,整合出综合自然、新颖脱俗的试题,对于提高学生的认识层次、强化探索能力,摒弃题海战术,是行之有效的途径.
3精挑细选例题变式发散训练
例题讲解力求“变化”.复习课的例题应选择最有代表性,能突出教材重点、反映大纲基本要求的题目,注重发挥例题以点带面的功能,并且有意识地对例题进行变化,挖掘问题的内涵和外延,提高思维的深度与广度,培养学生随问题变化而变化的应变能力,力争“讲一题、学一法、会一类、通一片”.变化的基本方法有:(1)变化解题法,训练发散思维;(2)对例、习题进行变化,作出类比、推广或引申;(3)题型变化,封闭性变化为开放性、证明计算题;(4)变问题情境、变图形位置、变数、变符号,这样通过变式训练,不仅有利于学生更加直接触及数学问题的实质,沟通知识间的内在联系,还对学生的观察分析能力,形成准确的解题技巧大有裨益,起到举一反三的作用,事半功倍的效果.
例1(新人教版八年级上册第44页综合运用第9题)如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
评析:本题主要训练学生运用“边边边”条件BECF判定三角形全等,进而运用全等三角形的性质得出所求证的角相等.由条件BE=CF不难得出BC=EF,又有已知条件AB=DE,AC=DF.利用“边边边”条件可得△ABC≌△DEF,从而∠A=∠D.就是这样的一道习题,却成了近几年多省市中考命题的源泉,正所谓中考题是“源于课本又高于课本”的变式题.
(1)保持原图不变,变换已知条件和结论
例2(2022年淮安中考)已知:如图,点A、D、C、F在一条直线上,且AD=CF,AB=DE,∠BAC=∠EDF.求证:∠B=∠E.
评析:将原题条件和结论变化得本题,从另一个角度考查三角形全等的“边角边”判定.由AD=CF可得AC=DF,又有∠BAC=∠EDF,AB=DE,所以△ABC≌△DEF.
例3(2020年常州中考)已知:如图,点A、B、C、D在一条直线上,EA∥FB,EA=FB,AB=CD.
(1)求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
评析:利用原题图,变化部分条件和结论得考题,考查学生对三角形全等的条件及全等三角形的性质的掌握情况,判定条件为“边角边”.
(2)保持原图不变,探索问题
例4(2011年福建南安中考)如图,已知点E、C在线段BF上,BE=CF,请在下列四个等式中,①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出△ABC≌△DEF,并予以证明(写出一种即可).
已知:______,______.求证:△ABC≌△DEF.
評析:以原图为载体,借助所给的多个条件探索三角形全等,颇具开放性.考查学生对三角形全等的条件的掌握情况和探索能力.
例5(2010年四川泸州中考)如图,已知AC∥DF,且BE=CF.
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是______;
JP3评析:以原图为载体,在已有条件的基础上补充一个条件并证明三角形全等,具有一定的探索性、开放性.
(3)适当变化图形,考查同类内容
例6(2018湖北武汉中考)如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
评析:对原题图形作适当变化,仍然考查三角形全等,可谓形变质不变,解题思路不变.
例7(2021年江苏无锡中考)已知:如图,AC、DB相交于点O,AB=DC,∠ABO=∠DCO.
求证:(1)△ABO≌△DCO;
(2)∠OBC=∠OCB.
评析:对原题图形作适当变化,既考查了全等三角形判定与性质,同时又考查了等腰三角形的性质,是一题很好的综合解答题.
(4)变化部分图形位置,考查同类内容
例8(2022年江苏南通中考)如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,只需添加一个条件,则这个条件可以是______.
评析:将原图中的一个三角形翻折使A、D两点位于BE两侧而得本题图,考查的内容仍是三角形全等的有关内容.
(5)变化部分图形位置,探索问题我们只有立足教材,充分发挥课本例题、习题的功能,重视课本中典型例题、习题的演变、延伸和拓广,对例题、习题进行一题多解和一题多变的变式训练,引导学生利用已有的知识与经验,主动探索知识发生和发展的过程,增强学生的应变能力,有利于巩固基础知识,发展创新思维,提高数学素养,更利于提高学生的数学成绩.
4跳出题海战役精心设计习题
在数学复习过程中,需要教师精心设计习题,教师要跳进“题海”,亲自把习题做一遍.从而了解哪些基本题,哪些难度较大,哪些综合性较强,哪些属于一题多解,哪些题应该布置给哪一个层次的学生,哪些题什么时候布置,要认真琢磨,真正提高习题的质量,才能省时高效地达到训练目的,而不至于使学生陷入“题海”不能自拔,无端增加学生负担.
(1)改“盲目型”为“针对性”,促知识内化.这样有利于学生集中力量突破难点,掌握解题思路.
(2)改“再现型”为“建构型”,促知识建构.培养技能技巧,并能以题及类,以点带面,以少胜多.复习练习设计,应当有别于新授课.它不能完全是知识的巩固,而要在复习的过程中加深其对所学知识的理解.还要加强知识之间的前后左右的联系,促使学生知识网络的形成.
(3)改“统一型”为“差异型”,促思维发展.复习练习,设计的习题要有层次性,教师注意安排一定的提高题,帮助学生深化知识,发展思维.但是提高题也要照顾到“好、中、差”三类学生,分为A、B、C三组,A组题以模仿为主;B组题以熟练掌握为主;C组题以灵活运用为主,题目综合性较强,涉及知识面较宽,解题的方法具有一定技巧.使学生既可以接受,又学有兴趣,促进基础知识的牢固掌握.
总之,“减负提效”势在必行,这实际上是给教师提出了一个更高的要求.强化自身素质,提高业务水平,努力让教学更加科学、适度、生动、高效,这是每一位教师努力的目标.
