核心素养视角下单元复习课的探索与思考

吴婧婧 查晓东

摘要：单元复习课既是一个单元的结束，也是另一单元的开始，因而教学设计需要充分地体现在大单元中的整体性与连续性，应该从“梳理知识结构、渗透研究方法、落实核心素养”三个层面展开，实现学生对章节内容的深度思考、深度探究，从而达到深度理解.本文结合一节单元复习公开课的教学设计，呈现核心素养视角下对单元复习课的若干思考.

关键词：单元复习；大单元；深度学习；核心素养

单元复习课是数学教学中不可或缺的一种课型，它不仅仅是知识点的简单罗列，各种题型、方法的归纳总结，更有别于高三专题复习课，应该从整体上把握知识的发生发展过程，着眼于建构本章的知识结构与研究方法.本文通过笔者开设的《直线与方程》这一单元复习课，谈一谈核心素养视角下单元复习课的有效设计与开展.

1教材分析

直线与方程这一章节是学生学习解析几何的第一次体验，在整个解析几何体系中具有思想方法的引领作用，这就要求教师要在教学过程中充分渗透解析几何研究问题的一般方法，帮助学生建构后面学习过程中所需要的知识和研究路径，通过深度学习充分落实学生数学抽象、逻辑推理、数学建模、数学运算、直观想象等核心素养.

本节课所使用的教材是苏教版普通高中教科书数学选择性必修1，教学时以知识的展开和研究的路径为明线，以坐标思想的贯穿为暗线，在知识的学习中建构研究方法，在方法的建构中渗透思想，在思想的渗透中提升核心素养.

2过程设计

2.1回顾研究过程，构建研究框架

问题1：建立直线方程的过程是怎样的？

教师带着学生一起回顾直线方程建立的过程和关键，通过方程生成过程的回顾，再次理解直线方程的概念，体会几何问题代数化的过程，感悟直线斜率概念的重要性.在此环节的进行中可以发现学生对方程建立过程的理解是不够熟悉与深入的.通过对“斜率”概念抽象过程的复习回顾，让其内化概念本质的同时，也是对数学抽象和数学建模核心素养的再次渗透.

问题2：利用直线方程研究直线性质的方式是什么？

通过引导学生观看书上的目录，使其认识到利用方程所获得的性质，感受到坐标法的价值所在，同时稍作回顾梳理，让学生熟悉性质的研究内容，感受数形结合的思想.在之前的学习过程中，如果我们交给学生的知识是一颗颗珍珠，那么这个过程正是教会学生用线将其串成了一条项链，认识到其价值，而这根线就是思想方法，串项链的过程就是核心素养的培养.

问题3：归纳概括平面解析几何中研究直线的方式.

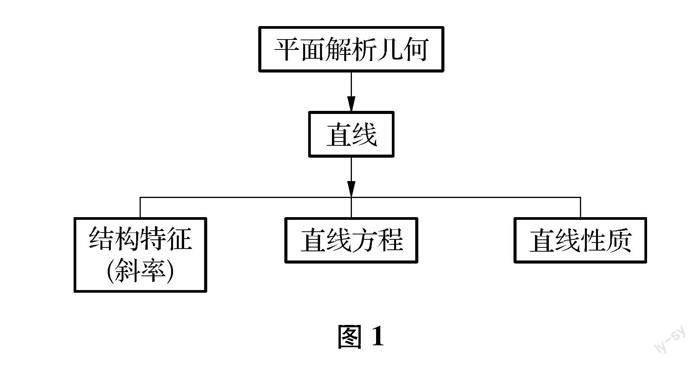
从以上直线到直线方程再到直线性质的研究回顾，归纳得到了平面解析几何中研究直线的方式（如图1），并且体会到解析几何中研究问题的一般方法（如图2）.这一具体到抽象的思维过程完成了知识复习的同时也将解析几何的思想和研究方法再次地得以具体化呈现，通过特殊到一般，具体到抽象的方式渗透研究问题的一般方法，促进学生高阶思维的发展，潜移默化中渗透逻辑推理和数学抽象核心素养.

2.2应用研究知识，提出并解决问题

探究1：已知△ABC的三个顶点A（0，4），B（3，0），C（6，6）你可以提出哪些问题？

学生提出了可以求解直线的方程，如：边、高线、中线等所在的直线方程；可以求解点的坐标，如垂足，中点，重心等一些点，在此过程中可以帮助学生完成方程五种形式的归纳整理，并注重方程形式的合理选择.

作为知识复习的补充，提出如下两个问题：

（1）判断直线l：x+3y+4=0与直线BC是否相交，若相交，求出交点坐标；

（2）若D（2，8），判断四边形ABCD的形状并求出四边形ABCD的面积.

通过这两个问题，对于直线的性质，主要是两直线的位置关系和距离加以复习，完善了学生的知识结构，同时也是对于解析几何思想的体会及运用，感受用代数方法解决几何问题的魅力.

探究2：证明三角形的三条高所在的直线交于一点.

证明：△ABC中，不妨设∠A，∠B为锐角，以AB所在直线为x轴，AB边上的高所在直线为y轴，如图3建系.设BC，AC边上的高分别为AD，BE，即证AD与BE的交点在y轴上.

AD：y=（b c）（x-a），BE：y=（a c）（x-b）.由 y=（b c）（x-a）

y=（a c）（x-b） x=0.即为所证.

探究2的解决既是知识的应用，更是解析几何思想的應用.从坐标系的建立到方程形式的选用再到几何问题向代数问题的转化，每一个过程既是知识的熟练应用，也是思想方法的深入体会，提升学生分析问题，解决问题的能力，让学生初步感受到代数问题与几何问题相统一的价值，在此过程中又一次地聚焦了学生的数学建模，逻辑推理，数学抽象，数学运算等核心素养.

2.3总结研究感悟，建构一般方法

在前面的回顾整理和知识应用中学生有了解析几何中对于直线研究的方法和知识储备，并且在情感上有了成功体验，能力上相应的核心素养也得以提升，此时此刻将直线的研究推广到一般的曲线研究就显得理所当然而又迫切需要，因而通过和学生的共同类比推广，得到了如下研究一般曲线的方法（如图4）.

3设计意图

单元复习课既是一个单元的结束，也是另一单元的开始，因而要充分地体现其在大单元中的整体性与连续性.直线与方程和后面的圆与方程，圆锥曲线与方程在知识与方法上都是一个大单元，在复习课的教学设计中要充分体现这一章节在这个大单元中的整体性、层次性和创造性.［1］

3.1以思想方法的渗透为主题

本节课的复习过程中，无论是问题的设计，探究活动的展开都是围绕着解析几何一般方法的渗透：将几何问题转化为代数问题，用代数方法解决几何问题.在解析法的引领下，让学生串联知识要点，理解研究过程， 应用知识解决问题，使得学生从大概念认识这一章节的内容，体会解析法的思想.

3.2以大框架，大思路的建立为主线

本单元的研究过程和后面的圆与圆锥曲线研究学习是一致的，因此在复习过程中应充分引导学生理解本单元的研究过程，自主建立研究曲线的大框架、大思路.直线这一章节的知识是最简单的，但是背后的思想方法是最难理解的，比如斜率的概念是如何产生的，这是从无到有的过程，是从直线方向中抽象出来的一个概念，因而如果能够充分理解这一章节，那么对于后面内容的理解也就顺理成章了.

4教学启示

4.1以聚焦核心素养为目标，促进深度学习

郭华教授提出，学生在深度学习的过程中，能掌握学科的核心知识，理解学科的学习过程，把握学科的本质及思想方法，形成积极的态度，正确的价值观，成为既具独立性、批判性、创造性，又有合作精神的未来社会的主人.［2］由此，数学深度学习有助于培养数学核心素养——具有数学基本特征、适应个人终身发展与社会发展需要的思维品质与关键能力.

一个单元的内容承载着相应数学核心素养的渗透，教师在单元复习课中应该聚焦这些核心素养，以其再次渗透和落实为目标，通过深度教学实现学生对这一章节深度学习：通过层层问题的引领，让学生在问题解决中体验知识之间的关联，掌握数学的核心知识，理解学习的过程，把握这一章节的本质及思想方法，形成积极的内在学习动机与高阶思维，从而实现深度理解、深度探究、深度思维、深度体验.［3］

4.2以大单元理念为指引，组织单元复习

复习课的教学更应该以大单元理念为指引，引导学生将知识和方法嵌入到完整的知识体系中，特别是具备核心作用的内容.例如直线与方程这一章节作为学习解析几何的开篇，其载体作用在复习过程中应该深入挖掘，呈现给学生，让学生树立研究过程中的“整体观”.解析几何中对于直线研究的方式是通过建立方程研究其性质，对于其他的曲线也是如此，让学生对于解析几何的学习有一个整体认识，而这些研究过程的开展又是解析几何思想的本质所在：通过坐标系将几何问题转化为代数问题，而后又通过代数问题的解还原为几何对象的性质.在复习教学过程中老师要有大单元的理念，学生才会在数学學习中有方向，有需求，有价值体验，形成核心素养.

参考文献：

［1］吕世虎.单元教学设计及其对促进数学教师专业发展的作用［J］.数学教育学报，2016（10）：16-21.

［2］郭华.深度学习及其意义［J］.课程·教材·教法，2016（11）：25-32.

［3］卢光.高中数学深度学习与深度教学研究述评［J］.中学数学教学参考（上旬），2021（10）：73-75.

基金项目：江苏省教育科学“十四五”规划办重点课题《大概念视角下的高中数学单元整体教学实践研究》（课题编号：B/2021/02/28）．