基于联通图和线性规划的震后灾民转移安置模型研究
2023-07-21邓树荣周建荣肖鑫施建明陆亚波王林岚罗嘉铮
邓树荣 周建荣 肖鑫 施建明 陆亚波 王林岚 罗嘉铮


摘要:根据联通图与线性规划相结合的原理,构建了一种震后灾民转移安置模型。模型采用Floyd算法计算了灾民点到安置点最短路径,采用约束条件下的线性规划计算了最优安置人数,使得震后灾民转移路径最短,用时最少,安置人数分配最优。以云南省建水县临安镇为例,在城区遭遇Ⅷ度破坏的情况下,对灾民转移安置路径和人数分配进行演算,得到了优化的灾民转移安置方案,验证了模型的可行性。
关键词:联通图;线性规划;地震;转移安置
中图分类号:P315.95文献标识码:A文章编号:1000-0666(2023)03-0385-09
doi:10.20015/j.cnki.ISSN1000-0666.2023.0042
0引言
地震具有突發性,大部分人震后第一反应就是快速撤离到空旷的地方和应急避难场所。震后房屋倒塌,水、电、气、粮食等中断,加之余震不断,灾民恐慌,不敢也不愿回家,应急转移和避难需求成倍增加。2008年四川汶川8.0级地震,1993.03万人失去住所(汶川特大地震四川抗震救灾志编纂委员会,2017)。2010年青海玉树7.1级地震,1.5万户民房倒塌,灾区有10万户灾民需要转移安置。2014年云南鲁甸6.5级地震造成大量的房屋倒塌,截至8月18日,紧急转移安置25.4万人(皇甫岗,2015)。2021年云南漾濞6.4级地震导致约21902人失去住所,2万多人等待转移安置①。2021年青海玛多7.4级地震造成果洛、玉树州、海西州8县45个乡镇38137户107500人受灾,政府设置集中安置点126个。2022年四川芦山6.1级地震,四川省抗震救灾指挥部设置转移安置点61个,紧急转移安置受灾群众12722人。可见,地震造成了大量的灾民流离失所,当重大灾难性突发事件发生时,在短时间内安全地大范围疏散转移高密集人群,合理规划安置方案,实施科学的应急救灾策略,是减轻灾害后果严重性的重要措施之一(蔡娜等,2019)。为了保证群众安全,将人群快速疏散到安全区域,减小灾害造成的损失,制定合理、高效的灾时、灾后人群疏散策略及应急方案十分关键(钟光淳等,2022)。
转移安置点是指临时或提前规划建设的专门用于安置受灾群众的场所,其中应急避难场所是应急避险安置点的重要组成部分(王丹丹,徐伟,2018)。我国地震应急避难场所大多选择公园、绿地、广场、体育场馆和学校操场等作为场地,进行相应配套设施建设(杨爽等,2013;郭兴利等,2017)。震后,应急指挥决策部门通常会把灾民集中的居民区、学校、医院、村庄等作为重点转移区,市民广场、学校操场、体育场馆、公园、空旷地等被划定为震后应急避难场所或灾民安置点。避难场所具备“平、灾”两用的性质,其数量、位置与人口避难需求分布并不能完全匹配,会引起灾时应急转移人员分配的不均衡,从而导致转移滞后甚至无法转移的状况(魏本勇等,2022)。缺少科学合理的紧急避难转移安置方案,将造成灾区应急处置的混乱与无序,甚至激发社会矛盾。因此,一些学者对震后转移安置和应急转移进行了研究,如王女英等(2017)、苏建锋和张庆斌(2021)对城市应急避难场所服务功能的适宜性、空间分布与人口的匹配性进行了宏观研究;谢旭阳(2007)根据灾害发生时应急疏散范围,利用GIS将需要疏散的建筑物标识出来,建立了应急疏散最优模型;和仕芳等(2023)利用无人机航拍2021年云南漾濞6.4级地震灾区影像,使用加权泰森多边形法对应急避险安置点责任区划分进行了研究;曹彦波等(2008)基于GIS技术对地震应急异地转移接受能力判断模型进行了研究;魏本勇等(2022)研究了基于避难场所容量限制的地震应急转移路径规划,采用Dijkstra算法计算疏散需求点与目的地点的最短距离矩阵;叶永和赵林度(2011)对重大危险源大规模人群转移决策模型进行了研究,采用待疏散点-临时疏散救援点-医疗救治点两阶段疏散模式;李永义等(2011)对交通生命线系统震后应急调度模型及方法进行了研究,建立了震后多需求点多服务点应急调度的线性规划数学模型;刘小婵等(2014)基于GIS与多智能体的人群转移进行了模拟,建立了城市重大危险源灾害应急疏散决策模型。
以上研究为突发事件人员转移提供了理论支撑和实践参考,但这些研究大多为宏观对策研究,在应用中缺乏可操作性,部分研究仅考虑了最优转移路径,未给出转移人数,或者考虑了最优转移人数而未给出转移路径,或给出了定性的转移对策和情景模拟,但无法给出定量化的转移安置方案。鉴于此,本文结合联通图理论和线性规划的基本原理,对震后灾民转移安置进行数学模型研究和探讨,并给出定量化的最优转移路径和人数。
1模型构建基本思路
图是将客观世界中的某些事物之间的联系进行数学抽象,由2个要素组成,分别是结点和边。因此,图可定义为G={V,E},V表示图的结点,E表示连接结点的边,其中结点集合为V={v1,v2,…,vn},结点与结点连接的边集合为V={e1,e2,…,em}(殷剑宏,吴开亚,2006)。
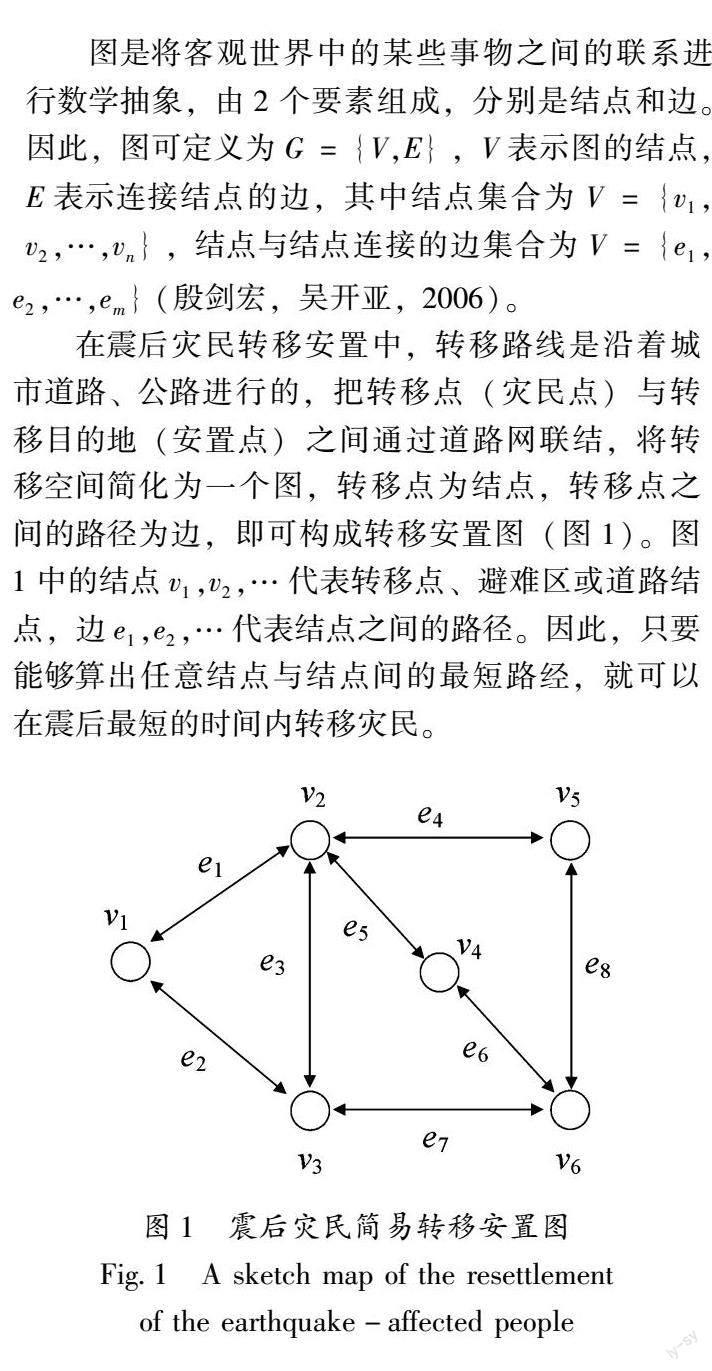
在震后灾民转移安置中,转移路线是沿着城市道路、公路进行的,把转移点(灾民点)与转移目的地(安置点)之间通过道路网联结,将转移空间简化为一个图,转移点为结点,转移点之间的路径为边,即可构成转移安置图(图1)。图1中的结点v1,v2,…代表转移点、避难区或道路结点,边e1,e2,…代表结点之间的路径。因此,只要能够算出任意结点与结点间的最短路经,就可以在震后最短的时间内转移灾民。
在灾民转移安置过程中,需要转移的人员规模和应急避难场所(安置点)位置、容量是不匹配的,不是一一对应的。针对该问题,可采用运筹学中的线性规划进行灾民转移安置人数的优化分配。建立灾民转移安置线性规划模型时,需要满足一些约束条件,主要有转移人员的位置、规模,避难场所的位置、容量等,最优目标为满足约束条件下转移安置距离最短、时间最少。
2模型建立
2.1转移安置影响因素
震后转移安置问题可描述为将转移安置人员以路径最短、人数最优的方式转移到应急避难场所。
(1)转移安置人数。转移安置人员是指震后因房屋受损倒塌无法继续居住而失去住所的人员,或者因震后生产生活资料无法满足需求,难以生活自理的弱势群体和受伤灾民。这里需要与房屋完好或受损较轻,因一时恐慌而进行应急疏散、应急避险的人员区别开来。这类人群的房屋通常可以继续居住,生产生活资料可以继续供给,政府部门只需对其进行地震应急科普宣传,动员劝返即可恢复正常生产生活秩序。因此,可以根据当地的人口基数、房屋数量、房屋类型、地震烈度等计算转移安置人数。
(2)应急避难场所容量。现行地震应急体制机制下,政府部门通常会在日常应急准备工作中根据人口规模在相应的地方规划建設应急避难场所,或者在震时征用一些空旷的农田、厂矿、工地等平整的空地搭建临时安置点。这些应急避难场所和临时安置点的场地面积、容纳人数即为应急避难场所容量。
(3)转移安置路径和人员分配。通常情况下,从灾民点到安置点会有多条道路,这些道路可以是城市道路、公路甚至乡村小道,都可以作为转移安置路径。震后不同地点的转移安置需求人数有多有少,不同的避难场所容量也不一样,这就需要对安置人数进行分配,将灾民合理地转移到不同的应急避难场所。
(4)转移安置目标。转移安置的目标主要包括:转移路径最短、用时最短及安置人数最优。
2.2最短路径模型
(1)转移安置路径规划
选定灾区范围,以灾区地图作为规划底图(图2a)。根据灾区地图中的道路交通网络,标注转移区和避难区,得到宏观的灾民点、安置点与灾区道路交通的拓扑图(图2b)。根据该位置关系图抽象成数学意义上的转移安置图,将灾民点、安置点、道路结点作为图的结点,将道路作为图的边,得到转移安置路径图(图2c)。
3实例验证
临安镇是建水县城所在地,下辖19个村、8个社区和1个农场,常住人口197097人。城市建成区面积19.6km2,城区人口127847人,人口密度为6523人/km2。建水及其周边区域分布有红河断裂、曲江断裂、石屏—建水断裂。自有历史地震记载以来,建水县共发生5.0级以上破坏性地震12次,其中1588年8月9日建水曲溪7.0级地震震区最高烈度大于Ⅸ度,死亡人数甚众。1970年通海7.8级大地震造成15621人死亡(张方浩等,2022)。2020年,云南省地震局对建水县进行了精细化的地震灾害风险评估,收集了大量详实的数据。基于此,本文选取建水县临安镇城区进行实例验证。
3.1最短路径
本文选取临安镇城区作为转移安置路径规划区域,定义灾民点为社区所在地,安置点为应急避难场所,以点要素的形式表达;转移安置路径为连接灾民点和安置点的道路,以线要素的形式表达,最终得到临安镇城区转移安置路径规划图(图3)。边权赋值主要利用91卫图距离测量工具测量出所有相邻可达结点之间的距离,得到结点距离矩阵。
根据构建的模型,采用floyd算法求解任意两点间的距离。通过Matlab算法编程,计算出临安镇城区各灾民点到安置点的最短距离矩阵(表2)和最短路径矩阵(表3)。
3.2最优人员分配
3.2.1基础数据及参数
计算临安镇城区的转移安置人数,需要人口、房屋基础数据(表4)以及破坏比(表5)、震亡比等参数。人口、房屋基础数据来源于2020年建水县地震灾害风险评估收集的数据云南省地震局.2020.红河州建水县地震灾害损失风险评估和应急处置要点报告.。建水县房屋破坏比采用滇南地区遭遇地震烈度Ⅷ度灾害时的破坏比卢永坤.2018.地震科技星火计划项目——云南省地震灾害区域特征研究项目研究报告.。死亡人数采用云南震亡比模型(曹彦波,李永强,2021)计算:
3.2.3应急避难场所容量
应急避难场所的最大容纳人数由应急避难场所的设计容量决定。临安镇城区应急避难场所设计容量见表7,数据来源于2020年建水县地震灾害风险评估收集的数据云南省地震局.2020.红河州建水县地震灾害损失风险评估和应急处置要点报告.。
3.2.4最优人员分配模型线性规划
将表6、7的数据带入式(6)~(8)建立建水县临安镇最优人员分配的线性规划模型。对该线性规划模型算法进行LINDO编程,计算得出临安镇城区转移灾民点到安置点的最优转移人数(表8)。
3.3灾民转移安置方案
根据最短路径计算结果(表2、3)和最优转移安置人数分配结果(表8),整理得到临安镇城区遭遇Ⅷ度地震烈度的灾民转移安置方案(表9),包括转移人数、转移路径、转移距离、转移用时,其中转移用时以成人步行4500m/h的速度计算。表9以(S1,B2)=3434、671、0.15和S1B2为例,3434表示疏散人数,671表示最短距离,0.15表示最短用时,S1B2表示转移路径。将表9转移安置方案中的转移路径绘制到临安镇城区地图上,标绘社区驻地、避难场所等要素,得到转移安置路径图(图4)。
4结论
本文讨论了基于联通图和线性规划的震后灾民转移安置模型构建过程,将复杂的震后灾民转移安置情景归纳为解决转移路径、人数分配2个问题。结合联通图和线性规划,给出定量化的震后灾民转移安置最优转移路径和人数分配模型。以建水县临安镇为例进行了实例验证,验证了模型的科学性和可操作性。
为了研究方便,本文定义的路径结点只有灾民点和安置点2种,在一些大城市和路网密集地区,可根据需求建立更多的路径结点,得到更短的疏散路径和更优的转移方案。在计算最优人员分配时,本文模型假设条件为灾民总人数小于等于避难场所总容量,反之则会出现疏散到避难场所的人数过多而“撑死”和过少而“饿死”的情况,需建立货机平衡的约束条件。模型决策目标的最短用时是为寻求疏散用时最短而假设的,实际疏散过程中并非所有灾民同时疏散或依次疏散,可建立其它模型加以讨论。本文构建的模型应用场景是灾民转移安置,在震后应急处置中,可以应用于物资调配、救援力量派遣等涉及路径规划和人员物资分配等场景,可根据需要对模型进行改进和附加一些条件。本文的模型算例临安镇位于城区,公园、市民广场、学校、医院等拥有开阔场地的公共场所较多,应急避难场所充足。震后山区乡镇和偏远村庄也是转移安置的重点区域,需考虑更多的灾民点和安置点。在震后转移安置中,山区道路会发生塌方、阻塞、中断等,城市道路会存在工程施工、管道泄漏、道路破坏等,指挥调度时还需要考虑道路交通阻抗的因素。
参考文献:
蔡娜,端木祥玲,詹子娜,等.2019.浅析重大耦合突发事件大规模人员转移安置技术研究进展[J].灾害学,34(1):167-171.
曹彦波,李永强,曹刻,等.2008.基于GIS技术的地震应急异地疏散接受能力判断模型研究[J].地震研究,31(S2):623-628.
曹彦波,李永强.2021.云南市县地震应急快速评估与辅助决策系统培训教程[M].昆明:云南出版集团公司.
郭兴利,郭雪琦,卓海涵,2017.城市地震避难所空间选址适宜性评价方法研究——以台中市西屯区为例[J].防灾科技学院学报,19(4):71-79.
和仕芳,张方浩,杜浩国,等.2023.加权泰森多边形在2021年云南漾濞MS6.4地震后应急避险安置点责任区划分的应用[J].地震研究,46(1):1-10.
皇甫岗.2015.2014年云南鲁甸6.5级地震[M].昆明:云南出版集团公司.
姜启源,谢金星,叶俊.2003.数学模型(第三版)[M].北京:高等教育出版社.
李永义,李伯权,储浩.2011.交通生命线系统震后应急调度模型及方法[J].南京工业大学学报(自然科学版),33(1):33-37.
刘小婵,张明锋,张正祥,等.2014.基于GIS与多智能体的人群疏散模拟[J].地理信息世界,21(5):105-110.
苏建锋,张庆斌.2021.城市地震应急避难场所适宜性评价——以天津市中心城区为例[J].震灾防御技术,16(2):414-420.
王丹丹,徐伟.2018.自然灾害应急安置点设置模式初探[J].灾害学,33(1):190-195.
王女英,修春亮,魏冶.2017.沈阳城市应急避难场所的识别、空间格局与服务功能[J].地域研究与开发,36(5):75-79,86.
魏本勇,董翔,谭庆全,等.2022.基于避难场所容量限制的地震应急疏散路径分析[J].地震研究,45(1):141-149.
汶川特大地震四川抗震救灾志编纂委员会.2017.汶川特大地震四川抗震救灾志·总述大事记[M].成都:四川人民出版社:6-35.
谢旭阳.2007.基于GIS的重大事故应急疏散决策研究[J].中国安全生产科学技术,14(2):32-35.
杨爽,张楠,赵士达,等,2013.天津市地震应急避难场所试点建设[J].防災减灾学报,29(4):79-82.
叶永,赵林度.2011.重大危险源大规模人群疏散决策模型研究[J].自然灾害学报,20(1):168-177.
殷剑宏,吴开亚.2003.图论及其算法[M].合肥:中国科学技术大学出版社.
张方浩,杜浩国,邓树荣,等.2022.以乡镇为单元评估云南省建水县地震灾害风险[J].地震研究,45(1):109-117.
钟光淳,翟国方,毕雪梅,等.2022.校园人群应急疏散行为及其影响因素研究[J].地震研究,45(1):150-159.
GB/T18208.4—2011,地震现场工作第4部分:灾害直接损失评估[S].
