基于Kekulé晶格非厄米系统拓扑边缘态的研究
2023-07-21徐炯臧小飞
徐炯 臧小飞


摘要:基于Kekulé晶格,验证了物质拓扑相与晶格原子间耦合作用之间的关系,研究了非厄米效应对拓扑绝缘体的影响。设计了两种格点增益损耗分布方式,分别说明了不同增益损耗对体态能谱、边缘态能谱的影响。随着增益损耗值的增大,体态能谱和边缘态能谱将经历能带间隙减小,能带在临界值处关闭形成狄拉克点,随后狄拉克点劈裂形成一对奇异点的过程。区别于传统对Kekulé晶格的研究,在保持系统胞内耦合作用相同的基础上,将胞间耦合作用分化为水平方向和垂直方向的两个量,分别进行调控,验证了拓扑边缘态能谱中能带间隙的有无不仅与几何边界相关,也受系统胞间耦合相互作用的调控。
关键词:Kekulé晶格;非厄米系统;拓扑边缘态;狄拉克点
中图分类号:O 433 文献标志码:A
Research on topological edge state in a non-Hermitian system based on the Kekulé lattice
XU Jiong1,2,ZANG Xiaofei1,2
(1. Shanghai Key Laboratory of Modern Optical System, University of Shanghai forScience and Technology, Shanghai 200093, China;
2. School of Optical-Electrical and Computer Engineering, University ofShanghai for Science and Technology, Shanghai 200093, China)
Abstract: The relationship between the topological phase of matter and interactions of the system was confirmed for the Kekulé lattice. The impact of non-Hermitian effect on topological insulator was investigated. Two types of gain and loss configurations were designed to illustrate their effects on bulk energy spectra and edge energy spectra. It is found that the bandgap decreases with the increase of the gain and loss, and is eventually closed and forms a non-Hermiticity-induced Dirac point. Finally, the Dirac point splits into a pair of singular points. Distinguishing from traditional Kekulé lattice, intercellular coupling is differentiated into horizontal and vertical dimensions for independent control based on the same intracellular coupling. This approach verifies that thegapless edge mode is not only related to geometric boundary, but also regulated by the intercellular coupling of the system.
Keywords: Kekulé lattice;non-Hermitian system;topological edge state;Dirac point
引言
20世纪,随着整数量子霍尔效应[1-2]被发现,拓扑作为近代数学分支,被引入凝聚态物理领域,并逐渐发展成为一门独立的学科——拓扑电子学。随后,人们将拓扑电子学类比到光学领域,将其发展成为拓扑光子学,为揭示物质拓扑相开辟了新的方向[3-4]。依据拓扑相的不同,人们将绝缘物质划分为非平庸拓扑绝缘体和平庸拓扑绝缘体。一种拓扑相连续转变至另一种拓扑相必将经历能带间隙打开—关闭—再打开的过程,即拓扑相变[5]。根据体边对应,两种拓扑相不同的光子晶体堆叠在一起时,其交界面会产生一种沿着体系边缘单向传输的边缘态。该边缘态受拓扑保护,无背向散射,被称为拓扑边缘态[6]。拓扑边缘态出现在体系公共带隙区域,以导模的形式存在。研究表明:在时间反演对称性被打破的体系中,体系能带中会出现一条横跨整个带隙的导模,即边缘态[7-8];在受时间反演对称性保护的体系中,体系能带中会出現成对的拓扑边缘态,如螺旋边缘态[9-10]、手性边缘态[11]等。研究发现,在体系带隙中,成对的拓扑边缘态是否会产生无间隙的狄拉克点,通常与边缘态所在界面的几何结构有关[12]。
相较于厄米系统,非厄米系统下的光子晶体具有复数形式的本征值及本征向量,这极大丰富了拓扑绝缘体的可研究内容。奇异点是一对本征值实数部分重合的兼并点,它的存在是非厄米系统的显著特征之一[13-14]。奇异点的出现引发了诸多奇特的物理现象,如奇异环[15]、体费米弧[16]、半整数拓扑电荷[17]。此外,结合多样的光子晶体结构,非厄米系统下的拓扑绝缘体引起了人们的广泛关注。本文将结合Kekulé晶格,研究非厄米系统的拓扑边缘态。相较于传统的蜂窝晶格,Kekulé晶格最近邻原子间的耦合作用可区分为胞内耦合和胞间耦合作用[18-19]。当胞间耦合强度大于胞内耦合强度时,系统为拓扑非平庸态;而当胞间耦合强度小于胞内耦合强度时,系统为拓扑平庸态。根据交界面的几何形状,两态交界面处产生的拓扑边缘态可分为 Zigzag 边缘态和 Armchair 边缘态。其中 Zigzag 边缘态受系统镜面对称保护,呈现出无间隙的狄拉克点,而 Armchair 边缘态不具有对称性,在其边缘态能谱中呈现出有间隙的两条边缘态谱线。以往针对Kekulé晶格拓扑边缘态的研究通常聚焦于厄米系统[20],或单一胞间耦合相互作用下的非厄米系统[21]。本文基于Kekulé晶格,在保持胞内耦合作用相同的基础上,将胞间耦合作用分化为垂直方向和水平方向的量,研究了非厄米系统下几何边界对拓扑边缘态的影响,丰富了该晶格的研究内容。
1 模型
蜂窝晶格由6个相同的原子构成,且原子均匀地分布在正六边形的6个顶角。而原子间的相互作用可以通过调控其相对位置来实现,即两个相互耦合的最近邻原子间距离越大,其相互作用越小;反之,则其相互作用越大。在蜂窝晶格的基础上,通过区分胞内耦合和胞间耦合的相互作用,可构建Kekulé晶格。传统厄米系统下的Kekulé晶格的胞内耦合和胞间耦合存在竞争关系:当胞内耦合和胞间耦合相等时,整个晶格具有 C6对称性,其体态能带图中出现一个狄拉克点,此时体系为狄拉克半金属的状态;当胞内耦合小于胞间耦合时,狄拉克点被打开,体态能带图中出现能带间隙,此时体系拓扑相为非平庸拓扑绝缘体;当胞内耦合大于胞间耦合时,体态能带图中出现能带间隙,此时体系拓扑相为平庸拓扑绝缘体,即普通绝缘体。
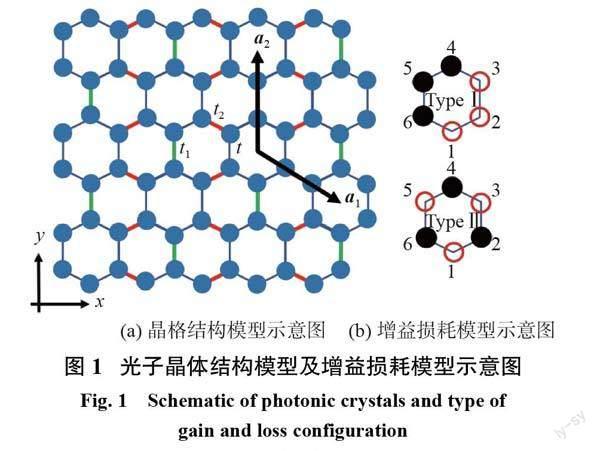
首先,基于Kekulé晶格讨论厄米系统中的拓扑相。Kekulé晶格结构如图1所示:蓝色实心圆代表Kekulé晶格格点上的原子;蓝色实线代表最近邻原子间的胞内耦合相互作用;绿色和红色实线均代表最近邻原子间的胞间耦合相互作用。通过改变原子间的相对距离来调控对应的耦合作用的强度。相较于传统蜂窝晶格的正六边形单胞,因为胞间耦合的作用,Kekulé晶格的单胞可形成7个正六边形亚晶格,从而具有更大的单胞形式。将Kekulé晶格中亚晶格的正六边形的边长设为晶格常数a,晶格矢量a1= a(3/2, - p3/2), a2= a(0, - p3)。假定胞内耦合相互作用为 t ,垂直方向上的胞间耦合相互作用为 t1,水平方向上的胞间耦合相互作用为 t2。基于紧束缚模型[22],采用厄米系统下哈密顿量 H来描述Kekulé晶格单胞内最近邻原子间的相互作用
式中:< i, j >为晶体中最近邻的两格点;tij为原子 ci和cj之间的相互耦合作用; ci ?为格点i产生的算符。
当原子 ci , cj之间的相互作用为胞内耦合时,tij = t ;当原子 ci , cj之间的相互作用为垂直方向上的胞间耦合时,tij = t1;当原子 ci , cj之间的相互作用为水平方向上的胞间耦合时,tij = t2。由此可得到非厄米系统相互耦合作用的哈密顿量核心矩阵
矩阵中 k 表示倒格子空间矢量。
设定矩阵元素的具体参数值后,求解其本征值,即可得到系统的体态能谱,如图2所示。在此默认 t =1,图2(a)中,取 t1=0.2,t2=0.9;图2(b)中,取 t1=2.0,t2=2.0;图2( c)中,取 t1=2.2,t2=2.9;图2(d)中,取 t1=2.9,t2=2.2。由图2可知:当 t1* t2时,单胞能带图关于零能级水平线上下对称,并处于半填充状态;当 t1= t2时,能带在布里渊区高对称点Γ和 K 处两两兼并,形成一对能带兼并点。
与非互易耦合的二聚化晶格(Su-Schrieffer- Heeger, SSH)类似,Kekulé晶格的拓扑相与胞内耦合和胞间耦合作用有着密切的关系,且胞内耦合作用和胞间耦合作用之间存在竞争关系,即:当胞内耦合强度大于胞间耦合强度时,系统呈拓扑平庸态;当胞内耦合强度小于胞间耦合强度时,系统呈拓扑非平庸态。为了验证这一猜想,采用图2中的各耦合作用参数,构建图1所示纳米带结构,进行拓扑边缘态的仿真,根据能谱间隙中边缘态的有无来判断体系是否为拓扑绝缘体。根据边缘态几何位置的不同,可将拓扑边缘态划分为 Armchair 和 Zigzag两种。分别绘制其边缘态能谱,如图2(a)和(b)中第2行(Armchair)和第3行(Zigzag)所示。可以看到:图2(a)中 t1< t , t2< t ,体系为拓扑平庸绝缘体,无法产生拓扑边缘态;图2(b)中, t < t1= t2,体系受镜像对称和几何结构手性对称性保护,并,其 Zigzag拓扑边缘态在中心点处发生兼产生无带隙的狄拉克点;图2(c)~(d)中,t < t1,t < t2,t1* t2,由于水平方向和垂直方向的胞间耦合作用不同,体系镜像对称被打破,原有的狄拉克点不再受几何对称性保护,故产生带隙,两条 Zigzag 边缘态不再兼并。由于 Armchair 拓扑边缘态所处的几何结构本身不具有对称性,故在 t1= t2, t1* t2的两种情况下均无法形成狄拉克点,边缘态能谱中均存在带隙,耦合作用的调控无法使能带间隙关闭以形成狄拉克点,具体边缘态能谱如图2所示。
2 非厄米效应
通过在原子中添加增益损耗来实现非厄米效应,增益损耗分布方式如图1(b)所示。将亚晶格内6个格点按照逆时针方向依次编号,在两种不同类型中,均对黑色实心圆圈所示格点上的原子施加增益,取+iγ(γ>0);对红色空心圆圈所示格点上的原子施加损耗,取-iγ(γ>0)。对于非厄米系统,用哈密顿量的核心矩阵来重新描述系统原子间的相互作用
为了验证非厄米效应对体态能谱的影响,根据哈密顿量的核心矩阵求解能量本征值,如图3所示,蓝色实线代表本征值的实数部分,绿色虚线代表虚数部分。图3(a)中, t1=1:2,t2=2:7,γ的取值从上至下依次为0:1,0:2,0:3;图3(b)中, t1=2:7,t2=1:2,γ的取值从上至下依次为0:100,0:358,0:500;图3(c)中, t1=1:2,t2= 2:7,γ的取值从上至下依次为0:1,0:2,0:3;图3(d)中, t1=2:7,t2=1:2,γ的取值从上至下依次为0:100,0:563,0:800。其中,图3(a)和(b)对应增益损耗 Type Ⅰ, 图3(c)和(d)对应增益损耗 Type Ⅱ。从图中可以看出:γ的取值相
对较小时,其对能谱整体影响不大;随着γ取值逐渐增大,其对能谱的调节作用逐渐明显,能谱带隙逐渐减小。当γ在体系中选取适当的特定值时,由于结构的几何对称性以及非厄米效应的影响,Type Ⅰ对应的图3(a)在高对称点Γ处出现狄拉克点,图3(b)在高对称点M处出现狄拉克点,且关于零能级水平线上下对称; Type Ⅱ对应的图3(c)和(d)均在高对称点Γ处出现狄拉克点,但他们所对应的γ取值不同。当γ取值持续增大时,图3(a)中对应的狄拉克点随即劈裂为一对奇异点,图3(b)中的一对狄拉克点劈裂为两对奇异点,并且,此时能量本征值出现虚部,且虚部的能谱图为一个环形。
通过在图1(a)所示的Kekulé晶格中分别添加图1(b)所示的增益损耗 Type Ⅰ和 Type Ⅱ来构建非厄米系统。取 t1=2:7,t2=2:2,此时 t < t1; t < t2,且t1* t2。由前文可知,该系统为拓扑绝缘体,其 Zigzag 拓扑边缘态之间存在带隙,为非厄米系统。图4(a)中,γ取值分别为0:100,0:305,0:500;图4(b)中,γ取值分别为0:050,0:059,0:070。以 Zigzag 拓扑边缘态为例,分析非厄米效应对拓扑边缘态的影响。如图4所示,由于非厄米效应,体系边缘态能谱出现虚部。随着γ取值的增大,能带间隙逐渐减小,直至γ=0:305 (Type Ⅰ)或γ=0:059(Type Ⅱ)的临界值时,实部能谱带间隙消失,两条 Zigzag 边缘态能带在中心处兼并为狄拉克点,虚部能谱也逐渐丰富。当γ取值继续增大,实部能谱中原有的狄拉克点劈裂为一对奇异点,虚部能谱由于奇异点的出现,呈现出独特环状能谱。
为方便起见,取 t1= t2=1:6> t ,即胞间耦合作用大于胞内耦合作用时的场分布情况,来分析非厄米系统对拓扑边缘态场分布的影响,如图5所示。在未施加增益损耗,即γ=0时,体系为厄米系统,选取 Armchair边缘态频点,场分布如图5(a)所示。当γ=1时,体系为非厄米系统,选取同一频点,场分布如图5(b)所示。
通过厄米系统、非厄米系统的拓扑边缘态场分布对比可知,非厄米系统的引入会直接影响拓扑边缘态的场分布,厄米系统下仅有 Armchair 模式,在非厄米系统下会引入 Zigzag 模式,场分布呈现两种模式的混合态。
3 结论
基于Kekulé晶格,在保持胞内耦合 t 不变的基础上,将胞间耦合分化为垂直方向 t1和水平方向 t2两个量,验证了当 t1< t , t2< t 时,系统为拓扑平庸绝缘体,即普通绝缘体,不存在拓扑边缘态;当 t1> t , t2> t 时,系统为拓扑非平庸绝缘体,根据交界面的几何形状,其边缘态可划分为 Zigzag 和 Armchair 两种模式;当 t1= t2> t 时, Zigzag 边缘态受镜面对称保护,呈现无间隙的狄拉克点,而 Armchair 拓扑边缘态由于本身所在边界几何不对称,故体系胞间耦合相互作用的调控不会使能带间隙关闭形成狄拉克点。在Kekulé晶格的基础上,利用不同增益损耗(不iγ)的分布,引入非厄米效应。结果显示:随着γ取值的持续增大,系统边缘态能谱会经历能带间隙减小,能带虚部能谱逐渐丰富的过程;当γ取值处于某个临界值时,两条拓扑边缘态能帶兼并形成狄拉克点;随着γ取值进一步增大,狄拉克点劈裂成为一对奇异点。相较于传统的Kekulé晶格拓扑绝缘体的研究,本文增加了胞间耦合调控维度,丰富了非厄米系统下拓扑边缘态的研究内容,为非厄米系统下的拓扑绝缘体研究提供了一些研究思路。
参考文献:
[1] KLITZING K V, DORDA G, PEPPER M. New method for high-accuracy determination of the fine- structure constant based on quantized Hall resistance[J]. Physical Review Letters, 1980, 45(6):494–497.
[2] KOHMOTO M. Topological invariant and the quantization of the Hall conductance[J]. Annals of Physics, 1985, 160(2):343–354.
[3] LU L, JOANNOPOULOS J D, SOLJA?I? M. Topological photonics[J]. Nature Photonics, 2014, 8:821–829.
[4] LU L, JOANNOPOULOS J D, SOLJA?I? M. Topological states in photonic systems[J]. Nature Physics, 2016, 12:626–629.
[5] HALDANE F D M. Nobel lecture: topological quantum matter[J]. Reviews of Modern Physics, 2017, 89(4):040502.
[6] BERNEVIG B A, HUGHES T L, ZHANG S C.Quantum spin Hall effect and topological phase transition in HgTe quantum wells[J]. Science, 2006, 314(5806):1757–1761.
[7] WANG Z, CHONG Y D, JOANNOPOULOS J D, et al. Reflection-free one-way edge modes in a gyromagnetic photonic crystal[J]. Physical Review Letters, 2008, 100(1):013905.
[8] WANG Z, CHONG Y D, JOANNOPOULOS J D, et al. Observation of unidirectional backscattering-immune topological electromagnetic states[J]. Nature, 2009, 461(7265):772–775.
[9] KANE C L, MELE E J. Z2 topological order and the quantum spin Hall effect[J]. Physical Review Letters, 2005, 95(14):146802.
[10] KANE C L, MELE E J. Quantum spin Hall effect in graphene[J]. Physical Review Letters, 2005, 95(22):226801.
[11] LU J Y, QIU C Y, KE M Z, et al. Valley vortex states in sonic crystals[J]. Physical Review Letters, 2016, 116(9):093901.
[12] OCHIAI T, ONODA M. Photonic analog of graphene model and its extension: Dirac cone, symmetry, and edge states[J]. Physical Review B, 2009, 80(15):155103.
[13] CEJNAR P, HEINZE S, MACEK M. Coulomb analogy for non-Hermitian degeneracies near quantum phase transitions[J]. Physical Review Letters, 2007, 99(10):100601.
[14] HEISS W D. The physics of exceptional points[J]. Journal of Physics A: Mathematical and Theoretical, 2012, 45(44):444016.
[15] SHEN H T, ZHEN B, FU L. Topological band theory for non-Hermitian Hamiltonians[J]. Physical Review Letters, 2018, 120(14):146402.
[16] WAN X G, TURNER A M, VISHWANATH A, et al. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates[J]. Physical Review B, 2011, 83(20):205101.
[17] NAGAI Y, QI Y, ISOBE H, et al. DMFT reveals the non-Hermitian topology and Fermi arcs in heavy- fermion systems[J]. Physical Review Letters, 2020, 125(22):227204.
[18] HOU C Y, CHAMON C, MUDRY C. Electron fractionalization in two-dimensional graphenelike structures[J]. Physical Review Letters, 2007, 98(18):186809.
[19] BAO C H, ZHANG H Y, ZHANG T, et al. Experimental evidence of chiral symmetry breaking in Kekulé-ordered graphene[J]. Physical Review Letters,2021, 126(20):206804.
[20] FREENEY S, VAN DEN BROEKE J J, HARSVELDVAN DER VEEN A J J, et al. Edge-dependent topology in Kekulé lattices[J]. Physical Review Letters, 2020, 124(23):236404.
[21] XU QY, LIU F, CHEN C Z, et al. Edge states in a non- Hermitian topological crystalline insulator[J]. Physical Review B, 2022, 105(7):075411.
[22] SU W P, SCHRIEFFER J R, HEEGER A J. Solitons in polyacetylene[J]. Physical Review Letters, 1979, 42(25):1698.
(編辑:李晓莉)
