帕累托-有限推力航天器轨道机动问题中相对运动的最优控制
2023-07-20谢尔盖伊斯科夫格里果利菲利波夫周晓王长青
谢尔盖·伊斯科夫, 格里果利·菲利波夫, 周晓, 王长青
(1.萨马拉大学, 俄罗斯 萨马拉 443086; 2.西北工业大学, 陕西 西安 710072)
本文研究了在被动航天器附近,配有能够多次启动的有限推力发动机的主动航天器标称相对运动控制程序的优化问题。该问题在将航天器送至地球静止轨道站点、校正受扰动地球静止轨道参数以及构建巡检航天器的控制程序等方面具有重要的应用价值。在设计太空任务时核心问题是选择航天器标称控制程序,确定航天器及其运动控制系统的主要设计参数。在其解决方案中考虑的主要标准是机动时间成本和总时间成本。对于所考虑对象中由有限(非脉冲)推力连续控制的卫星,控制问题应使用双准则公式中的帕累托最优控制原理来解决。
多准则优化方法在相对运动控制问题中的应用早在文献[1-2]中就被考虑过。传统方法之一是通过准则的卷积将多准则问题简化为单准则问题,这在某种程度上降低了所获得解决方案的价值。 在本文中,目标不是获得一个单一的解决方案,而是获得一组详尽的不可改进的最优解决方案——帕累托集。
1 运动数学模型
对于没有施加控制约束的一般情况,轨道圆柱坐标系中的相对运动方程表示为[3]
(1)
式中:Δr为航天器半径向量差;Δu为航天器纬度参数的差值;Δz为侧向坐标差;ΔVr,ΔVu,ΔVz为航天器在径向、横向和侧向的速度差;r1,Vr1,Vu2为被动航天器的半径向量、径向和横向速度;r2,Vr2,Vu2为主动航天器的半径向量、径向和横向速度在被动航天器轨道平面上的投影;aS,aT,aW为主动航天器在径向、横向和侧向方向上的推力加速度。
被动航天器运动参数根据无扰动理论确定
(2)
式中,p,e,ϑ是半交弦、偏心率和真近点角。
引入假设:主动航天器和被动航天器的运动参数之间的差异与被动航天器的轨道半径相比较小,并且被动航天器轨道是圆形(e=0)。这将使方程(1)[4]线性化
(3)

将系统(3)写成矩阵形式
(4)
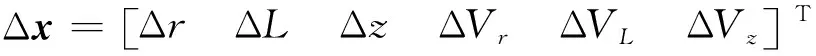
将柯西公式应用于动力学方程(3),得到了用于确定任意时刻t的相位向量表达式
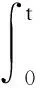
(5)
式中,Φ(t)为系统(3)解的基本矩阵,形式为[5]
Φ(t)=[a1,a2,a3,a4,a5,a6]T
(6)
式中:
方程(5)中的积分部分由矩阵的正交性求得
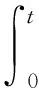
(7)
式中:
利用基本矩阵(6),可以用坐标形式写出被动运动方程,分析相对运动的性质:
1) 相对运动的纵向分量(Δr,ΔL,ΔVr,ΔVu)与侧向分量(Δz,ΔVz)无关;
2) 主动航天器在纵向平面中相对于被动航天器沿着椭圆运动,其半轴关系为2∶1;
3) 如果椭圆中心位于被动航天器的下方,椭圆中心将沿着主动航天器的运动方向移动;如果椭圆中心位于被动航天器的上方,椭圆中心与主动航天器的运动方向相反;
4) 侧向平面的运动表示为谐波振动。
在纵向相对运动中,区分了长期和周期性分量(见图1)。
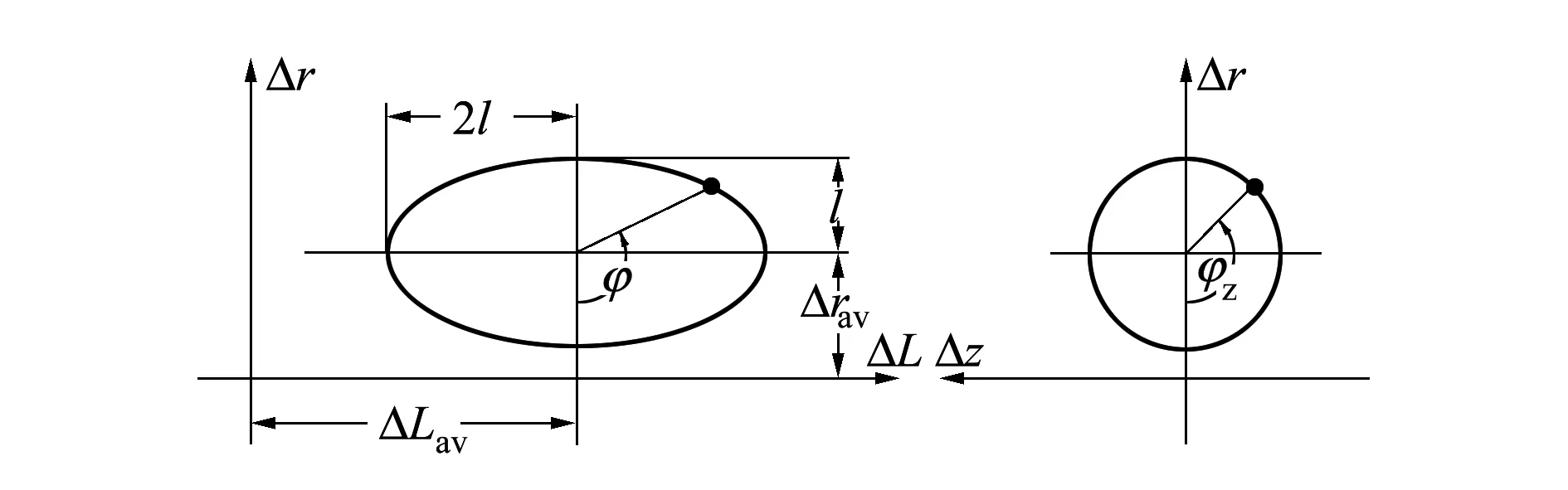
图1 运动的长期和周期性分量
将表征椭圆中心位移及其短半轴大小的参数视为长期参数,而将表征航天器在椭圆上位置的参数视为周期性参数。对于一般情况引入变量
(8)
式中:Δrav为主动航天器沿着被动航天器轨道半径的平均位移;ΔLav为主动航天器沿着被动航天器轨道的平均位移;l为相对运动椭圆的短半轴;lz为在侧向平面中的振荡幅度;φ和φz为确定主动航天器在相对运动椭圆上位置的角度。
写出变量(8)的微分方程。将左右部分对时间求微分,转换之后得到
(9)
系统(9)中的微分运动方程和正交解(7)允许在某些情况下简化对空间物体相对运动问题的研究。
在系统(9)中第4和第6个方程的右侧,由于l和lz分别位于分母项,这使得当它们数值较小时会产生计算困难,这是接近圆形的轨道的特征。在这种情况下,可以转换到变量
(10)
这些变量的微分方程采用以下形式
(11)
以最终形式写下适合研究近圆轨道的相对运动微分方程组
(12)
该系统的解析解是从求积方程组(7)的解中获得的,同时考虑了变量(8)和(10)[4]
(13)
在此指出
(14)
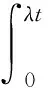
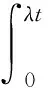
考虑用横向推力控制相对运动平面参数的问题。
写出无量纲形式的运动方程。为此,将系统(13)的前4个方程左右两边除以一个比例因子K=2aλ-2,得到
(15)
式中
以无量纲形式写下(13)式的解析解
(16)
(17)
使用解析解(16),定义相对运动的椭圆的短半轴正交解为
展开前面表达式中的括号,得到
(18)
此外,为了便于表示,下文中将省略变量上面的“-”符号。意思是所有的变量都是无量纲的。
2 具有双主动区域的控制程序设计
通过相对运动模型(15)和解析解(16),可以构造相对运动参数步进式控制和联合控制的标称程序和相对运动参数的联合控制。 现有研究表明,协同控制程序的参数计算将更加复杂,但它们在目标标准的最小值方面更具吸引力。
研究参数控制程序的联合控制问题,如图2所示。假设2个横向推力的符号为相同和相反2种情况。
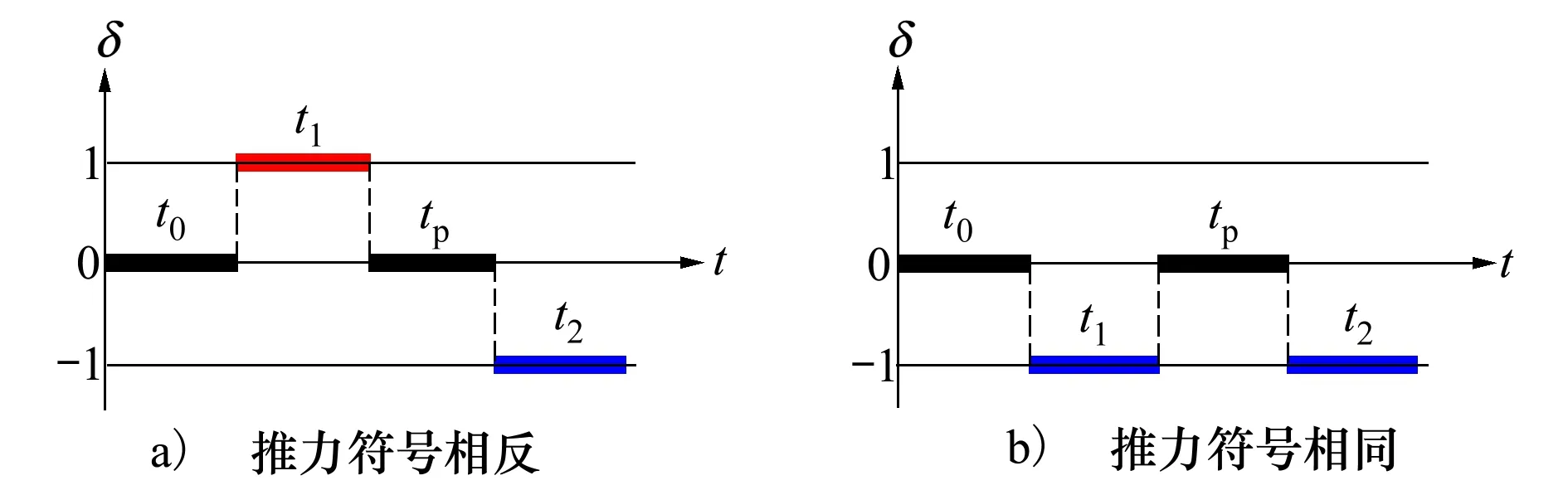
图2 控制结构
如图2所示,参数化程序由4个特征区域组成:
1) 限制在0~0.2π范围内的持续时间为t0的等待区域;
2) 持续时间为t1的第一个主动区域;
3) 持续时间为tp的被动区域;
4) 持续时间为t2的第二个主动区域;
概括地表述两准则优化的问题。需要确定满足边界条件的主动区和被动区的持续时间
(19)
t=tf:
Δrav=0, ΔLav=0,lx=0,ly=0
并提供最低的任务标准
(20)
式中:tmot是机动时间成本;tsum是总时间。
2.1 2个不同符号推力开关的程序优化
对于所考虑的控制结构,定义多项式A、B、C和D(参见(17)式),得到:
(21)
由解析解(16),考虑(21)式,定义边界条件与控制参数之间的关系,得到了主动区域的持续时间的方程
(22)
此处
考虑所研究的控制结构的多准则问题的特殊性,并写出问题(20)~(22)的准则
(23)
在不考虑相对运动椭圆的短半轴的边界条件的情况下考虑这个问题,并解析地定义帕累托集的边界。根据问题的标准tmot和tsum,表达参数tp,将获得:
(24)
(25)
通过等式(24)和(25)的右侧,得到了帕累托最优解集的边界
(26)
表达式(26)允许在等待区域持续时间固定时估计机动和总时间成本的上限和下限。
帕累托最优解(26)的集合由于被动区域非负性的条件被限制在右侧,对应于min(tsum):
(27)
由于主动区域的非负性条件的约束,帕累托最优解(26)的左侧同样受到限制,对应的条件为min(tmot):
min(tmot)=|Δrav0-Δravk|
(28)
确定等待区和被动区的持续时间。 对等式(18)的分析表明,对于所有边界条件,被动区持续时间t0和tp的最优值应满足条件sin(φ0+t+ξ)=±1,其中加号对应于相对运动椭圆的短半轴增加,减号对应于短半轴减少。 然后从等式(18)得到一个方程组
(29)
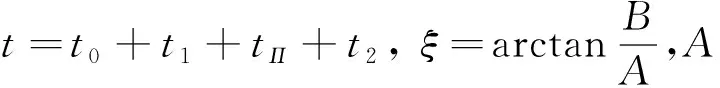
以参数t0和tp作为自变量在数值上求解方程(29)。 因此,多准则问题被简化为具有2个未知数t0和tp的2个非线性方程(29)的系统的解。 由于方程(29)右边包含调和函数,因此这个问题有几个解,应该选择其中的帕累托最优解。
2.2 2个同号推力开关的程序优化
对于所考虑的控制结构,定义多项式A,B,C,D(参见(17)式),得到:
A=-cos(t1+tΠ+t2)+
cos(tΠ+t2)-cos(t2)+1
B=sin(t1+tΠ+t2)-sin(tΠ+t2)+sin(t2)
C=t1+t2
(30)
由解析解(16),考虑(30)式,定义连接边界条件与控制参数的关系,得到主动区域持续时间的方程
(31)
其中主动区域的推力符号定义为
(32)
以参数Δrav,ΔLav为变量的(31)式满足边界条件。考虑多准则问题的特征,而不考虑相对运动椭圆的短半轴的边界条件。所研究的控制结构的问题(19)的标准将采用(33)式的形式
(33)
从(33)式可以看出,标准问题中,机动时间是恒定的,并且仅取决于标准问题的边界条件Δrav,总时间随着被动区域持续时间的增加而不断增加。
因此,正如从(33)式得出的,多准则问题退化为单准则问题,即由等式(29)~(31)确定被动和等待区域的持续时间,不仅满足了边界条件,且其值为最小值。
相对运动轨迹示例如图3~4所示。图3为坐标系中无量纲变量Δrav,ΔLav的运动轨迹。图4给出了相对运动椭圆的无量纲短半轴对时间的相关性的示例。在图3中,虚线对应于相对运动的长期性分量,实线对应于运动的周期性分量。
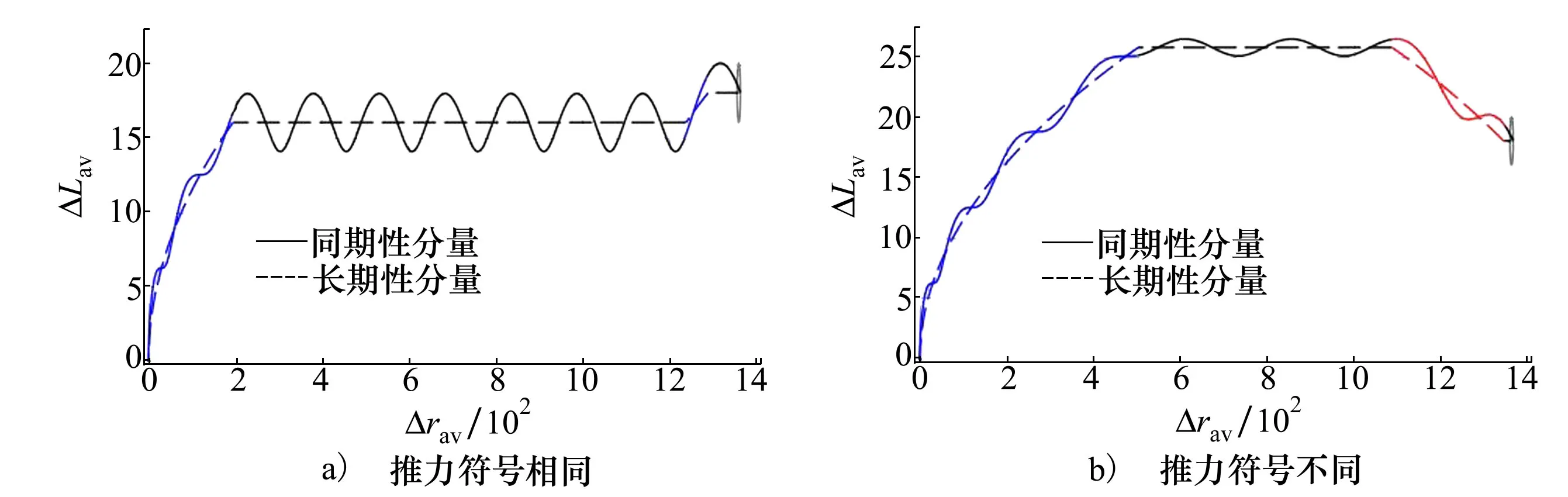
图3 无量纲变量Δrav,ΔLav的相轨迹示例

图4 相对运动椭圆的无量纲短半轴对无量纲时间的相关性示例
3 控制参数计算和帕累托集构建
考虑在(34)式边界条件下的问题的解
(34)
计算结果列于表1中。图5展示了一个帕累托集的示例。

表1 问题(33)的解
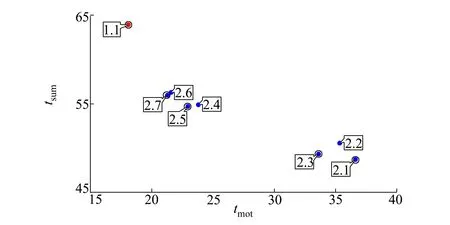
图5 问题(33)的解决方案,两次和三次推力开关的控制程序比较
注:序号1.1~1.3包含2个同号推力开关;序号2.1~2.7包含2个不同符号推力开关。
在图5中,帕累托最优解是序号为1.1,2.7,2.5,2.3,2.1的解。因此,该问题有5个解。帕累托集不是连续的,而是用点表示的,这是由于需要共同改变运动长期性和周期性分量,选择了严格定义的被动区域的持续时间。
图5中最左边的点对应于具有相同推力符号的程序提供的最小电机时间消耗。 其余点对应不同推力符号的程序,以增加机动时间为代价减少总时间。
请注意,解决方案2.1 对应于具有最小被动区域持续时间的程序。
如图5所示,集合的最左点1.1对应于运动时间的最小消耗,这是由具有相同推力符号的程序提供的。其余的点对应不同推力符号的程序,可以通过增加机动时间来减少总时间。注意,解决方案2.1对应于具有最小总校正时间的程序。
4 结 论
考虑了选择标称帕累托最优相对运动控制的问题。 在将相对运动分为长期运动和周期运动的基础上,开发了一种计算2个横向推力组成的结构控制参数的算法。 主动区域的持续时间由分析确定,被动区域持续时间由数值计算得到。正如研究表明的那样,控制问题有许多解决方案,它们的机动时间和总时间明显不同。 进行的研究表明在多标准公式中选择标称控制的必要性。
