例析几道竞赛组合题的解法

江西科技学院附属中学 (330000) 闵书存

江西省南昌市新建第一中学 (330103) 闵幼梅

组合数学中基本的问题之一是组合计数问题,这部分内容在高中数学中通过排列与组合这一章节进行考察,解决组合计数问题需要学生熟练使用常见的组合计数模型,能够灵活地设计分类与分步方法,充分利用对称思想,灵活地将计数问题进行转化,适当地使用正难则反的思想,建立m对n的对应关系等.本文以近年高中数学联赛一试中的组合计数问题为例,剖析其解答过程归纳组合计数问题常见的几种解答方法.

例1 在5×5矩阵中,每个元素都为0或1,且满足:五行的元素之和都相等,但五列的元素之和两两不等,这样的矩阵个数为________.(2022年全国中学生数学奥林匹克竞赛预赛A1卷第8题)

分析1：本题要求五列的元素之和两两不等,考虑到一列的和只能取0-5这六种情况,因此五列的列和是0、1、2、3、4、5这些数字中的5个,又考虑到五行的行和都相等,故矩阵中所有元素之和是5的倍数,经过这样的分析,我们得到五列的列和只能是0、1、2、3、4或者1、2、3、4、5这两种情况.

分析2：事实上,我们可以建立五列的列和是0、1、2、3、4这种情况和五列的列和是1、2、3、4、5这种情况的一一对应关系,只需将五列的列和是0、1、2、3、4这种情况中列和为0这一列全部填上1则唯一地对应成五列的列和是1、2、3、4、5这种情况.反之,将五列的列和为1、2、3、4、5这种情况中的列和为5这一列全部换成0,则唯一地对应成五列的列和是0、1、2、3、4这种情况,这表明两种情况的计数数量相同,因此只需计算其中一种情况的计数数量即可.

分析3：考虑列和为1、2、3、4、5的情况的填数方法数,利用对称性,五列的列和的排布方式总数量5!中的每一种对后续填数方法计数影响一致,故只需考虑图1中从左到右的列和顺序为1、2、3、4、5的情况.

分析4：又由于第一列的1放置在哪一行对后续计数影响一致,第5列已经全部填写了1,故只需考虑第1列的1放置在第一行的情形,此时的表格简化为只需考虑如图2所示的5×3的表格.

图2

分析5：考虑第四列的0应当放置在何处,可以分为两类,一类是0被放置在第一行,一类是0被放置在第二、三、四或者五行,后一类的四种情况对后续计数产生的影响一致,因此只需考虑其中一种情况即可.根据行和为3,部分位置的元素已经被确定,故接下来只需对以下图3、图4两种情况进行计数:

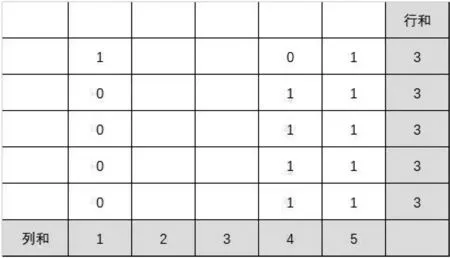
图3

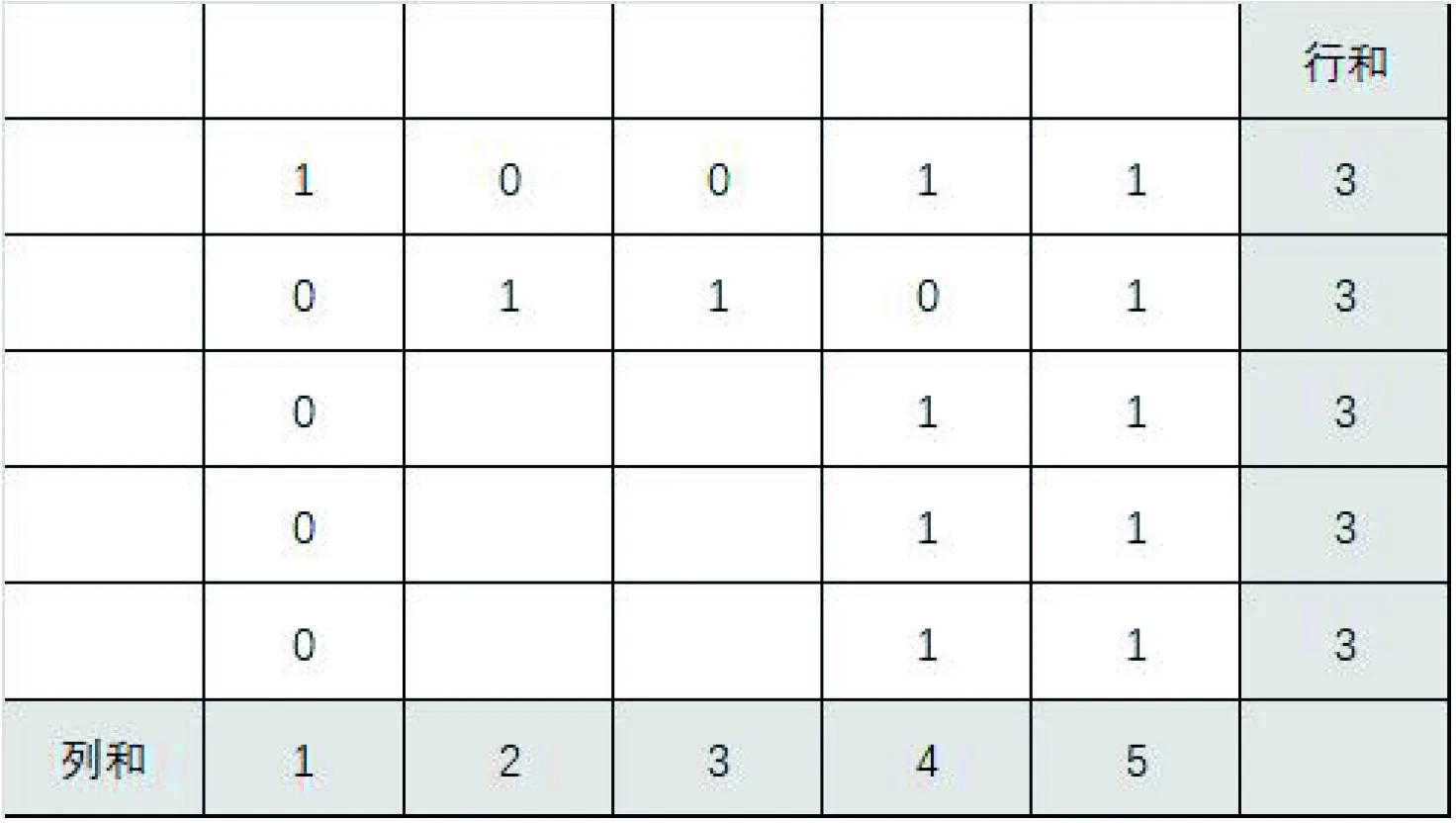
图4

点评：在本题的分析过程中,不断地通过对称思想简化要填写的表格,最后通过合理的分类与分步将问题解决,充分体现了对称思想在处理组合计数问题中的作用.

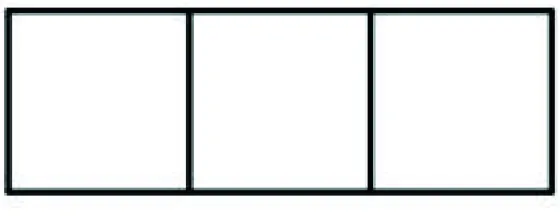
图5

例一个单位方格的四条边中，若有两条边染了颜色i，另两条边分别染了异于i色的另两种不同颜色，则称该单位方格是i色主导”的.如图)5，一个1×3方格表的表格线共含10条单位长线段，现要对这10条线段染色，每条线段染为红、黄、蓝三色之一，使得红色主导、黄色主导、蓝色主导的单位方格各有一个，这样的染色方式数为_________.(2022年全国中学生数学奥林匹克竞赛预赛A卷第8题)

分析1：为方便说明,我们对边进行如下的编号为如图6:

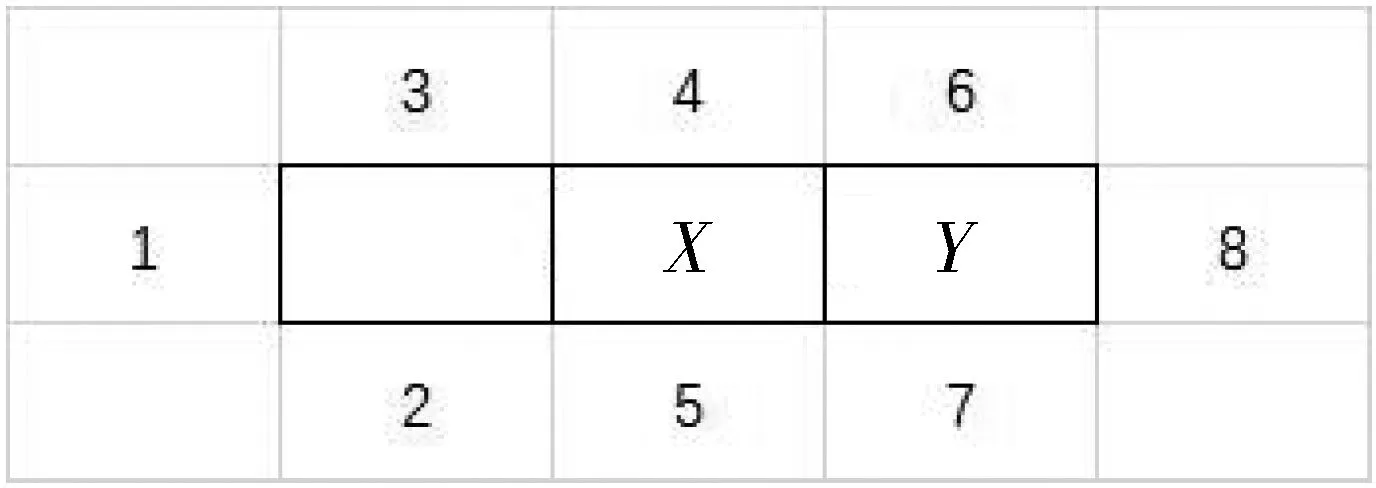
图6

由对称性,三个主导颜色的排列顺序对后续计数的影响是相同的,因此,只需考虑从左至右三个主导颜色的排列顺序为红黄蓝的情况.

分析2：观察10条边的特征,发现这些单位方格中的两条公共边最特殊,它们中的每一个都会对两个方格的染色方式产生影响,因此从对象的这一特征入手进行分类.考虑到中间的方格是黄色主导,因此,这两条公共边的颜色可以同时是黄色或者其中之一为黄色,或者二者均不为黄色.下面对这三种情况分别进行计数.

分析3：如果XY这两天边均为黄色,则边45可任意染成红色和蓝色即可,故方法数为2;由对称性,边123的染色方法数与边678的染色方法数相等.故只需考虑边123的染色方法数,只需确定蓝色边的位置即可,故方法数为3.综合可得此种情况下,染色方法数为2×3×3=18.

分析4：如果XY这两边其中之一为黄色,有三种情况需要考虑,分别是X和Y为黄色和红色、X和Y为黄色和蓝色、X和Y为红色和黄色、X和Y为蓝色和黄色,其中X和Y为黄色和红色这种情况与X和Y为蓝色和黄色这种情况具有对称性,X和Y为红色和黄色这种情况与X和Y为黄色和蓝色这种情况具有对称性,下面又分别考虑它们.

分析5：若X和Y为黄色和红色,则45应为黄蓝或者蓝黄,故染色方法数为2;123应当有两边为红,一边为蓝,故染色方法数为3.678应当由两边为蓝,一边为黄,故染色方法数为3;故这种情况下的染色方法数为2×3×3=18.

分析6：若X和Y为红色和黄色,则45应当有一边为黄,一边为蓝,故染色方法数为2;123应当是三个颜色,故染色方法数为3!=6;678应当有两边为蓝,一边为红,故染色方法数为3;故这种情况下的染色方法数为2×6×3=36.

分析7：如果XY这两边均不为黄色,则45必须均为黄色,此时有两种情况需要考虑,一种是XY为红色和蓝色,一种是XY为蓝色和红色;若XY分别是红色和蓝色,则123应当是三种颜色,故染色方法数为3!=6;678应当也是三种颜色,故染色方法数为3!=6,故总的染色方法数为6×6=36;若XY分别是蓝色和红色,则123应当有两边为红色一边为黄色,故染色方法数为3;678应当有两边为蓝色一边为黄色,故染色方法数为3,总的染色方法数为3×3=9.

综上分析可知,总的染色方法数为((36+9)+(36+18)×2+18)×3!=1026.

点评：解决该问题需要灵活地设计分类与分步方法,同时要充分利用对称思想减少复杂度.

例3 将6个数2,0,1,9,20,19按任意次序排成一行,拼成一个8位数(首位不为0),则产生的不同的8位数的个数为________.(2019年全国中学生数学奥林匹克竞赛预赛A卷第8题)

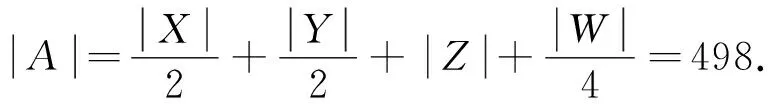
点评：本题通过构造两个集合的元素之间的映射关系,巧妙地解决了求解其中一个集合的元素的个数的问题,这种方法是解决组合计数问题的常见方法之一.

以上三道试题的剖析,演示了全国高中数学联赛的组合计数问题中几种常见的解答方法和解答思想,总体上,解决组合计数问题可以归纳为如下思路:(1)在理解问题的基础上将问题的主要特征提取出来;(2)考虑是否需要对问题进行适当转换;(3)根据提取的特征设置适当的分类与分步方式;(4)充分地利用对称思想减少讨论的情况数;(4)在细节处理上适当地使用正难则反的思想;(5)部分不方便计数的问题可以考虑建立集合与集合之间的映射关系.