隧底富水围岩脱空条件下重载铁路隧道动力响应
2023-07-18王登科骆建军王官清李飞龙侯艳娟
王登科,骆建军,王官清,李飞龙,侯艳娟
(城市地下工程教育部重点实验室(北京交通大学),北京 100044)
重载铁路以其高效率、低成本的特点受到世界各国广泛的关注和推广。由于重载列车轴重大、密度大、运输量大,运行过程中对隧道基底结构的影响也就较大[1]。据不完全统计,中国重载铁路病害率达76.83%,是一般铁路隧道的2.5倍,且主要集中在隧道底部[2]。基底脱空是隧道病害的表现形式之一,隧道基底富水时,基底围岩的含水量会从最佳状态转变为饱和状态,在循环动荷载作用下可能导致细颗粒过量抽送,从而使仰拱与围岩接触状态发生改变,久而久之,形成脱空[3-4]。隧底下方一旦出现空洞,基底结构的应力状态将类似于简支梁,较大的动应力和变形容易导致基底结构开裂,甚至引起车辆晃动,严重影响行车安全。
因此,开展列车荷载和地下水耦合作用下基底围岩脱空对隧道基底结构的动力响应研究具有重要意义。
目前,国内外学者针对脱空条件下重载铁路隧道基底结构的动力响应这一领域开展了大量研究。文献[5]建立了列车-隧道-围岩的三维动力学耦合模型,研究了不同脱空宽度下仰拱结构的动力响应并预测其疲劳寿命,得到基底极限脱空宽度为2 m。文献[6]采用室内试验与离散元模拟相结合的方法,分析了不同轴重和围岩条件下重载铁路隧道底部围岩劣化范围和深度,得到20 cm为围岩最大劣化深度。文献[7]采用数值模拟的方法,研究了基底不同脱空宽度和深度下仰拱结构的动力响应,得出脱空宽度不超过2 m可满足隧道使用年限要求。文献[8]采用数值模拟与弯曲疲劳试验相结合的方法,对脱空条件下基础结构的疲劳性能进行了研究,量化了空洞条件下隧底结构的疲劳损伤演化特征。文献[9]通过数值模拟研究了基底脱空对仰拱结构的影响,得到基底脱空时仰拱中心为拉应力最大值,边墙连接处为压应力最大值。文献[10]通过模型试验揭示了铁路底部翻浆冒泥的机理,得到底土中高孔隙水压力的消散导致了泥浆的抽吸,进而形成底部空洞。文献[11-12]通过现场监测和模型试验,对隧道基底不同土质下(黏性土、卵石土、砂质土)基底围岩脱空演变规律进行了研究,得到黏性土受列车荷载和地下水的影响最大。文献[13]以大瑶山隧道为例,将基底脱空分为内侧单边脱空、两侧对称脱空和中间扩展脱空,并指出当脱空宽度达到1.2 m时,基底结构将破坏。
总体来看,国内外学者对脱空情况下重载铁路隧道基底动力响应的研究取得了一定的进展。文献均提到脱空是地下水与列车荷载的耦合作用,但在研究列车荷载作用下隧底围岩脱空对隧底结构影响时,却未将地下水考虑其中。同时上述研究中,将空洞形状都简化为矩形,而实际情况下基岩脱空的形状是很不规则的[14]。鉴于此,本文结合已有相关研究,采用现场试验和数值模拟相结合的方法,分别以竖向位移、孔隙水压力和竖向动应力为评价指标,更为系统地研究了不同空洞形状(椭圆形、余弦形、矩形)下富水基底结构的动力响应特性,提出了较为符合实际的脱空形状,确定了富水软弱地层中隧道基底围岩的脱空阙值。
1 现场实测
1.1 测点工程概况
测点隧道位于山西境内,隧道岩性以长石砂岩、泥岩及砂质泥岩为主。隧道内Ⅳ、Ⅴ级围岩占到70.4%,水文地质条件复杂,地表水和地下水十分发育,且呈补给关系,局部地段,节理裂隙普遍发育,为地下水的补给以及渗透提供了良好的条件。该隧道为单洞双线重载铁路隧道,全部采用复合式衬砌。经现场调研,隧道自开通运营以来出现了不同类型的病害,其中以衬砌渗漏水、翻浆冒泥及基底吊空最为严重(图1),这些病害发生在隧道洞口和洞中地下水发育地段,以上行重车线最为严重,约有285 m发生了不同程度的病害。目前,列车通过该段时需降速行驶,基底病害已严重影响列车行车安全。

图1 重载铁路隧道主要病害
1.2 传感器布设
选择隧道V级围岩断面进行现场动应力测试,由于列车动荷载主要影响重载线路轨道正下方区域[15],因此,部分传感器被直接埋设在重载线路轨道正下方,以确定动荷载的竖向传播规律。其余传感器埋设在基底填充层表面,以研究动载荷的横向分布,传感器布设如图2所示。本次测试主要对27 t轴重的重载列车以80 km/h的速度通过隧道时的基底竖向动应力进行监测。为丰富试验数据,本次试验共采集了60次通过监测点的重载编组列车。
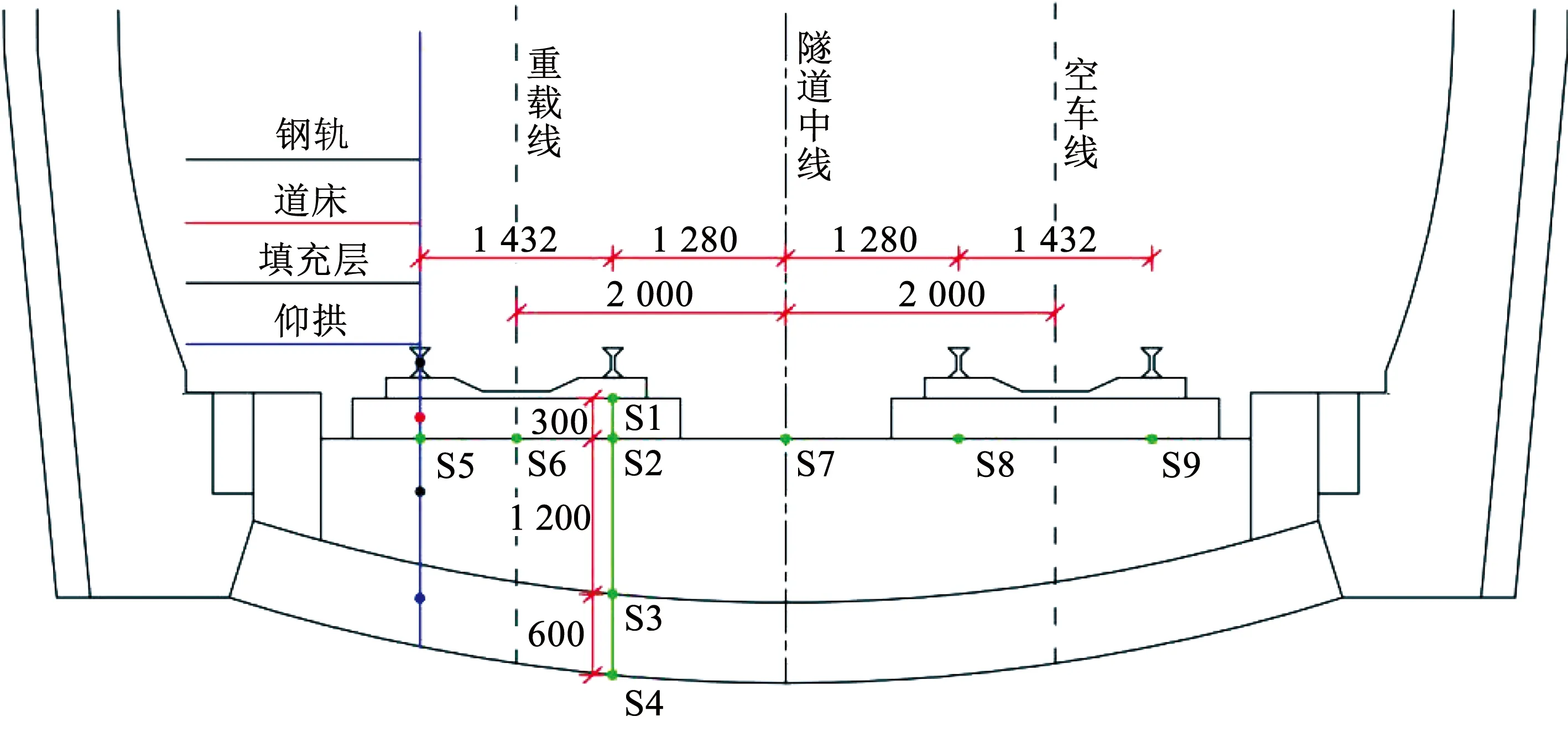
图2 监测点布置(mm)
1.3 实测结果分析
为更清楚观察现场实测竖向动应力时程曲线的规律性,选取前12 s内的时程曲线如图3所示。由图3可得,当列车通过隧道时,各测点竖向动应力分布规律基本一致,且均为压应力。提取测点S1~S9竖向动应力峰值并绘制成如图4所示的变化规律。由图4可知,竖向动应力沿隧道基底竖向呈衰减趋势,测点S1处竖向动应力峰值为150.8 kPa,衰减至S4处为15.7 kPa,衰减率为89.6%。由于受重载列车的影响,隧道左线充填层表面各测点的竖向动应力峰值明显高于右线。左线中心处竖向动应力峰值最大,为105.1 kPa,这是因为列车荷载作用在两条轨道上,振动荷载传递到填充层表面时会引起应力叠加。动荷载在填充层表面呈现以隧道左线中心为轴,向两侧逐渐扩散的规律。
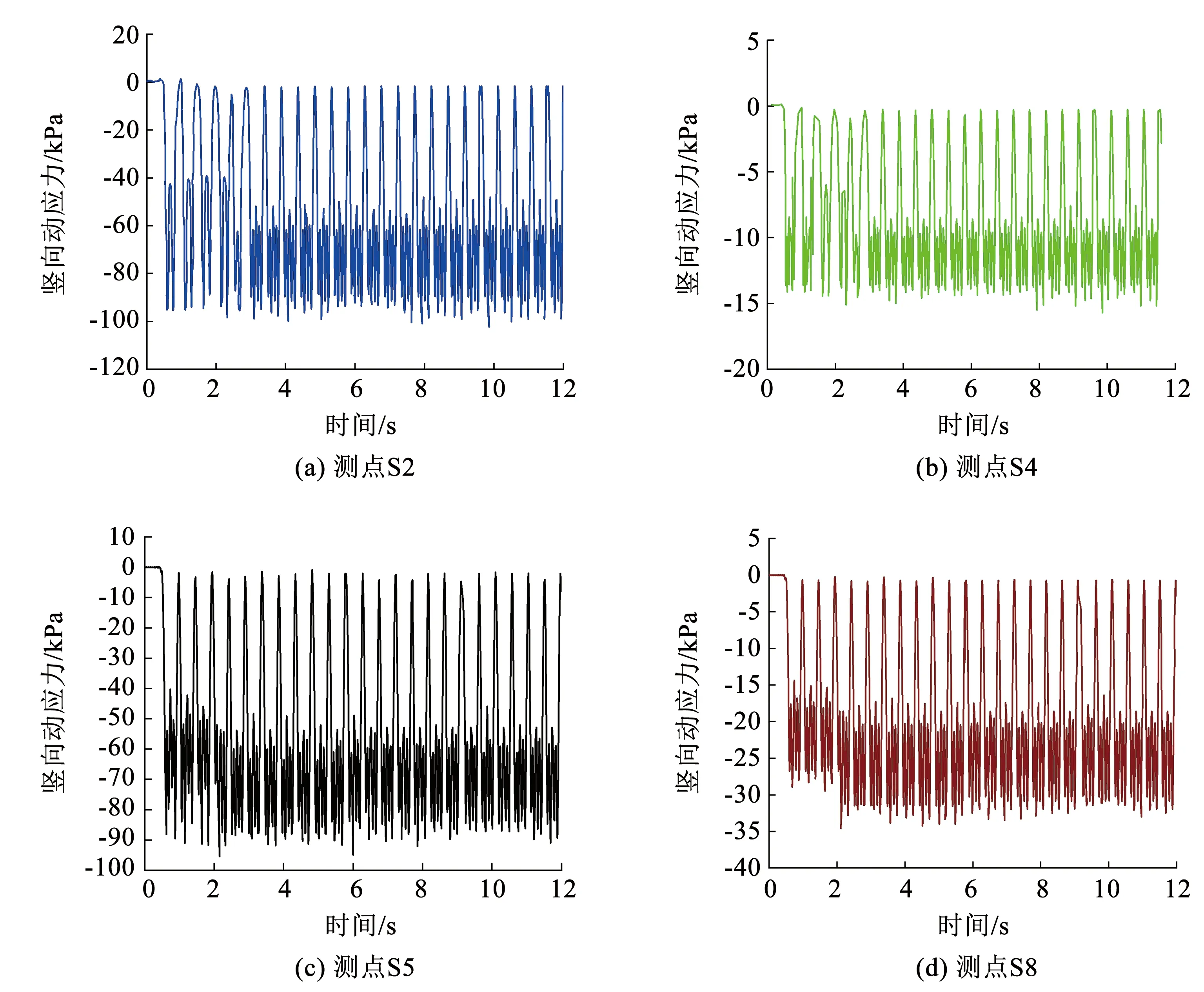
图3 竖向动应力时程曲线
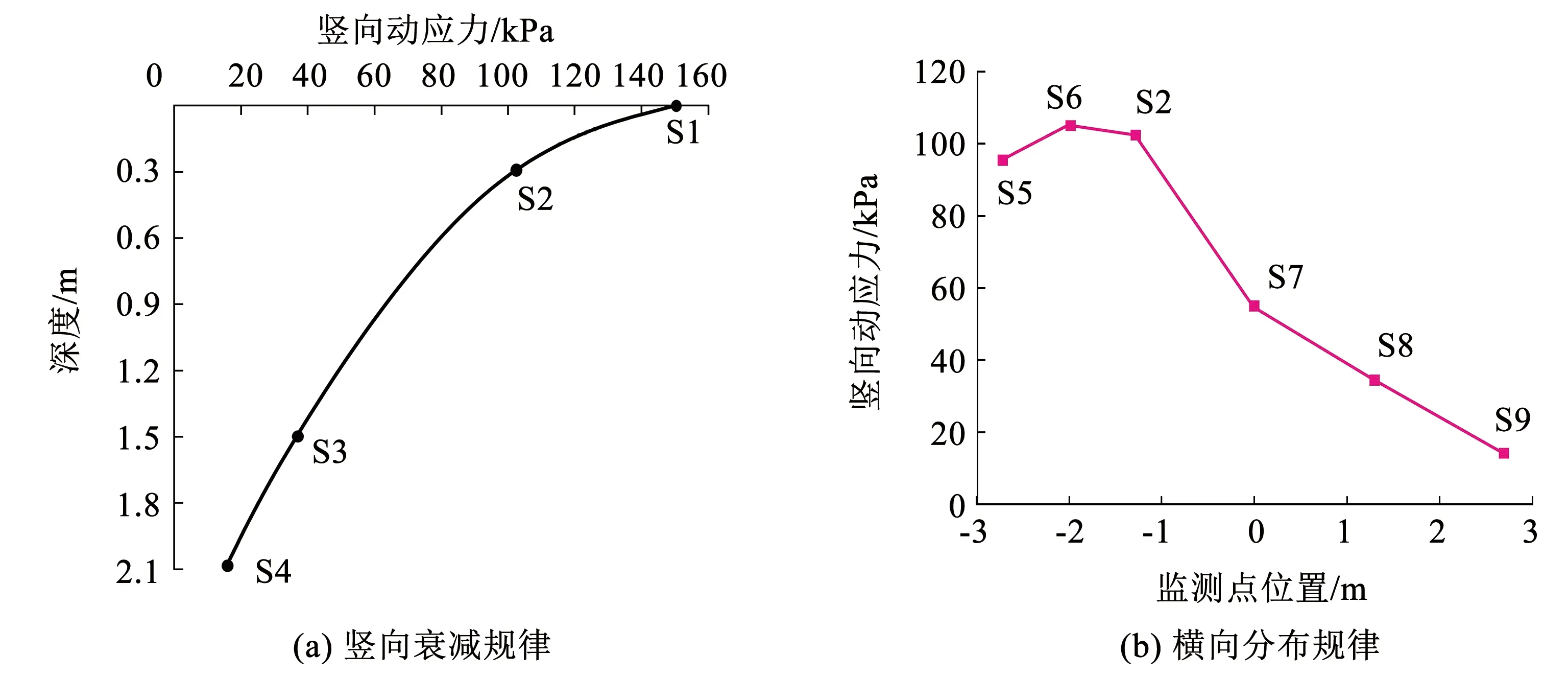
图4 竖向动应力分布规律
2 模型的建立
因现场测试条件的限制,隧道动力响应特性的研究经常用到数值模拟的方法[16-17]。本文采用有限差分软件FLAC3D进行三维数值模拟,建立的数值模型如图5所示,模型沿隧道轴线方向长度取两节重载列车长度约为30 m,宽度自隧道轴线向两侧各取3倍洞径约为30 m,高度自隧道轴线向上取至地表,向下取3倍洞径约为30 m。计算模型整体尺寸为(X方向)60 m×(Y方向)30 m×(Z方向)48 m。本文中隧道结构和围岩均采用实体单元模拟,为了准确描述模型中波的传播,在划分网格时,模型单元的尺寸应小于输入波中最高频率所对应波长的1/10~1/8[18]。

图5 数值计算模型
数值模型的局部放大如图6所示,为对比分析建立脱空形状为椭圆、余弦和矩形的数值模型。
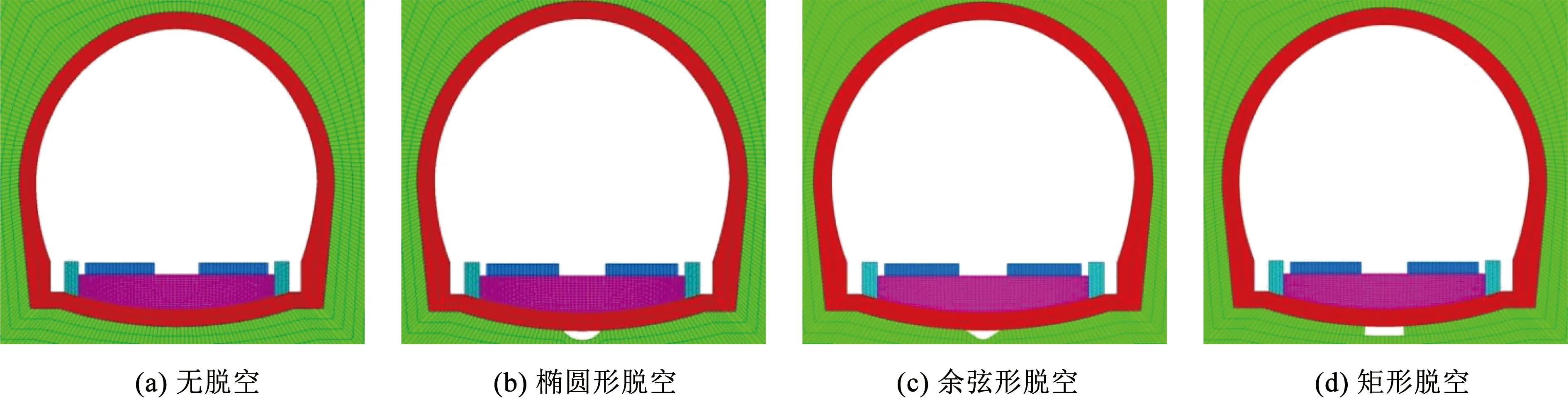
图6 模型局部放大
参考铁路隧道设计规范[19],计算模型中隧道结构及周围地层的物理力学参数见表1。其中,围岩内摩擦角为25°,黏聚力为55 kPa,渗透系数为1.078×10-4cm/s,孔隙度为0.45。围岩在静力计算时采用Mohr-Coulomb模型,动力计算时采用Byrne 模型[20],隧道结构的道床、填充层、仰拱、初支及二衬均采用线弹性模型。静力计算时,模型上表面为自由边界,其余表面均设置法向约束;动力计算时,为减小振动波在结构边界上的反射问题,除模型顶面为自由边界外,模型四周和底部均采用静态边界条件;动力分析中阻尼采用瑞利阻尼。
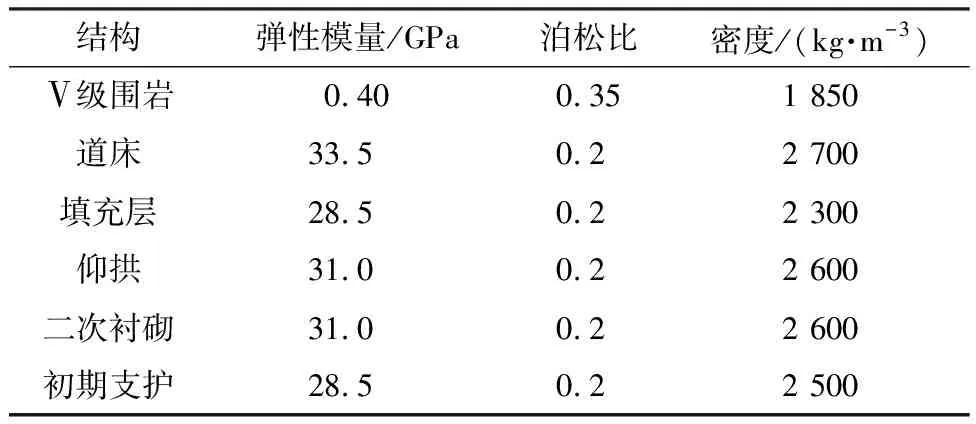
表1 物理力学参数
水-力耦合计算的实现过程为:在进行动力计算之前首先模拟出稳定的渗流场,然后在此基础上进行动力分析。稳定渗流场平衡状态的计算首先关闭力学进程(SET mech off),打开流体进程(SET flow on)进行单渗流计算,建立初始孔压场。而后关闭流体进程,打开力学进程,将土体原先的摩尔-库伦模型替换为Byrne模型并赋予相应的模型参数,最终进行动力与渗流的耦合计算。
2.1 列车动荷载的施加
目前广泛采用由经验公式拟合的激励力函数来模拟列车荷载,该方法既将轮轨力在线路上的移动叠加效应考虑其中,又考虑了钢轨的分散作用以及轨道不平顺等影响因素,可全面探讨列车轴重、车速等因素的影响。激振力函数[21]为
P(t)=k1k2[p0+p1sinω1t+p2sinω2t+p3sinω3t]
(1)
式中:p0为车轮静载;p1、p2、p3均为振动荷载;k1为轮轨作用的叠加系数,取值为1.2~1.7;k2为轮轨作用的分散系数,取值为0.6~0.9。
令列车簧下质量为M0,则相应的列车振动幅值为
(2)
式中:ai为典型矢高;ωi为对应车速下不平顺振动波长的圆频率,分别对应表2中典型值。
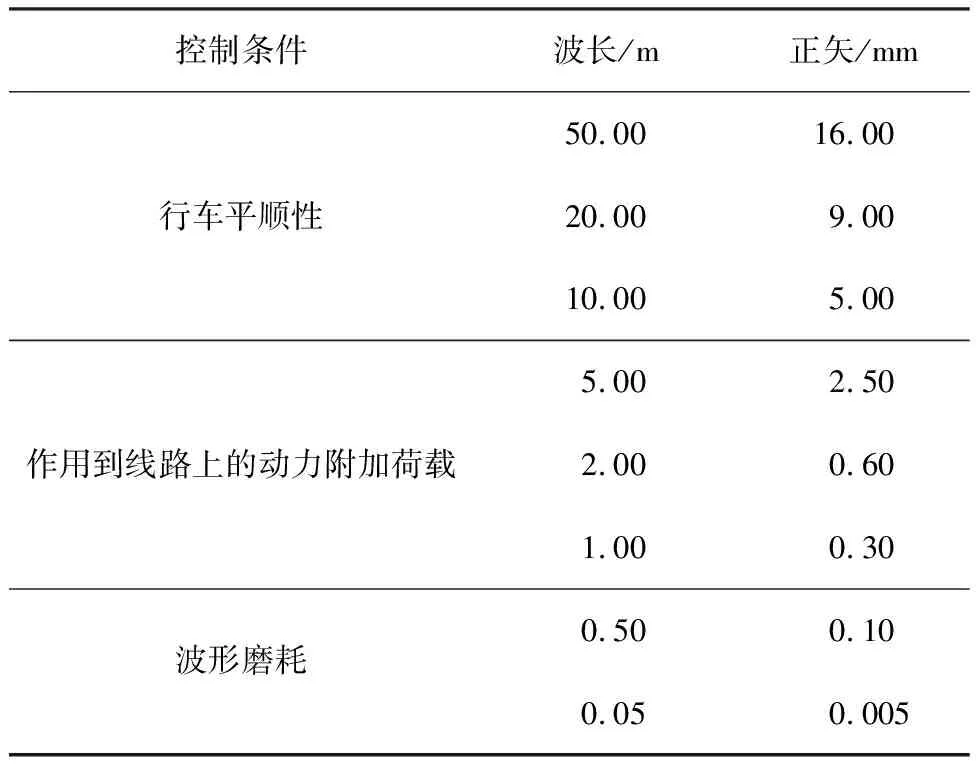
表2 英国轨道几何不平顺管理值[21]
ωi=2πv/Li,i=1,2,3
(3)
式中:v为列车运行速度;Li为典型波长,分别与表2中控制条件的3种情况相对应。
计算列车荷载时,应采用单边静轮重,重载列车的簧下质量M0取1 200 kg,根据式(1)得到27 t轴重下,列车运行速度为80 km/h时的列车荷载时程曲线如图7所示。

图7 列车荷载时程曲线
2.2 模拟工况
根据文献[22-23]的室内试验结果,参考铁路路基底部围岩脱空形状[24],本文将重载铁路隧道基底围岩脱空形状分为图8所示的椭圆、余弦和矩形3种类型。选取A、B、C、D、E点分别代表轨下仰拱上表面、仰拱中心上表面、轨下仰拱下表面、围岩脱空边缘处及仰拱中心下表面作为分析监测点。文献[7]表明,基底围岩脱空高度对结构动力响应影响很小,且高度最大不超过20 cm。因此,本文不考虑脱空高度的影响,高度统一取10 cm,脱空宽度在3种脱空形状下分别取0、0.3、0.6、0.9、1.2、1.5和1.8 m共计21个工况。
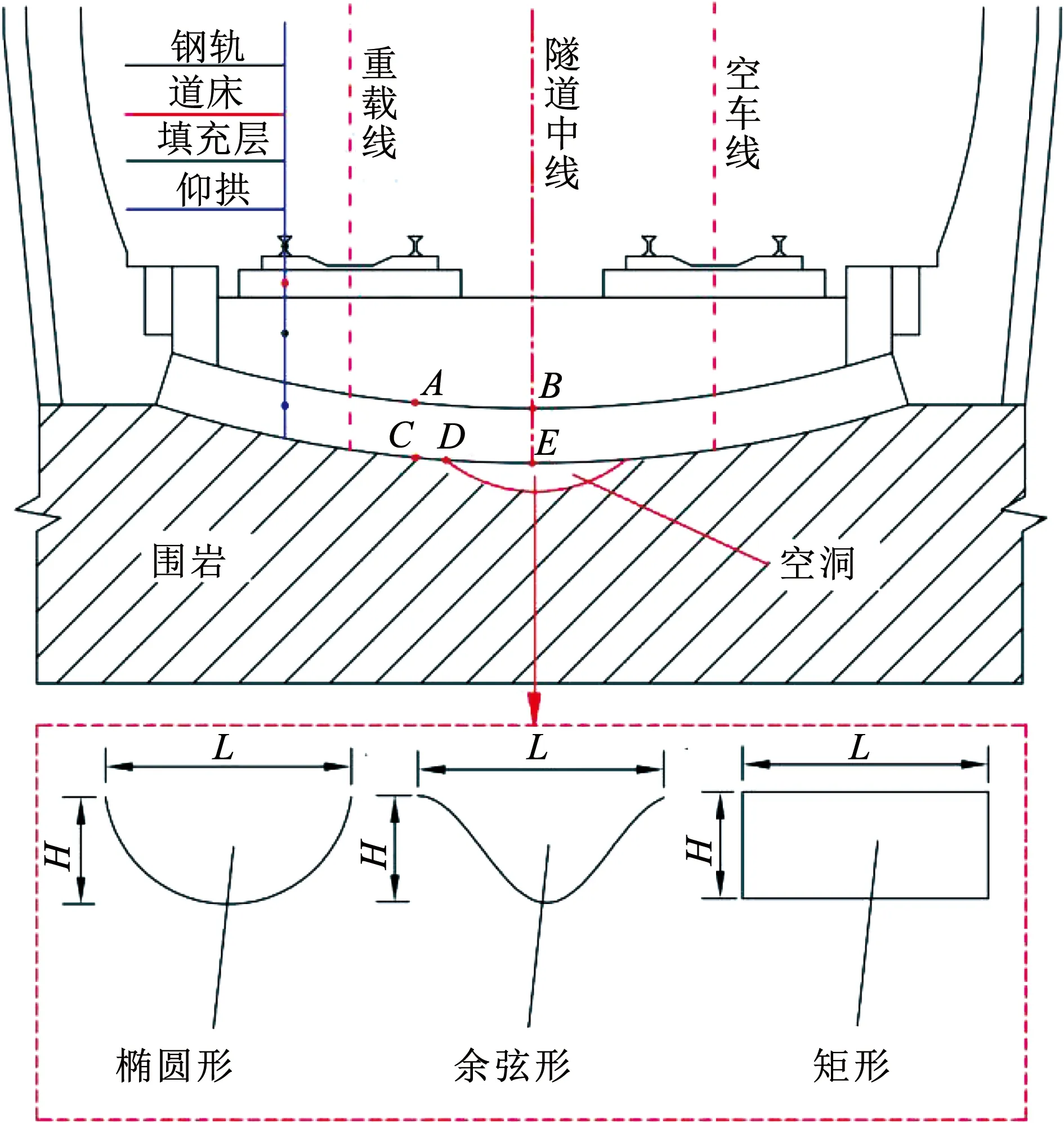
图8 3种基底围岩空洞形状
3 模型的验证
为验证数值模型的可靠性,提取27 t轴重荷载作用下数值模拟的基底测点S1~S9的竖向动应力峰值并绘制成图9所示的曲线对比图。由图9可知,同一工况下,数值计算得到的动应力峰值与现场实测结果相差不大,总体偏差在2%~10%之间。需要说明的是,实测数据与仿真结果存在一定差异,这是由于两者的作用位置和作用方式不同所致。现场试验时,列车直接作用于钢轨表面,动载荷受轨道不平顺值等诸多因素的影响。而数值模拟直接作用于道床表面,列车载荷近似为式(1)。 这也会使两者的动态应力时程曲线不同。但两者的峰值比较接近,且竖向动应力沿基底深度的衰减曲线基本一致(图9(a)),水平分布规律基本一致(图9(b))。这表明本文所采用的数值模型是可靠的,这一观点已在文献[15,25-26]中得到了验证。
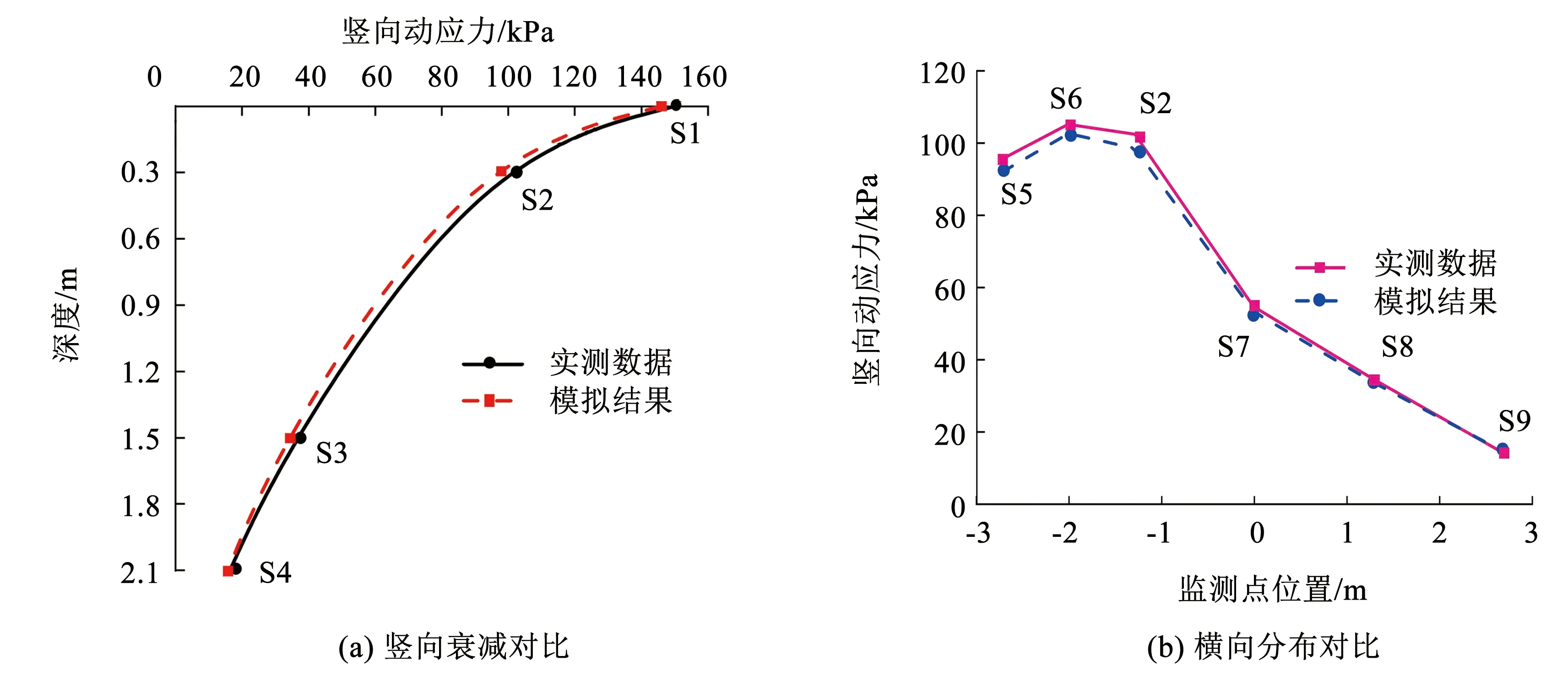
图9 现场试验与数值模拟结果对比
4 结果与分析
4.1 位移响应分析
图10为测点D典型工况的位移时程曲线,位移峰值随脱空宽度的变化规律见图11。由图10可知,在加载瞬间,由于振动荷载的冲击作用,测点位移迅速上升到最大值,随后轻微回弹至某一水平并呈周期性变化。且随着脱空宽度的增加,测点各部位竖向位移的大小和振动幅值均有所增大。由图11可知,脱空形状为椭圆形和矩形时,在脱空宽度为0.9 m时发生突变,随后位移变化加剧;脱空形状为余弦形时,在脱空宽度为1.2 m时发生突变。3种脱空形状下,仰拱上表面测点位移最大处均发生在仰拱中心,脱空形状为椭圆、余弦和矩形时,脱空宽度从0 m增加到1.2 m,位移从0.72 mm分别增加到1.84、1.06、1.92 mm,分别增大了1.12、0.34、1.2 mm,可见,矩形和椭圆形的脱空形状对隧道基底结构的影响更大。

图10 竖向位移时程曲线

图11 竖向位移与脱空宽度关系
4.2 超静孔隙水压力响应分析
图12为点D典型工况的超静孔隙水压力时程曲线,测点超静孔隙水压力峰值随脱空宽度的变化规律见图13。由图12可知,各工况下测点超静孔隙水压力峰值均出现在列车振动荷载作用瞬间(约0.16 s处),随后很快恢复至某一水平(约0.5 s处),并做周期性运动,表现出明显的振动冲击特征。随着脱空宽度的增加,仰拱下表面测点超孔压峰值和振动幅值均有所增大。由图13可知,测点C处超孔压随脱空宽度增加呈指数型增长,测点D处超孔压随脱空宽度增加呈现先缓慢增加,达到某一值后急剧增加的特点。脱空形状为椭圆形和矩形时,测点D处的超孔压在脱空宽度为0.6 m时产生突变,之后变化逐渐加剧;脱空宽度从0 m增加到0.9 m时,最大超孔压由6.2 kPa增加到12.4、12.8 kPa,增幅约为2倍。
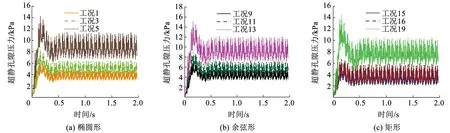
图12 超静孔隙水压力时程曲线
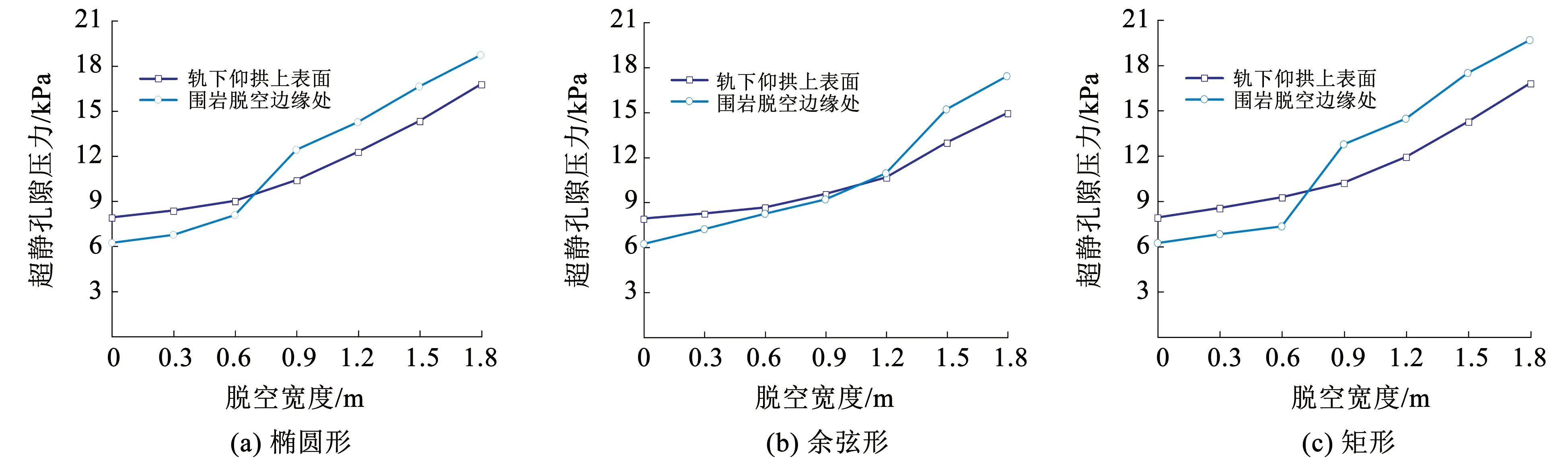
图13 超静孔隙水压力与脱空宽度关系
4.3 动应力响应分析
图14为各测点竖向动应力峰值随脱空宽度的变化规律,由图14可知,轨下仰拱上下表面测点竖向动应力随脱空宽度的增加呈线性变化,其余测点由于处于脱空位置处,在脱空达到一定程度后测点动应力产生突变。整体来看,椭圆形和矩形脱空在脱空宽度达到0.6 m时产生突变,脱空形状为余弦时,在脱空宽度为0.9 m时产生突变。以椭圆形脱空为例,在仰拱上表面,脱空宽度为0~1.2 m时,测点A动应力最大,脱空宽度为1.2~1.8 m时,受基底脱空的直接影响,测点B处动应力最大;仰拱下表面在脱空宽度大于0.9 m后,测点D处动应力最大,这说明测点D可能发生了瞬态冲击和应力集中。在测点D处,脱空宽度从0 m增加到0.9 m时,最大动应力由7.9 kPa增加到22.3 kPa,增幅约2.8倍。

图14 竖向动应力与脱空宽度关系
4.4 不同脱空形状下动力响应对比分析
选取测点D进行不同脱空形状下的动力响应对比如图15所示。由图15可知,椭圆与矩形脱空的动力响应分布规律基本一致,测点竖向位移在脱空宽度为0.9 m时发生突变,测点超静孔隙水压力与竖向动应力在0.6 m时发生突变,这说明与竖向位移响应相比,测点超静孔隙水压力、竖向动应力响应对基底状况更加敏感。随脱空宽度的增加,椭圆形和矩形脱空的动力响应普遍大于余弦形。以脱空宽度为1.8 m为例,无脱空 、椭圆形、余弦形和矩形脱空的最大竖向位移分别为0.3、1.38、0.92、1.6 mm;最大超静孔隙水压力分别为6.2、18.72、17.4、19.68 kPa;最大竖向动应力分别为7.9、38.37、33.86、41.47 kPa。可以看出,采用矩形脱空时,脱空边缘处动力响应最大,与无脱空相比其动力响应增幅达到了5倍,表明该类型脱空对仰拱的应力状态最不利。余弦形脱空在3种脱空形状下动力响应最小。椭圆形脱空的动力响应程度与矩形相差不大,且据现场调研,实际隧道基底脱空中,以椭圆形脱空居多,很难形成矩形脱空。文献[22-23]室内试验结果表明,激振荷载和地下水共同作用下,隧底仰拱围岩脱空多呈椭圆形。这一试验结果与本文所得结论相契合,因此,可以认为,椭圆形脱空是简化的3种类型中较为符合实际的形式。
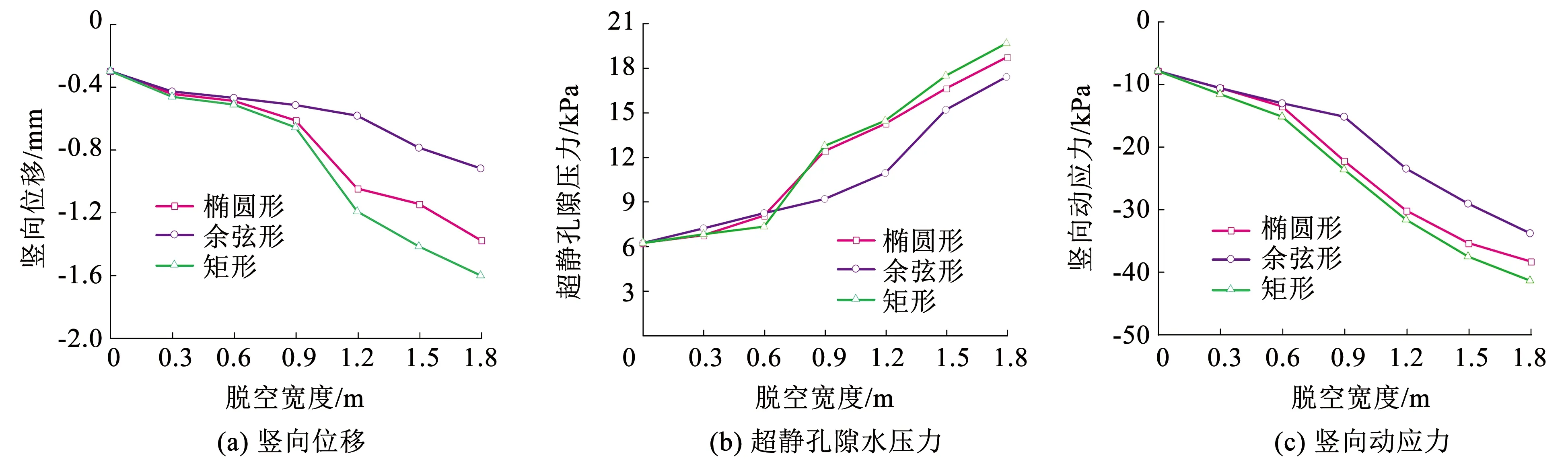
图15 D点(围岩脱空边缘处)不同脱空宽度下的动力响应
4.5 指数分析
图16研究了脱空形状为椭圆形时,不同脱空宽度和列车轴重(25、27、30 t)下D点的动力响应特性。总的来说,随着脱空宽度的增加,25 t和27 t轴重列车荷载下测点动力响应几乎同步逐渐增大,而30 t轴重下则急剧增大。随着列车轴重的提高,基底动力响应也随之增大,列车轴重由25 t增加到27 t时,测点竖向位移、超静孔隙水压力和竖向动应力的增长率分别为8.91%~16.67%、7.23%~19.70%和17.72%~27.74%;列车轴重由27 t增加到30 t时,增长率分别为16.82%~26.92%、18.40%~33.56%和28.31%~46.1%。可以看出,列车轴重的提高及基底脱空宽度的增加对基底动力响应影响巨大,尤其对基底竖向动应力的影响,最大增幅达到了46.1%。根据图中测点动力响应发生突变时的位置,建议重载铁路隧道富水基底脱空宽度达到0.6 m时,立即采取相应措施对隧道基底脱空进行整治,防止基底病害的进一步扩大,保证重载铁路隧道的运营安全。
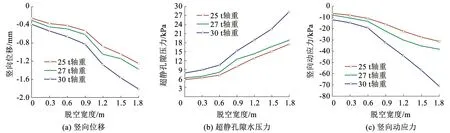
图16 不同脱空宽度和列车轴重下测点D的动力响应
5 结 论
1)水-力耦合作用下,基底仰拱与围岩界面会发生恶化,形成脱空,随着细粒损失的逐步发展,隧道基底围岩脱空可简化为椭圆形、余弦形、矩形3种类型。
2)从动力响应随围岩脱空宽度变化的分布特征及结合现场实际情况来看,建议采用简化的椭圆形状来描述隧底围岩脱空,该脱空下隧底动力响应是无脱空情况下的4.2倍。
3)重载列车轴重的提高对基底动力响应影响巨大,尤其是当列车轴重由27 t提升到30 t时,基底动力响应会加速增大,最大增幅达到了46.1%。
4)在脱空宽度大于0.6 m的情况下,超静孔隙水压力和竖向动应力峰值发生突变急剧增大,富水地层重载铁路隧道基底围岩脱空宽度达到0.6 m时,应立即采取相应措施对隧道底部围岩脱空进行整治。
