基于贪心算法的自动路径规划送药小车

徐小小 周启银 娄成龙 夏 宇

（贵州师范大学物理与电子科学学院，贵州 贵阳 550025）

0 引言

随着无人驾驶技术的不断创新发展，小车自动规划路径成为当今社会的热点。为了实现医院无接触配送药品，该文进行了以无人小车为主的精细化、智慧化送药服务[1]的研究。

黄汇华等[2]采用K210、OpenMV 和STM32 共同组成的智能送药小车能按规定的路线完成送药任务，但是在送药之前需要布置小车轨道。闭世管等[3]基于MSP-423E401Y 单片机、LV8548MC 芯片、OpenMV 识别模块和NRF24L01 通信模块实现不同药房的送药、取药功能。万瑞丰[4]基于OpenArt和TC377 设计的送药小车虽然降低了小车送药的操作复杂度，但是在寻迹过程中的识别受光线的影响较大。肖光亚[5]基于Arduino 的智能送药小车通过识别地面的安置路线自动避障，以实现往返送药的功能。

在总结国内学者对智能送药小车相关研究的基础上，针对送药小车在二维平面下如何规划出最优路径，以提高送药效率，该文提出了一种基于贪心算法的改进RRT 算法。该算法可以建立医院内部的坐标图，并在获取目标位置的坐标点后，根据医院内部各个部门的坐标位置动态规划出1 条最优的路径。

1 贪心算法和动态规划法

贪心算法是将一个问题分成多个子问题，自顶向下以循环递归的方式快速地进行贪心选择，从而求出子问题的最优解，进而简化数学模型的规模[6]，并把迭代求解出的局部问题最优解集合为整个问题的最终解[7]。贪心算法常运用于子问题具有最优解的问题中，其算法流程为建立能描述问题的数学模型、把问题分成多个子问题、对子问题进行求解、获得子问题的最优解以及将集合子问题的最优解作为整个问题的解。问题的求解关键是贪心策略，当选择贪心策略时须注意策略应具有无后效性，即当前状态与前一个状态没有统计学意义，单独节点的问题单独求解，第一次选择不需要前一个时刻子问题的解。无后效性是贪心算法区别于动态规划法的本质特点。

动态规划法是自底向上地求解子问题的解，这是一种与前一个状态有关联的求解方法，当第一次选择时，需要求解前一个时刻子问题的解，只有求解出前一个时刻子问题的解才能求解下一个子问题。该算法具有重叠子问题的性质，在循环递归时会解决相同的问题，但是不会一直生成新的子问题。

2 贪心算法

2.1 贪心算法的基本步骤

贪心算法的求解过程为读入问题、制定贪心策略、问题排序以及处理问题[8]。贪心算法从问题的初始解出发，不断向目标点逼近，每步都是不可回溯的决策，根据贪心选择的性质，归并一系列的局部最优解，以得到所求问题的解。该算法的核心思想是待求解问题的最优解依赖于子问题的最优解。该思想缩小了解决问题需要考虑的范围，将全局变成局部，有利于降低算法的复杂度。

2.2 贪心算法的适用性

贪心算法具有最优子结构的性质，即整体的解取决于局部子问题的解。该特性使贪心算法的适用范围受到限制，即只有局部子问题最优解能决定全局最优解的情况才适用贪心算法。贪心算法的可信度可以通过数学方法证明，通过该算法能够得到解决整个问题趋于最优的解。

2.3 贪心算法实例——Prim 算法、Kruskal 算法

Prim 算法和Kruskal 算法是贪心算法中常用的算法，2 种算法的运行机制不同，因此其执行过程也存在差异，但这2 种算法都是求连通网的最小生成树，可以将每条边线逐步添加到没有任何边线的状态的树中。

2.3.1 Prim 算法

文献[9]中，该算法是从任一根节点出发，利用贪心算法把离顶点最近的顶点添加到生成树，不断扩大所含顶点的个数，当最后一个节点被添加到生成树时结束。与Kruskal 算法相比，该算法不受网络图稠密的影响。Prim 算法随机选取1 个顶点，在图1 中选取A为初始根节点，计算其与无向图中的其他节点的距离，选取最小的边添加到生成树，循环上述流程，将节点添加到生成树，直到终点被添加到生成树。Prim 算法在无向图中的执行过程如图1 所示。由图1 可知，Prim 算法得到的最小生成树是权值最小、有n个顶点且有n-1 条边的带权无向完全图。该算法是对所有节点进行直接搜索的，涉及多次迭代。

图1 Prim 算法执行图

图1 以A点为起点，利用Prim 算法得到的最小生成树的每条边上的数值为两点之间的权重，算法通过判断权重生成“ABDGEC”的扩展树，其中不包括F点，比较连接F点的权重可以得到G指向F的扩展树。

2.3.2 Kruskal 算法

Kruskal 算法可以选择任意的起点，主要应用在互斥集合数据结构中。该算法的贪心策略是将所有节点与当前节点的权值进行比较，第一条边是最小权值的边线，再在其余边线中任意选取一条边线放在已有的边线中，按照此方法循环取出边线，最后得到最小生成树。

Kruskal 算法执行图如图 2 所示，选择D点作为起点，对边线的权值进行排序，将权值最小的边线添加到最小生成树。橙色的粗线代表被添加到生成树的边线，即将图2 中DGEC先放入生成树，再将A、F的边线进行排序，把B到A、D到F加入树中。该算法当将边线添加到最小生成树时还须注意其是否会与生成树中其他边线产生回路，并将会产生回路的边线删除。要判断是否产生回路，需要对生成树进行深度优先搜索，判断逆向边是否存在。按照上述方式将所有的边线添加到生成树。

图2 Kruskal 算法执行图

由上述原理介绍可知，网络图边线数量对Kruskal 算法的影响较大。

对比Kruskal 算法与Prim 算法建立生成树的方法可知，Kruskal 算法是先对权重进行排序，选取最小的权重添加到生成树；Prim 算法则是直接对其他的节点进行循环查找，搜索权值最小的节点放入最小生成树。因此当边线繁杂时选用Prim算法，如果考虑时间复杂度，那么Kruskal 算法的效率比Prim算法效率高。

3 二维坐标系下贪心算法结合动态规划规划最优路径

3.1 RRT 算法

RRT 算法是基于随机采样的快速扩展树，通过与障碍物产生碰撞检测是否将该节点添加到扩展树，多次循环检测直到到达目标点，再从目标点回溯到起始点，就可以找到路径。与Dijkstra 算法、粒子群优化算法和人工势场法相比，该算法的搜索能力强、参数少且搜索路径的速度快，适用于高维复杂环境下的路径优化。在扩展生成树的过程中，扩展的节点是随机采样的，因此其搜索的路径只能找到两点之间的路径，并不能得到最优路径并且冗余节点的计算量大、规划时间响应时间太长，容易导致路径规划失败。

3.2 贪心算法融合改进的RRT 算法规划流程

为了解决传统的RRT 算法带来的路径规划非最优、搜索速度慢的问题，该文引入贪心算法中的Kruskal 算法选择每个子问题的最优解并舍弃其他解，以减少冗余点的计算量。RRT算法路径规划的优化主要进行以下5 个步骤：1）随机树初始化。2）进行随机采样。3）扩展节点。4）终点停止扩展。5）处理冗余点。

3.2.1 随机树初始化

当该算法在读取坐标系时，以当前位置为快速扩展树的搜索起点，以接收到的目的地坐标点为快速扩展树的终点。随机树的初始化包括根节点和带阈值的终点。

3.2.2 进行随机采样

随机树的扩展采用随机采样检测节点是否存在碰撞，从而判断该点是否存在障碍物。利用欧氏距离计算空间中两点的距离，二维环境下的欧氏距离、三维坐标系上的欧式距离如公式（1）、公式（2）所示。

式中：（x1，y1）为直线一侧端点的坐标点；（x2，y2）为直线另一侧端点的坐标点；z1、z2为2 个点在z坐标轴上的坐标。

可以将公式（2）推广到三维坐标中，还可以将公式（1）推广到n维坐标系上。在对计算的距离进行排序后，选择距离最短的节点进行碰撞检测（判断2 个节点之间是否存在障碍物）。如果无障碍物发生碰撞，那么将该节点添加到快速扩展树；如果该节点发生碰撞事件，算法判断该点存在障碍物，那么重新生成随机点，再循环检测欧氏距离的计算和判断。

3.2.3 扩展节点

节点的扩展须基于上一步骤检测碰撞事件，将没有发生碰撞事件的节点添加到随机树，以扩展随机树。

3.2.4 终点停止扩展

随机树初始化时需要设置一个带阈值的终点。当扩展树的节点与终点的欧式距离小于设置的阈值时，程序判断该节点是终点，停止随机树的扩展。完成上述步骤后就可以得到1条从起点到终点的路径。

3.2.5 处理冗余点

冗余点删除前后对比图如图3 所示。由图3 可以得到冗余点处理表，见表 1。

图3 冗余点删除前后对比

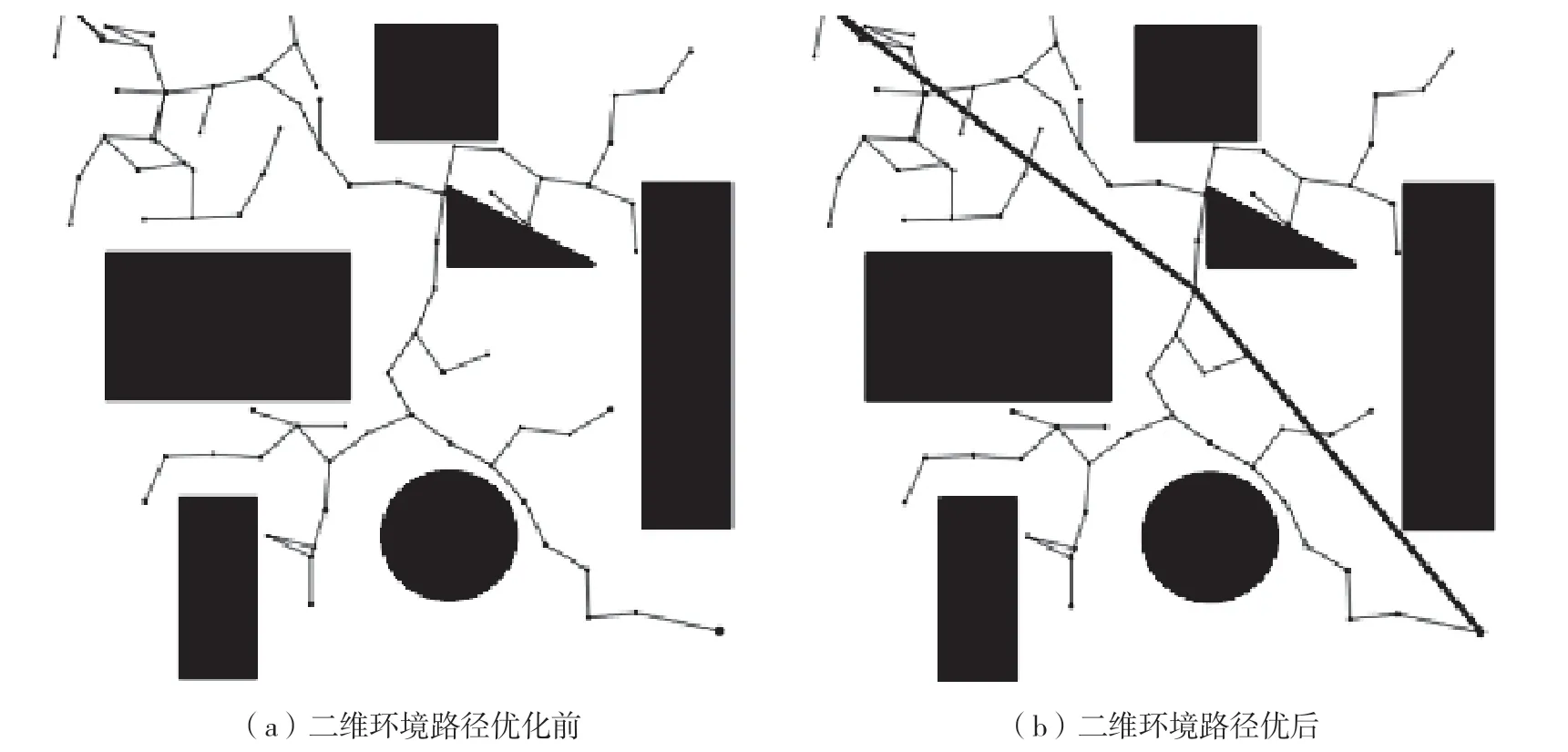
图4 二维环境路径优化对比图

贪心算法结合改进的RRT 算法在二维环境下的路径优化对比图如图 4 所示。

4 结语

针对传统送药小车按轨道寻径存在灵活性差、工作效率低和适用范围容易被限制等问题，该文提出将Kruskal 算法与RRT 算法结合，建立医院内部的坐标图，自动规划最优路径，以完成送药任务。该算法使送药小车能够灵活选择医院的各个位置，不再局限于只在轨道上运动，且该算法不用识别地面上的轨道，外界的亮度就无法对其产生影响。利用贪心算法提取最优解，可以减少路径冗余点的计算量，结合改进的RRT 算法能够快速找到最优路径，提高送药小车的工作效率。但是该文研究算法的试验背景是在道路上没有行人的场所，如果要将该算法投入使用，还需要实现送药小车的实时避障功能。将最优路径算法结合实时避障算法，最终使送药小车能够灵活避开行人，快速完成送药任务。

表1 冗余点处理表