基于混沌反馈乌燕鸥优化算法的随机配置网络参数优化

严爱军, 于 小

(1.北京工业大学信息学部, 北京 100124; 2.数字社区教育部工程研究中心, 北京 100124; 3.城市轨道交通北京实验室, 北京 100124)

随着工业信息化技术的不断发展和数据规模的不断增加,一些经典神经网络算法模型的学习性能不太理想,难以满足应用需求。2017年,由Wang等[1]提出的随机配置网络(stochastic configuration network, SCN)可在一个可调区间内随机分配隐含层参数,并引入监督机制加以约束,具有万能逼近性质。SCN已被应用于大数据处理[2]、机器人抓取识别[3]、工业过程建模[4-5]等领域,在解决大规模数据回归和分类问题上具有良好的性能,因此,对SCN的建模研究得到了广泛关注[6-9]。

值得注意的是,SCN隐含层参数选择的随机性会影响SCN算法的求解性能,因此,针对SCN算法参数的优化问题具有现实意义。目前,对神经网络参数优化的方法主要有网格搜索[10]、随机搜索[11]和元启发式算法[12]等。网格搜索方法是对参数值的一种穷举搜索,通过遍历给定的参数集合实现优化,这种优化方法十分耗时。随机搜索方法通过随机抽取一定范围内的参数进行验证,在一定程度上提高了搜索效率,而且易于实现,但这种方法的优化效果依赖于随机概率的选择。为了避免这2种参数优化方法的缺陷,将元启发式算法应用于神经网络的参数优化更为常见。元启发式算法具有灵活、易于实现的特点,可以通过迭代的方式寻找最优参数[13],主要分为单解算法和多解算法。其中,单解算法从某个候选解开始搜索,然后在迭代过程中改进此候选解,比如模拟退火算法[14]等。目前,也有研究将单解算法应用于SCN的隐含层参数优化,比如:文献[15]采用天牛须算法来优化隐含层中尺度因子参数的选择,提升了SCN的求解精度。单解算法的求解速度虽然较快,但单个候选解对整个解空间的探索过低,容易陷入局部最优。多解算法可以通过多个候选解共享搜索空间,相较于单解算法有更强的探索能力。多解算法又可分为进化算法和群体智能算法。进化算法有遗传算法[16]、差分进化算法[17]、回溯搜索算法[18]等。这类算法通过模拟大自然的生物进化过程对参数进行优化,具有灵活、运行方便等优点,但普遍存在收敛速度较慢且容易陷入局部最优的缺陷。群体智能算法通过模拟物种的社会行为,凭借其易于实现、保留最优解、参数调整少的特点,已经广泛应用于神经网络的参数优化,比如蚁群算法[19]、鲸鱼优化算法(whale optimization algorithm,WOA)[20]、混沌麻雀算法[21]等。文献[21]采用混沌麻雀算法对SCN隐含层中的正则化参数和尺度因子参数进行优化,实验结果证明,该方法可以有效提高SCN的训练效率和回归精度,但麻雀算法需要预设的参数过多,实际训练可能会花费大量的时间。综上,虽然不同的优化方法对神经网络参数优化均取得了一定的应用成效,但方法的收敛性、计算效率等仍须提高。

乌燕鸥优化算法(sooty tern optimization algorithm, STOA)[22]具有预设参数少、寻优精度高等特点,但该算法存在局部搜索能力弱、收敛速度慢的缺点。针对SCN隐含层参数的优化问题,本文将STOA算法进行改进,并用于SCN的参数优化。首先,通过Tent映射[23]生成初始种群,以解决初始种群在解空间分布不均匀的问题;然后,采用线性因子调节策略来平衡算法的全局搜索能力和局部搜索能力;最后,采用劣势种群反馈原则来增加算法在整个迭代过程的局部搜索能力,从而提出了一种混沌反馈乌燕鸥优化算法(chaotic feedback sooty tern optimization algorithm, CFSTOA),极值问题的求解表明该算法的收敛性能得以提升。以CFSTOA方法为基础,对SCN隐含层中的正则化参数和尺度因子参数进行迭代优化,通过实验验证了CFSTOA优化SCN隐含层参数的有效性。

1 相关研究

1.1 SCN

SCN是一种随机权神经网络,类似于前馈神经网络,包含输入层、隐含层、输出层,它通过监督机制随机分配隐含层参数,并用最小二乘法求解隐含层的输出权重,保证所建立的模型具有万能逼近性质,该网络的配置过程详见文献[1]。

在构建SCN的过程中,输入层节点的个数与输出层节点的个数分别对应训练输入和输出特征的维数,而隐含层节点的个数会随着构建的过程逐步增加,节点增加的条件是当前输出误差大于容许误差。当增加隐含层节点后,构建一个候选层以确定新增节点的权重和偏差,候选层节点的权重和偏差会随机初始化,然后,通过利用特有的监督机制计算不等式约束选出候选层节点中最佳的权重和偏差,并分配给新增的节点。最后,根据此时的隐含层节点输出和输出向量通过最小二乘法计算得到输出层权重。

在整个构建过程中,候选层节点的权重和偏差初始化取决于尺度因子λ,而在监督机制中计算不等式约束会取决于正则化参数r,因此,隐含层节点的输入权重和偏差会受λ和r的影响[21]。然而,这2个参数会在构建SCN前给出2组数据,这就会造成在构建过程中由于参数的选择而消耗过多的时间,进而影响SCN的效率,而且针对不同的问题,预设的2组数据可能无法得到最优参数,从而影响SCN的预测精度。

1.2 STOA

根据文献[22]可知, STOA模拟了乌燕鸥在自然界中觅食的行为,包括迁徙(全局搜索)与攻击(局部搜索)。迁徙即乌燕鸥为了寻找最丰富的食物来源而进行季节性的移动。在迁徙的过程中乌燕鸥会攻击海面上的猎物,具体算法描述及其问题分析如下。

1.2.1 迁徙行为

迁徙行为,也就是探索部分,主要分为3个部分:避免碰撞、聚集和更新。迁移行为通过更新当前最佳乌燕鸥的位置来指导其他乌燕鸥进行位置更新。

1) 避免碰撞。通过附加变量产生不同的位置,避免乌燕鸥在迁徙过程中相互发生碰撞,计算公式为

Cst=SA×Xst(z)

(1)

式中:Cst表示乌燕鸥个体与其他乌燕鸥不发生碰撞时应处于的位置;Xst表示乌燕鸥当前位置;z表示当前迭代次数;SA代表一个避免碰撞的变量因素,用来计算避免碰撞后的位置,约束条件为

(2)

式中:Cf是用来调整SA的控制变量;zmax表示最大迭代次数。一般Cf的值设置为2,因此,SA从2～0线性递减。

2) 聚集。聚集是指在避免碰撞后,乌燕鸥都会向最优个体靠拢,其数学表达式为

Mst=CB×(Xbst(z)-Xst(z))

(3)

式中:Mst表示在不同位置的Xst向最优位置Xbst移动的过程;CB是一个平衡探索与开发的随机变量,按照

CB=0.5×Rand

(4)

变化。式中Rand是0～1的随机数。

3) 更新。乌燕鸥个体按照式(1)中的位置Cst和式(3)中的移动过程Mst更新自己的位置,表达式为

Dst=Cst+Mst

(5)

式中Dst代表当前位置与最优位置之间的距离。

1.2.2 攻击行为

在迁徙行为过程中,乌燕鸥通过翅膀提高飞行高度,同时,不断调整自身的速度和飞行角度以攻击猎物,它们在空中的盘旋行为可以定义为

x′=Radius×sini

(6)

y′=Radius×cosi

(7)

z′=Radius×i

(8)

Radius=u×ekv

(9)

式中:x′、y′、z′分别为空间坐标系上的3个分量;Radius为每个螺旋的半径;i为[0, 2π]中的变量;u和v是定义螺旋形状的常数,一般均取1;e是自然对数的底;k为比例常数。攻击猎物后的新位置的计算公式为

Xst(z)=Dst×(x′+y′+z′)×Xbst(z)

(10)

1.2.3 问题分析

从STOA的实现过程可看出,虽然算法具有易于实现、参数简单的特点,但以下一些问题的存在限制了寻优能力的提升。

1) 初始种群的生成。与其他群体智能算法类似,STOA在求解优化问题时的初始种群是随机生成的,在解空间中可能分布不够均匀,多样性较差,这会影响算法的收敛精度与收敛速度。

2) 随机变量的取值。式(4)中的随机变量CB在一个常量范围内取随机值,这就会导致在迭代前期聚集范围较小,种群不能分布到整个搜索空间,使全局搜索比较费时,而在迭代中后期聚集范围过大,导致乌燕鸥不能快速聚集向最优解,无法快速收敛。

3) 全局搜索和局部搜索不平衡。STOA属于全局优化算法[22],因为式(10)所示的位置更新机制包括了迁徙行为(全局搜索),寻优方式主要依靠算法的迁徙行为,所以算法的局部搜索能力较弱,导致收敛精度较低。

2 基于CFSTOA的SCN参数优化

在SCN模型中,r和λ会在预设范围内选择,这极其影响SCN的效率和精度,因此,需要预先优化确定这2个参数值,思路是:首先,根据STOA存在的3个问题提出改进策略,并实现算法;然后,将改进后的STOA应用于SCN隐含层中的r和λ参数优化,由此构建出SCN。

2.1 STOA的改进

关于STOA存在的3个问题,提出的改进策略包括:第一,利用Tent映射初始化种群位置,改变STOA随机生成种群位置的方式以提高初始解的质量;第二,利用式(2)中的线性因子SA来调节式(4)中随机变量CB的取值,在前期扩大聚集范围,提高算法全局搜索速度,在中后期缩小聚集范围,提高算法局部搜索速度;第三,采用劣势种群反馈原则,增强算法在整个搜索过程中种群的多样性,进一步增强算法的局部搜索能力,提高算法的搜索精度。

2.1.1 混沌初始化策略

初始种群的好坏影响着算法的求解精度和收敛速度,多样性较好的初始种群对提升算法性能很有帮助[24]。然而,STOA算法在求解问题时通常采用随机方法产生初始种群,可能使得初始种群分布不均,导致初始种群多样性较差。此外,由于对优化问题的全局最优解没有任何先验知识,应尽可能使种群均匀分布在搜索空间。为了增强种群的多样性,并提高求解效率,对STOA算法采用混沌初始化策略,利用混沌变量的随机性、遍历性和规律性特征,产生多样性较好的混沌初始种群。

Tent映射[23]是一种常见的混沌映射。假设种群数量为K,Tent映射在D维欧氏空间中生成混沌序列y={yd,d=1, 2, …,D},yd={yid,i=1, 2, …,K},Tent映射函数表达式为

(11)

式中:yid为第d个映射序列在第i行上的分量;a为控制参数,取值范围为0～1.0。

当a=0.5时,Tent映射具有最典型的形式(如图1所示),生成的混沌序列可以均匀地分布在0～1.0,并且不呈现周期性,可以得出通过混沌序列生成的种群会比随机生成的种群具有更高的多样性。因此,本文的Tent映射的公式为

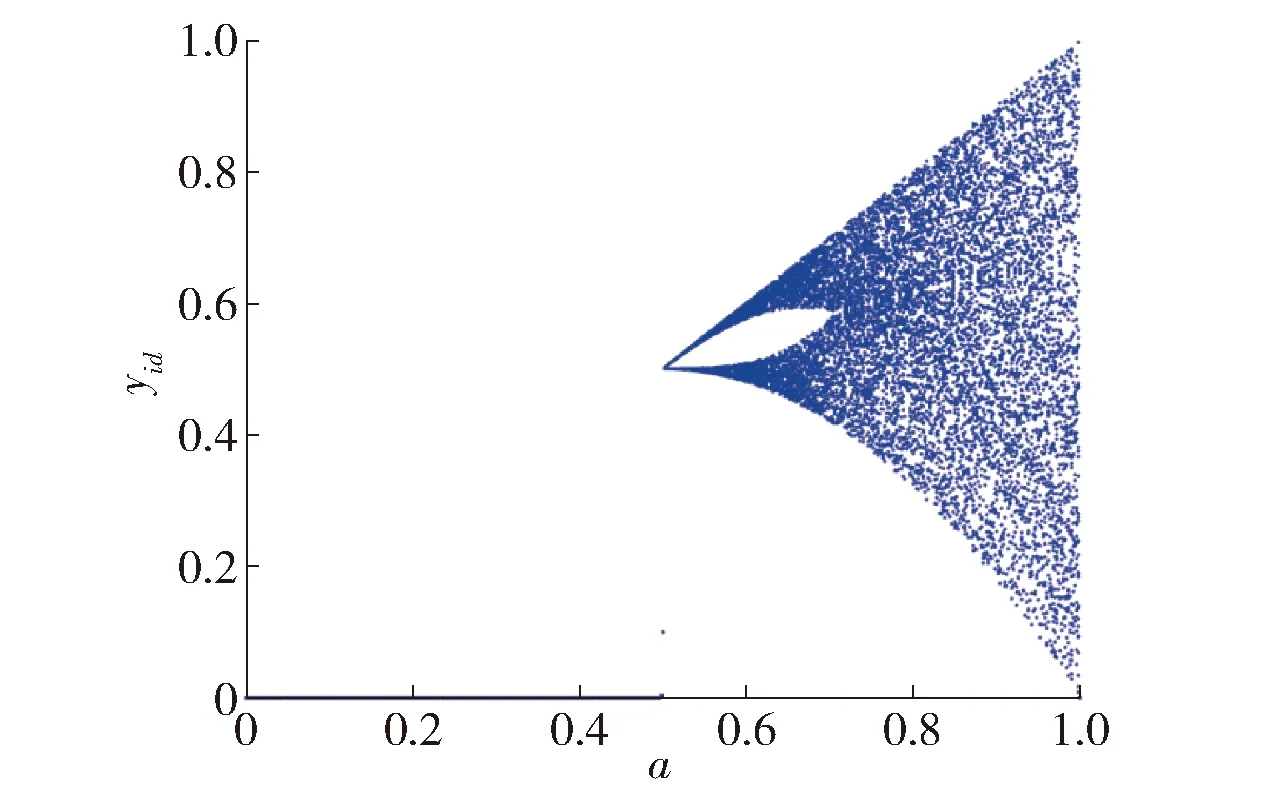
图1 Tent映射分叉Fig.1 Feigenbaum bifurcation of Tent mapping

(12)

将混沌序列映射到解空间中,得到种群X={Xi,i=1, 2, …,K},Xi={Xid,d=1, 2, …,D},种群个体Xid表示为

Xid=Lb+yid×(Ub-Lb)

(13)

式中:Xid为第i个种群个体在第d维上的分量;Ub和Lb分别为Xid的搜索上下界。

2.1.2 线性因子调节策略

在STOA中,CB是一个平衡探索与开发的随机变量,用于控制算法中的聚集行为,即乌燕鸥个体向最优个体靠近,较大的CB会扩大整个种群相较于最优个体之间的距离,有利于全局搜索,而较小的CB会缩短距离,有利于局部搜索。通常情况下,在优化的早期阶段应该探索整个搜索空间,也就是应该使种群尽可能分散在整个搜索空间中,STOA在整个迭代过程中CB是0～0.5的随机数,不利于算法在迭代前期的全局搜索以及在迭代后期的局部搜索。基准数据集的实验结果表明,在大多数数据集尤其是单峰函数中,算法在迭代前期一直没有进行收敛。为了解决算法前期收敛速度慢的问题,这里采用式(2)中的SA优化CB,SA由2～0线性递减,改进后的CB公式为

(14)

改进后的CB从1开始非线性递减,在迭代前期扩大种群个体与最优个体的距离,使算法前期的全局搜索能力增加,解决算法前期收敛速度慢的问题,同时,会因为SA在迭代后期逐渐缩小而减小聚集范围,从而使算法主要进行局部搜索,加快收敛速度。

2.1.3 劣势种群反馈原则

在STOA算法中,乌燕鸥只通过式(10)来更新所在位置,主要依靠迁徙行为进行寻优,局部搜索能力较弱。许多群体智能算法对提高局部搜索能力进行了研究,比如文献[25]中蝠鲼觅食优化算法利用翻滚觅食行为使种群中的每个个体都以最优个体为支点移动到对称位置之间的任何位置,以此来增强算法的局部搜索能力,提高算法的寻优精度。根据这一思想,对STOA采取了类似的处理,通过设置一个比例因子,将种群按照适应度值分为优势种群和劣势种群,优势种群仍然采用式(10)的位置更新公式,劣势种群中的个体按照类似于蝠鲼觅食优化算法的翻滚觅食行为,与最优个体有目的地进行反馈交流。通过反馈信息交流,距离猎物较远的乌燕鸥可以快速移动到猎物附近,添加反馈行为后的数学描述为

Xwst_new(z)=Xwst(z)+2×CB×(Xbst(z)-Xwst(z))

(15)

(16)

(17)

式中:Xwst_new(z)表示劣势个体经过反馈后的新位置;Xwst(z)表示劣势种群中个体的位置;Xbst(z)表示当前最佳个体的位置;Xnew(z)表示适应度值较低的位置;fit(·)表示适应度函数;Xst(z)表示更新后的新位置;i=1, 2, …,K;ρ表示划分优势种群与劣势种群的比例因子。

起初,当CB∈(0.5, 1.0)时,劣势个体会向优势个体靠拢或者移动到最优个体的对立随机位置,在前期随机对立的飞行可以探索未知位置,提高种群多样性;当CB∈(0, 0.5)时,劣势个体便只向优势个体靠拢,在后期只进行局部搜索,以增强算法的局部搜索能力。

2.1.4 算法伪代码

综上所述,采用混沌初始化策略、线性因子调节策略和劣势种群反馈原则得到了一种CFSTOA算法,见算法1。

2.1.5 算法复杂度

假设SCN模型中,输入层节点数为n,隐含层节点数为Lmax,输出层节点数为m,最大候选层节点数为Tmax,样本数量为N,那么SCN的复杂度是O(N×n×Lmax×Tmax+N×Lmax×m)=O(N×Lmax×Tmax)。对于CFSTOA算法,假设乌燕鸥的种群数量为K,最大迭代次数为zmax,种群中每个个体计算一次适应度函数f的复杂度为O(f),那么CFSTOA算法的复杂度为O(K×f×zmax),总复杂度为O(N×Lmax×Tmax×K×f×zmax)。

2.2 SCN参数的优化

如1.1关于SCN模型的问题陈述,由于r和λ对SCN的性能至关重要,下面给出利用CFSTOA算法来优化这2个参数的步骤。

1) 初始化CFSTOA和SCN。初始化种群数量K,比例因子ρ,最大迭代次数zmax,维数D,r和λ的上边界Ub、下边界Lb,隐含层的最大节点数Lmax,最大候选节点数Tmax,容忍误差ε。将r和λ按照算法1进行Tent映射,初始化Xi=(xi,r,xi,λ)(i=1, 2,…,K),xi,r和xi,λ分别代表r和λ。

2) 构建并训练SCN模型。将初始化的Xi根据文献[1]构建并训练SCN模型。

3) 更新参数。根据算法1更新r和λ。

4) 计算适应度值。将训练结果的均方根误差(root mean square error,RMSE)作为算法1中评估每个个体的适应度值,适应度值通过

(18)

计算。式中:ym表示样本m的实际值;fm表示样本m的输出值;M代表所有样本的总数。

5) 达到终止条件。当算法1达到终止条件或者SCN满足预设的容忍误差时,得到算法1的输出Xbest=(xbest,r,xbest,λ),否则重复步骤2)～5),直到满足终止条件。

6) 训练SCN。利用步骤5)中算法1输出的最优参数构建SCN,并通过训练得到最终结果。

3 实验评价

为了验证CFSTOA算法的有效性,以下通过求解函数全局最小值和优化SCN隐含层参数2个应用进行实验测试。实验在MATLAB R2018b环境下实现,所用计算机CPU为Intel(R) Core(TM) i5-9300H CPU@2.40 GHz,内存为8 GB,系统为WIN10 64位。

3.1 函数全局最小值求解

将2.1.2、2.1.3的共同改进的算法记为STOA1,2.1.1、2.1.3的共同改进的算法记为STOA2,2.1.1、2.1.2的共同改进的算法记为STOA3。本部分实验测试选取文献[21]实验中的部分基准测试函数,如表1所示。其中,f1(x)～f6(x)为单峰函数,f7(x)～f10(x)为多峰函数。将提出的CFSTOA算法与STOA、STOA1、STOA2、STOA3、灰狼优化(grey wolf optimization,GWO)算法、引力搜索算法(gravitational search algorithm,GSA)、粒子群优化(particle swarm optimization,PSO)算法、WOA、差分进化(differential evolution,DE)算法进行对比实验。算法的关键参数按照文献[22]设置(如表2所示)。为了保持实验的公平性,将CFSTOA算法的控制参数Cf也设置为2。将ρ设置为0.9可以保证在不干扰原本算法收敛性的情况下,使小部分种群可以通过反馈原则增加算法的局部搜索能力,如果ρ过大,可能会导致算法过早收敛,陷入局部最优。

表1 基准测试函数[21]Table 1 Benchmark functions[21]

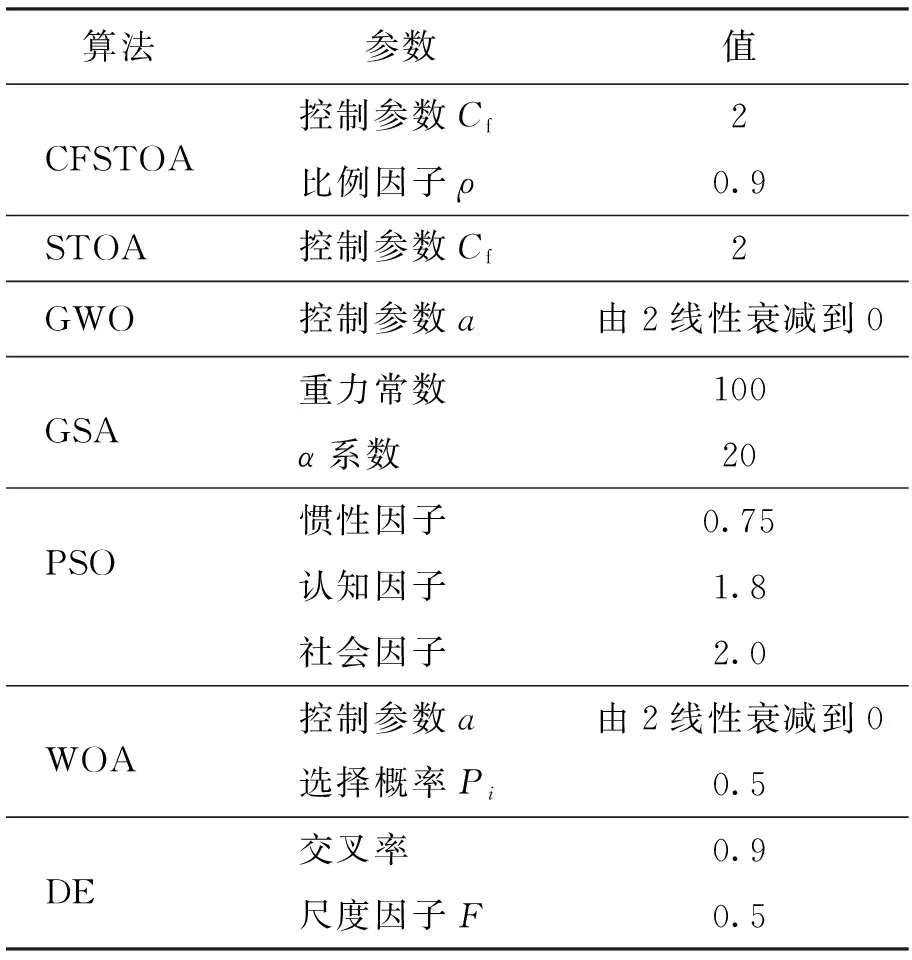
表2 各算法关键参数设置[22]Table 2 Key parameter setting for algorithms[22]

为保证实验结果的合理性,将每种算法的种群数量设置为30,最大迭代次数设置为500,每个算法独立运行50次。最后,统计每种算法所得结果的平均值和标准差,如表3所示。可以看出,在基准测试函数f1～f10中,CFSTOA算法的寻优精度和鲁棒性均优于其他对比算法。通过比较可以发现,STOA1和STOA2的收敛精度相仿,均优于STOA3算法,说明对乌燕鸥种群加入了劣势种群反馈原则后,增强了算法的局部搜索能力,提升了算法的寻优精度。在基准测试函数f5～f7中可以发现,STOA2算法收敛精度略低于STOA1,说明采用线性因子调节策略比混沌初始化策略对STOA

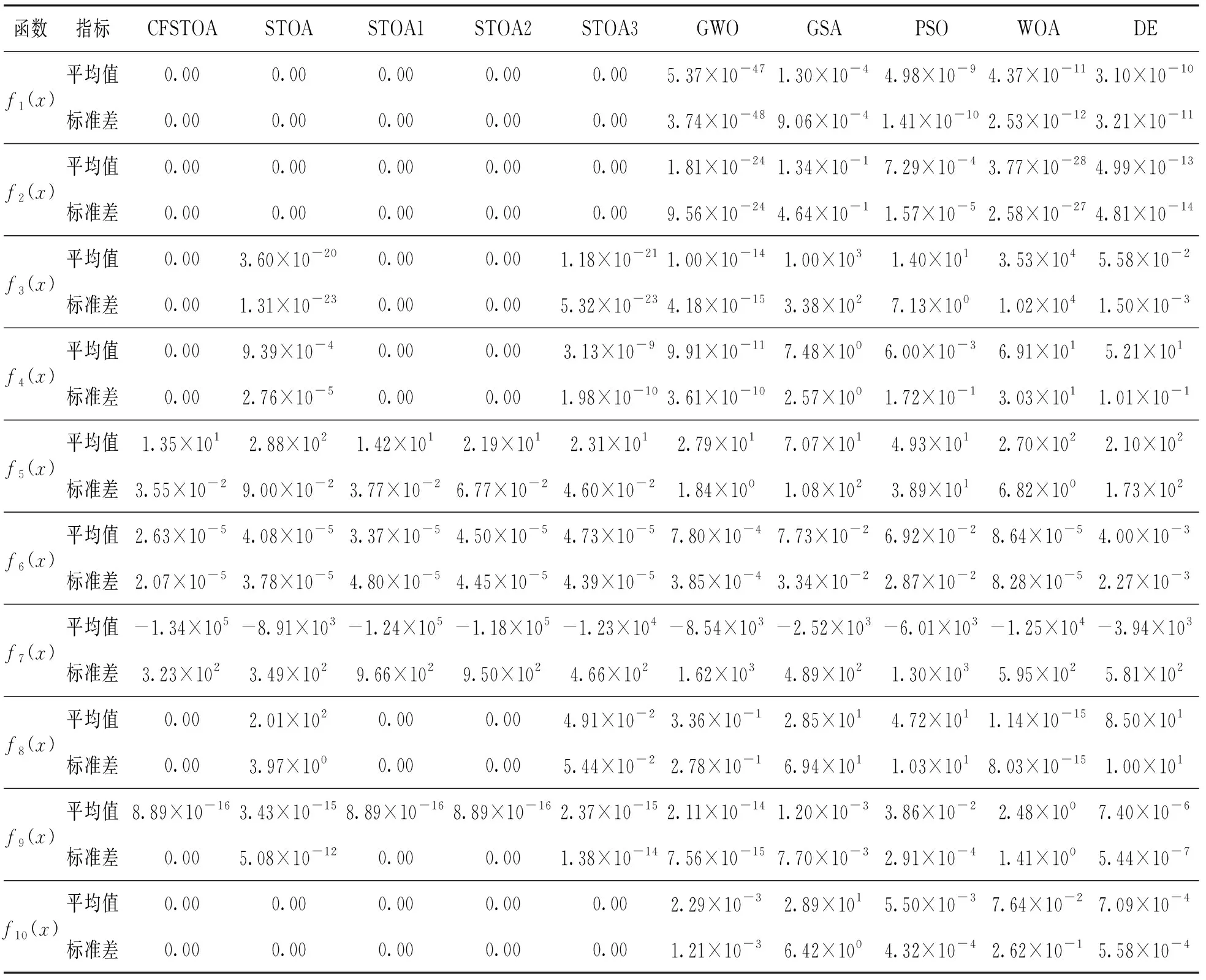
表3 不同算法的测试结果对比Table 3 Comparison of test results of different algorithms

的收敛精度提升更大,而CFSTOA算法的优化效果优于STOA1、STOA2算法,说明这2个策略相结合会使算法的寻优能力更好。

为了进一步分析上述10种算法的寻优能力,将每种算法在迭代过程中的收敛曲线进行了比较,如图2所示。可以看出,CFSTOA算法在迭代的前期可以快速收敛,说明改进后的随机变量CB由于在前期扩大了聚集距离,增强了算法全局搜索能力,使其在迭代前期收敛速度加快。另外,在迭代求解过程中,当STOA算法和其他算法过早收敛、陷入局部最优时,CFSTOA算法可以搜索到更好的全局最优解,这证明了CFSTOA算法的劣势种群反馈原则可以提高算法的寻优精度。

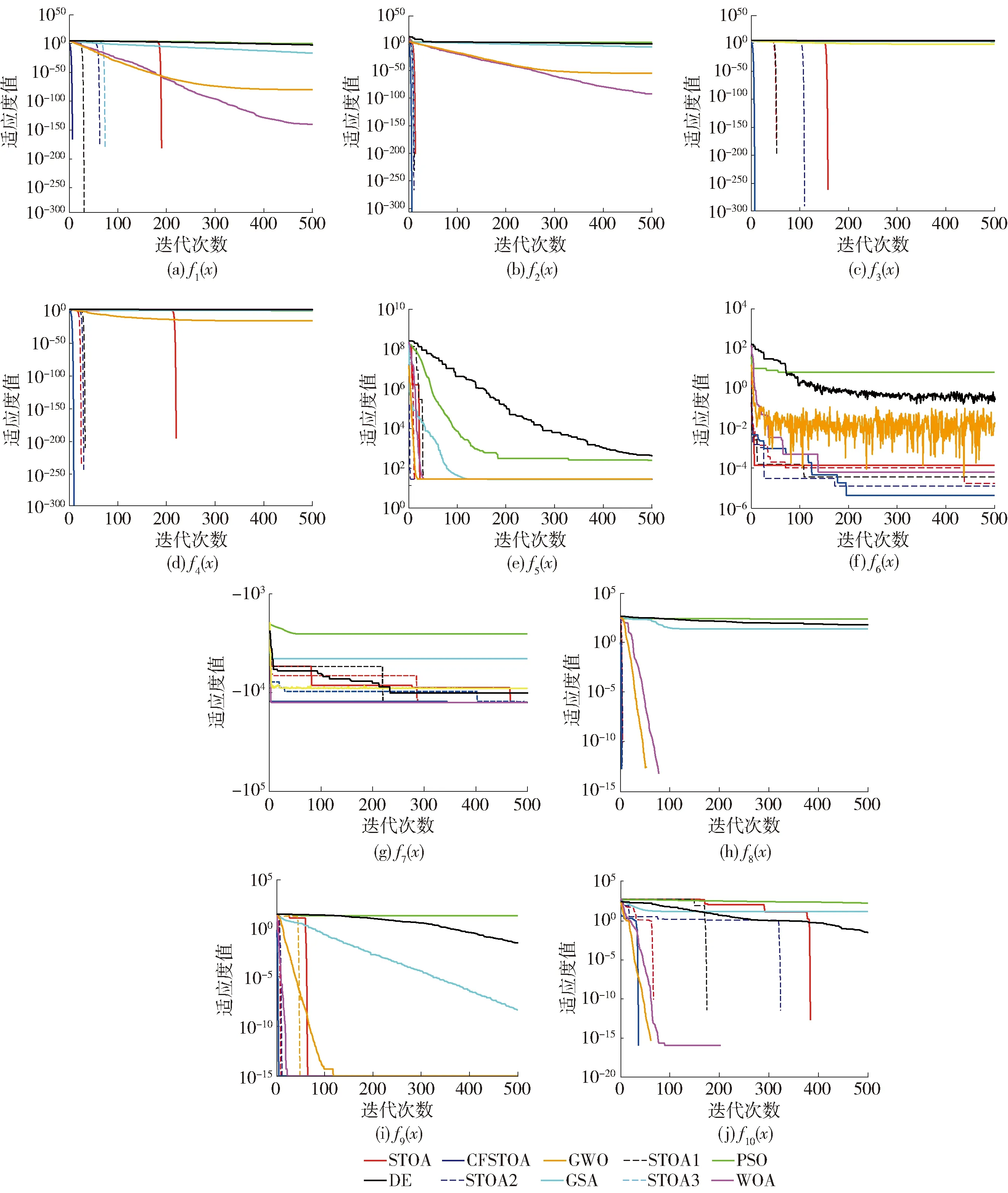
图2 不同算法的收敛曲线对比Fig.2 Comparison of convergence curves of different algorithms

3.2 CFSTOA的应用效果

为了验证提出的利用CFSTOA优化SCN隐含层参数的有效性,选取基于进化学习的知识提取(knowledge extraction based on evolutionary learning,KEEL)数据集提供的4个回归数据集(如表4所示)进行实验,并将CFSTOA算法优化后的SCN(记为CFSTOA-SCN)与随机向量功能链接(random vector functional link,RVFL)网络[26]、SCN进行对比,以此来考察CFSTOA-SCN的预测效率和预测精度。

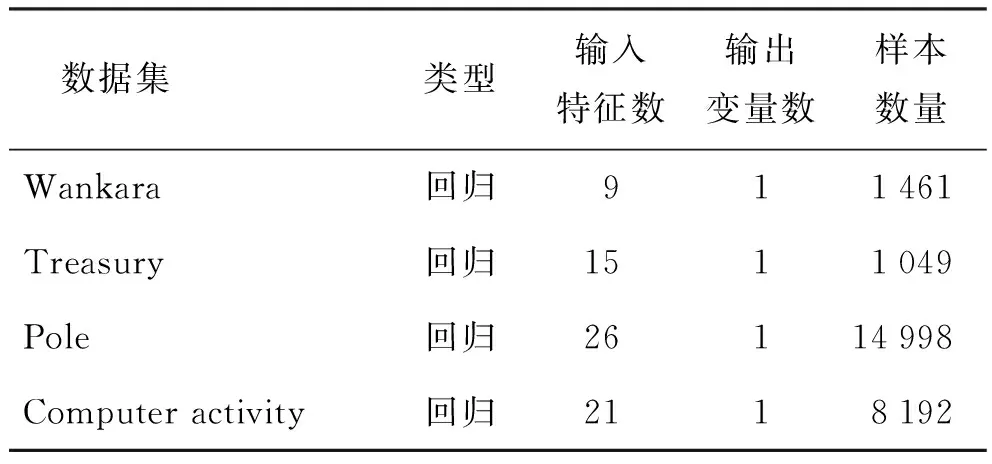
表4 回归数据集Table 4 Regression datasets

为了减少不同范围尺度特征的影响,采用归一化方法对输入输出向量进行预处理。通过

(19)

可以将原始数值映射到[0, 1]。式中:V为该属性的原始数值;V′为归一化的结果;Vmax和Vmin分别为a的最大值和最小值。

3.2.1 参数设置和评价指标

CFSTOA-SCN的参数设置如下:K设置为20,Cf设定为2,CB设定为[0,1],u和v设置为1,ρ设置为0.9,zmax设置为10,维度设置为2,Tmax设置为100,ε设置为1×10-3,r的上、下界分别设置为0.999 90、 0.900 00,λ的上、下界分别设置为250.0、0.5。RVFL网络的权重和偏差由[-1, 1]的均匀分布产生;SCN的r和λ分别由{0.900 00, 0.990 00, 0.999 00, 0.999 90, 0.999 99}和{0.5, 1.0,5.0, 10.0, 30.0, 50.0, 100.0, 150.0, 200.0, 250.0}自动确定。

随机选择每个数据集的50%作为训练数据,其余的样本数据作为测试数据。为了评价该模型的准确性,将RMSE作为评价指标。

3.2.2 结果与讨论

将RVFL、SCN和CFSTOA-SCN模型均独立运行100次,用RMSE的平均值和标准差以及训练时间来评价模型的性能。通过改变隐含层的Lmax得到RVFL、SCN、CFSTOA-SCN在4个数据集上的训练和测试结果(如表5所示)。可以看出,CFSTOA-SCN在Wankara和Treasury数据集上的训练和测试效果与SCN相当,优于RVFL网络。CFSTOA-SCN在Pole、Compactiv数据集上的训练和测试效果都优于其他方法,说明当数据集有较多样本量和特征数时,利用CFSTOA优化SCN隐含层参数可以有效提高SCN的回归精度。

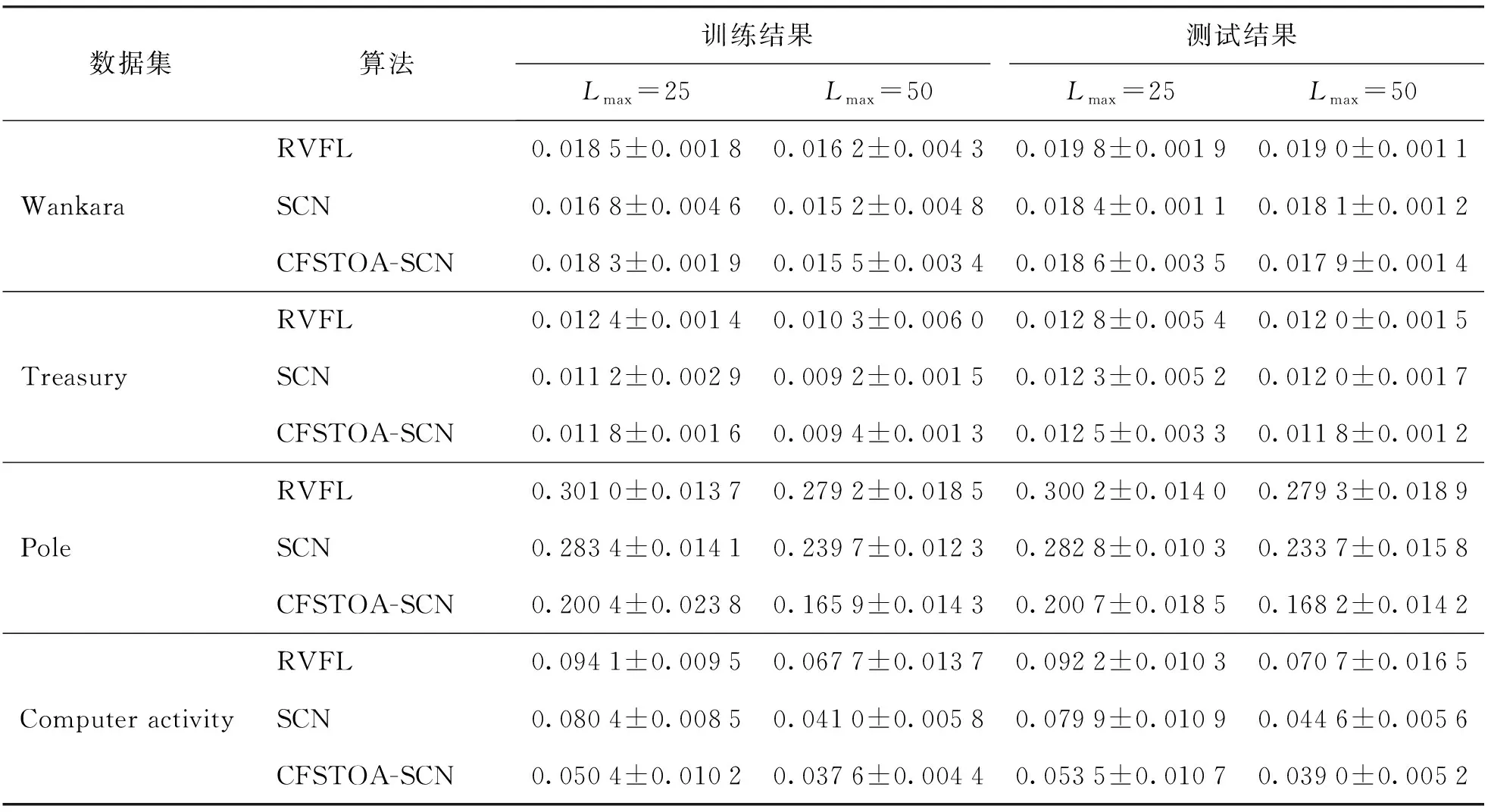
表5 不同算法在各数据集上的RMSE对比Table 5 Comparison of RMSE of different algorithms on each dataset

为了进一步验证CFSTOA-SCN的有效性,将CFSTOA-SCN和SCN在4个数据集上的训练时间(不包含CFSTOA算法的寻优时间)进行比较,结果见表6,以此观察参数优化前后SCN的训练速度。从表中可以看出,当Lmax为25、50时,CFSTOA-SCN在4个数据集的训练效率均优于SCN,说明确定最优的r和λ后,SCN的训练速度会明显加快。

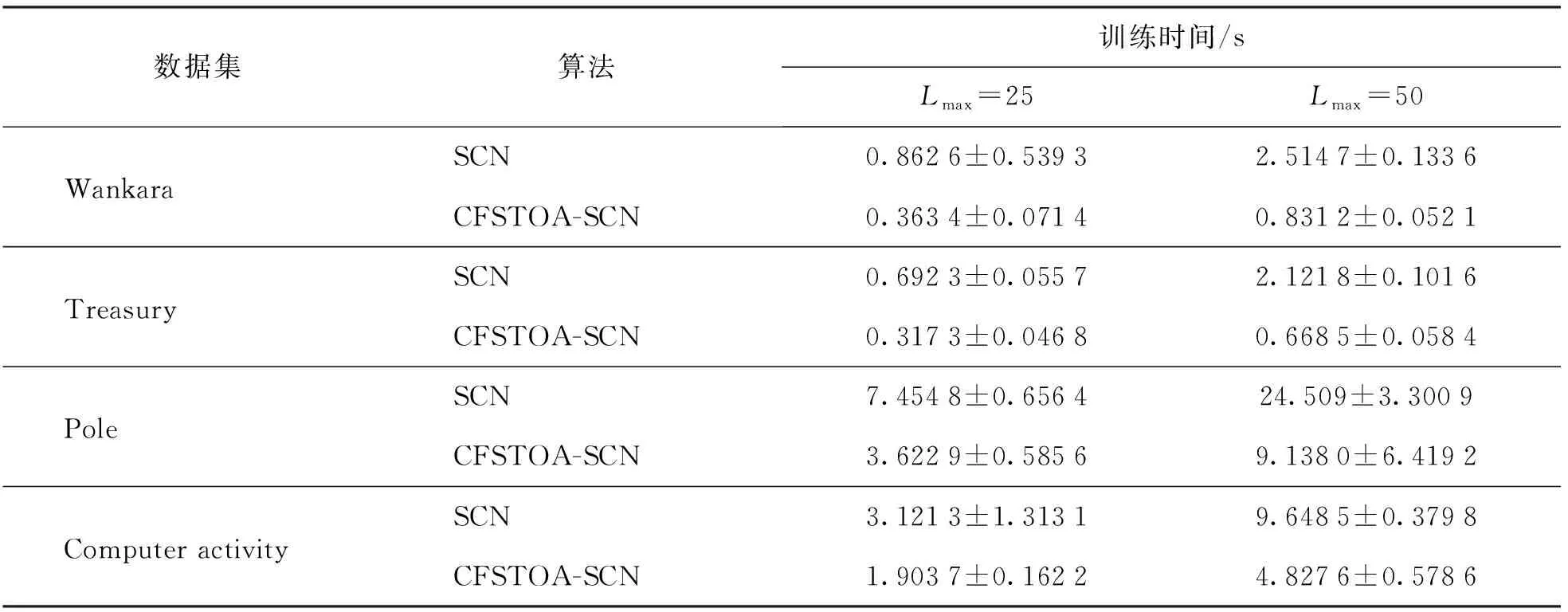
表6 CFSTOA-SCN与SCN的训练时间对比Table 6 Comparison of the training time of CFSTOA-SCN and SCN

图3～6显示了SCN和CFSTOA-SCN对4个数据集的拟合情况。从图3、4可看出,随着隐含层节点数的增加,CFSTOA-SCN的预测误差与SCN相当,而在图5、6中CFSTOA-SCN的预测误差要明显低于SCN,这进一步说明样本数量和特征数较多时,利用CFSTOA优化SCN隐含层参数可以有效提高SCN的回归精度。

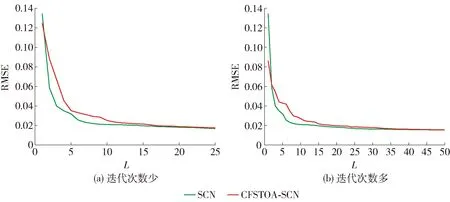
图3 CFSTOA-SCN和SCN在Wankara数据集上RMSE对比Fig.3 Comparison of RMSE of CFSTOA-SCN and SCN on Wankara dataset

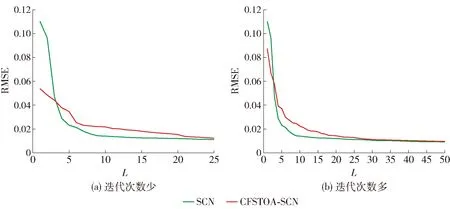
图4 CFSTOA-SCN和SCN在Treasury数据集上RMSE对比Fig.4 Comparison of RMSE of CFSTOA-SCN and SCN on Treasury dataset

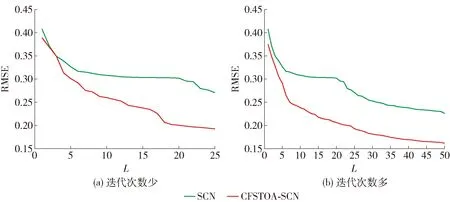
图5 CFSTOA-SCN和SCN在Pole数据集上RMSE对比Fig.5 Comparison of RMSE of CFSTOA-SCN and SCN on Pole dataset

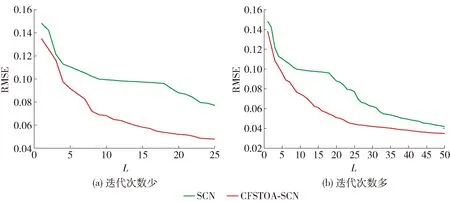
图6 CFSTOA-SCN和SCN在Computer activity数据集上RMSE对比Fig.6 Comparison of RMSE of CFSTOA-SCN and SCN on Computer activity dataset

求解函数全局最小值和优化SCN隐含层参数的实验结果表明,CFSTOA能有效处理函数极值求解问题,具有一定的普适性。另外,CFSTOA算法对SCN隐含层参数进行优化后,不仅有助于提高SCN的回归精度,而且可以加快训练速度。

4 结论

1) 混沌初始化策略的引入使得初始种群更具多样性,进而提升了算法的收敛性能。

2) 线性因子调节策略使算法在迭代前期扩大了聚集范围,增强了全局搜索能力,并在迭代后期缩小了聚集范围,增强了局部搜索能力,加快了算法的收敛速度。

3) 劣势种群反馈原则的引入,增强了算法在整个迭代过程中的局部搜索能力,提升了算法的收敛精度。

4) 对比实验表明,CFSTOA算法在收敛速度和收敛精度上均有显著提升,实现了全局搜索与局部搜索的动态平衡,不易陷入局部最优,在函数极值求解、参数优化领域具有一定的应用优势。

5) 文中的研究还存在一些局限性,这也可以作为以后的研究方向。首先,由于CFSTOA对SCN隐含层参数进行优化花费了大量的时间,可以通过简化CFSTOA来减少计算时间;其次,SCN已经扩展到了深度网络,如何对深度SCN进行参数优化可以作为下一步研究的重点。