基于Frenet-Serret框架的OFDR三维形状重构算法研究

辛玮　汪路军　刘煜　张学典　刘学静

关键词：三芯光纤；分布式形状传感；有限元；光频域反射仪；应变

中图分类号：O 439 文献标志码：A

引言

光纤形状传感是近年来一个新的研究方向，该技术在航天变形翼形状监测、手术导管跟踪、长距离电缆变形监测等场合都具有较高的应用价值[1-2]。光频域反射法（optical frequency domainreflectometry， OFDR）可以做到分布式测量，利用铺设在被测物体上的光纤，采用分布式测量光纤曲率的方法，通过一定的算法测量物体的形状和位置，具有较高的空间分辨率。由于多芯光纤适用于大曲率情况，具有芯间各项同性等优点，研究其重构算法具有很大意义。

Miller 等[3] 提出将光纤近似划分为圆弧，根据密切圆理论重构算法由分布式应变测量数据研究二维光纤形状传感。 Duncan 等[4] 结合OFDR技术，在一根1.1 m 的多芯光纤上蚀刻光纤布拉格光栅（fiber Bragg grating， FBG），实现了空间分辨率为1 cm 的二维和三维传感。Moore 等[5]采用基于空间微分几何的Frenet框架，将FBG传感器置于多芯光纤中测量应变值，用数值方法求解相应方程，从而重构了多芯光纤的形状。Khan 等[6] 分别在形状各异的模具中放入带有FBG 传感器的螺旋芯和直芯，发现螺旋芯更适合扭曲的测量应用。杨濠琨[7] 采用FBG曲面重构算法对机器人触手形状进行了重构。张新华[8]在基于正交曲率和Frenet 方程的三维重构算法之上设计了基于FBG的无人机翼和蒙皮形变检测系统。Khan 等[9] 利用Frenet框架，提出了一种基于四芯光纤的FBG 传感器测量数据，重建医疗导管中心曲线的技术。傅程[10] 利用Frenet框架对光纤二维形状进行了还原。国内外研究现状主要集中在FBG传感器与二维层面，FBG 传感器往往受限于环境变化的影响，而基于瑞利散射的OFDR 光纤传感技术能带来更高的空间分辨率，实现全分布式监测[11]。现有文献中尚未发现 OFDR 传感器结合Frenet 框架的三芯光纤三维重构的报道。

本文首先从理论上分析了光纤应变与光谱波长漂移量之间的物理关系，定义了三芯光纤表观曲率向量，推出曲率和挠率的计算公式，引入Frenet-Serret 公式和插值拟合处理方法计算得出三维形状还原曲线的积分方程； 接着利用ANSYS 有限元仿真软件对S 形应变数据进行建模并提取，代入算法并重建S 形光纤；最后对重构误差进行分析并提出改进措施。

1 形状重构算法设计

1.1 理论基础

光频域反射技术通过测量传感量产生的相位改变，采用相位补偿思想，在解调后得到的光谱变化能反映应变、温度等传感量的变化程度[12]。瑞利背向散射光谱的变化受应变与温度的影响可表示为

要实现三维空间形状的测量，需要选取均匀分布的至少3根单模光纤或者三芯光纤对物体形状改变的应变进行测量[13]。三芯光纤在弯曲时不容易受到损坏，具有较高的可靠性和可操作性，相比四芯或七芯光纤，三芯光纤更容易控制和操作，使得OFDR 测量更加精准、高效。此外，三芯光纤的体积小、成本低，可以更轻松地安装在测量物体上，更好地满足大规模的测量需求。因此，本文选择三芯光纤作为研究对象。

在应变测量时，同一环境下温度基本保持不变，因此温度的变化往往可忽略。对K_ε进行标定之后，得到各个芯的频谱漂移量和应变的对应关系。随后采用合适的还原算法，对三维空间的光纤进行原始形态的还原。

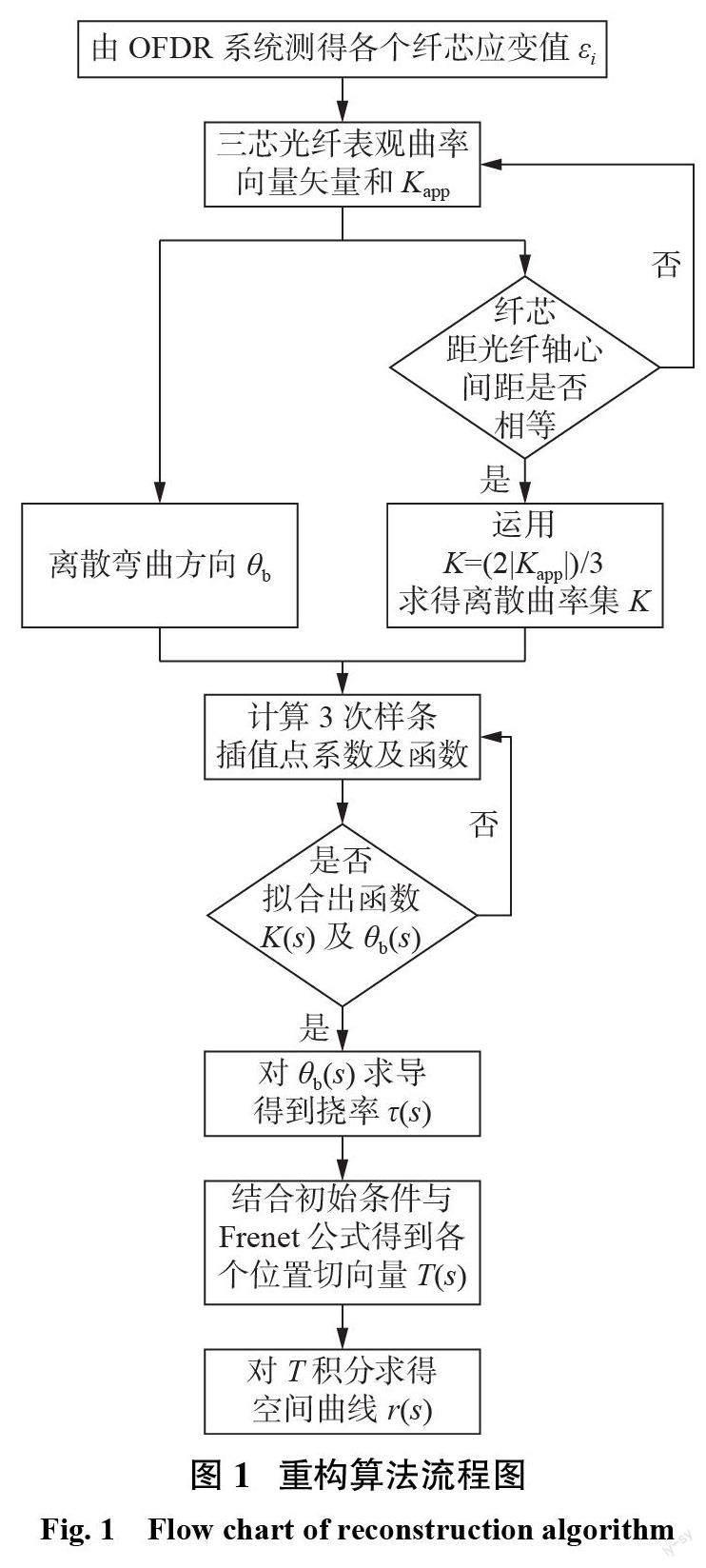
郭雅美[14] 提出了基于OFDR形状传感重构算法，本文在此基础上，加入样条插值拟合，具体流程如图1 所示。

一般运用于形状传感的三芯光纤的截面图如图2所示。这里省略了涂覆层，光纤由纤芯、包层组成，纤芯之间以周向120°排布。θ_i是局部坐标系的y 轴正方向与第 个纤芯位置之间的角度，θ_b是局部坐标系中y 轴与光纤弯曲方向之间的角度，r 是纤芯与光纤几何中心之间的距离。

2 分析与讨论

2.1 模型建立

本文利用Ansys workbench 建立了三芯光纤有限元模型来验证算法的正确性，选取有利于提高计算精度的solid186 单元，建立了如图3 所示的简化几何模型，光纤总长为50 mm。三芯光纤材料的具体参数如表1 所示。

2.2 重构分析

为了更好地展现出光纤的三维形变，本文设定的光纤变形情况为S 形弯曲，从平面S 形弯曲的基础上拓展到空间S 形弯曲，分别测量出弯曲时的位移云图与轴向应变分布图，与应变分布的实际情况进行比较分析。最后将初始边界条件和纤芯弯曲数据代入相关公式，运用本文算法重构出三芯光纤的曲线方程。

首先在15 mm 和35 mm 处分别施加两个方向相反的1 mm 位移载荷，使三芯光纤产生二维面上的S 形弯曲，求解后得到的位移云图如图4 所示。

结合光纤长度分别提取3 个纤芯的轴向应变值，绘制了平面S 弯曲时3 个纤芯的轴向应变分布曲线图，如图5 所示。

拓展到三维空间，将原35 mm 处所施加径向1 mm 位移载荷转换到正交方向，其余条件不变，使三芯光纤产生空间S 形弯曲，提取3 个纤芯应变数据，通过本文算法重构光纤的形状。求解后得到的位移云图如图6 所示。

结合光纤长度分别提取3 个纤芯的轴向应变值，绘制了空间S 弯曲时3 个纤芯的轴向应变分布曲线图，如图7 所示。

由图4、5 可知，平面S 弯曲时两端位移较小，弯曲部位位移最大，最大值为0.001 m 左右，光纤上的位移分布与弯曲情况相符；纤芯2 和纤芯3 应变分布曲线几乎重叠，变化走势趋于一致，和纤芯1 的变化趋势相反，在光纤的末端应变值趋于0。应变分布符合平面上S 弯曲时纤芯的实际情况。

由图6、7 可知，空间S 弯曲时两端位移较小，弯曲部位位移最大，最大值为0.001 m 左右，光纤上的位移分布与弯曲情况相符。纤芯1 和纤芯2 的轴向应变值趋势一致，和纤芯3 相反，在光纤的末端应变值趋于0。应变分布符合空间S 弯曲时纤芯的实际情况。

将初始边界条件和纤芯弯曲数据代入式（10）和式（14），即可重构出三芯光纤的曲线方程。三芯光纤的重构曲线方程可由初始边界条件和纤芯应变数据得到，对于光纤实际曲线，在ANSYS 仿真软件的模型中间建立path，分别提取每个位置在x， y 方向的变形得到。图8 所示为光纤实际曲线对比重构曲线图，由图可知，该算法还原光纤三维形状的效果非常好。

由图可见，位置误差随着光纤长度的增加逐渐增加，最大位置误差在末端。误差来源主要是对弯曲曲率和弯曲方向的样条插值误差以及Frenet 框架还原会出现奇异点等问题。均方根误差计算结果为0.996 mm，计算得到单位长度误差最大值为0.082 4%。

3 结论

本文设计了基于Frenet-Serret 框架的OFDR三维形状重构算法，并利用有限元仿真软件Ansys workbench 建模S 形弯曲时的三芯光纤，提取应变进行了算法验证。通过OFDR 瑞利散射光谱波长漂移可以得到纤芯的应变分布数据，再结合本文的重构算法可以重构三芯光纤的形状。因为运用OFDR 设备进行实验获取应变数据比较繁琐，本文直接利用有限元软件仿真三芯光纤三维形状的S 形变化，并且得到每个纤芯的离散应变数据以及空间坐标系下的坐标数据。本文还原算法存在累积误差，即位置误差随着光纤长度的增加逐渐增加，误差来源主要是3 次样条插值时产生的误差以及Frenet 框架还原会出现奇异點等问题。均方根误差计算结果为0.996 mm，单位长度误差最大值为0.0824%。未来将采用更高阶的样条插值方法，减小3 次样条插值处理时带来的误差；在还原过程中将曲率限制在一个合理的范围内，从而有效避免还原时奇异点问题。本研究为更深入地研究OFDR 形状检测提供了重要的理论基础，研究结果具有一定的工程应用价值。未来将以本研究为基础，进一步探讨减小算法累积误差的方法，探究长尺寸、大形变的光纤重建。