构建利用数学辅助工具的问题解决模型

王治才

摘 要：小学生抽象思维能力薄弱，在解题过程中常常面临着诸多困境.鉴于此，可充分借助线段图这一辅助工具，将抽象问题具体化、直观化，帮助学生读懂题意，明确其中蕴含的数量关系，厘清解题思路等.本论文就以此作为研究的新视角，结合线段图在小学数学解题中的具体应用进行了详细的探究，最终提出了在日常教学中小学生运用线段图的重要价值.

关键词：核心素养；小学数学；线段图；解题教学；应用价值

在小学数学课堂教学中，问题解决是最为重要的组成部分.学生在解决问题的过程中，不仅对所学的知识进行了巩固、内化，也逐渐形成了系统化的知识体系，为新知识的学习提供了深厚的“土壤”；同时，解决问题的过程，也是数学思维活动的过程，更是知识迁移和应用的过程，是培养学生数学思维、知识应用能力的重要途径.但是在具体的教学中，问题解决题目形式多种多样、涉及面非常广泛，对小学生的理解能力提出了更高的要求.在部分的数学题目中，条件常常是隐藏在题目中，学生必须要经过分析，才能获得明确的解题思路.鉴于小学生思维能力薄弱的现状，唯有充分借助线段图这一辅助性的解题工具，将抽象的文字直观化，帮助学生顺利找到隐藏的条件，才能逐渐形成明确的解题思路.

1 基于线段图理解题目含义

理解题目是解题的基础和关键，学生只有读懂题目意思，弄清楚题目要求，才能借助数量关系分析，形成正确的解题思路.但就目前而言，许多小学数学应用题的文字语言描述比较抽象，学生往往读完一遍，都不知道题目的真正含义，甚至还会出现误解的现象.面对这一现状，在引导小学生进行解题时，就可充分发挥线段图这一辅助工具的作用，将题目的意思形象地表达出来.

例1 周末，妈妈去超市买了一袋水果，其中有20个梨，香蕉的数量是梨的2倍，猕猴桃的个数则比梨多3倍.问：妈妈买的水果中，有多少根香蕉？多少个猕猴桃？猕猴桃比梨多多少个？

解析：学生在阅读这一题目的时候，受到自身思维发展水平的制约，常常出现一定的错误：部分学生只要一看到“谁比谁多”，潛意识中就会想到加法运算；一看到“谁比谁少”，潜意识中就会选择减法进行运算，但是这种解题思维却是错误的.而在题目中给出了“猕猴桃的个数则比梨多3倍”，学生在读题的时候，常常将其理解为猕猴桃是梨的3倍.面对这一现状，在引导学生理解题意的时候，就可指导学生一边读题，一边绘制线段图（如下图1所示），将题目的意思正确地表达出来，使得学生结合线段图清晰地认识到“多3倍的含义”.

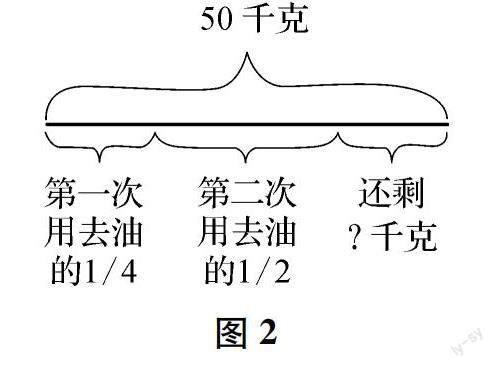
例2 （1） 有一桶油，其重量为50kg，第一次将桶中的油倒出了四分之一，第二次又倒出油的二分之一，这一桶油还剩下多少千克？

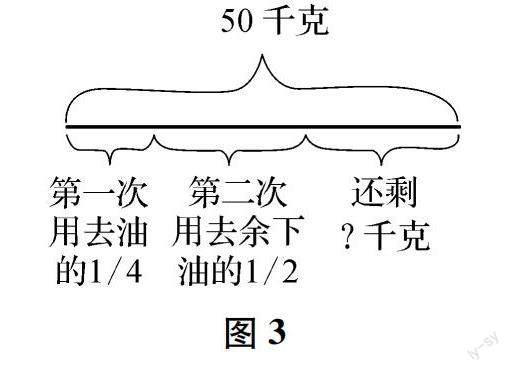
（2） 有一桶油，其重量为50kg，第一次将桶中的油倒出了四分之一，第二次又倒出余下油的二分之一，这一桶油还剩下多少千克？

解析：在对这两道题目进行解答的时候，学生常常会出现错误，其主要原因就是在对题意进行判断的时候出现了误差.学生在解题的时候，常常忽视题目（2）中“余下”的二分之一，而是按照题目（1）的解题思路进行解答.鉴于此，在带领学生分析题目意思的时候，就可充分借助线段图这一工具，将文字转化成为直观、形象的线段图（如图2、3）.

如此，在线段图的直观表示下，学生就可迅速理解题目含义.在针对（1）分析中，将一桶油一分为四，第一次用去了四分之一，即：50×1/4；第二次用去油的二分之一，即：50×2/4；在（2）题目中，第一次用去了四分之一，即：50×1/4；第二次用去的量转变为剩余的二分之一，即：50×（1-1/4）×1/2.如此一来，在线段图的辅助下，学生就可精准判断题目的含义，有效规避了解题中的错误现象^［1］.

2 基于线段图明确数量关系

在小学数学解题中，精准找出题目中的数量关系，是打开解题思路的“钥匙”.但是在具体的解题中，部分数学题目中的数量关系不甚明确，学生往往读了两三遍都毫无头绪，致使其难以找到具体的解题思路.鉴于此，在开展解题教学时，就可充分发挥线段图的辅助价值，将题目中隐含的数量关系直观地展示出来，帮助学生将数学关系模型构建出来.

例3 王大妈家中养90只鸡，鸭比鸡的数量多1/3，养的鹅则比鸭少1/3.那么，王大妈家中养的鸡和鹅的数量一样多吗？如果不一样多，是鸡多还是鹅多，多多少？

解析：在对这一题目进行解答的过程中，由于小学生刚刚接触分数的相关问题，在理顺这一题目关系时，关键点在于对“多1/3、少1/3”的理解，而学生常常将其误认为一致，导致学生解题出现错误.面对这一现状，在引导学生明确数量关系时，就可借助线段图这一辅助工具，将其直观地表示出来（如图4所示）.

从这一线段图中，学生就会清晰地认识到“多1/3、少1/3”所代表的含义有所不同，鸭比鸡多1/3，多的是鸡的1/3；鹅比鸭少1/3，少的是鸭的1/3.在理顺题目中的数量关系之后，就可计算出：鸭的数量=90×（1+1/3）=120；鹅的数量=120×（1-1/3）=80，最终顺利解答这一问题.

例4 甲、乙两辆车分别从A、B两地同时出发，两车相向而行.已知A、B两地之间的距离为180km，甲车的速度为60km/h，乙车的速度为40km/h，甲、乙两辆车经过几个小时之后，两者之间相距30km？

解析：这一题目相对比较难，主要是因为甲乙两辆车处于不断的运动之中，而在运动的过程中，符合题意的现象包括两种，即：两车相遇之前距离30m、两车相遇之后再次相距30m.在针对这一题目解答时，如果不借助线段图，小学生几乎无法找到其中蕴含的数量关系.鉴于此，就可指导学生运用线段图将这两种现象表示出来（如下图5所示）^［2］.

通过这一线段图，就将题目中复杂的数量关系直观、形象地展示出来，学生则可结合分析，将题目中的数量关系明确出来：相遇前：（180-30）÷（60+40），相遇后：（180+30）÷（60+40），最终完成这一题目的顺利解答.

3 基于线段图形成解题思路

小学数学解题的过程，也是培养和发展学生数学思维能力的过程.同时，学生在审题、分析问题、理顺数量关系时，唯有具备极强的思维能力，才能顺利解决相关问题.但是在具体的解题教学中，由于小学生当前思维特点以具体形象思维为主，教师应充分发挥线段图的价值.

例5 今年，父亲的年龄是儿子年龄的4倍，20年后父亲的年龄为儿子年龄的2倍.问：父亲和儿子今年的年龄是多少？

解析：这一道数学题目在小学阶段尤为常见.在具体解题的时候，如果不借助线段图，学生在阅读题目时就会产生各种疑惑的现象.鉴于此，就可指导学生一边阅读题目，一边结合题目的含义画线段图（如图6所示）.根据题目意思得知：今年父亲的年龄是儿子的4倍，可将儿子的年龄用一份线段图表示出来；父亲是儿子年龄的4倍，则为4个线段图.再过20年之后，就是在儿子和父亲年龄的线段图之后各增加20.之后，再结合“20年后父亲的年龄为儿子年龄的2倍”这一含义，得出数量关系：（1份年龄+20岁）×2=（4份年龄+20岁），最终顺利解决这一问题^［3］.

例6 小丽从家去学校，走到全程5/6处是光明超市.小丽放学回家的时候，走到全程1/3处是儿童医院.已知儿童医院和光明超市之间的距离为120m.问：从小丽家到学校一共有多少米？

解析：在对这一道常见题目进行解答的时候，学生常常一筹莫展，不知道如何解答.面对这一现状，就可充分发挥线段图的辅助价值，引导学生在阅读题目的时候，利用线段图将小丽家、光明超市、儿童医院、学校的位置标示出来，形成形象的感知（如图7所示）.如此，借助线段图的辅助，结合题目中给出的已知条件，引导学生思考只要确定了“儿童医院和光明超市之间的距离”占据全部距离的几分之一即可.如此，在线段图的辅助下，学生就很快找到了解题的“突破口”，计算出儿童医院和光明超市之间的距离占据全部距离的：1/3-（1-5/6）=1/6，最终计算出全部距离.

4 基于线段图培养学生规避解题错误

在小学数学解题教学中，还应在日常教学中，培养学生逐渐养成良好的解题习惯.针对小学生来说，受到思维特点的制约，小学生在解题时常常遇到固定的字眼，就会不假思索运用定势思维进行解题.这是一种非常危险的信号，若不及时进行纠正，就会对学生日后的数学解题产生很大的影响.鉴于此，小学数学教师在日常解题训练中，就应立足于线段图的价值，培养学生的画图意识和习惯.

例7 姐姐有10支铅笔，弟弟有4支铅笔.姐姐给了弟弟几支铅笔之后，两个人的铅笔数量一样多？

解析：这是一道小学二年级的数学题目，二年级的小学生在解题的时候，极容易受到固定思维的影响，一看到题目中的固定字眼，首先就会想到运用减法进行计算.如果教师按照学生的错误思路进行追问，学生才会意识到自己已经算错了.面对这一现状，教师在引导学生开展错题分析的时候，就可充分发挥线段图的价值，带领学生结合题目进行画图（如下图8所示）.

通过这一线段图，小学生就会恍然大悟，原来要想两人一样多，就是要把多出部分的一半分给弟弟即可.如此，不仅帮助小学生顺利解决这一问题，也促使其在学习的过程中，逐渐形成了强烈的画图意识和习惯，为日后的学习奠定了坚实的基础.

例8 妈妈和小红两个人的年龄之和是44岁，妈妈比小红年龄的4倍小1岁.问：小红和妈妈的年龄各为多少岁？

解析：这是一道三年级的数学题目，小学生在解答这一问题的时候，依然会受到固定思维的影响，看到“4倍小1岁”，就理所当然地选择了减1的方式.为了规避学生在解题中出现常见错误，在日常教学中，就可引导学生绘制线段图（如下图9所示）.

经过线段图分析，学生可发现原来的固定思维中存在的错误，发现妈妈年龄+1之后恰恰是小红年龄的4倍.以此作为突破口，将小红的年龄看做是1份，妈妈的年龄+1看做是4份；之后，根据两人年龄之和为44岁，得出44+1恰恰是5份年龄之和，最终计算出两人的年龄.由此可见，在小学数学解题中，通过线段图的应用，不仅规避了常见的错误现象，也有助于学生在解题时逐渐形成一定的画图意识，形成良好的做题习惯等，最终为其更好地开展数学学习奠定坚实的基础^［4］.

5 解题教学中应用线段图的反思

结合上述例题分析得知，小学线段图在解题教学中发挥了十分重要的价值：一方面，契合了小学生的认知发展特点.针对小学生来说，由于其认知思维发展水平比较低，在日常解题中常常面临着无法正确理解题目、找不出数量关系、找不到解题突破口等困境，导致其在解题的时候处处碰壁.长此以往下去，就会严重影响小学生的学习自信心.而通过线段图的应用，借助形象、直观的感知，有效解决了小学生在解题时面临的诸多困境，使其在快速解题的过程中获得了良好的情感体验，有助于帮助学生树立学习自信心；另一方面，有助于提升学生的问题解决能力，促进学生思维的发展.在小学数学教学中，应用题目是教学的重难点，通常具备一定的难度，+学生不仅要具备系统化的知识体系，还应具备一定的知识迁移

和应用能力.鉴于此，通过线段图的应用，帮助学生顺利读懂题意，并从不同的角度展开分析，在正确思路的引导下，找到问题解决的突破口.经过一段时间训练之后，小学生的知识迁移、问题解决、思维能力等都会随之提升.

鉴于此，小学数学教师在日后的数学教学中，应有意识、有计划地培养学生的画线段图习惯，使得学生在训练中逐渐掌握这一解题方式.尤其是在初期的时候，小学生常常面临着无从下手的问题，教师应借助示范和耐心指导，引导学生在阅读题目中结合关键词理清条件关系或者数量关系，并结合题目中给出的数值绘出相一致的线段图^［5］.

6 结束语

综上所述，鉴于数学学科的特点，数学学科承担着培养学生问题解决能力、数学思维的重任，旨在激活小学生的思维，促进其从低阶发展到高阶思维中，并在学习的过程中逐渐形成运用所学知识解决实际问题的能力.鉴于此，在开展问题解决教学时，必须要立足于小学生的年龄特点、思维发展水平等，融入线段图这一辅助工具，帮助小学生顺利克服解题中面临的种种困难，最终达到顺利解决问题的目的.

参考文献：

［1］ 宋书璐.图示法在小学数学“数与代数”教学中的运用研究［D］.云南师范大学，2021.

［2］ 吴红梅.利用线段图巧解应用题——线段图在小学数学应用题教学中的应用策略探究［J］.考试周刊，2021（10）：81-82.

［3］ 韩淑霞.线段图：让数学解题从模糊走向明晰［J］.数学教学通讯，2020（22）：87-88.

［4］ 王雯.线段图在小学数学应用题解题中的作用［J］.新课程教学（电子版），2019（15）：90.

［5］ 阿旺热旦.线段图在小学数学应用题教学中的应用策略［J］.新课程（上），2017（8）：104.

［6］ 張琳.小学数学应用题教学线段图的应用分析［J］.课程教育研究，2017（2）：140-141.