新建普通住宅房价指数面板数据模型构建及应用

何赛琦，金升平，陈家清

（武汉理工大学 理学院，武汉 430070）

0 引言

中央经济工作会议上多次强调“房住不炒”，要全面落实因城施策，促进房地产业的良性循环和平稳健康发展。准确的房屋价格指数是评估房地产市场平稳健康的重要依据，因此科学且方便地编制房屋价格指数具有重要的理论和现实意义。由于国家已严格控制或禁止高档住宅的建设规模，同时取消了使用经济适用房的价格数据来编制房价指数，因此针对我国新建普通住宅的价格指数编制问题进行研究具有重要的意义。然而，住宅存在异质性，没有两套住宅是完全同质的，指数编制的同质要求与住宅异质的矛盾造成房价指数编制理论面临巨大困难。国外学者提出了特征价格模型和重复交易模型，国内学者近年来结合我国的房地产实际，也取得了房价指数编制方法的系列研究成果。但是，仍然存在一些理论和实践上的问题，需要通过不断地研究和改进，以得到科学准确的房价指数编制模型与方法，更为准确地度量我国普通商品房的价格变化情况，为政府制定合理的房地产政策提供更科学的依据。

1 方法介绍

1.1 特征价格法

特征价格法将房价与房产的结构特征、邻里特征和环境特征联系起来，建立房价与各种特征之间的回归模型，并利用该模型预测房价水平。

特征价格法可以调整房产样本的异质性，在理论上具有一定优势。但在实际应用中，特征价格法需要收集大量特征变量的数据，而且不同城市或同一城市的不同发展阶段，房屋的特征变量可能有较大变化，有些特征变量难以量化。在具体应用时，若某些特征变量缺失或特征函数的形式设置不当，所编制的房价指数反映出来的房价变动情况会与真实房地产市场存在偏差。因此，采用特征价格法编制我国新建普通住宅房价指数不具备普适性。

1.2 重复交易法

重复交易法试图通过发生过两次或两次以上交易的样本数据来消除房屋样本的异质性，从而回避特征价格法选择特征变量的难题[1]。

在实践中，由于重复交易的样本数量较少，因此重复交易法存在样本的代表性较差问题[2]。而且我国新建普通住宅的交易只有一次交易记录，这些问题使得重复交易法难以直接应用于我国新建普通住宅的房价指数编制。为克服以上问题，有学者提出类重复交易规则，利用平均的思想将同一楼盘不同时期销售的房产转化成具有同质性的产品的“重复交易”，并将重复交易法应用于我国新房市场，对我国房价指数编制模型的完善具有重要意义。但是，以中间楼层的单价作为配对后房产的均价可能存在平均过度的问题。还有学者提出拟（伪）重复交易模型[3]，将且只将同一匹配空间内相邻时间上的两个样本看作一个匹配对。闵继勇（2018）[4]基于同一小区内不同时期交易的房产来构造有序交易对提出类重复交易法，但当匹配房产分布差别较大时可能会导致误差过大。先倚懿和金升平（2016）[5]通过对新建普通住宅现有的交易数据及其结构特征进行研究，采用插值法产生虚拟重复交易数据，该方法能有效扩充样本数据，但是模拟数据与真实数据间的偏差可能导致计算的房价指数准确性不足。

1.3 样本匹配法

McMillen（2012）[6]基于特征价格法，将重复交易法置于匹配的框架下进行研究，并利用倾向值进行匹配，提出了房价指数编制的匹配模型。然而，基于倾向值的匹配模型要求较大的样本规模，在某些狭窄的共同支持域设定下，一些干预组房产可能找不到匹配的控制组房产或者一些控制组房产可能并不被使用，这会导致房价指数信息损失，存在与特征价格法类似的问题。金升平等（2017,2019）[7,8]、董艳玲等（2020）[9]基于上下楼集合生成匹配对来构建匹配模型。

为分析方便起见，本文给出“上下楼集合”的概念[8]。图1 是一栋楼房的一个单元结构，每层有两套商品房，其总楼层或总高度为6，A1—A6为一个上下楼集合，其与B1—B6分别为不同的上下楼集合。

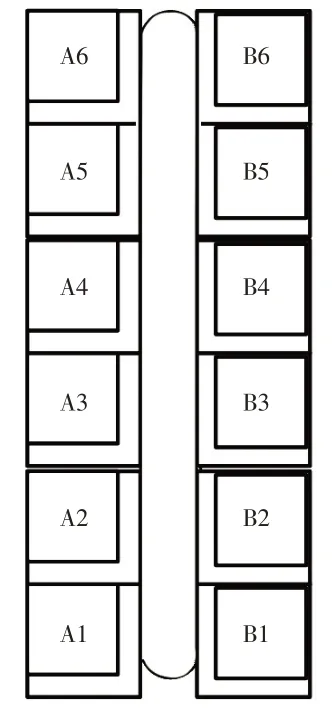
图1 上下楼集合

引入上下楼集合概念可以更好地处理我国城市居民对住宅朝向十分敏感的问题。本文将属于同一上下楼集合的房产按一定的顺序组成匹配对[7—9]，建立了房价指数的匹配模型，最终归纳出一个普通的线性回归模型：

基于OLS得到参数的估计公式：

如果同一上下楼集合中收集了3 层商品房的样本数据fli1、fli2、fli3，则在这3 个样本中模型（1）有3 种方法选择 匹 配 对：(fli1，fli2) 和(fli2，fli3) 、(fli1，fli2) 和(fli1，fli3) 、(fli1，fli3)和(fli2，fli3)。虽然从模型（1）和实际背景来看，3种选择方法都可以，但从参数估计的角度来看，计算的结果不一样。

假设式（1）为以一定方式选择匹配对对应的回归方程，则以另外方式选择匹配对对应的回归方程为：

如果仍假定Pε是独立同分布的，那么利用OLS 计算的式（2）来估计式（3）中的参数β，结果为[(PX)T(PX)]-1(PX)TPy=(XTPTPX)-1XTPTPy。由于PTP=I不成立，因此回归方程（1）与回归方程（3）估计的参数不再相等。

以上论证说明，基于匹配模型，当属于同一个上下楼集合的样本组成匹配对的方式不同时，用OLS所估计出的房价指数是不同的。房价指数的所有重复交易模型中都存在类似的问题[3]。

2 模型设计

2.1 房价指数的纵向非平衡面板模型

我国新建普通住宅同一上下楼集合中的房产面积、朝向和房间结构都基本相同，具有较高的同质性。房产价格不同主要是所在楼层不同或者销售时间不同造成的，因此，在建立房价指数编制模型时可将同一上下楼集合中的所有交易房产当作一个整体来研究。由于并不是所有上下楼集合中的房产在每个月均会产生交易，故用来编制房价指数的房产交易数据在时间上是非平衡的。而且在某个上下楼集合中，某个月份可能有两套及以上的房产被销售，这时被观测的样本在时间上是重复的。综上，将上下楼集合作为整体来研究的房产交易数据集构成纵向非平衡面板数据集。

为了统一处理不同高度的楼栋，使用房产的标准高度来反映房产的楼层特征。对于不同的楼栋类型，房价随高度变化的趋势也不相同，故在模型中加入楼栋类型与房屋标准高度的交互项。表1为变量说明。

表1 变量说明

建立新建普通住宅房价指数的纵向非平衡面板数据模型：

其中，βti，j表示时间ti，j的固定效应，也是房价指数的对数，记β0为基期房价指数的对数，取β0=0；α1和α2分别为标准高度和标准高度平方的固定效应；γ1和γ2分别为楼栋类型与标准高度和标准高度平方的交互效应；μi表示第i个上下楼集合的效应；vi，j表示剩余的随机扰动项，vi，j～N(0，σv2)；N表示上下楼集合的总数；ni表示第i个上下楼集合中交易的房产总个数，ni≥2。

当μi都是确定性参数时，称式（4）为纵向非平衡面板固定效应模型；当μi都是随机变量时，称式（4）为纵向非平衡面板随机效应模型。

纵向非平衡面板模型（4）的数据要求i=1，…，N，ni＞1，意味着每个上下楼集合至少有两套商品房销售。

文献[7]设定价格指数为较一般的半线性模型：

若令f(Li，Oi)=μi，则μi是第i个上下楼集合对应的固定效应。所以模型（5）实际上是一个非平衡面板固定效应模型，但是文献[7]采取了基于上下楼集合将两个不同楼层的房产生成匹配对的方法来求解模型参数，存在匹配对选择不同计算出来的房价指数不同的问题。

将纵向非平衡面板模型（4）写成矩阵形式，记为：

2.2 固定效应面板模型的计算方法

式（7）的计算用到了QZμ=O，Qen=0。由Frish-Waugh-Lovell定理知式（6）关于β的最小二乘估计β̂与式（7）关于β的最小二乘估计β͂一样：

式（8）亦可看成由式（7）利用广义逆矩阵使用广义最小二乘法得到的计算公式。利用式（8）亦可设计出求固定效应μi的方法[10]。

2.3 随机效应面板模型的计算方法

若将式（6）中的μi看作固定效应，每一个上下楼集合对应一个μi，那么μi代表了该上下楼集合对房价带来的效应，在参数估计时自由度损失较大。如果将个体效应μi设定为随机的，即μi～N(0，σ2μ)，这时称式（6）为房价指数的纵向非平衡面板数据随机效应模型。

对于纵向非平衡面板数据随机效应模型，将其作为一个混合效应模型[10]来求解比用面板数据理论中的有关算法来求解更适合本文的情况，便于以统一的框架论述房价指数编制问题，以及扩展该模型。

在实际编制房价指数时，到底是选择纵向非平衡面板数据的固定效应模型还是随机效应模型，是一个较为理论化且复杂的问题。在统计学上选择面板数据的固定效应模型与随机效应模型时，往往使用Hausman 检验，根据统计量的P 值进行显著性判断。在选择房价指数编制模型时，除了上述一般性的方法外，还可以利用房价指数的经济学意义和回测误差来进行选择。

2.4 房价指数编制的评价方法

2.4.1 指数经济学意义的房价指数评价方法

一般而言，价格指数由样本数据经统计回归模型计算而得，样本数据的噪声不可避免地会出现在指数中。Guo等（2014）[3]针对两个或多个指数编制方法的比较问题，提出了两个数量指标：指数回报的标准差和1 阶自相关系数。这两个数量指标直接反映了指数回报的精确度。在其他情形相同的条件下，标准差越小、1 阶自相关系数越大，则指数就越准确，或者说指数中含有的噪声越小。Cocconcelli 和Medda 在分析宏观经济变量及房地产的价格序列时，提出用HP滤波设计数量指标来评价指数的光滑性。

式（10）第一部分是对波动部分的度量，第二部分是对趋势成分平滑程度的度量。λ（λ≥0）是平滑参数，用于调节两者的比例。分别对g1，g2，…，gn求导，并令导数等于0，容易解得趋势部分：

对于不同的房价指数模型所估计的指数序列，对应的dev的值越小，则指数质量越好。

2.4.2 均方根误差和平均绝对误差的评价方法

既然房价指数反映的是商品房价格的市场走势，那么用已经估计出来的房价指数去预测样本的房价，其预测房价与真实房价的差的大小可用来设计评价房价指数编制模型的优劣。

均方根误差（RMSE）如下：

平均绝对误差（MAE）如下：

其中，n为测试集中的个数，Yi和Ŷi分别为商品房i的实际价格和回测价格。

对于不同的模型，为计算RMSE 和MAE，首先由原始数据产生上下楼集合，产生模型要求的样本数据，进行参数的估计；然后，用计算的参数估计值进行每个样本的房价回测；最后，就可以按式（13）和式（14）进行计算。

对于纵向非平衡面板数据模型（4），利用样本数据集分别用固定效应和随机效应的计算方法估计模型（4）中房价指数参数和其他几个参数，得到各参数的估计值：β̂t(t=1，2，…，T)、α̂0、α̂1、α̂2、γ̂1、γ̂2、μ̂i(i=1，2，…，N)，其中μ̂i(i=1，2，…，N)是各个上下楼集合的固定效应的估计值或者随机效应的实际值。对于样本集中的第i个上下楼集合中的房产j，可得到其价格的预测值Ŷi，j：

而对于文献[8]中的模型（5），利用同样的样本数据集形成匹配对，估计相关参数。对样本集中的第i个上下楼集合中的房产j，找到第i个上下楼集合的另一个房产k的yi，k，利用其价格得到房产j的预测值Ŷi，j：

3 实证分析

本文从透明售房网（http：//tz.tmsf.com/）上获取的2015年1月至2019年12月包括浙江省台州市开发区、黄岩区、路桥区及椒江区的99 个楼盘的数万条网签数据，在剔除内容不完整的信息后，获得28552条有效样本信息。按照关于上下楼集合的要求，删除顶楼和一楼的样本后，至少还有两个样本。本文共得到2661 个上下楼集合，包含26869条数据。

3.1 固定效应和随机效应的计算结果

分别考虑模型（4）的个体为固定效应和随机效应，进行计算和显著性检验。当显著性水平为5%时，两种方法所有的系数都显著。对每个月对应的估计值β̂取自然底的幂，再乘以100即可得到相应月份的房价指数。为后续研究方便，将2015 年1 月作为基期，并设其房价指数为100。固定效应和随机效应面板模型计算的台州市2015—2019年部分月份的房价指数如下页表2中列（1）和列（2）所示。表2 中列（3）为按照文献[8]中模型计算的2015—2019年部分月份的房价指数。

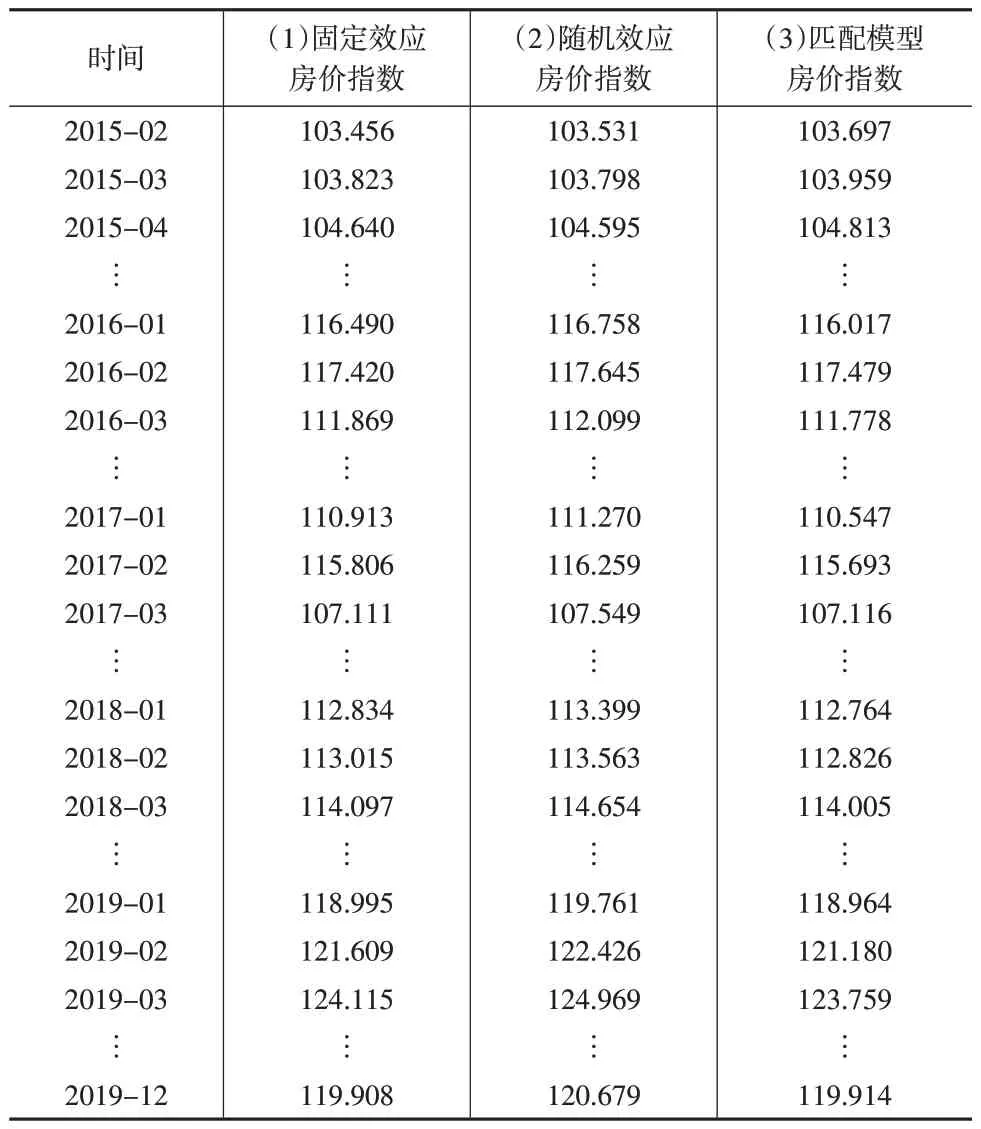
表2 纵向非平衡面板模型的计算结果

为了更加直观地比较三种模型计算的房价指数，利用表2中的数据绘制如下页图2所示的房价指数折线图。

从表2 和图2 可以看出，纵向非平衡面板数据模型的计算结果与文献[8]中对数匹配模型的结果总体上相近。由于所选样本中房屋类型主要是小高层和高层，将同一上下楼集合中的房产进行匹配和将其看成整体进行计算没有太大差别。对本文的样本数据来说，纵向非平衡面板数据固定效应模型与随机效应模型的计算结果非常接近。

3.2 评价结果

用式（9）和式（12）进行评价指标的计算，得到如表3所示的结果。由于本文采用的数据是月度数据，用式（10）进行计算时，取λ=14400。

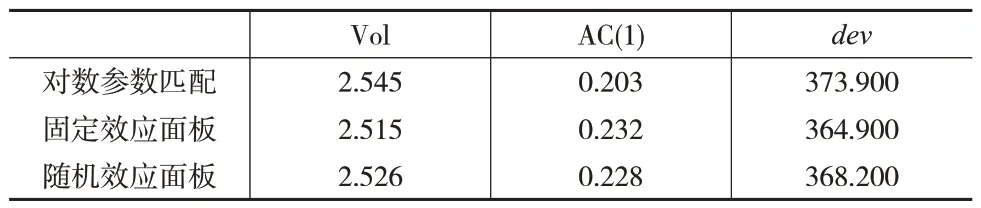
表3 3种模型的评价指标的值

从表3 中3 个指标的计算结果可以看出，纵向非平衡面板数据固定效应模型的表现比对数参数匹配模型要好很多，比纵向非平衡面板数据随机效应模型也要稍好一些。

同样以2015 年1 月至2019 年12 月台州市开发区、黄岩区、路桥区及椒江区的99 个楼盘的数万条网签数据为例，对以上3个模型进行比较分析。用式（13）和式（14）计算可得每个模型对应的RMSE和MAE，如表4所示。

表4 3种模型的误差

从表4可以看出，总体上面板数据模型比参数匹配模型的RMSE 和MAE 要小很多，说明使用面板数据模型有一定的优势。对于本文实证分析采用的数据来说，纵向非平衡面板数据固定效应模型相较于随机效应模型只有微小的改进，区别几乎不大。在具体应用时，应针对不同城市的实际数据，应用上述方法进行比较，选定相对较优的模型，进行新建普通住宅房价指数的编制与发布。

4 结束语

针对现有的特征价格法、重复交易法及样本匹配法在特征变量选取、样本选择缺乏代表性及同一上下楼集合的房产以不同顺序组成匹配对所产生的理论问题与计算问题，本文在房价指数的编制过程中将上下楼集合中的所有交易房产看作一个整体来研究，构建了纵向非平衡面板模型。对于纵向非平衡面板数据固定效应模型，给出了消除组内共同项的回归方法。对于纵向非平衡面板随机效应模型，通过将纵向非平衡数据模型化为一个混合效应模型，给出了计算房价指数的方法。此外，还设计了模型评价方法，为研究房价指数编制选定模型与计算方法提供了量化标准。随着我国房地产市场的成熟和完善，可以预见二手普通住宅和新建普通住宅在房屋结构等方面的差距会逐渐缩小，由于历史原因暂时分开的两个住宅市场将会合并进而编制一个统一的房价指数。从本文的论述和计算结果可以看出，几乎不需要做太大的改动，就可用纵向非平衡面板模型来编制二手房市场与新建房市场合并后的统一的房价指数。