带流数据集AFT模型的可再生估计

潘莹丽，黄 河

（1.湖北大学a.数学与统计学学院；b.应用数学湖北省重点实验室，武汉 430062；2.梧州学院 管理学院，广西 梧州 543002)

0 引言

基于右删失生存数据分析协变量与生存时间的相关性时，应用最广泛的统计模型之一是加速失效时间模型（AFT模型）[1—5]，然而相关研究大多是基于存储到磁盘的静态数据进行的。由于现代很多功能强大的计算平台的应用广泛，有关生存分析中流数据的统计分析在大数据领域频繁出现。生存分析中的流数据又称为实时大数据，是一组连续的、海量的、快速的、连续到达的数据序列，其突出特点是“实时到达、速率多变、连续到达、次序独立；规模宏大，有不可预测的极值；数据一旦被处理，除非经过特别保存，否则不能取出来再次使用，或者再次提取数据的成本很高”。由于这些独有的特征，因此依靠传统的数据挖掘技术和方法很难实时获取流数据中承载的重要信息和进行复杂的计算。基于流数据集的统计分析方法有很多，当优化问题具有封闭形式的表达式时，Schifano等（2016）[6]提出可以直接通过对数据集的递归过程来更新估计量。封闭形式的表达式在实际应用中并不经常存在。Robbins和Monro（1951）[7]提出一种梯度下降算法（SGD），然而SGD算法对学习速率非常敏感。为了解决这一问题，Toulis 等（2014）[8]提出了隐式SGD 算法和平均隐式SGD 算法。此外，一些学者还提出了在线二阶算法来处理流数据[9]。为了保证估计量的一致性，基于SGD的方法和在线二阶算法需要对数据集进行较强的约束假设。为了避免约束假设，在可再生广义线性回归的研究中，Luo和Song（2020）[10]采用构造在线更新估计方程的方法，实现了对模型的在线统计推断。在可再生分位数回归研究中，Wang等（2022）[11]通过构造在线更新似然函数，仅使用前期数据的统计量和当前批数据对提出的估计量实现了在线更新；在可再生参数、半参数和非参数模型研究中，Lin等（2020）[12]建立了针对流数据集的在线更新估计方法。然而，这些研究全部基于完全观测的流数据。

对于流数据分析的架构，Warren和Marz（2015）[13]提出了一种Lambda 架构。Lambda 架构是一个实时的大数据计算和存储系统，由速度层、批处理层和服务层组成。通过使用增量算法在速度层捕获瞬时的实时视图，并且更新先前存储的视图，而批处理层存储不断增长的数据，并在新的数据批次到达时不断重新计算批处理视图，从而细化在速度层产生的无法保证估计准确性的结果。批处理层和速度层输出的视图被存储在服务层中用于查询。这种架构非常灵活，但是却完全忽略了实时统计推断的需要。Luo和Song（2020）[10]提出添加一个新的推理层来扩展Lambda架构中的速度层，并将这种新架构命名为rho架构，从而对流数据进行统计推断。基于AFT模型，本文采用构造在线更新估计方程的思想构造可再生估计并引用rho架构，提出一种新的基于AFT模型的可再生估计的流数据分析策略，这种策略仅使用当前批数据和历史批数据的汇总统计来更新估计量，解决了流数据集量大无法被全部保存的问题。提出的流数据分析策略，在计算上是高效的，有利于流数据的存储和算法的加速，也不会损失任何估计效率。

1 模型和可再生估计

1.1 带流数据集的AFT模型

其中，β=( )β1，β2，…，βp为p维待估参数，ε是误差项。将观测时间y1，y2，…，ynk按从小到大的顺序排列，得到yi的次序统计量y(1)≤y(2)≤…≤y(nk)。设δ(1)，δ(2)，…，δ(nk)为y(1)，y(2)，…，y(nk)的相应右删失变量，x(1)，x(2)，…,x(nk)为相应的协变量。为了处理数据删失带来的信息不完整性，基于第k批数据，根据Stute 和Wang（1993）[14]的研究，构造权重ω(1)，ω(2)，…，ω(nk)，其中ω(i)可以表示为：

1.2 可再生估计

由上述推导过程知，估计量β͂2和β̂2*是近似等价的，通过求解式（9），初始值β̂1就可以更新为β͂2。从数值上讲，通过牛顿-拉夫逊迭代算法可以得到β͂2的值，即β͂2的第r+1次迭代为：

本文绘制了可再生过程rho结构流程图（见图1）。

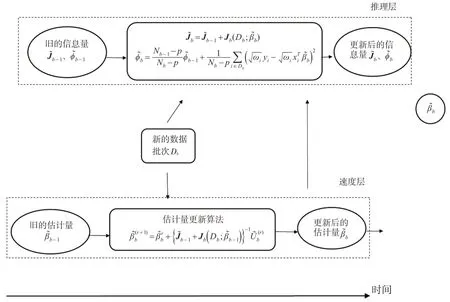
图1 rho结构流程图

通过流程图1，设计可再生估计更新算法（见算法1）。

算法1：基于AFT模型的可再生估计算法。

（1）输入：流数据集D1，D2，…，Db，…。

（2）输出：β͂b和V͂ar(β͂b)，其中b=1，2，…。

（3）初始化：β͂init，φ͂0=0，J͂0=0p×p。

（4）forb=1，2，…do。

（5）读取流数据集Db。

（10）释放数据集Db。

（11）end。

（12）返回β͂b和V͂ar(β͂b)，forb=1，2，…。

算法解读如下：

（1）第一行：所有流数据集都来自真实参数为β0的AFT模型。

（2）第二行：输出数据包括每个批次b的β的可再生估计值和估计的渐近方差。

（3）第三行：为β0设置初始值，比如β͂init=0。

（4）第四行：根据数据流运行在线更新过程。

（5）第六行：在推理层，计算负Hessian 矩阵Jb(Db;β͂b-1)并与速度层通信。

（6）第七行：在速度层，运行更新算法，将β͂b-1更新为β͂b。

（7）第八行：在推理层，根据新的数据批次Db和加速层更新后的β͂b，更新负Hessian矩阵J͂b和估计量φ͂b。

2 数值模拟

本文通过数值模拟评估带流数据集的AFT 模型的可再生估计方法在有限样本中的性能，并将其与基于整个数据集计算的Oracle 方法进行比较。采用如下四个指标来评估不同方法的性能：参数估计的偏差Bias（即参数估计值的均值与参数真实值的差）、估计值的样本标准差SD、估计值的标准误差SE和95%正态置信区间的经验覆盖率CP。对于第k（k=1，2，…，b）批数据中的第i个个体，假设生存时间Ti由以下模型生成：

2.1 固定总样本量Nb，变化每批样本量nk

固定样本量Nb=100000，每批样本量nk分别取500、800、1000 和2000，表1 汇总了(β1，β2)=(-0.500，0.693)的模拟结果，表2 汇总了(β1，β2)=(0.500，-0.693)的模拟结果。

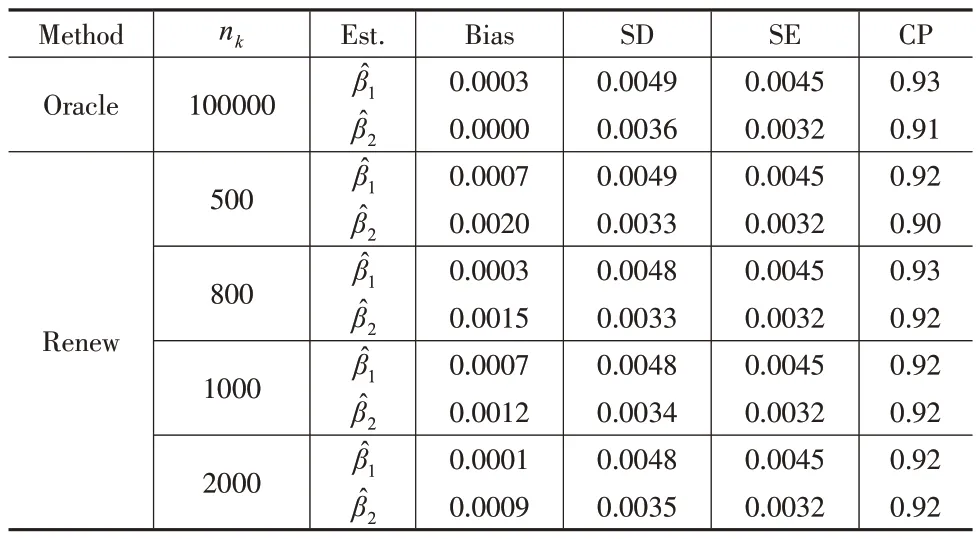
表1 固定Nb=100000，变化nk 时的模拟结果（( β1，β2 )=(-0.500，0.693)）

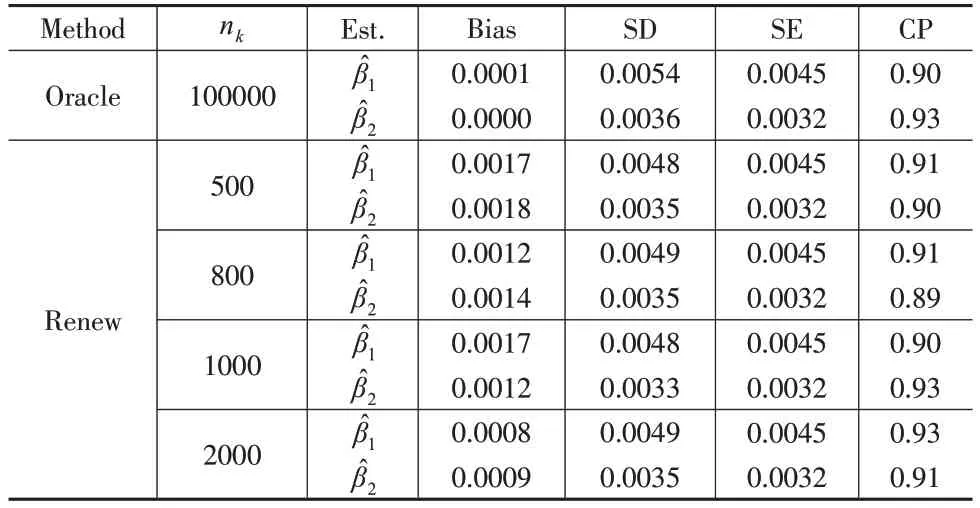
表2 固定Nb=100000，变化nk 时的模拟结果（β1，β2=(0.500，-0.693)）

2.2 固定每批样本量nk，变化总样本量Nb

固定每一批次的样本量nk=100，总样本量Nb分别取值1000、5000、8000和10000，表3汇总了(β1，β2)=(-0.500，0.693)的模拟结果，表4汇总了(β1，β2)=(0.500，-0.693)的模拟结果。

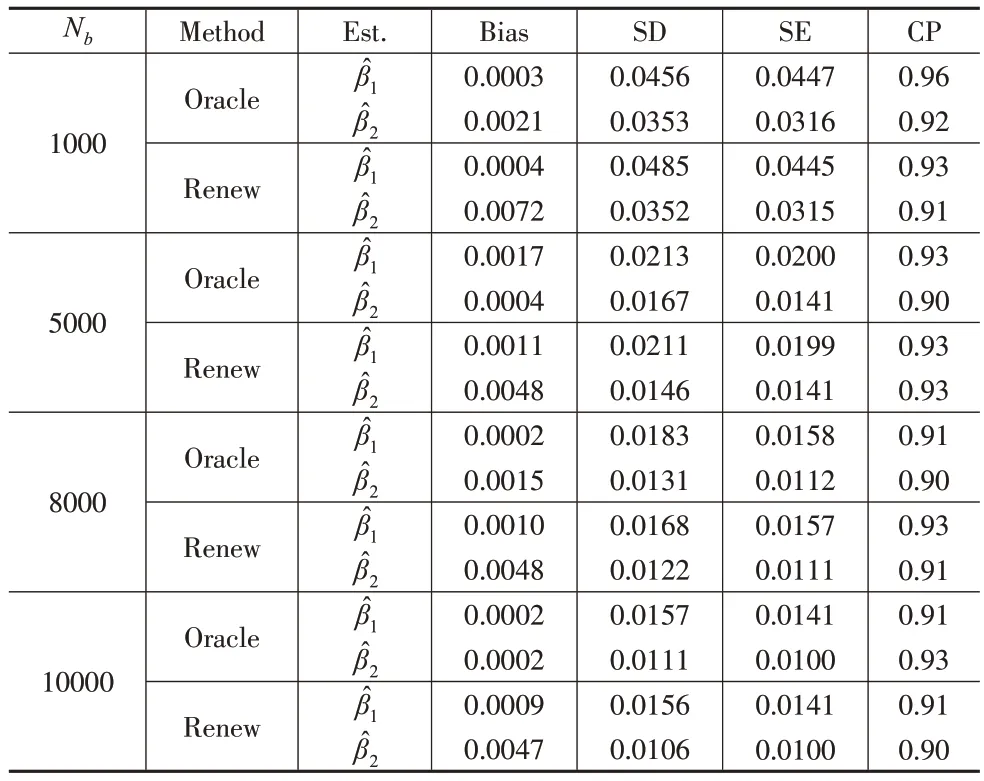
表3 固定nk=100，变化Nb 时的模拟结果（( β1，β2 )=(-0.500，0.693)）

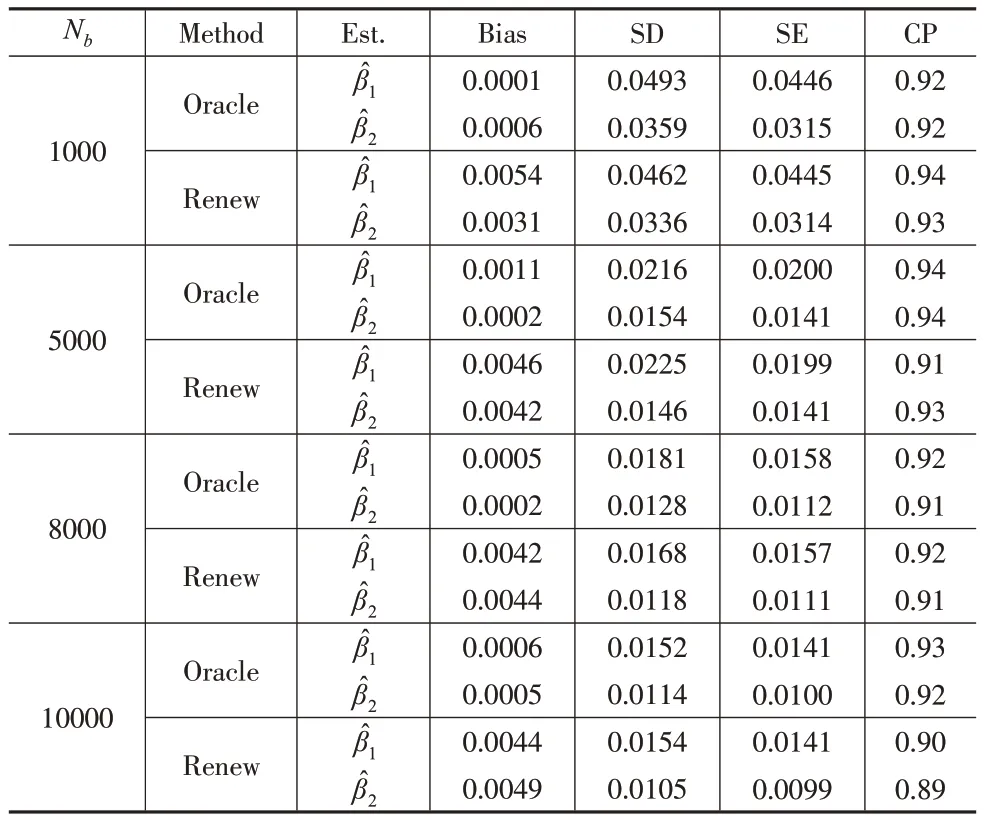
表4 固定nk=100，变化Nb 时的模拟结果（( β1，β2 )=(0.500，-0.693)）

综合比较表1至表4中的结果，可以得出以下结论：

（1）本文提出的可再生方法得到的估计值与Oracle方法可以相比较，偏差Bias接近于0，说明β1和β2的估计量是近似无偏的，而标准误差SE和估计值的样本标准差SD几乎相同，说明估计的标准误差为估计值的样本标准差提供了较为良好的估计，此外覆盖率CP也几乎都在90%附近。

（2）固定总样本量Nb=100000 保持不变，偏差Bias、估计值的样本标准差SD 和标准误差SE 随着每一批次样本量nk的增加几乎保持不变，说明提出的可再生估计量的估计结果几乎不受每一批次样本量nk大小的影响。

（3）固定每一批次样本量nk=100 保持不变，随着批次从10 增加到100，总样本量从1000 累积到了10000，可再生方法的标准差SD 和标准误差SE 的值都在一定程度上有所减小，说明可再生方法的性能越来越好。此外，在这种情况下的模拟结果也证实了本文提出的更新方法对于数据批次是稳健的。

3 实例

为了进一步证明本文提出的可再生估计方法的可操作性和有效性，将提出的方法应用于华盛顿大学Diana 等提供的单芽插条萌芽真实数据集中。该数据集的观察期为2013—2016 年，在此期间，霞多丽（CH）和赤霞珠（CS）这两个品种的芽从8月开始每周采样一次，到12月第一周结束。在前三年中，每个样品使用了18个插条，最后一年使用了30个插条。将插条放置在装满潮湿砂基材的铝托盘上。将托盘置于生长室中，在24±2°C 的温度下，光照15 小时。每两天观察一次插条，记录萌芽的持续时间。该数据集包含总样本量N=3288，将数据分成b=24 个批次来模拟一个动态过程，每个批次包含的样本量为nk=137，这种模拟动态过程的分割策略在在线流数据的研究中被广泛使用。

在分析中，考虑两个潜在的协变量：品种（x1）和样本的切割数量（x2）。本文最终关心的结果是萌芽持续的时间，其删失率约为12.1%。考虑如下AFT模型来评估上述两个变量对萌芽持续时间T的影响：

log(T)=β1x1+β2x2

类似于模拟研究，将提出的可再生估计方法与Oracle方法进行比较。表5 汇总了参数估计（Est.），标准误差（SE）和P 值（P-values）。从表5 可以看出，本文提出的方法得出协变量x1和x2对萌芽持续时间都具有显著影响。对于协变量x2，Oracle方法和本文提出的方法均显示对萌芽持续时间具有显著影响。

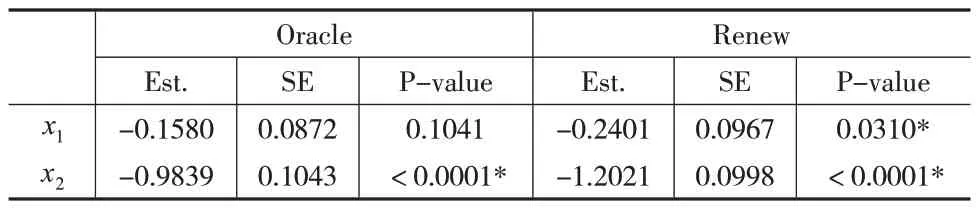
表5 实证结果

4 结束语

本文基于带有流数据集的AFT模型，通过构造在线更新估计方程的方法，提出仅基于前期数据统计量和当前批数据的可再生估计，研究了一种基于AFT模型的流数据分析策略，有效解决了计算机存储瓶颈的问题。模拟研究展示了所提出方法在有限样本量下的优良表现；实际数据分析展示了所提出方法的有效性与实用性。当每批右删失流数据的样本量非常大时，研究的主要预算和成本来自昂贵的重要协变量的测量，在有限的时间或预算下，观测每批研究对象的昂贵协变量往往不可行。因此，基于AFT模型，未来继续研究Case-Cohort 设计[15]、广义的Case-Cohort设计[16]、Outcome-Dependent Sampling（ODS）设计[17]等有偏抽样设计下右删失流数据的建模、统计推断、实时计算等将非常有意义。