一种解决三区间数回归的混合PM方法

汪 瑜，林祎明，孙慧敏

（中国民用航空飞行学院 经济与管理学院，四川 广汉 618307）

0 引言

线性回归是指利用数理统计中的回归分析确定被解释变量和两个或者两个以上解释变量之间线性关系的一种统计分析方法。在大数据时代，大量精确点数据被压缩和归类到若干具备上下界的区间中，并通常会在该类区间中增加一个最有可能值，以防止因数据压缩而造成的信息过度丢失现象。正是这种优势使得三区间数被广泛应用于交通、医药、金融、工程等领域。三区间线性回归就是探索这种三区间数据类型变量之间相互依赖关系的一种方法，且被广泛应用于模式识别、人工智能、数据挖掘、数据建模等领域。

区间回归法从区间数据中利用不同的参考点对被解释变量进行回归预测。现有的区间回归法大多选取区间中点范围或者端点作为参考点展开研究[1—4]。Billard和Diday（2000）[5]首先提出了中点法（Center Method，CM），通过区间数据的中点对回归系数进行求解，进而推导出回归区间的上下界。Neto和Carvalho（2008）[6]提出了中点范围法（Centre and Range Method，CRM），通过区间数据的中点和范围来对被解释变量的上下界进行回归预测。然而，上述回归方法均不能保证区间的数学一致性。为了解决上述问题，Lima和Carvalho（2010）[7]提出了一种考虑增加范围系数非负约束的CRM 法，即CCRM（Constrained Center and Range Method）法来保证回归区间的合理性。Dias和Brito（2017）[8]提出了一种用分位数函数表示区间分布的回归模型（ID模型），并对回归参数进行非负约束以保证数学一致性，但该模型仅在被解释变量与解释变量之间存在正相关关系时才会起作用。Zhao等（2022）[9]提出了一种基于中点和对数范围的区间值数据稳健回归方法（LN-IRR），并分别建立了基于区间变量的中点和区间对数范围的回归模型，该模型针对对数范围建模，可以消除区间范围上的非负约束。Giordani（2011）[10]提出了一种更加灵活的Lasso-IR线性回归方法，该方法使用了最小绝对收缩和选择算子（Lasso）约束，并对区间值数据的中点和半径进行线性回归分析，然而该方法假设被解释变量的回归半径（中点）只依赖于解释变量的半径（中点），不存在任何的交叉关系。Billard 和Diday（2002）[11]提出了基于解释变量区间数据上下界进行回归预测的最大最小值法（MinMax Method，MinMax），相较于中点范围法，仅选取端点作为参考点无法体现数据的内部波动情况进而使得数据信息过度丢失，因此部分学者基于区间端点进行改进研究。为了减少数据信息的丢失，Wang等（2012）[12]提出了一种捕捉区间值观测的完整信息的线性模型，称为完全信息方法（Complete Information Method，CIM）。Nasirzadeh等（2021）[13]为了增加数据信息的可利用度，提出了一种在观测区间上下界内均匀选取参考点从而分别建立回归上下界的方法，称为马尔可夫链蒙特卡洛方法（MCMC）。Baymani和Saffaran（2021）[14]在传统ε-SVR方法的基础上提出一种ISVR（Interval Support Vector Regression）方法，该方法利用区间数据的下界和上界解决了两个ε-SVR问题从而得到两个超平面。通过实例验证发现，相较于ε-SVR方法，ISVR方法对于数据集中的样本数量是没有限制的，且实验效果优于CM、CRM和CCRM方法。可以发现，现有的中点范围法和端点法都是选取固定参考点来进行回归，但在观测数据波动较大时，这种固定参考点的回归方法往往效果不佳。为了解决这一问题，Souza 等（2017）[15]提出了一种PM（Parameterized Method）方法，该模型通过自动调整区间上下界的被选择参考点来优化回归效果，同时CM、MINMAX和CRM方法均被证明是PM方法的特殊形式。但该模型在区间数据波动幅度过大时，却很难解决区间的相交性问题。另外，上述区间回归法大多仅针对具有上下界的两区间数据格式，因此无法直接用于解决三区间数的回归问题。

鉴于此，本文首先将区间上下界数据序列用参数化方法表示，将最有可能值数据序列用普通点回归模型表示；其次，通过限制“回归区间上界≥回归最有可能值点≥回归区间下界”来保证区间数据的数学一致性，并增加“回归区间上界≥观测区间下界且观测区间上界≥回归区间下界”这一约束条件来保证区间的相交性，从而构建以被解释变量回归区间与观测区间上下界误差值和最有可能值误差值平方和最小化为目标函数的区间回归模型；再次，基于K-T条件对模型的回归系数进行讨论和求解；最后，通过蒙特卡洛模拟法检验本文模型的优势。

1 三区间数回归的混合PM方法

1.1 上下界回归的PM模型

上下界的区间回归PM 模型本质上是两区间数回归PM模型。该模型通过自动调整区间上下界被选择参考点来实现优化回归误差的目的。下页图1 是以回归下界为例展示的PM方法的基本原理。

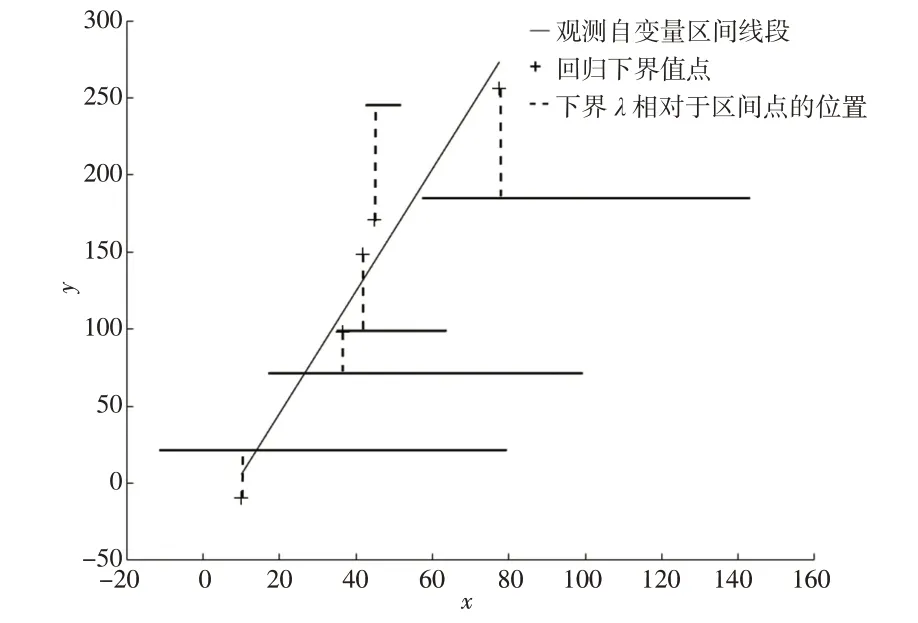
图1 PM方法的基本原理

可以发现，PM方法通过自动调整固定参考点（即每一个自变量的观测下界线段的固定分配比例）的选择来达到优化回归误差的目的。但现有的PM 方法只通过限定每个回归区间的非负性来保证区间数据的数学一致性。当区间数据整体波动过大时，可能会出现回归精度下降的现象（如下页图2所示），无法保证区间的相交性。

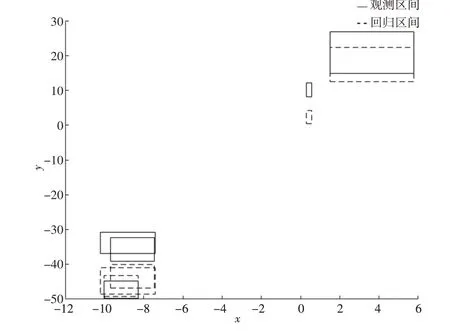
图2 区间数据波动幅度过大时的PM方法回归效果图

尤其是对于三区间数回归问题，目前的两区间数回归的PM法无法保证最有可能值、上下界之间的数学一致性，同时也无法确保三区间观测区间和回归区间的相交性。

1.2 最有可能值的回归模型

基于CRM 方法[6]的基本理念对最有可能值点进行建模，如式（3）所示：

1.3 三区间数回归的混合PM模型

由于本文增加了最有可能值点，因此为了使混合模型的回归精度最大化，将目标函数定义为被解释变量上界、下界和最有可能值点误差项的平方和最小化，具体如式（6）所示：

由图2 可知，该模型在区间数据波动幅度较大时难以保证回归区间与观测区间一定存在交集，进而导致模型的回归精度降低，因此需要对PM模型进行改进。为保证回归区间和观测区间的相交性，添加如下两条约束：（1）回归区间上界≥观测区间下界；（2）观测区间上界≥回归区间下界。具体模型如式（7）和式（8）所示，称为PM+模型。

1.4 回归系数求解

为了便于系数估计值的求解，将上述模型转化为矩阵形式，如式（9）所示：

将式（10）中的约束条件转化为式（11）的形式，可知该模型的约束条件均为线性函数，因此其Hessian矩阵均为实对称矩阵，且他们的各阶主子式均为0，因此约束条件均为凹函数。

表1 解的可能性的情况讨论

1.5 评价指标

现有两区间PM 模型通常选取均方根误差（RMSE）、平均准确率（AR）、平均比率（PCO）[15]和观测区间与回归区间不相交的个数（N0）[16]四个方面的评价指标对模型的回归结果进行比较。在解决三区间数问题时，本文在上述基础上进行扩展。

（1）RMSE

为了明确三区间混合回归模型对区间数据每一部分的回归精度的影响，本文主要从观测区间与回归区间的左半径均方根误差（RMSErl）、右半径均方根误差（RMSErr）、最有可能值均方根误差（RMSEm）和整体均方根误差（RMSE）四个方面来计算。

（2）AR

对于AR 来说，本文主要从左半径平均准确率（ARrl）和右半径平均准确率（ARrr）两个方面来计算。

2 蒙特卡洛模拟分析

为了验证本文PM+模型的优势，将其与文献[2]和[16]中的CCRM+模型进行对比分析。

2.1 模拟数据生成

为了便于对比，本文采用前文选取的评价指标进行计算分析；为了说明区间自变量个数对于回归效果的影响，本文分别模拟了自变量个数j=1 和j=3 两种情况；为了说明数据波动幅度对回归模型精度的影响，本文分别模拟了中点序列和范围序列两种不同的波动情况来进行对比分析。

在蒙特卡洛模拟过程中，本文基于CRM模型[6]的基本思想共生成了400组数据，其中的300组数据作为训练集，用于回归系数的估计；其余100 组数据作为测试集，用于对回归结果进行评价。为了避免1次模拟的随机性，本文对上述过程重复100次，结果如表2所示。

表2 蒙特卡洛模拟过程的数据生成

2.2 结果对比与分析

本文通过t 检验对改进的CCRM模型（简称CCRM+模型）和PM+模型进行比较，显著性水平取为1%。将CCRM+模型优于PM+模型作为原假设，将CCRM+模型不劣于PM+模型作为备择假设。考虑到RMSE为成本型指标，该指标值越大说明拟合的效果越差，因此原假设为RMSECCRM+＜RMSEPM+，备择假设为RMSECCRM+≥RMSEPM+；考虑到AR和PCO 为效益型指标，该指标值越大说明拟合的效果越好，因此原假设为PCOCCRM+＞PCOPM+时，备择假设为PCOCCRM+≤PCOPM+；原假设为ARCCRM+＞ARPM+时，备择假设为ARCCRM+≤ARPM+。若假设CCRM+模型和PM+模型相同，则原假设为CCRM+模型与PM+模型的指标值相同，备择假设为CCRM+模型与PM+模型的指标值不相同。

表3 至表5 分别是以CCRM+模型优于、劣于、等同于PM+模型作为原假设进行t检验的结果。

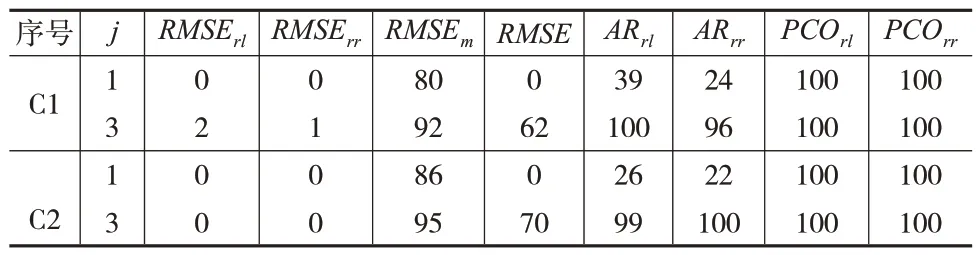
表3 CCRM+模型优于PM+模型为原假设 （单位：%）

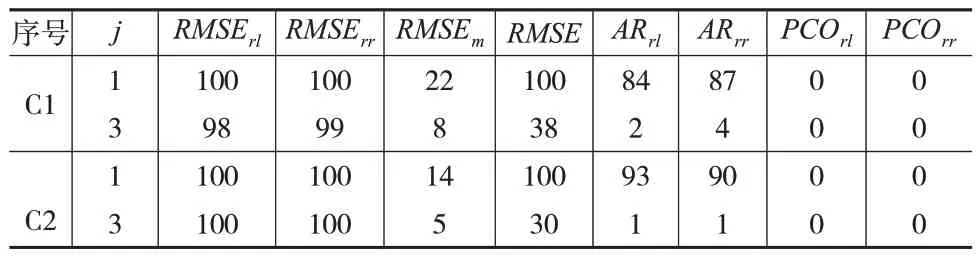
表4 CCRM+模型劣于PM+模型为原假设 （单位：%）

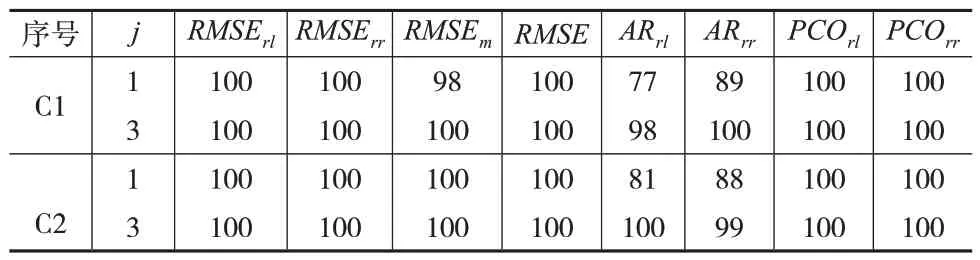
表5 CCRM+模型等同于PM+模型为原假设 （单位：%）

可以看出：均方根误差RMSErl和RMSErr均拒绝“CCRM+模型劣于PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型优于PM+模型”的原假设。RMSEm拒绝“CCRM+模型优于PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型劣于PM+模型”的原假设。当j=1时，RMSE拒绝“CCRM+模型劣于PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型优于PM+模型”的原假设；当j=3 时，RMSE拒绝“CCRM+模型优于PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型劣于PM+模型”的原假设。

观测区间包含预测区间的平均比率PCOrl和PCOrr均拒绝“CCRM+模型优PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型劣于PM+模型”的原假设。

在j=1 的情形下，平均准确率ARrl和ARrr均拒绝“CCRM+模型劣于PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型优于PM+模型”的原假设。在j=3 的情形下，ARrl和ARrr均拒绝“CCRM+模型优于PM+模型”和“CCRM+模型等同于PM+模型”的原假设，但接受“CCRM+模型劣于PM+模型”的原假设。

综上所述，相较于CCRM+模型，PM+模型的回归精度明显提高，但却是以牺牲一部分的均方根误差和平均准确率的拟合精度为代价的。此外，随着数据波动幅度和解释变量个数的增加，PM+模型只牺牲了较小的RMSErl和RMSErr值就保证了整体的回归精度，具有明显的优势。

表6给出了100组测试数据下各类评价指标的均值。

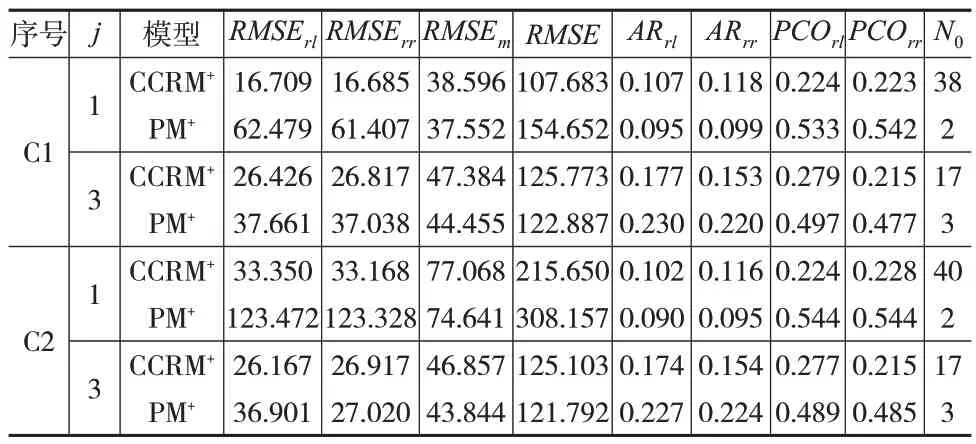
表6 CCRM+模型与PM+模型评价指标值

可以发现，对于均方根误差来说，相较于j=1 的情形，j=3 情形下PM+模型均方根误差的相关指标值的牺牲较小，在RMSEm和RMSE方面均优于CCRM+模型的拟合精度，且在多元拟合下两个模型在RMSErl和RMSErr指标方面的差距明显缩小，说明此时PM+模型在RMSErl和RMSErr方面也有一定程度的改善。对于平均准确率来说，当j=1 时，PM+模型的指标值在整体上略小于CCRM+模型的指标值，在多元回归的情况下，随着区间数据序列波动幅度增大，PM+模型的AR 值有所提高且大于CCRM+模型的AR 值。此外，PM+模型的PCOrl、PCOrr和N0指标明显优于CCRM+模型，即使在数据波动幅度较大时仍能保持在较高的水平，说明PM+模型的回归精度明显高于CCRM+模型且在极大程度上保证了回归区间和观测区间的重合度。相较于CCRM+模型选取固定的中点和范围作为参考点，PM+模型通过自动调整λlj和λuj值获得使目标函数取得最小值的回归系数这一方法使得最终的回归精度明显提高。

3 结论

三区间数线性回归是数据建模分析中的一类重要问题，具有广泛的应用价值。本文在两区间数PM回归模型的基础上，将区间上下界数据序列用参数化方法表示，将最有可能值数据序列用普通点回归模型表示，然后以被解释变量回归上下界和最有可能值误差平方和最小化为目标函数，以保证区间数据的数学一致性和观测区间与回归区间必存在交集为约束条件，提出了三区间数回归的混合PM模型。蒙特卡洛模拟结果验证了本文的PM+模型能够提升区间回归精度，尤其是在PCO 和N0方面具有明显优势，且该模型无论是在一元回归还是多元回归过程中都保持着较好的回归效果。需要说明的是，该模型的总体回归效果是以牺牲一小部分RMSE 或者AR 值为代价的，因此如何平衡这种关系是后续研究的一个重要方向。