某医疗器械生产企业的维保工程多项目资源优化

王需凯

上海理工大学管理学院 （上海 200093 ）

随着国家医保覆盖范围的扩大、医保给付比例的提高及企业产品竞争力的持续提升，某医疗器械生产企业近十年的销售业绩快速增长，公司内部支持部门的工作均围绕销售工作展开。售后服务部门为配合销售部门的工作，需配置相应的维保人员和专业设备及时保障维保工程多项目同时推进。销售业绩快速增长时期，企业利润大量增加，对配置维保人员和专业设备的审核相对宽松，维保工程所需人员和设备资源较为充足。但近年来国家不断深化医疗改革，并收紧医保控费，医疗器械生产企业的利润逐渐下降，对成本控制的要求不断提升。这种情况下，企业为降低经营成本，需要控制不直接产生利润的相关业务成本，严格管控售后服务部门的维保人员和专业设备配置需求。这直接导致维保人力和专业设备的增速慢于维保任务增速。而项目管理人员并没有迅速适应这个变化并及时做出调整，依然按照之前资源充足时的工作习惯进行项目管理工作，缺少资源平衡意识和相关技术手段，进而导致资源负荷整体波动较大。随着资源负荷波动的进一步加剧，该企业的维保工程多项目管理工作出现了资源需求波动过大、项目资源冲突导致的无法按时完工问题，维保工程多项目同步推进遇到了挑战。为解决以上问题，本研究提出了一种资源优化方案，以期最大化利用有限资源助力企业发展。

1 某医疗器械生产企业维保工程多项目管理中存在的主要问题

为了解目前该企业维保工程多项目管理中存在的主要问题，我们在得到企业管理层的许可后，对其维保工程多项目管理现状进行了调查。调查主要采用与26 位维保工程项目管理员工访谈的形式。通过对访谈内容进行整理，我们发现该企业的维保工程特点和存在的主要问题如下。

该企业维保工程的开展场所是医疗机构。由于医疗机构工作时间的特殊性，多数医疗器械周一至周六早7 点至晚7 点均处于使用状态，部分器械甚至需要使用至晚11 点左右。因此，除故障维修工作可以随时开展外，巡检、保养、大修等维保工作必须在晚间或周日进行，且需要提前与使用科室预约。这大大限制了维保工程的作业时间，对于资源的调配、进度的安排提出了更高的要求。

新型冠状病毒感染疫情期间，在出行受限、现场突发情况增加及时间、人力、零配件、关键设备资源受限等因素的影响下，维保工程多项目推进难度增加，项目之间资源冲突加剧，项目延期问题逐渐凸显，从而影响了整体完工时间，导致客户满意度下降、客户投诉量上升及销售团队满意度下降，影响了企业的长远发展。目前，维保工程多项目管理中最主要的问题是进度安排不合理导致资源负荷波动较大，降低了应对突发事件的能力，进一步增加了项目冲突的可能性[1]。

由于维保工程的特殊性，巡检和保养周期较为固定，且浮动时间较短，必然会导致不同月份之间资源负荷波动较大。但根据调查反馈，多项目管理中同1 个月的不同周之间资源负荷波动依然较大。虽然医疗器械维保工程常会出现突发工作，且存在由于合同签定日期不同导致各项工作开展日期无法在较长时间内确定等情况，但该资源负荷波动问题会进一步导致在资源紧张时出现资源冲突及加班赶工等增加项目费用的情况，或者在资源需求低谷时出现资源积压和资源浪费的情况。

2 资源优化方案

2.1 优化目标和方法

考虑到该企业在一段固定时期（1 个月）内新导入项目较少，对维保工作量的预估相对准确，可在该时期对多项目进行相对准确的网络计划编制，从而为开展资源平衡工作提供基础。因此，本研究以月为单位开展资源优化工作。由于医疗器械维保工程的特殊性，维保合同约定的工期通常是固定的，因此资源优化目标可转化为固定工期下的资源平衡工作，即在不考虑瓶颈资源且保持工期固定的前提下，通过调整非关键链上活动的进度使资源需求量随着时间的推进保持相对平稳[2]。由于项目非关键链上的活动可以在网络计划中的最早开始时间和最晚开始时间范围内的任意1 天开始，因此通过调整非关键链上活动的开始时间即可改善资源平衡状况。

为了使多项目资源平衡问题具有可操作性，本研究将多项目的资源平衡问题转化为单项目的资源平衡问题进行研究[3]，即将多个项目合并成为一个大项目，将多个单代号网络图连接成一个较大的单代号网络图，从而实现多项目进度管理向单项目进度管理的转换。而在多项目管理中，每个项目的开始时间和结束时间不可能完全一致，因此需要在合并每个项目单代号网络图关键路线上首尾各添加一个辅助活动，这些辅助活动可以设置持续时间（也可以为零），但占用资源为零，所有的起始辅助活动和结束辅助活动各自共用一个节点，从而将多个单代号网络图连接成一个单代号网络图。使用单位为天的实际资源负荷量与工期内平均资源负荷的方差为平衡指标，通过调整各活动的开始时间来缩小方差。将该数学模型作为资源平衡的目标函数[2]。

由于多项目网络计划是一个复杂、离散的组合优化问题，而遗传算法在处理离散优化搜索问题方面具有独到的优势，其不仅不需要求解空间的连续性，也不需要任何梯度信息，其适应性已经在处理大型复杂优化问题上得到了验证。因此，本研究采用遗传算法对多项目资源优化的数学模型进行求解[4]。

2.2 优化步骤

2.2.1 多项目网络计划转化为单个项目网络计划

假定A={1，2，…，M}为项目集，项目m 活动集合为{1，2，…，Im}，项目工期为Tm，开始时间为Sm，首尾添加的辅助活动分别为ms和mg。开始时间 {Sm}，n∈［1，M］。合并后的工期T=max{Sm+Tm}-S，m∈［1，M］。项目m 的辅助活动ms的开始时间Sms=S,持续时间dms=Sm-S，辅助活动mg的完成时间Fmg=T+S，持续时间dmg=（S+T）-（Sm+Tm）。合并后的活动集C={1，2，…，n}，n=I1+I2+…+IM。至此，多项目的多个网络计划转换为了一个网络计划，为解决多项目资源平衡问题奠定了基础。

2.2.2 优化数学模型的确定

优化目标的数学模型为：

式中，rj（t）表示在第t天对资源j的需求量；im代表第m个项目中的第i个活动，im∈（1，Im）；Im为第m个项目总的活动数量；rj，im（t）为对于对资源j，第m个项目中活动i在第t天的需求总量，m∈（1，M）。r-j表示资源j在整个工期内的日均需求量。

假定每一个活动的资源需求量固定且可事先确定，那么在整个工期中的某1 天，活动im对资源需求情况rj，im（t）有且只有两种可能：固定的资源强度rj，im和零（该活动在第t天未被执行）。其中，ASim和AFim分别为活动im的实际开始时间和实际结束时间。以上描述的数学模型表示如下：

3 遗传算法的选择和应用

本研究采用MATLAB 遗传算法工具箱与直接搜索工具箱GADS，通过编写目标函数表达式并设置相关参数（调用GUI 界面并在相应参数的位置上输入特定值或使用默认值）对模型进行求解。另外，需要注意的是，GADS 是对目标函数取最小值进行优化，求解最大值时需将适应度函数乘以-1。

根据该企业维保工程项目的特点及多项目管理架构，选择S 省区对前文确定的资源优化方案进行效果验证。验证方法为：统计S 省区使用该优化方案前后的资源负荷波动情况并对比。因保密性要求不便在文中展示全部数据，现选取优化期间的2 个包含大修工程项目的大修加保养工作模块作为算例用于展示计算过程。

3.1 多项目网络计划转化为单一网络计划

本研究选取的2 个项目阶段性工作的单代号网络见图1 和图2。

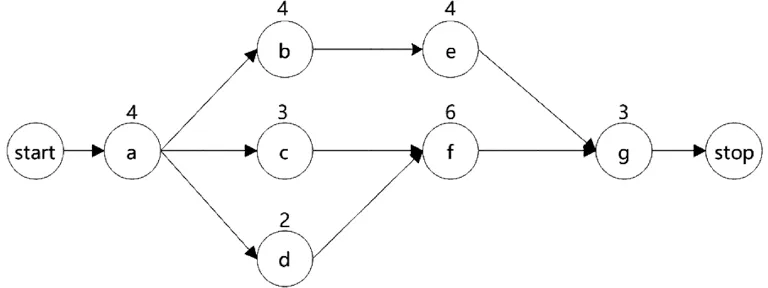
图1 项目1 单代号网络图

图2 项目2 单代号网络图

由图1 和图2 可知，2 个项目均共有9 个活动，其中包括2 个不占用时间也不消耗资源的虚节点（开始节点和结束节点）。项目完成共需3 种可更新资源，包括高级人力资源、专用设备资源及普通人力资源。每个活动对每种资源每日的需求量为固定值，3 种资源的权重系数ω分别为0.4、0.4、0.2。每个活动的日均资源消耗量、最早开始时间、最晚开始时间、浮动时间及紧前活动的相关参数见表1。

表1 项目活动参数表

由表1 可知：项目1 的开始时间为0，完工时间为16；项目2 的开始时间为0，完工时间为15。通过在2 个单代号网络图的首尾各自添加一个辅助活动将两个单代号网络图合并为1 个大的单代号网络图并对各活动重新编号，结果见图3。项目1 的辅助活动分别为1-1 和1-2，项目2 的辅助活动分别为2-1 和2-2。合并后的项目开始时间为0，完工时间为16。辅助活动1-1、1-2、2-1、2-2 的持续时间分别为0、0、0、1，且辅助活动不占用任何资源。

图3 多个网络图转换为一个网络图

3.2 使用MATLAB 遗传算法工具箱进行求解

表1 中关键路径上的活动浮动时间为0，其他为非关键链上的活动。该算例的关键路径共2 条，分 别 为1-1 →a1 →c1 →f1 →g1 →1-2 和2-1 →a2 →b2 →e2 →g2 →2-2。通过调整非关键链上活动的开始时间，可实现在工期固定条件下的资源平衡。由于MATLAB 遗传算法工具箱本身是以函数最小值作为优化目标，而本算例也需要求解目标函数的最小值，因此直接使用目标函数作为适应度函数，便可将资源平衡问题转化为遗传算法的最优问题进行求解。

根据前文确定的资源优化数学模型，目标函数为：

从以上数学模型可以看出，参数由6 个不等式约束且每个参数有对应的取值范围。这6 个不等式体现了活动紧前关系的约束。对6 个参数及其取值范围做如下处理，转换为12 个线性约束条件：

计算过程如下。

第一步，使用MATLAB 遗传算法工具箱对适应度函数进行编程，编程后将其导入遗传算法工具箱的相应位置。主要编程思路为：（1）根据天数（16）和活动数（14），建立日期-活动矩阵（0-1 矩阵）；（2）将关键链上的活动放入对应行列中（固定位置，对应位置元素置1）；（3）将非关键链活动放入对应行列中（根据最早活动开始时间X1～X6，根据开始时间的判断结果将相应位置元素置1）；（4）根据各活动的日均3 种资源占用情况，分别生成日期-资源矩阵；（5）根据日期-资源矩阵和各类资源的权重，计算3 种资源的资源波动方差之和。

第二步，将X1～X6 的12 个限制条件作为线性约束条件，输入到遗传算法工具箱中相应位置。

第三步，输入遗传算法工具箱中的其他参数（初始种群大小、进化代数以及选择、变异、交叉方法等，此处均使用默认值）。

第四步，对算例进行计算。运行结果如图4 所示，在迭代50 次后得到的最佳适应度为4.4375，此时资源需求波动的方差为4.4375。最优染色体对应的X1=5，X2=4，X3=9，X4=4，X5=4，X6=8，即对应优化后各个活动的开始时间为：AS（b1）=5，AS（d1）=4，AS（e1）=9，AS（c2）=4，AS（d2）=4，AS（f2）=8。

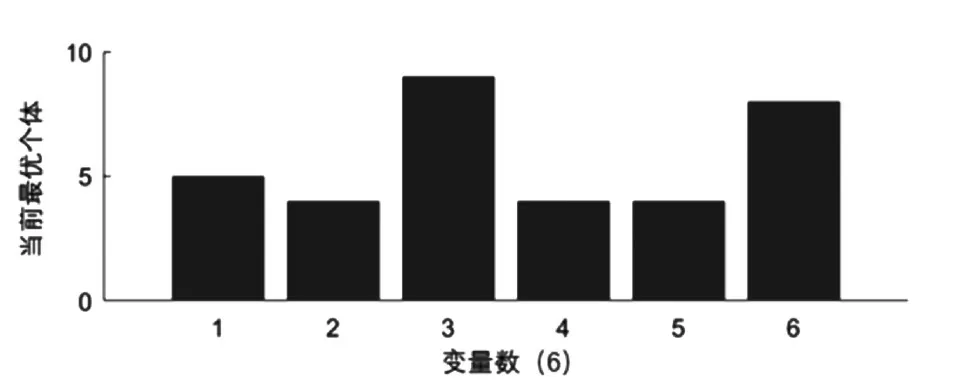
图4 染色体进化结果

由于受突发事件影响，该企业的维保工程项目可能无法严格按照计划开展，因此不可仅通过对资源计划的比较验证资源平衡的优化效果，需要统计资源负荷情况比较优化效果。同时，如果比较时间较短，受月工作量波动影响较大，因此需要统计一定时期内的资源波动情况来减少工作量波动对评估结果的影响。本研究通过在该企业S 省区维保项目推进中应用该资源平衡方案，并统计该方案应用前3个月（6月、7月、8月）和应用后3个月（9月、10月、11 月）关键人力资源A、关键设备资源B、普通人力资源C 的需求情况，得到优化前及优化期间的负荷图见图5 和图6。由于不同资源权重不同且优化目标为降低整体资源负荷的波动，因此单纯从优化前和优化期间的资源负荷图不易看出资源的波动是否得到抑制。本研究进一步使用资源平衡目标函数对3 种资源（权重ω分别设置0.4、0.4、0.2）的综合使用平衡情况进行方差计算，以验证资源优化效果。计算结果显示，优化前的资源负荷波动方差为5.785，优化期间的资源负荷波动方差为3.185，表明该方案对该企业开展资源平衡工作起到了一定的帮助。

图5 S 省3 种资源使用优化方法前负荷图

图6 S 省3 种资源在使用优化方法期间负荷图

4 小结

本研究通过对某医疗器械生产企业维保工程多项目管理中存在的问题进行分析，提出了优化1 个月内进度安排，以便能够有足够的剩余资源应对紧急维修等突发情况的目标。将各项目网络图合并为一个网络图的同时对优化过程和优化目标进行建模，使用MATLAB 遗传算法工具箱对适应度函数编程并对模型进行求解，根据求解结果调整非关键链上活动的开始时间，进而实现了资源平衡优化。使用算例对具体计算过程进行了展示，同时通过在实际工作中运用该优化方案进行项目进度安排，对比优化前与优化期间资源负荷方差的方式对优化效果进行检验，验证了该方案对于资源平衡的优化具有一定的效果。