基于PVMD和MMDE的滚动轴承故障诊断
2023-07-12梁彬彬叶井启刘振鹏
安 冬,梁彬彬,叶井启,邵 萌,刘振鹏
(1.沈阳建筑大学机械工程学院,辽宁 沈阳 110168;2.辽宁江扬科技有限公司,辽宁 沈阳 110000)
旋转机械作为工业生产中的主要设备,其运行健康状况与工业生产效率直接相关。而滚动轴承作为旋转机械中不可缺少的重要机械零部件发挥着重要作用,多项研究表明,旋转机械中的大多数机械故障是由滚动轴承所引起[1]。由于来自轴承的振动信号是非线性的,具有非平稳特性,并且在信号的采集过程中极易受到硬件设备和环境的影响[2]。因此,如何在复杂的信号中提取有效的故障特征是完成故障判别急需解决的问题[3]。
经验模态分解[4](Empirical Mode Decomposition,EMD)是一种常见的分解方法被应用于各个领域。EMD主要优点是可以在没有经验的情况下通过数据驱动进行信号处理[5]。经验模态分解具有完备性和自适应性等特点,在滚动轴承的信号降噪和故障特征提取中引起了研究人员的广泛关注[6]。但是,EMD方法本身具有一些缺点,导致信号分解的结果容易出现端点发散现象,以及一些其他不可避免的缺点[7]。针对这些问题,K .Dragomiretskiy[8]等提出一种变分模态分解(Variational Mode Decomposition,VMD)的自适应信号处理方法,与EMD方法不同,VMD引入了一种完全非递归的方式将信号分解问题转化为约束优化问题,采用迭代更新的方式求解约束变分模型,可以自适应的将振动信号分解为一定数量且有限带宽的固有模态分量[9]。这样既能避免EMD方法在分解时存在的过包络、欠包络问题,又保留了EMD的优点。近些年来,有许多学者对此进行研究:郑近德等[10]将故障信号经VMD分解重构后,计算初始特征的复合多尺度模糊熵完成特征提取。马增强等[11]采用VMD结合独立分量分析对故障信号进行去噪处理,从而实现了故障类型的判断。
熵作为一种度量不确定性或不规则性的方法,其采用系统状态的概率分布来量化时间序列的规律性,表示时间序列的复杂程度[12]。许多能够反映振动信号非线性特征分析方法如:样本熵[13]和排列熵[14]等,已被大量学者研究应用于不同领域。然而在实际应用中发现,上述方法忽略了振幅的平均值和幅度值间的不同,并且计算比较复杂,还可能会造成幅度信息的某些丢失[15]。国外学者M.Rostaghi等[16]以散布熵(Dispersion Entropy,DE)为指标,作为新的方法来衡量时间序列的不规则程度,量化序列的规律性,具有运算速度快、不易受突变信号影响且考虑了幅值间关系等优点,在一定程度上解决了样本熵和排列熵的缺陷[17]。由于滚动轴承振动信号中含有复杂的特征信息,单一尺度下的熵值往往不能得到深层次的故障信息,为了分析不同时间尺度上时间序列的复杂性需要对故障信号进行均值多尺度分析。
由于轴承原始振动信号表现出的复杂特征,笔者提出了一种基于主成分变分模态分解法(Principal Variational Modal Decomposition,PVMD)和均值多尺度散布熵(Mean Multiscale Dispersion Entropy,MMDE)的滚动轴承故障诊断方法。先采用PVMD对轴承原始信号进行预处理[18];再对初始特征信号进行MMDE的运算,可以有效地提取轴承故障特征向量,从而全面表征轴承故障信号的细节信息;最后采用支持向量机对故障状态进行判别。研究表明,笔者所提方法实现了滚动轴承故障类别的准确诊断。
1 基于PVMD和MMDE的故障特征提取
1.1 主成分变分模态分解
主成分变分模态分解法(PVMD)是采用VMD将原始故障信号分解,VMD利用迭代更新的方式求解约束变分模型的最优解,可以自适应的将振动信号分解为一定数量且有限带宽的固有模态分量,从而实现自适应分解。再结合主成分分析按95%累计贡献率去除IMF的冗余信息降低特征信号维度,简化为能够表征原始振动信号的少数几个主元成分,从而反映出故障特征信息,有效降低了数据的分析难度和复杂程度。
构建受约束变分模型:
(1)
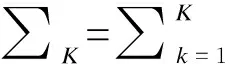
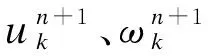
(2)
(3)
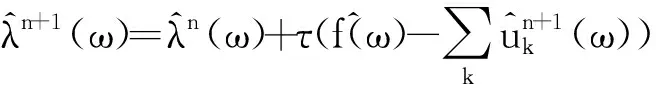
(4)
重复上述步骤,使每个模态分量的频率及频带在迭代求解过程中持续更替,达到更替的终止条件便可结束:
(5)
对VMD分解的一系列本征模态函数进行中心化处理,得到特征参数矩阵X。
计算矩阵X的平均值与协方差矩阵,并求取协方差矩阵的特征值和特征向量。将特征值按从大到小进行排序,同时将特征向量按特征值从大到小的顺序依次排列构成矩阵P。
计算特征矩阵,按照累计贡献率θ选取前k个特征,得到主元模态函数(PIMF)。
(6)
1.2 均值多尺度散布熵
基于上节采用PVMD对轴承信号进行预处理得到的PIMF分别进行MDE运算,求取其平均值形成均值多尺度散布熵(MMDE)来完整量化振动信号在多个时间尺度上的故障特征。在计算多尺度序列的DE值时整个计算过程中平均值μ与标准差σ是基于原始数据的μ和σ且保持不变。计算步骤如下:
(1)构建新序列
对于长度为L的时间序列u={u1,u2,…,uL},u被划分成尺度因子为τ的新序列。然后构造粗粒化信号:
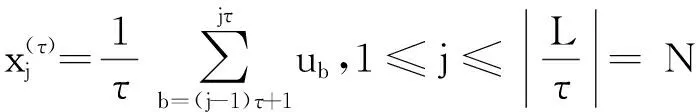
(7)
(2)计算每个粗粒化信号的熵值
使用标准正态累积分布函数:
(8)
将时间序列x从0到1映射到y={yj,j=1,2,…,N},yi∈(0,1)。其中μ和σ2分别表示期望和方差。
将y映射到[1,2,…,c]内,其中c为类别个数。
(9)
(3)计算嵌入向量
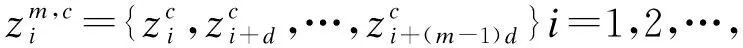
N-(m-1)d.
(10)
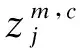
(4)计算散布模式πv0v1…vm-1相对频率
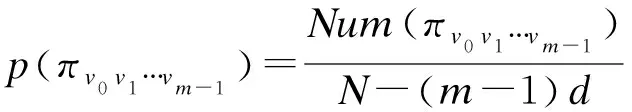
(11)
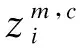
(5)根据信息熵理论定义散布熵
ln(p(πv0v1…vm-1)).
(12)
(6)各个尺度因子τ下的MDE定义
(13)
(7)MMDE定义
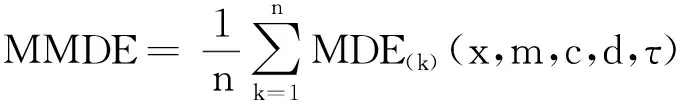
(14)
式中:n为故障样本进行MDE运算的特征数据个数。
2 基于PVMD和MMDE的故障诊断方法
2.1 故障诊断流程
基于PVMD和MMDE的故障轴承判别步骤如下:
Step1.采用传感器按照特定频率收集轴承不同状态下的故障信号,获取各种状态下的样本数据;
Step2.采用主成分变分模态分解算法对原始振动信号进行去噪预处理,对分解的一系列本征模态分量分析降维,得到初始特征数据;
Step3.计算初始特征数据的均值多尺度散布熵构建故障特征向量;
Step4.采用SVM用作模式分类方法。将特征向量输入训练好的SVM中,从而完成轴承故障的判别。
2.2 实验数据分析
实验数据来自西储大学轴承数据中心的滚动轴承振动信号。采用笔者所提出的PVMD和MMDE的判别方法来进行实验分析,以此来验证所提方法的有效性。以驱动端收集的故障振动信号作为目标对象,并以频率为12 kHz进行采样,负载设置为1.492 kW,电机转速约为1 750 r/min。实验数据集的轴承振动信号包含内圈故障、外圈故障、滚动体故障和正常状态,其中单点故障直径为0.533 4 mm。每种轴承故障类型的振动信号样本取40组,每组样本信号含有1 024个点,共需采集160组样本数据。滚动轴承内圈故障中一组样本信号波形图如图1所示。
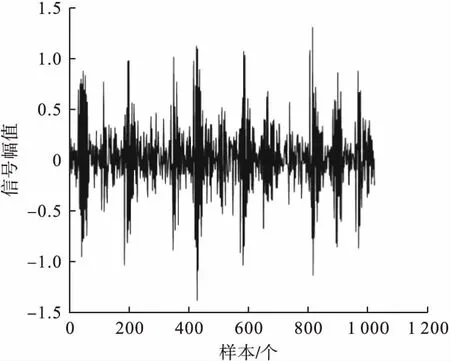
图1 内圈故障信号时域波形Fig.1 The fault signal of the inner ring in time domain
2.3 轴承故障特征提取
故障信号由变分模态分解法分解成一定数量的固有模态函数,为了防止出现欠分解和过分解现象,采用观察法来进行模态个数K值的确定。K值不同会对分解的结果产生重要影响,从而影响最终的识别效果。如果分解个数过多会出现频率混叠,则认为出现了过分解现象;如果分解个数过少,故障信号的某些重要特征可能丢失难以实现信号的有效分解,则认为出现了欠分解现象。不同分解个数时的中心频率如表1所示。
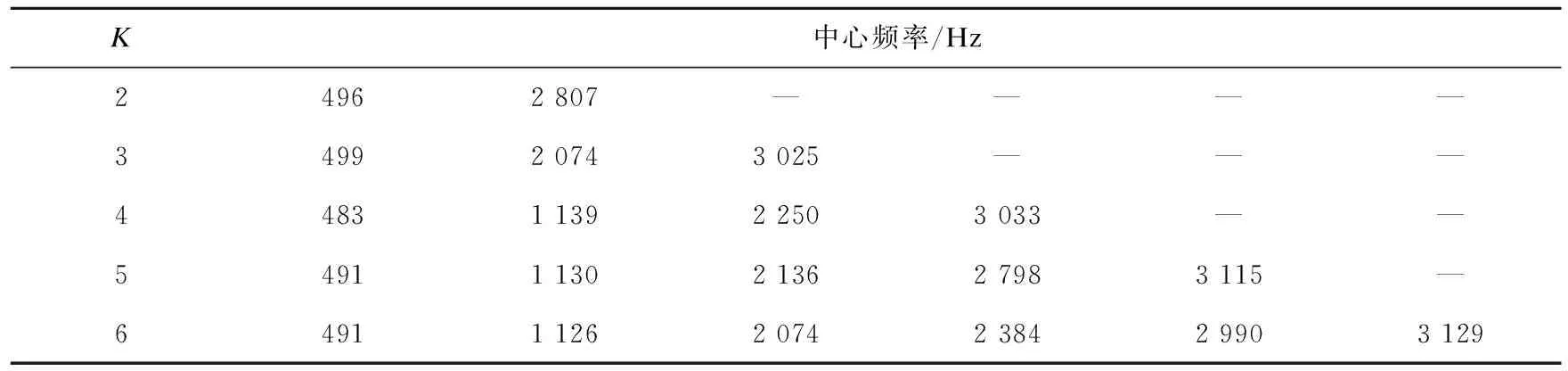
表1 不同分解个数的中心频率Table 1 The center frequencies of different decompositions numbers
由表1可知,当K=4时各分量的频率相距较远,分解个数明显不足出现了欠分解现象。当K=6时分量的频率又相距较近出现了混叠,即可认为出现了过分解。因而分析出模态数K=5。经VMD分解后的内圈故障时域图如图2所示。
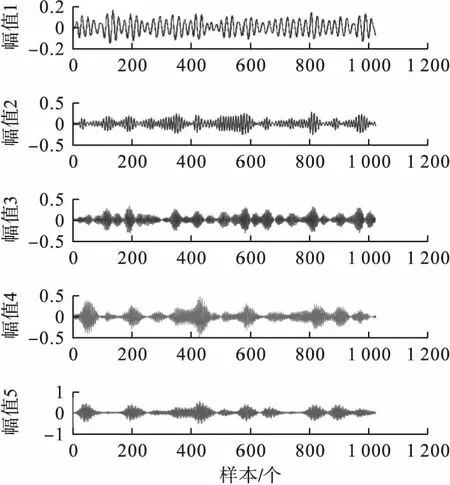
图2 内圈故障信号VMD分解结果Fig.2 The VMD decomposition result of fault signal for inner ring
随后采用主成分分析法对经过VMD分解的一系列本征模态分量进行降维去噪处理,提取主元成分。主元个数的选取原则主要依据累计贡献率θ,提取θ高于95%的主要成分(见图3)。由图3可知,前4个主元分量的累计贡献率已达到了95%,根据贡献率选取原则选择前4个初始特征进行均值多尺度散布熵运算,降维后的主元分量时域图如图4所示。
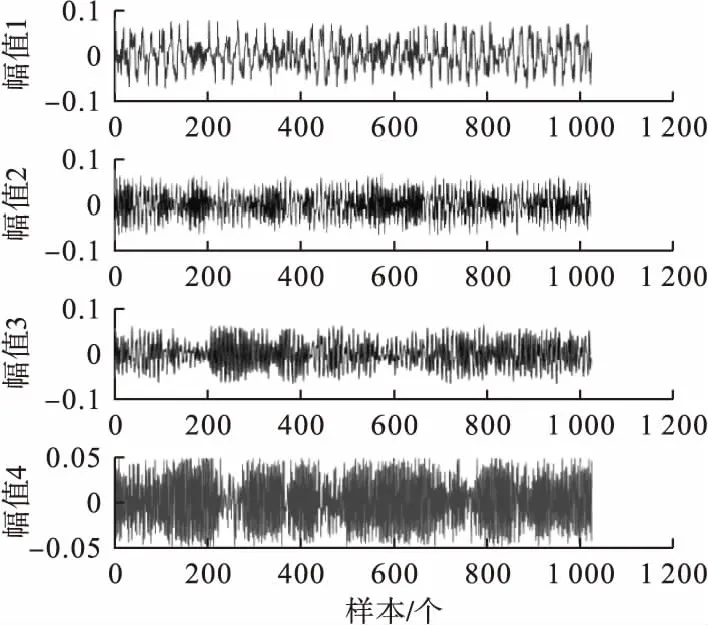
图4 降维后各主元时域图Fig.4 The principal components after dimensionality reduction in the time domain
根据上文定义的均值多尺度散布熵求取各个初始特征的熵值。在计算过程中需要事先确定有关计算参数,嵌入维数的取值不宜过大或过小,越大就有越多的详细信息,但需要的数据长度也会随之增加;过小则可能检测不到信号中的动态变化,通常取2或3。对于类别通常在[4,8]选取其中的一个整数。对于时延在有关散布熵的算法中一般取1。详细过程可文献[11]。经过计算可以得到轴承不同状态的MMDE熵值曲线(见图5)。
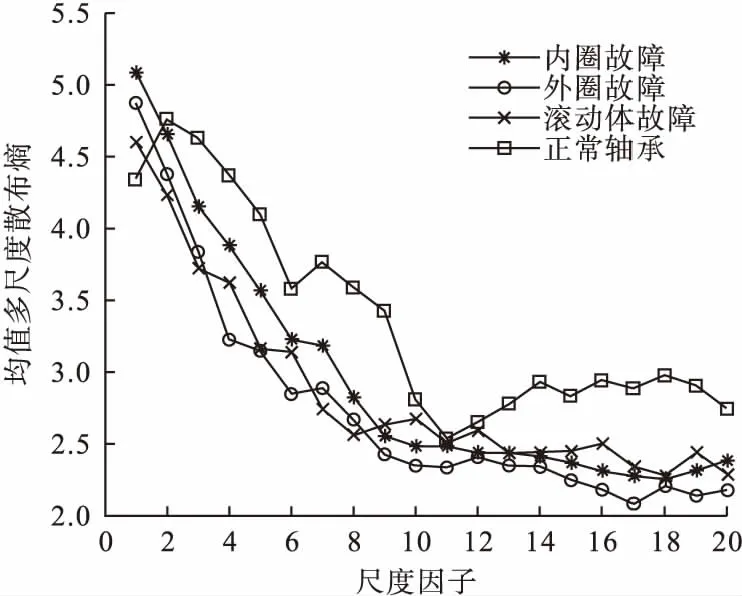
图5 四种轴承状态的熵值图Fig.5 Entropy map of four bearing states
由图5可知,熵值随着尺度的不断增加而逐渐减小;当尺度大于8时,均值多尺度散布熵值而逐渐趋于平缓,为了更好的识别滚动轴承故障故选取每个样本数据前8个尺度的熵值作为特征向量,输入到SVM中进行故障诊断。表2为滚动轴承四种故障数据经PVMD和MMDE运算处理后得到的滚动轴承熵值特征向量,其中每种故障状态只列出2组样本数据。
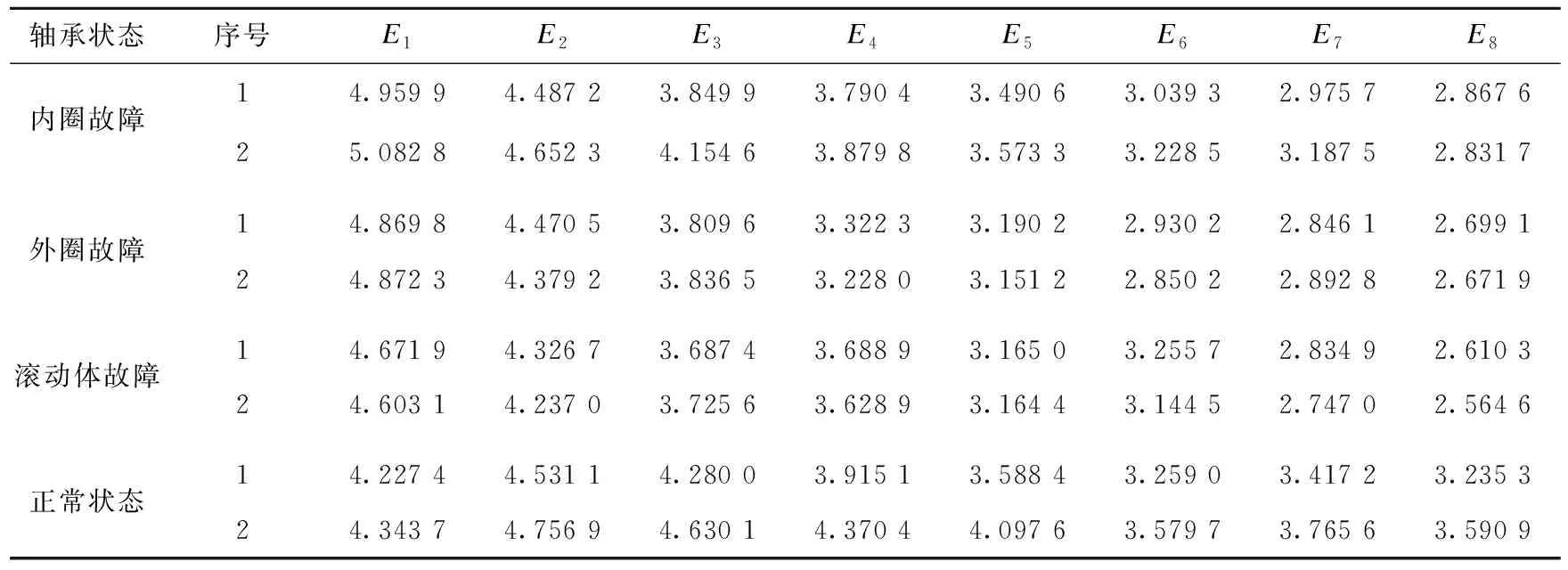
表2 滚动轴承熵值特征向量Table 2 Characteristic vector of entropy value for rolling bearing
2.4 实验结果分析
SVM广泛应用在数据样本较少的轴承故障诊断中,故基于文中的实际情况选择此种故障识别方法。已知每种故障类型的振动信号各40组,共计160组样本数据,基于上述特征提取方法从每种振动信号中随机选取10组特征向量作为训练样本,用训练好的SVM分类器将剩余的30组特征向量进行测试。其中,纵坐标的样本类别标识1~4分别代表内圈故障、外圈故障、滚动体故障和正常状态。测试样本的识别结果如图6所示。由图6可知,外圈、滚动体和正常状态均达到了准确识别,仅有2组判别出错,将内圈错诊为滚动体故障。笔者对识别结果做了总体统计,如表3所示。由表3可知,平均故障识别准确率达到98.33%。
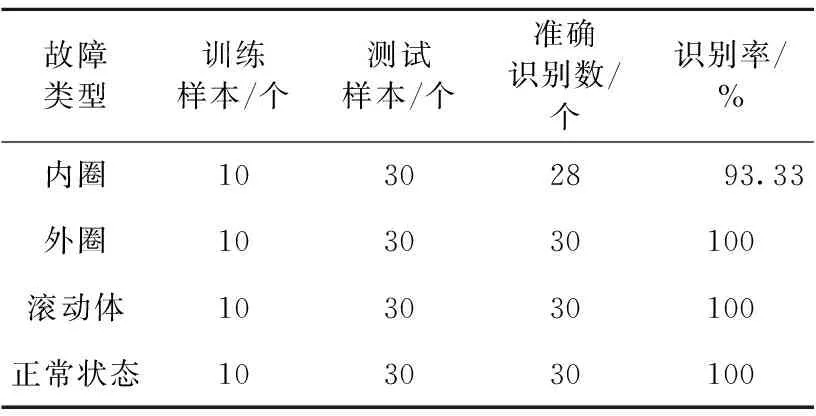
表3 PVMD-MMDE识别结果Table 3 The identification results of PVMD-MMDE
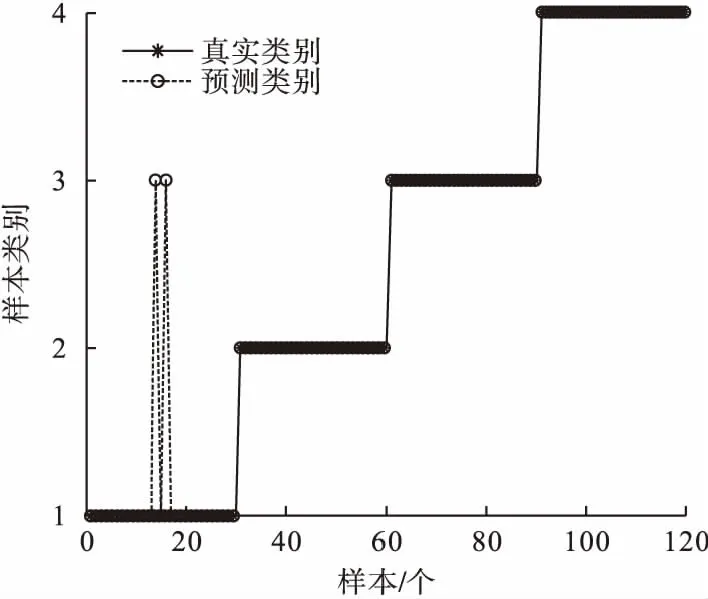
图6 PVMD-MMDE样本识别结果Fig.6 The identification results of PVMD-MMDE
为了进一验证笔者所提方法的优越性选用同样的样本数据设置了3组对比实验,第一组直接对VMD分解出来的本征模态函数进行MDE运算,第二组对VMD分解出来的本征模态函数进行MMDE运算,第三组对PVMD分解出来的初始特征数据进行MDE运算,然后分别借助SVM分类器进行识别分类。四种故障类型的诊断结果如图7、图8和图9所示,平均识别率分别为89.17%、90.83%和94.17%,总体统计结果见表4。通过对比两表可以得知笔者方法的故障识别率高于对比实验,说明了提出的轴承故障判别方法具有更佳的识别效果。

表4 对比实验的故障状态识别结果Table 4 The fault state identification results of the comparative experiment %
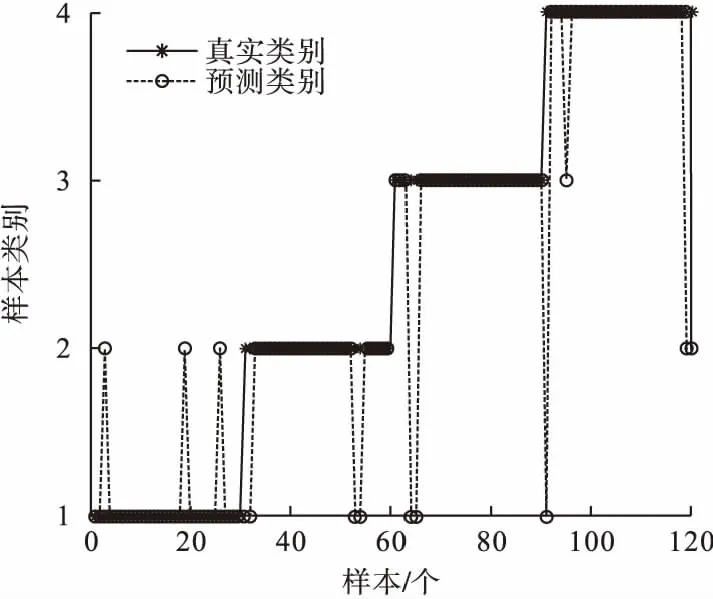
图7 VMD-MDE样本识别结果Fig.7 The identification results of VMD-MDE
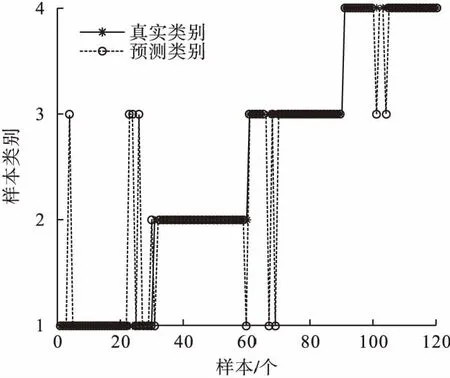
图8 VMD-MMDE样本识别结果Fig.8 The identification results of VMD-MMDE
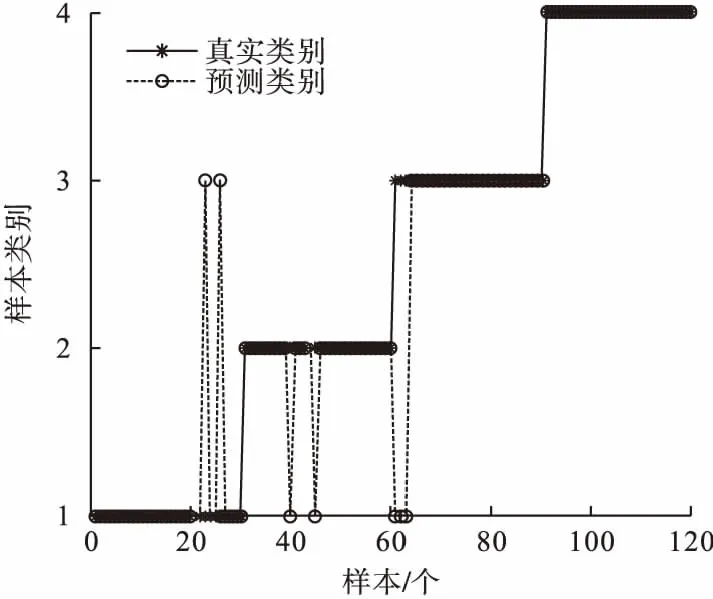
图9 PVMD-MDE样本识别结果Fig.9 The identification results of PVMD-MDE
3 结 论
(1)在变分模态分解的基础上结合主成分分析对轴承原始故障数据进行降噪分析预处理,从而得到降维的主元模态分量,有效降低了数据的分析难度和复杂程度;采用均值多尺度散布熵的方法来全面表征特征向量的细节信息,可避免局部信息的丢失,可以有效提取轴承故障特征向量。
(2)采用具有良好分类效果的支持向量机对故障状态进行识别,可以准确判别出轴承故障。
(3)PVDM-MMDE的故障识别率为98.33%,对比实验的识别率分别为89.17%、90.83%和94.17%,验证了笔者所提方法对故障诊断具有很好的识别效果,进一步提高了轴承故障诊断的识别率。
