油基石墨烯纳米流体黏度变化规律研究
2023-07-12张丽秀魏晓奕王俊海赵文哲
张丽秀,张 营,魏晓奕,王俊海,赵文哲
(1.沈阳建筑大学分析与检测技术研究中心,辽宁 沈阳 110168;2.沈阳建筑大学机械工程学院,辽宁 沈阳 110168;3.沈阳建筑大学材料科学与工程学院,辽宁 沈阳 110168)
由于电主轴具有高转速且连续加工等特点,服役过程中在轴承腔内部产生大量热沉积,造成热变形及主轴精度降低等情况。因此需要有效的润滑方式或改善润滑油减低轴承温升。电主轴通常采用油气润滑,利用压缩空气提高换热率,并利用液体润滑油改善摩擦环境,但在高速转动情况下,还是存在欠润滑及换热率不足的现象。在润滑油中加入固体相形成混合润滑方式,在欠润滑时利用固体润滑代替液体润滑并提高导热率,是解决轴承温升的有效途径。
纳米流体的出现及快速发展为轴承散热问题提供了新的解决方案[1-3]。纳米流体是将纳米级的固体颗粒添加进水、乙二醇或油等基础液中,以达到提高基础流体导热系数的目的。已有研究表明,添加一定体积分数的纳米颗粒对基础流体导热性能的提高效果是显著的[4]。同时纳米颗粒的加入也会影响流体的黏度,黏度和导热系数是纳米流体应用的两个重要热物理性能指标。黏度解释了流体层间内阻,将纳米颗粒分散在流体中,如果流体受到剪切,则在流体层之间存在阻力增加的可能性,导致纳米流体黏度的增加[5]。润滑油黏度变化直接影响润滑抗压能力,也会影响纳米流体热物理性质。
M.Kole等[6]研究了颗粒聚集对CuO-齿轮油纳米流体黏度的影响,结果表明,随着纳米颗粒体积分数的增加,流体的黏度升高,齿轮油的牛顿行为向非牛顿行为转变;随着温度升高,流体黏度降低。此外,M.Kole等[7]还研究了石墨烯纳米流体的热导率、黏度和电导率的变化,结果表明,纳米流体的热导率和黏度都是石墨烯体积分数和温度的函数,制备的纳米流体和基液(EG+DW)黏度均表现出非牛顿特性,其中体积分数0.395%的纳米流体与基液相比,表现出剪切变稀。W.Y.Lai等[8]研究了基液为去离子水和丙二醇的Al2O3纳米流体的黏度变化,结果表明,添加纳米颗粒后流体的相对黏度增加,并且在加热管中流动纳米流体表现更高的相对黏度。M.Mehrali等[9]研究了水基石墨烯纳米流体的导热性和流变特性,在基液中添加了具有不同比表面积的纳米片,结果表明,水基石墨烯纳米流体的流变特性接近牛顿和非牛顿行为,黏度随温度的升高而线性降低。在低浓度下,基液对流体剪切变薄起主要作用。J.P.Vallejo等[10]将功能化的石墨烯纳米颗粒分散在质量比为30∶70的丙二醇和水的混合物中,并对其施加恒定剪切速率,结果发现流体黏度变化与剪切速率和测试时间无关,石墨烯纳米流体表现出牛顿行为。M.R.Esfahani等[11]研究了粒径和黏度对水基氧化石墨烯纳米流体导热系数提高的影响,结果表明,存在一个氧化石墨烯最佳浓度,在该浓度下,粒径和黏度显著提高,而纳米流体黏度的进一步提高对导热系数的提高无明显影响。X.C.Hu等[12]研究了温度、颗粒质量分数和剪切速率等因素对石墨/机油(5W-40)纳米流体黏度的影响,结果表明,温度是影响纳米流体黏度的最主要因素。此外,不同体积分数的纳米流体在低剪切速率下表现为牛顿流体,在较高的剪切速率下观察到剪切变稀,表现为明显的非牛顿流体。纳米流体黏度随温度、剪切速率及纳米粒子质量分数等因素呈非线性变化。这种纳米流体黏度的提高可以通过固—液均质方程来估计,使用这些理论模型预测流体黏度的前提是必须满足线性流体假设[13-15]。事实上,目前关于黏度变化预测模型几乎不能预测纳米流体在更高颗粒体积分数范围内的黏度,并且均未考虑流体黏度的温度依赖性以及添加纳米颗粒性质的影响。如果在轴承运行工况下润滑油黏度偏离标称性能,会导致油品承载能力、传热特性等发生改变,严重时可直接威胁轴承安全稳定运行[16]。因此,准确掌握润滑油的黏度变化对于科学计算轴承温升具有重要意义。
现有研究主要集中于水基金属及其氧化物形成的纳米流体,关于油基碳族固体颗粒纳米流体黏度的变化规律研究较少。基于此,笔者采用“两步法”制备了石墨烯润滑油纳米流体,通过XRD和静置观察法对石墨烯结构及石墨烯润滑油分散稳定性进行表征;同时还考虑了超声时间、颗粒质量分数及温度对纳米流体黏度的影响,并基于最小二乘法提出了一个石墨烯润滑油纳米流体黏度随超声时间、质量分数和温度变化的数学模型。研究表明:超声作用主要通过减小石墨烯粒径尺寸来降低石墨烯润滑油黏度;石墨烯在润滑油中的添加质量对其黏度的影响呈非线性;温度升高,所有石墨烯润滑油的黏度出现降低。
1 石墨烯纳米流体的制备与表征
1.1 石墨烯纳米流体的制备
使用青岛德通纳米技术有限公司生产的SG-01005型号石墨烯,通过X射线衍射技术(XRD)表征石墨烯的纳米结构。图1为石墨烯的XRD图像。

图1 石墨烯的XRD图像Fig.1 The XRD image of graphene
从图1中可以看出,该石墨烯纳米颗粒(002)晶面衍射峰相对于石墨出现右移,且峰面变宽,强度减弱,证明石墨烯纳米层间距离变大,单片尺寸减小,晶体结构完整性下降,无序度增加。在40~50°间出现的(100)、(101)衍射峰表明了石墨烯的取向性较弱。润滑油选用美孚DTE轻级-32号涡轮循环系统油。首先,将称重的石墨烯纳米粉末加入润滑油中,为防止其发生团聚和沉淀,通过磁力搅拌将二者混合,采用超声波细胞破碎仪(型号ZOLLO-1000Y)对悬浮液中纳米颗粒进行分散。图2为石墨烯润滑油纳米流体制备流程。最终制备得到不同质量分数(0,0.05%,0.1%,0.5%,1.0%)的石墨烯润滑油。
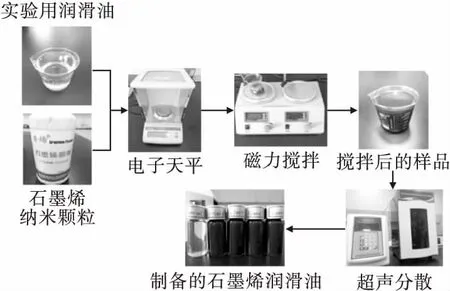
图2 石墨烯润滑油纳米流体制备流程Fig.2 The preparation process of graphene lubricant nanofluid
1.2 石墨烯纳米流体的分散稳定性表征
纳米粒子由于自身以及与周围液体分子之间的范德华相互作用,在基液中容易形成团聚,进而影响纳米流体稳定性和热物理性质。为了确定添加石墨烯纳米颗粒后纳米流体的稳定性,笔者采用了静置观察法对其进行表征。石墨烯润滑油纳米流体的静置观察在室温,无阳光直射的环境下进行。观察油样均经过超声功率600 W,时长45 min的分散处理。图3为不同静置时间的石墨烯润滑油纳米流体观察结果。图3(a)为刚经过超声分散后的石墨烯润滑油纳米流体,可以看出石墨烯颗粒均匀分布在润滑油中,所有样品均未出现明显的分层现象;图3(b)为静置2 d后的石墨烯润滑油,除质量分数为0.5%的样品外,其余样品出现不同程度的沉淀,表明石墨烯开始聚集并形成不同尺寸的团聚体。其中,质量分数为1.0%的石墨烯润滑油沉淀现象最为严重,可以看出已经与润滑油形成明显的固液分层。图3(c)为静置5 d后的样品,质量分数为0.5%的石墨烯润滑油仍保持较好的稳定性,只在样品溶液的上表面出现轻微的固液分层;而在其余样品中,较大尺寸的团聚体全部沉淀,未聚集或尺寸较小的纳米颗粒仍保持悬浮状态。图3(d)为石墨烯润滑油静置20 d的观察结果。可以看出:质量分数为0.5%的样品出现轻微“挂壁”现象外,其余样品已全部沉淀,并且质量分数为0.5%的石墨烯润滑油也出现了明显的沉淀现象。从静置观察的总体结果来看,质量分数为0.5%的石墨烯润滑油纳米流体稳定性相对较好,而质量分数为1.0%的样品分散稳定性在测量的范围内表现最差。

图3 不同静置时间的石墨烯润滑油纳米流体观察结果Fig.3 The comparation results of graphene lubricant nanofluid with different standing time
1.3 石墨烯纳米流体的流变性表征
轴承用石墨烯润滑油除了要有良好的分散稳定性外,还需具有良好的流变性能。了解石墨烯润滑油的流变行为,有助于确定纳米流体黏度随剪切速率变化的曲线。若剪切应力对剪切速率的变化呈线性规律,那么石墨烯润滑油表现为牛顿行为,该润滑油即为牛顿流体。图4为石墨烯润滑油剪切应力Z随剪切速率γ的变化规律。
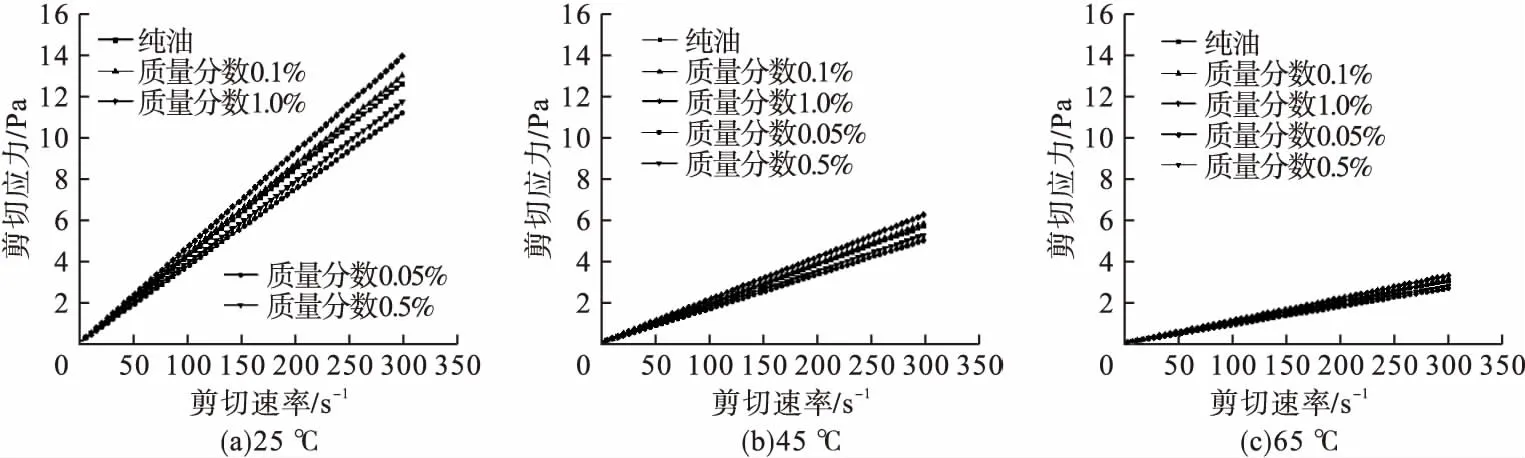
图4 石墨烯润滑油剪切应力随剪切速率的变化规律Fig.4 The shear stress variation of graphene lubricating oil with shear rate
由图4可知,在25 ℃、45 ℃及65 ℃的条件下,随着剪切速率的增加,纳米流体内部的剪切应力呈线性增加,表明了石墨烯润滑油纳米流体在测量范围内具有牛顿行为。
2 石墨烯纳米流体黏度影响因素实验
将石墨烯均匀分散在润滑油中形成石墨烯润滑油纳米流体,其黏度变化主要受温度、石墨烯质量分数、粒径的影响。笔者通过实验研究了石墨烯润滑油纳米流体黏度随超声时间,颗粒质量分数及温度等影响因素的变化规律。
2.1 实验方法及条件
为了获得石墨烯润滑油在不同工况下的黏度变化趋势,选取了方瑞仪器生产的NDJ-8S数字式黏度计,该黏度计广泛应用于油脂、浆料等实验样品,满量程测量精度不大于±2.0%。在实验开始前,通过硅油黏度标准液(5 200 cp)对仪器进行校准,确定了黏度计具有较高的精度和重现性。
通过调节超声细胞破碎仪工作时间,可以确定超声作用对石墨烯润滑油黏度的影响。由于超声作用使石墨烯及油分子的能量升高,导致实验样品的温度发生变化。为了获得更加准确的实验结果,通过加装恒温浴槽对石墨烯润滑油进行控温。对不同工况下的石墨烯润滑油黏度值分别测量三次,取其平均值。根据以上理论依据设计实验方案,实验参数如表1所示。

表1 石墨烯润滑油黏度实验参数Table 1 The experimental parameters of viscosity for graphene lubricating oil
2.2 实验结果及分析
2.2.1 超声时间对石墨烯润滑油黏度的影响
通过超声波处理提高纳米流体的分散稳定性已被证明是有效的,如果未进行超声分散的石墨烯润滑油进入摩擦副中,将降低润滑效果[17]。合适的超声分散可以获得更小的纳米粒子,也必将影响润滑油的黏度。笔者对不同质量分数的石墨烯润滑油纳米流体进行超声分散,通过NanoPlus-3纳米粒度与Zeta电位分析仪和旋转黏度计来获得超声时间对石墨烯粒径均值及纳米流体黏度的影响。
(1)对石墨烯粒径均值的影响
对石墨烯润滑油进行超声处理,可以有效地减少石墨烯在润滑油中形成的团聚体的尺寸和数量。图5为常温条件下质量分数0.5%的纳米流体石墨烯平均粒径和黏度随超声时间变化规律。
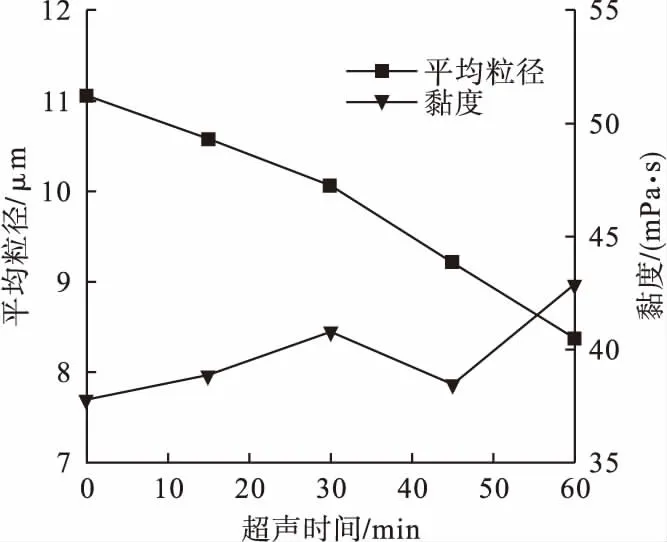
图5 纳米流体石墨烯平均粒径和黏度随超声时间变化规律Fig.5 The variation of particle size,average size and viscosity of graphene with ultrasonic time
由图5可知,在超声处理的前30 min时间内,团聚体的尺寸几乎呈线性增加,但黏度出现降低趋势,这是由于超声作用使部分粒径较小的石墨烯处于“高能活跃”状态,更易吸附于附近较大片径的石墨烯上,导致团聚体的尺寸增加,同时石墨烯在润滑油中的单体数量下降,降低了纳米流体层与层之间的无序度,导致黏度出现降低;在45 min时,纳米流体中的团聚体尺寸达到最低。与此同时,粒径较小的团聚体在基液中占比开始增加,表明此时获得石墨烯团聚体的最佳尺寸,黏度进一步降低;当超声时间继续增加,团聚体尺寸再一次增大。由于分子间范德华相互力增加,纳米流体剪切层数量减少,导致黏度仍保持降低趋势,此时为了减少团聚体尺寸应选择更高的超声功率进行分散。上述情况表明,超声分散有助于纳米流体获得尺寸较小的团聚体和较低的黏度,但对不同质量分数纳米流体,应选择合适的超声时间和超声功率。
(2)对石墨烯纳米流体黏度的影响
超声波分散为纳米流体常用的分散方法之一,因此笔者采用超声方法对石墨烯润滑油进行初步分散。由于超声作用会影响石墨烯纳米颗粒在润滑油中的聚集行为,降低石墨烯团聚体的尺寸,进一步降低石墨烯润滑油的黏度。图6为不同温度下石墨烯润滑油黏度随超声时间的变化规律。
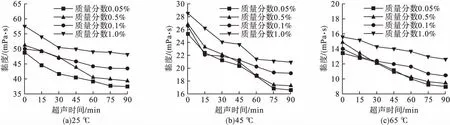
图6 不同温度下石墨烯润滑油黏度随超声时间的变化规律Fig.6 The viscosity variation of graphene lubricating oil with ultrasonic time at different temperatures
由图6可知,随着超声时间的增加,石墨烯润滑油的黏度降低。当超声时间达到一定范围时,纳米流体的黏度值几乎保持稳定。对于石墨烯质量分数较低的样品,黏度达到最小值所需要的超声时间较短;对于高质量分数的石墨烯润滑油,黏度达到最低值需要更多的超声时间。以质量分数0.1%和1.0%石墨烯润滑油为例,在室温条件下,质量分数0.1%的石墨烯润滑油黏度值达到稳定需要60 min超声时间,而质量分数1.0%的石墨烯润滑油至少需要75 min。
这是由于较低质量分数的石墨烯润滑油中形成的颗粒团聚体尺寸较小,分子间的范德华相互作用较弱,超声波作用以高能高震降低了石墨烯的表面能,将聚集的石墨烯拆散开来,从而降低了石墨烯润滑油的黏度。而在较高质量分数的石墨烯润滑油中,形成的颗粒团聚体尺寸较大,分子间的范德华相互作用较强,实验所用的超声装置产生的能量大小不足以将其分散开来。从图6中也可以看出,随着温度的升高,超声时间对石墨烯润滑油黏度的影响降低。温度升高,加剧了分散在润滑油中的纳米颗粒自身的布朗运动,导致石墨烯获得更高的能量,不易与周围纳米颗粒形成团聚体。为了减少由于较长超声时间导致的温度及粒径变化的影响,在研究石墨烯润滑油黏度随颗粒质量分数及温度变化的过程中,将超声作用时间设定为45 min,超声功率为600 W。
2.2.2 石墨烯质量分数对润滑油黏度的影响
石墨烯纳米颗粒质量分数增加,会在基液中形成较大尺寸的团聚体,纳米流体的黏度也随之增大。为了分析石墨烯润滑油纳米流体黏度随质量分数变化规律,分别测量质量分数为0.05%,0.1%,0.5%,1.0%时的润滑油黏度及相对黏度。石墨烯润滑油纳米流体黏度μnf及相对黏度(μnf/μbf)随质量分数的变化规律如图7所示。
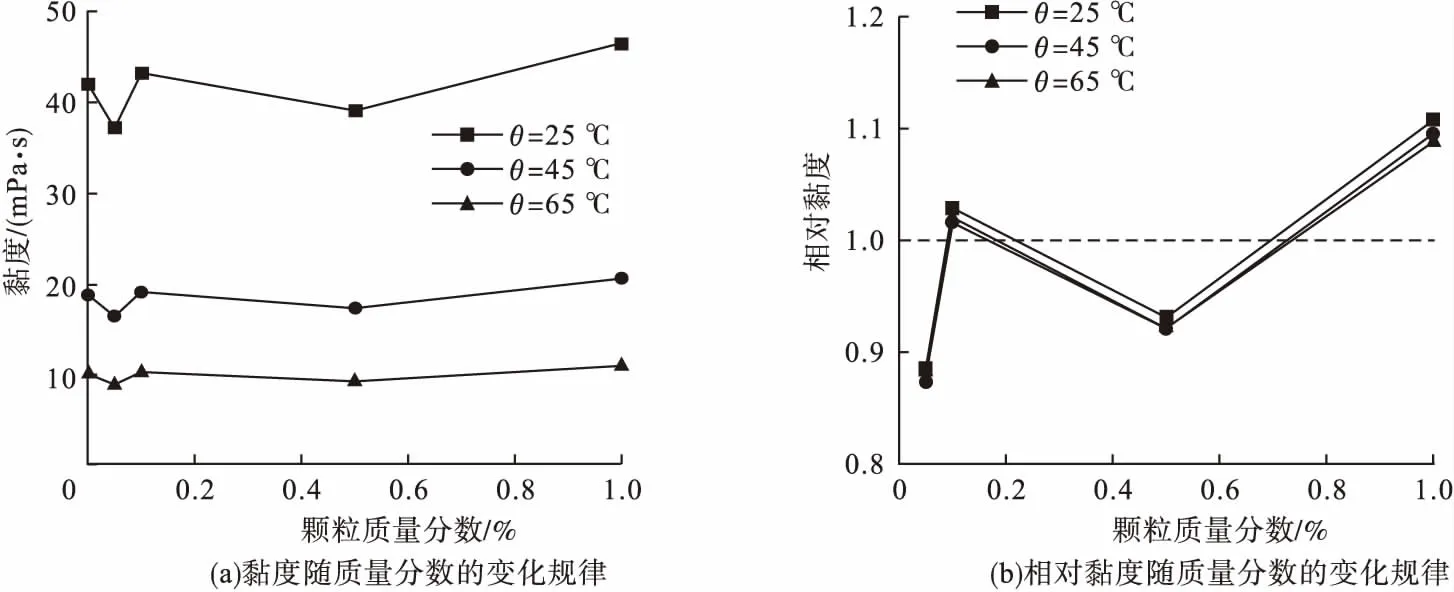
图7 石墨烯润滑油纳米流体黏度及相对黏度随质量分数的变化规律Fig.7 The viscosity and relative viscosity of graphene lubricating oil nanofluids with different mass fraction
由图7(a)可知,颗粒质量分数的增加与石墨烯润滑油黏度的变化存在非线性关系。随着颗粒质量分数的增加,石墨烯润滑油黏度出现不同程度的变化。其中,在质量分数为0.05%时,黏度最低,较基液相比降低11%;质量分数为1.0%时,石墨烯润滑油纳米流体的黏度达到最大值,较基液增加了10.48%。由图7(b)可知,在质量分数相同的情况下,温度变化对石墨烯纳米流体相对黏度的影响不大。
图8为石墨烯团聚体平均尺寸和黏度随颗粒质量分数变化规律。
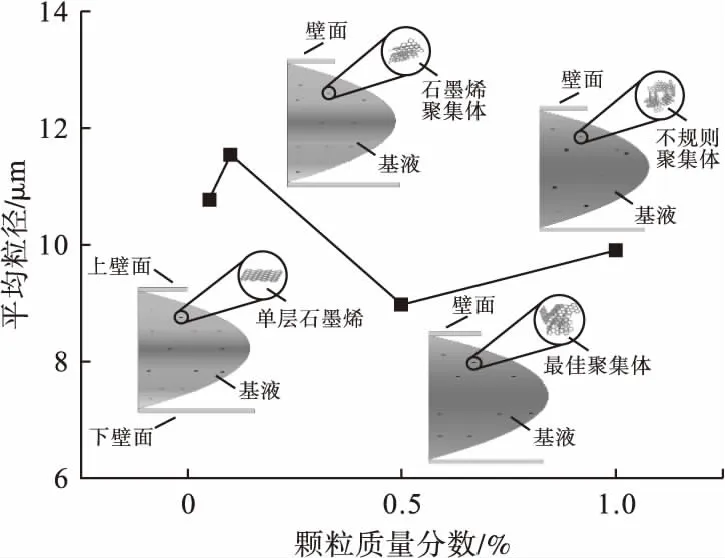
图8 石墨烯团聚体平均尺寸和黏度随颗粒质量分数变化规律Fig.8 The average size and viscosity of graphene agglomerates varying with particle mass fraction
由图可知,质量分数为0.5%的纳米流体中团聚体的平均尺寸最小,也验证了质量分数0.5%石墨烯润滑油黏度随质量分数的变化规律。
对于在质量分数为0.05%和0.5%时出现石墨烯润滑油黏度下降的现象,这是因为石墨烯纳米片为特殊的二维结构,具有较好的延伸性和较大的比表面积。图8还显示了石墨烯质量分数对黏度影响的机理。在润滑油中添加少量粒子(质量分数0.05%)后,石墨烯由于流体的流动性平铺在剪切层中,减少了层与层之间的阻力,从而降低了纳米流体的黏度[9];在基液中继续添加纳米粒子(质量分数0.1%),致使平衡结构被打破,石墨烯由于范德华相互作用开始逐渐聚集,形成尺寸更大的团簇,从而导致黏度上升;随着纳米粒子的继续增多(质量分数0.5%),石墨烯形成了最佳的团簇尺寸,与周围的液体分子范德华相互作用增加,减少了流体剪切层的数量,形成了一种新的平衡,再一次降低了纳米流体的黏度;当石墨烯添加量达到最大后(质量分数1.0%),纳米团簇由于其不规则的形状以及较大的尺寸,扰乱了润滑油的流动状态,增加了液体分子的无序度,导致石墨烯纳米流体的黏度增加。
2.2.3 温度对石墨烯润滑油黏度的影响
纳米流体黏度变化与温度具有强相关性。随着温度的升高,纳米流体的黏度与基础流体一样出现降低趋势,这是由于温度的升高会增加粒子的布朗运动及其平均速度,导致纳米粒子和基础流体分子间的吸引作用减弱[18]。在轴承中温度升高速度较快,容易造成润滑油的失效,进一步造成轴承内外圈及滚动体的磨损加剧,因此对于温度变化对石墨烯润滑油黏度的影响给予了重点关注。利用水浴加热装置对石墨烯润滑油进行恒温控制,通过调整预设水温(25 ℃、45 ℃、65 ℃)达到研究温度变化对石墨烯润滑油黏度影响规律的目的。图9为石墨烯润滑油纳米流体黏度随温度升高的变化规律。

图9 石墨烯润滑油纳米流体黏度随温度升高的变化规律Fig.9 The viscosity of graphene lubricating oil nanofluid with increasing temperature
由图9可知,不同质量分数的石墨烯润滑油纳米流体黏度随温度的升高全部出现降低的趋势。在25~45 ℃内,黏度下降幅度较大;在45~65 ℃内,黏度变化速度放缓。在更高的温度条件下,所有样品的黏度呈现归一化,这是由于较高的温度使润滑油的黏度出现较大的降低,纳米粒子的添加对黏度的影响减小。其中,质量分数为1.0%的石墨烯润滑油纳米流体的黏度在实验温度区间内变化最大,高达76.08%。从图中也可以看出,在实验温度范围内,质量分数为0.05%和0.5%的纳米流体黏度始终低于基础流体。
3 基于最小二乘法的石墨烯纳米流体黏度数学模型
通过对比实验数据与理论模型预测结果,可知传统的数学模型低估了石墨烯润滑油的黏度值。因此,笔者利用最小二乘法提出了一个可以计算石墨烯润滑油纳米流体黏度随超声时间、质量分数和温度变化的数学模型。最小二乘法主要通过最小化误差的平方以及最合适的数据匹配函数。由于石墨烯润滑油的黏度变化受基液类型的影响,因此首先提出了一个基液黏度随温度变化的函数。设石墨烯润滑油的基液黏度为μbf,则
(1)
(2)
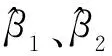

(3)
为了使Q达到最小,需要对Q进行求导,Q对两个待估参数的偏导数为
(4)
代入实验温度(298.15 K、318.15 K、338.15 K)及基础润滑油黏度数值,解得:
β1=-0.220 7,β2=78.05。
因此,基础油黏度变化与温度的关系为
(5)
其中,两个变量之间确定系数为0.979。同理,对于受到多种因素的影响石墨烯润滑油黏度,通过使用矩阵运算进行求解,表示为
(6)
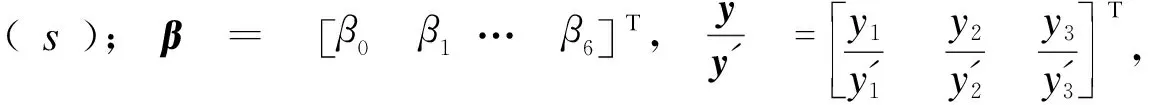

(7)
使得上述目标函数最小,即
y-XβT=0
(8)
求得:
βT=(XTX)-1XTy.
(9)
通过求解矩阵方程,推出石墨烯润滑油黏度随温度T、颗粒质量分数φ及超声时间t的变化的数学模型:
μnf/μbf=73.006 4-0.454 5T-17.815 4φ-
8.933×10-5t+7.171 9×10-4T2+3 516φ2+
5.720 2×10-9t2.
(10)
其中,298.15 K≤T≤338.15 K,0.05%≤φ≤1%,900 s≤t≤5 400s;R2=0.907 6。
为了验证笔者所提出的石墨烯润滑油黏度数学模型的准确性,对另外两种质量分数(0.25%,0.75%)石墨烯润滑油黏度模型预测值和实验值进行对比,如图10所示。由图可知,在实验范围内提出的数学模型可以较好地预测石墨烯润滑油黏度变化,尤其在高温条件下,预测值更加接近实验值。

图10 石墨烯润滑油黏度模型值和实验值对比Fig.10 The viscosity comparison between model and experimental results of graphene lubricating oil
4 结 论
(1)石墨烯的(002)峰较石墨出现右移,表明纳米层之间距离增加;质量分数为0.5%的石墨烯润滑油纳米流体分散稳定性表现最好,可以在无任何添加剂的情况下稳定20 d左右;通过流变试验确定了石墨烯润滑油在剪切范围内表现为牛顿流体。
(2)适当的超声时间可以有效降低石墨烯团聚体的尺寸大小,从而有效地降低石墨烯润滑油的黏度;但对于较高质量分数的样品,由于较强的范德华相互作用形成了较大尺寸的团聚体,需要更高的超声功率进行分散。
(3)石墨烯润滑油黏度随质量分数的变化规律并非总是线性增加的,在质量分数为0.05%和0.5%的样品中出现了纳米流体黏度低于基液黏度的现象,是因为石墨烯的特殊二维结构减小了流体层与层之间的摩擦和流体层数量。
(4)纳米流体的黏度与温度变化具有强相关性,随着温度的升高,所有石墨烯润滑油样品的黏度出现了不同程度的降低。
(5)笔者提出的数学模型式(10)与实验数据相比具有较好的一致性。
