圆钢管废弃钢渣混凝土短柱轴压承载力计算方法
2023-07-12路林翰任庆新张天贺
路林翰,任庆新,张天贺,梁 涛
(沈阳建筑大学土木工程学院,辽宁 沈阳 110168)
目前,我国钢渣年产生量超过1亿t,且累计堆存量不断攀升[1]。为提高钢渣的利用率、减少对土地资源的浪费和环境的污染,可将钢渣经过筛选、破碎、水洗等工序后,部分或完全代替天然粗骨料配制成钢渣混凝土。由于钢渣中含有的氧化钙与水发生反应使其体积膨胀[2],曲秀姝等[3-4]推荐将钢渣混凝土与钢管结合形成钢管钢渣混凝土,通过钢管的约束效应消除钢渣活性带来的不利影响。邢琳琳等[5-6]对比了钢渣骨料与天然骨料的物化特性,发现钢渣稳定性差、活性好等各种工程物化指标较天然骨料差,但其表面粗糙多孔且水泥的粘结力更高,可有效减轻其对承载力产生的负面影响,满足规范[7]对骨料的基本要求,可应用于结构化混凝土的配制。目前,对于废弃钢渣的研究重点主要针对骨料的分类及核心混凝土的力学性能两方面展开。在混凝土力学性能层面,王欣等[8]通过试验研究,量化了不同强度下核心混凝土钢渣细骨料取代率(0~30%)对混凝土力学和抗冲磨性能的影响,研究表明,混凝土的抗压强度和抗耐磨强度随钢渣细集料掺量的增加呈线性增长关系,且强度越低其增幅越大。王晨霞等[9]通过试验研究,量化了不同粗骨料取代率对混凝土力学性能的影响,研究表明,随钢渣取代率的增加,钢渣混凝土的峰值应力和峰值应变增加,且取代率为100%的钢渣混凝土弹性模量约为普通混凝土的1.2倍。
众多学者对钢渣骨料的结构化应用也进行了系列研究:石东升等[10-13]针对钢渣混凝土的轴压性能进行了试验研究,采用钢渣粗骨料取代率为主要参数,研究表明,钢渣混凝土和普通钢管混凝土的破坏模态无明显差异;钢渣等量取代碎石可提高混凝土的抗氯离子渗透、抗碳化和抗收缩性,且随着钢渣粗骨料取代率的增大,试件极限承载力和抗压强度呈先增后减的趋势,承载力最大降低幅度未超过16%;其中钢渣粗骨料替代率为25%和50%时,混凝土的早期和后期综合力学性能达到最佳。沈奇罕等[14]通过试验研究,量化了不同粗骨料取代率对椭圆截面钢管钢渣混凝土力学性能的影响,研究表明,随着钢渣骨料取代率的增加,试件的承载力提高2.0%~15.1%,刚度提升1.1%~16.8%,但其延性会随着钢渣取代率的增大而降低。
基于上述分析,笔者进行5组(共10个)圆钢管废弃钢渣混凝土短柱的轴压试验,获得试件的破坏模态和荷载-位移曲线;分析了钢渣骨料取代率和截面直径对极限承载力和延性系数的影响;基于规范[15-16]中轴压承载力计算公式进行极限承载力的预测,并对其精度进行分析,提出了圆钢管废弃钢渣混凝土短柱轴压承载力的计算方法,为圆钢管废弃钢渣混凝土轴压短柱的设计应用提供参考。
1 试 验
1.1 试验材料
圆钢管由厚度为3 mm的Q345B钢材经冷轧后形成,依据规范[17]对钢管的材性进行测试,得到钢材的屈服强度fy、抗拉强度fu、弹性模量Es和泊松比μs等性能指标,结果见表1。

表1 钢管材性试验结果Table 1 The test results of steel coupon
废弃钢渣取代率r为0、50%和100%三种,混凝土的配合比见表2。依据规范[18]测得立方体试块的抗压强度和棱柱体试件的弹性模量,参考规范[19]对立方体抗压强度实测值fcu进行修正计算得到fc,结果见表2。研究表明:随着钢渣骨料取代率的增加,混凝土的抗压强度和弹性模量呈下降趋势。取代率由0%增至50%、100%,立方体抗压强度分别降低3.7%和7.1%,弹性模量分别降低1.9%和3.6%。

表2 混凝土配合比和力学性能Table 2 The mixture ratio and mechanical properties of concrete
1.2 试件设计及制作
试验以钢渣骨料不同取代率(0、50%、100%)和不同截面直径(160 mm、180 mm、200 mm),设计并制作了5组共10个试件。Lü Wangqing等[20]建议钢管混凝土短柱轴压试件的长径比为3~3.5,因此,笔者试验中长径比取3,试件相关参数见表3。
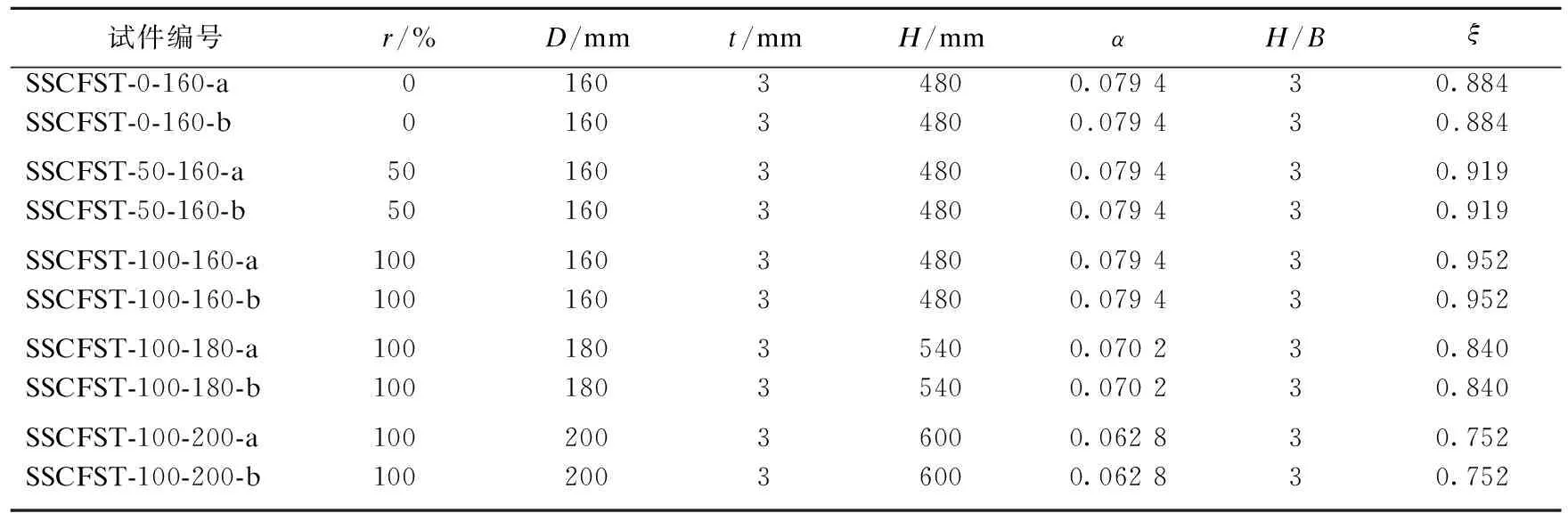
表3 试件参数Table 3 The parameters of specimens
试件由端板、钢管及核心混凝土三部分组成。端板采用厚度20 mm的钢板,焊接前将钢管两端打磨光滑,焊接过程中将下端板与一端钢管焊接完成后进行浇筑核心混凝土,浇筑过程中边浇筑边捣实,直至略微溢出。混凝土养护至28 d,随后打磨至钢管口齐平后将上端板与钢管焊接完成。
1.3 试件加载装置及测量方式
试验在5 000 kN多功能试验机下进行,为模拟圆钢管钢渣混凝土短柱铰接支撑条件,试件两端所用的加载板均采用平板铰。试验前在试件端板处设置位移计,试验加载及量测示意图如图1所示。
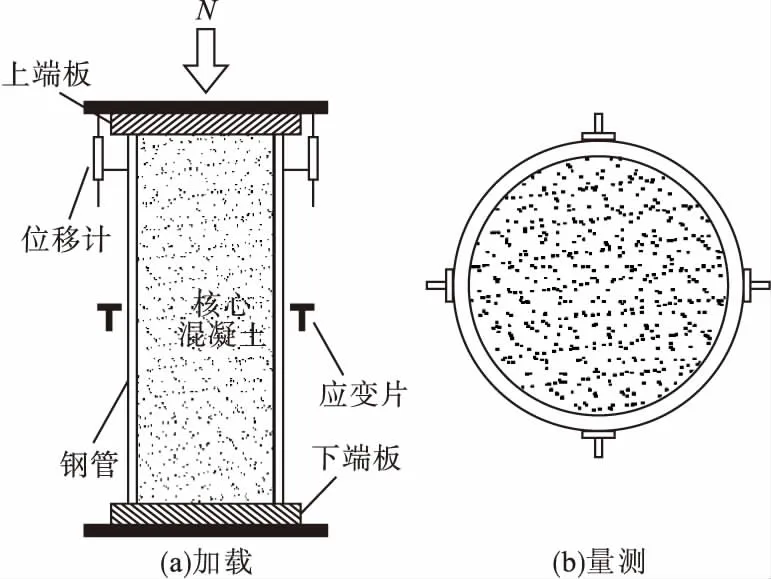
图1 试验加载及量测示意图Fig.1 The schematic diagram of test loading and measurement
加载前,试件中心尽量与加载板中心重合,保证试件发生轴压破坏。正式加载前进行预加载,预加载值约为峰值荷载的10%,检查试验仪器是否运行正常。正式加载时,峰值荷载前采用荷载分级加载的方式:弹性阶段每级荷载增量值为100 kN,进入屈服阶段后每级加载减少至50 kN,每级加载的持续时间为1 min;试件达到峰值荷载后,参考位移计读数来控制分级加载,每级位移增量为1~3 mm,当试件位移达到柱高的2.5%时,停止加载。
2 试验结果及分析
2.1 试验现象
试件的最终破坏形式如图2所示。由图可知,圆钢管废弃钢渣混凝土短柱轴压构件的破坏模态与钢管普通混凝土基本一致,外钢管的鼓曲一般发生在试件靠近中部的位置。试件在加载初期处于弹性阶段,荷载和位移变化均较小,荷载-位移曲线呈线性变化。当试件进入弹塑性阶段,位移逐渐增加,钢管逐渐向外发生轻微的鼓曲,隐约可以听到试件内部混凝土的窸窣破碎声。试件的承载力达到峰值荷载后,位移增长加速,钢管局部出现明显鼓曲且试件承载力逐渐下降。

图2 试件的最终破坏形式Fig.2 The final failure mode of the specimens
2.2 荷载-位移曲线
试验中测得各个试件的荷载-位移(N-Δ)曲线如图3所示。由图可知,所有试件均呈现出了五阶段受力状态,即弹性阶段、弹塑性阶段、强化阶段、下降阶段、平稳阶段。试件受压前期核心混凝土和钢管分别受力,钢管未对核心混凝土产生横向约束,位移呈线性增长。荷载增至极限荷载的60%~70%,曲线斜率逐渐减小,核心混凝土变形不断增加且出现微裂缝,但由于钢管对核心混凝土的约束作用,试件承载力仍缓慢增加。达到峰值荷载后,试件逐渐发生破坏,核心混凝土处于三向应力状态,试件承载力下降缓慢且位移显著增加。


图3 各组试件的荷载-位移曲线Fig.3 The load-displacement curves of each specimen group
图3(a)~图3(c)为不同钢渣取代率试件的荷载-位移关系曲线。由图可见,圆钢管废弃钢渣混凝土轴压短柱荷载-位移曲线的离散性与普通圆钢管混凝土短柱相似,且试件达到峰值荷载时所对应的位移值均在2.3 mm左右,即钢渣骨料取代率对试件达到峰值荷载时所对应的位移量影响较小。
图3(c)、图3(d)、图3(e)为不同截面直径试件的荷载-位移关系曲线,试件峰值荷载所对应的位移值随截面尺寸的增加而增加,这是由于截面直径增加提高了试件的承载能力,推迟了极限状态的发生。
2.3 极限承载力分析
2.3.1 钢渣骨料取代率对极限承载力的影响
圆钢管废弃钢渣混凝土轴压短柱承载力随钢渣骨料取代率的变化如图4所示。由图可知,钢渣骨料的掺入对试件承载力的影响较小,可以忽略,钢渣骨料取代率从0提升至50%、100%,构件的承载力分别平均提高3.4%和降低1.4%,变化幅度均在5%以内。分析原因,不同取代率时钢渣混凝土的抗压强度最大相差7.1%,将其引入到钢管中,进一步降低了钢渣取代率的影响。基于上述结果,可认为圆钢管废弃钢渣混凝土轴压短柱的承载力可以满足结构的使用要求。
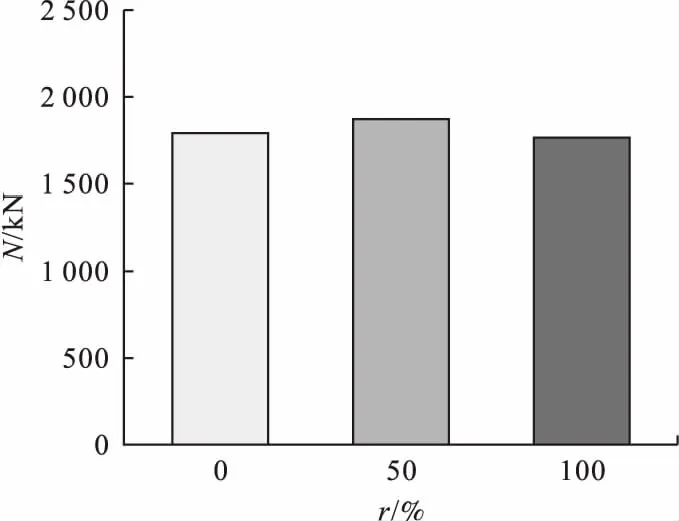
图4 取代率对承载力的影响Fig.4 The effect of replacement ratio on axial compressive strength
2.3.2 截面直径对极限承载力的影响
对3组不同截面直径的试件进行极限承载力对比分析如图5所示。由图可知,圆钢管废弃钢渣混凝土轴压短柱的极限承载力随截面直径的增加而增加。截面直径180 mm试件的极限承载力较截面直径160 mm试件的极限承载力增大20.4%,截面直径200 mm试件的极限承载力较截面直径160 mm的极限承载力增大54.6%,基本呈现线性增长趋势。这是由于截面直径的增加导致径厚比的增加,降低了钢管对核心混凝土的约束作用,同时,核心混凝土和钢管对承载力的贡献比例发生改变,受钢管约束的核心混凝土面积增多,使试件整体的承载力提高。
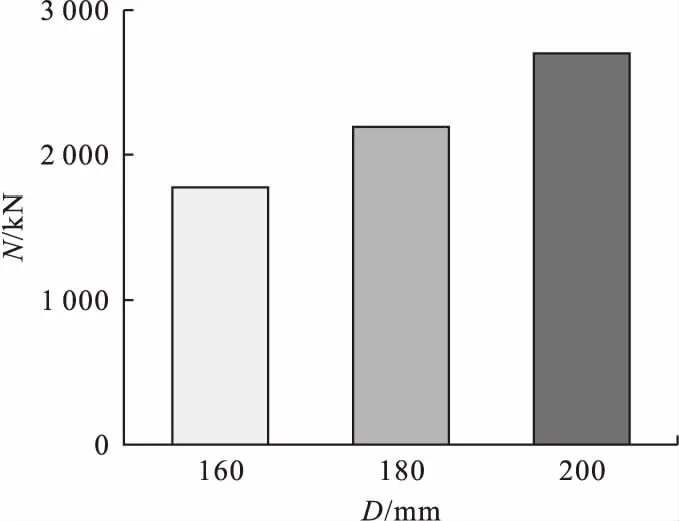
图5 截面直径对承载力的影响Fig.5 The effect of section size on axial compressive strength
2.4 延性分析
2.4.1 钢渣骨料取代率对延性的影响
不同钢渣骨料取代率对试件延性系数的影响如图6所示。由图可知,钢渣骨料取代率由0提升至50%、100%,试件的延性系数分别提升了12.4%和39.5%,约束效应系数分别增加了3.8%和7.7%。

图6 取代率对延性系数的影响Fig.6 The effect of replacement ratio on ductility coefficient
2.4.2 截面直径对延性的影响
图7为不同截面直径对试件延性系数的影响,截面直径由160 mm增加至180 mm、200 mm,试件的延性系数分别降低了21.7%和37.5%,约束效应系数分别降低11.8%和21.0%。笔者对文中数据进行线性拟合,如图8所示。试验中的延性系数和约束效应系数也呈正相关,约束效应系数和延性系数随钢渣骨料取代率的增加而增大,随截面直径的增大而减小。即外钢管对核心混凝土的约束效应越强,试件的延性性能则越好。
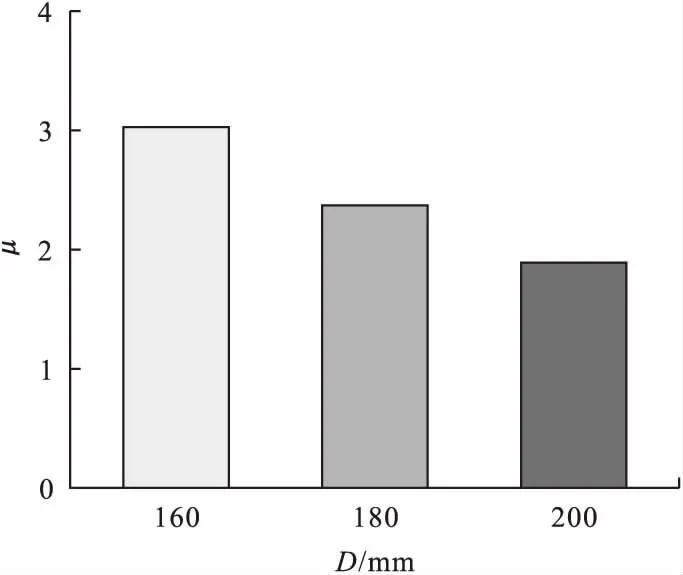
图7 截面直径对延性系数的影响Fig.7 The effect of section size on ductility coefficient
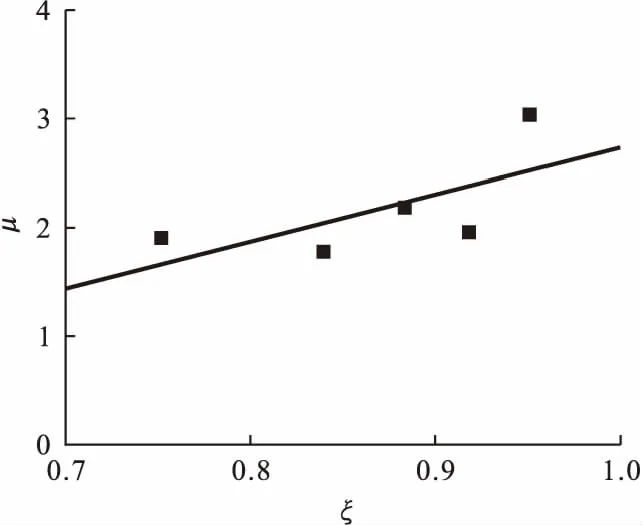
图8 延性系数-约束效应系数关系曲线Fig.8 The relationship between ductility coefficient and hoop coefficient
3 承载力计算方法
3.1 计算结果与试验结果对比
根据《钢管混凝土结构设计规范》(GB 50936—2014)[17]和《钢管再生混凝土技术规程》(TCECS 625—2019)[18]中的轴压短柱承载力计算公式对圆钢管废弃钢渣混凝土短柱的轴压承载力进行理论计算,承载力理论计算结果与试验值的对比结果见表4。基于规范中式(1)[17]、式(2)[17]与式(3)[18]的误差平均值分别为 0.97,1.04,0.91,方差分别为0.03,0.04,0.05,其计算结果中部分计算值较试验值相比误差大于10%且小于15%,可以有效地预测圆钢管废弃钢渣混凝土短柱轴压承载力。

表4 理论计算值与试验值的对比Table 4 The comparison of theoretical calculated values and experimental results
(1)
N2=Ascfsc.
(2)
其中,fsc=(1.212+Bξ+Cξ2)fc;B=0.176fu/213+0.974;C=-0.104fc/14.4+0.031。
N3=Ascfsc=Asc(1.14+1.02ξ)fc.
(3)
式中:fc为混凝土轴心抗压强度;Ac为混凝土横截面面积;Asc为钢管混凝土柱横截面面积;fsc为实心钢管混凝土抗压强度;fu为钢材抗拉强度;ξ=fyAs/fcAc,为套箍系数。式(1)、式(2)来源极限平衡理论;式(3)来源统一强度理论。
3.2 承载力修正计算
图9(a)为圆钢管废弃钢渣混凝土短柱轴压承载力理论计算结果的散点图,通过引入修正系数μ和截距修正量β,进行线性拟合,以改变表中理论计算公式的参数,得到N与N0的关系,式(4)为修正后的计算承载力。

图9 承载力计算值与试验值对比Fig.9 The comparison between calculated values and tested results of bearing capacity
N=μN0+β.
(4)
式中:N为承载力修正计算值;N0为规范承载力计算值;μ为修正系数;β为截距修正量。
表5为实验数据参数拟合后的修正结果,修正后的理论计算公式精确度较高,其判定系数均大于0.97,平均误差均小于10%,相比式(2)和式(3),式(1)的计算结果处于安全范围且精确度较高,因此可以使用式(1)对圆钢管废弃钢渣混凝土短柱进行计算。

表5 修正参数拟合值Table 5 The fitting values of parameter after correction
4 结 论
(1)钢渣骨料取代率的变化没有改变圆钢管废弃钢渣混凝土短柱的破坏模态,构件承载力的差值在5%以内。
(2)构件的承载力随截面直径的增加而增大且不会改变试件的破坏模态;截面直径180 mm的圆钢管废弃钢渣混凝土短柱的极限承载力较截面直径160 mm试件的极限承载力提高20.4%,截面直径200 mm试件的极限承载力较截面直径160 mm试件的极限承载力提高54.6%;钢管废弃钢渣混凝土的延性性能与约束效应系数呈正相关。
(3)基于规范[15-16]中圆钢管混凝土轴压承载力的计算方法,笔者引入修正系数和截距修正量进行拟合修正,提出了圆钢管废弃钢渣混凝土短柱轴压承载力的计算方法,试件承载力计算值与试验值吻合良好,计算结果偏于安全,可为工程应用提供理论参考。
