双肢U形拼合冷弯薄壁型钢箱梁受弯性能试验

2023-07-12周弘昊

沈阳建筑大学学报（自然科学版） 2023年3期

黄远,周弘昊

(湖南大学土木工程学院,湖南长沙 410082)

由冷弯薄壁型钢基本构件组合而成的拼合截面构件被广泛应用于冷弯型钢结构楼盖承重体系中。拼合构件克服了单肢构件因质心和剪心不重合而容易扭转屈曲的问题。同时,为了方便线路、管道系统在构件中穿越,经常在梁腹板中开孔洞,孔洞的存在将影响构件中应力的重分布,影响了构件的屈曲特征和屈曲承载能力。

C.D.Moen等[1-3]针对腹板开孔构件受弯承载力计算方法展开了一系列研究,提出了考虑开孔影响的直接强度法,但该方法仅针对单肢构件。B.Beshara和L.S.Serrette[4-5]通过试验指出在偏心荷载作用下,拼合箱梁的受弯承载力小于单个构件承载力之和。P.Sultana等[6]提出冷弯薄壁拼合箱梁惯性矩和受弯承载力可以按单个基本构件简单叠加得到。L.Xu等[7]建议在偏心作用下,双肢拼合箱梁受弯承载力应在《北美冷弯型钢规范》(AISI S100—16)规定的单个构件承载力叠加基础上乘以0.9的折减系数。石宇等[8]对由C形和U形冷弯薄壁型钢拼合而成的箱梁进行受弯试验研究,指出由于存在拼合效应,拼合箱梁受弯承载力大于各单肢承载力之和,并提出了抗弯模量折减法用于计算拼合箱梁承载力。Y.L.Li[9]研究了C形和U形拼合箱梁梁在强、弱轴纯弯曲作用下的受力性能,结果表明,箱梁拼合效应确实存在,但由于C形梁和U形梁不能同时达到峰值荷载,因此建议拼合箱梁绕强轴弯曲时的弯矩承载力为各构件承载力总和的90%。L.Wang等[10-11]对43根10种横截面尺寸和不同孔径的组合箱梁进行了四点弯曲试验研究及有限元分析,结果表明,《北美冷弯型钢规范》(AISI S100—16)[12]中直接强度法对于开孔箱梁计算结果偏于保守。

目前,国内外针对冷弯单肢腹板开孔受弯构件研究理论较多[13-16],而对双肢拼合腹板开孔箱梁的研究较少。同时,各国规范[12,17]中关于冷弯薄壁型钢受弯构件的设计公式针对的是单肢构件,而对于双肢拼合构件,《北美冷弯型钢规范》(AISI S100—16)建议拼合构件受弯承载力可按单肢构件承载力之和进行叠加。我国现行《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ 227—2011)[18]中建议双肢抱合箱型截面梁受弯承载力可将翼缘厚度叠加后按部分加劲等效成整体箱梁进行计算。石宇等[8]指出该方法在拼合箱梁翼缘宽厚比较大时,计算结果将偏于不安全。鉴于上述情况,笔者通过试验探究了双肢U形拼合冷弯薄壁型钢箱梁的受弯破坏过程,研究了腹板开孔比和螺钉间距对拼合箱梁受弯性能的影响,同时对《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ 227—2011)和《北美冷弯型钢规范》(AISI S100—16)中关于拼合箱梁受弯承载力计算方法进行验证。结果表明当腹板开孔较大时会显著降低拼合箱梁受弯承载力,采用《冷弯薄壁型钢结构技术规范》(GB 50018—2002)计算单肢截面承载力后再简单叠加后得到的预测结果与试验值最为接近。

1 试验

1.1 试件设计

双肢U形拼合冷弯薄壁型钢箱梁由两根单肢U形钢通过自攻螺钉ST4.8×19连接而成,试件长度L=1600 mm、试件厚度t=1.5 mm、翼缘宽度B=50 mm,试件截面形式如图1所示。试件截面尺寸参考《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ 227—2011)中冷弯型钢开洞楼板洞口周围设置的拼合箱型截面梁。共对12个试件进行四点弯曲试验,试件参数见表1。

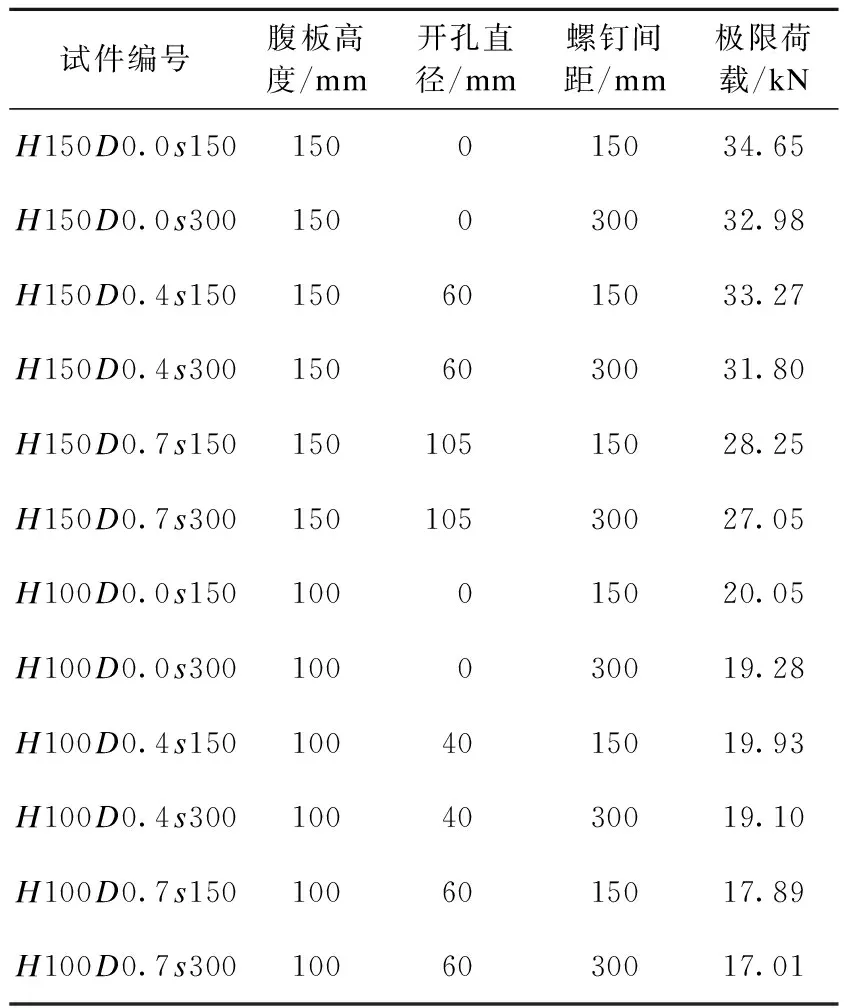
表1 试件参数Table 1 Specimen parameter table

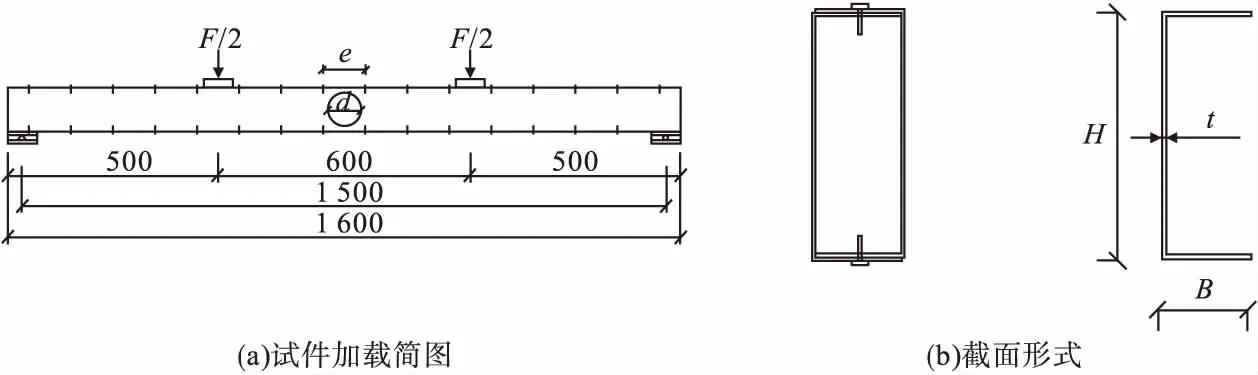
图1 试件截面和加载形式Fig.1 Section form and loading method of the specimen

笔者选取开孔比d/H为0.4和0.7,螺钉间距为150 mm和300 mm,进而研究不同参数对拼合箱梁受弯性能的影响。为了防止试件加载时发生局部屈曲,在加载点和支座处箱梁内部分别设置了U60×50×1.5的加劲肋,外部设置了型号为C100×50×1.5×12的加劲肋。

钢材材性试验根据《金属材料拉伸试验第1部分:室温试验方法》(GB/T 228.1—2010)[19]的规定,从U形构件腹板平行于轧制方向切取3个板状试件进行拉伸试验。钢材的屈服强度为284 MPa,极限强度为355 MPa,断后伸长率为38%,弹性模量为2.0×105MPa。

1.2 试件装置及测点布置

试验装置如图2(a)所示。采用10 t液压千斤顶进行加载,通过工字型钢分配梁将荷载均匀分配到箱梁加载点处,加载点间距600 mm,试件两端简支。同时为了防止试件发生平面外屈曲,在加载点附近设置三脚架夹具(见图2(b))。正式加载时采用分级加载制度,每级荷载取为预估最大荷载的20%,每一级加载完成后持荷2 min,进行数据采集及观测。当荷载下降到最大荷载的85%时,为安全考虑,停止加载。

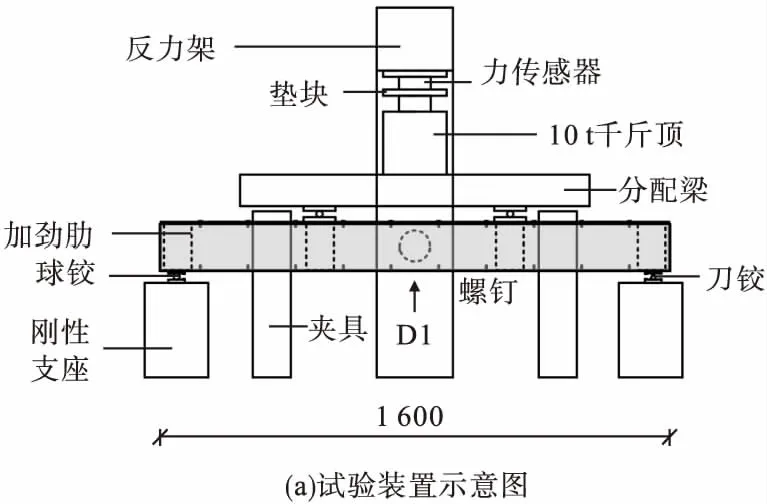
图2 试验装置及量测布置Fig.2 Test set-up and measuring arrangement

在箱梁跨中底部中心位置设置1号位移计D1,用来测量拼合箱梁跨中竖向位移。试件应变片布置如图2(c)所示,在试件上翼缘跨中沿长度方向布置3个应变片,应变片间距150 mm,其中s2号应变片位于跨中截面正上方翼缘表面;两侧腹板沿高度方向对称布置6个应变片,下翼缘跨中布置1个应变片,所有数据的采集由静态电阻应变箱完成。

2 结果与分析

2.1 试验现象

试验结果表明,腹板开孔尺寸对试件的破坏模式影响较大,不同开孔尺寸下试件典型破坏模式如图3所示。所有试件都发生平面内受弯破坏,破坏模式表现为翼缘与腹板发生局部屈曲而破坏,所有试件破坏时螺钉保持完好。

图3 试件破坏特征Fig.3 Failure modes of specimens

对于未开孔和开孔比为0.4的试件,当加载到极限荷载70%左右时,试件纯弯段靠近加载点处的翼缘出现局部屈曲,继续加载至极限荷载的80%左右时,跨中开孔上方腹板处出现局部屈曲。当达到极限荷载时,靠近加载点处翼缘局部屈曲变形突然增大,试件随之丧失承载力。试件跨中处局部屈曲发展缓慢,试件破坏状态是加载点处的翼缘出现局部屈曲变形较大而丧失承载力。

对于开孔比为0.7的试件,当荷载达到极限荷载70%左右时,试件纯弯段靠近加载点处的翼缘首先出现局部屈曲,继续加载至最大荷载的80%左右时,试件跨中翼缘和开孔上方腹板出现局部屈曲,表现为翼缘凸起和开孔上方腹板外扩。继续增大荷载,试件跨中翼缘和腹板变形逐渐增大,当达到最大荷载时,试件跨中翼缘和孔洞上方腹板屈曲变形突然增大,同时荷载迅速下降,试件丧失承载力,破坏呈脆性趋势。试件的最终破坏状态表现为跨中处翼缘和腹板发生局部屈曲破坏。

2.2 荷载-位移曲线

双肢U形拼合冷弯薄壁箱梁荷载-位移曲线如图4所示。位移测量点为试件跨中截面下翼缘中心处。

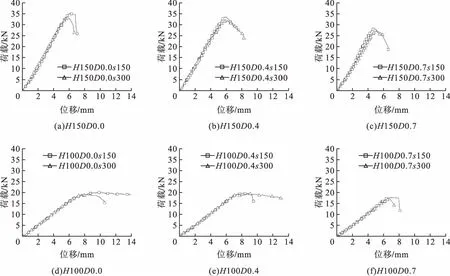
图4 试件荷载-位移曲线Fig.4 Load-displacement curves of specimens

由图4 可以看出,螺钉间距由150 mm增大到300 mm时,荷载-位移曲线斜率基本一致,改变螺钉间距对拼合箱梁初始刚度影响较小。加载初期,荷载-位移曲线呈线性关系增加,试件处于弹性变形阶段,拼合后的箱梁在螺钉约束下能共同变形承受外力。随着荷载增加,试件上翼缘处出现局部屈曲,试件整体刚度下降,荷载-位移曲线出现非线性段。继续加载到最大荷载后,上翼缘和腹板局部屈曲变形突然增大,试件丧失承载能力,荷载迅速下降。试件H100D0.0s150和H100D0.4s300在达到极限荷载后荷载下降缓慢,这是因为实际加载过程中达到最大荷载后没有继续加压,导致试件破坏时塑性变形发展缓慢,荷载-位移曲线比较平滑。

各试件极限承载力随螺钉间距变化关系如图5所示。从图中可以得出,腹板高度为150 mm的试件,螺钉间距由150 mm增加到300 mm时,开孔比为0、0.4和0.7时极限承载力分别下降了4.8%、4.4%和4.2%;腹板高度为100 mm的试件,螺钉间距由150 mm增加到300 mm时,开孔比为0、0.4和0.7时极限承载力分别下降了3.8%、4.2%和4.9%。拼合箱梁的破坏模式表现为上翼缘发生局部屈曲而分离,增大螺钉间距导致拼合箱梁的拼合效应减弱,在上翼缘达到屈服荷载后由于螺钉的约束作用减弱,使得拼合后的承载力略微降低。

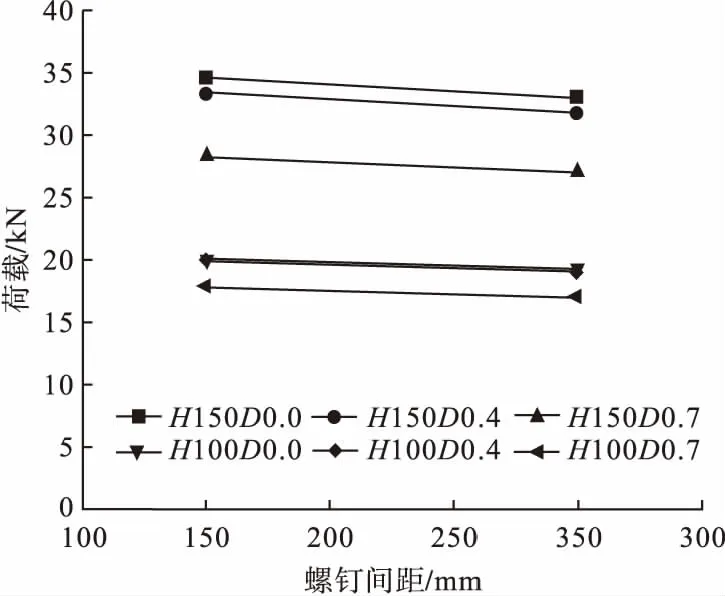
图5 不同螺钉间距极限承载力对比Fig.5 Comparison of ultimate bearing capacity with different screw spacing

各试件极限承载力随腹板开孔比变化关系如图6所示。从图中可以得出,腹板高度为150 mm的试件,当螺钉间距为150 mm时,开孔比为0.4和0.7的试件与未开孔试件相比,极限承载力下降了1%和18%;当螺钉间距为300 mm时,极限承载力下降了0%和18%。腹板高度为100 mm的试件,当螺钉间距为150 mm时,开孔比为0.4和0.7的试件与未开孔试件相比,极限承载力下降了1%和11%;螺钉间距为300 mm时,极限承载力下降了1%和12%。由此可知,对于双肢拼合腹板开孔冷弯箱梁,当开孔比为0.4时,腹板开孔对箱梁极限承载影响很小,可以忽略;当开孔比为0.7时,孔洞的存在会明显降低箱梁极限承载力。同时,对于腹板开孔比为0.7的试件,极限荷载对应的峰值位移明显低于未开孔试件,呈脆性破坏趋势,腹板开孔较大时会降低拼合箱梁的延性。

图6 不同开孔比下极限承载力对比Fig.6 Comparison of ultimate bearing capacity with different opening ratios

2.3 荷载-应变曲线

腹板高度为150 mm的试件荷载-应变曲线如图7所示。应变片s2位于受压上翼缘,应变片s4位于腹板受压侧,应变片s5位于腹板形心轴上,应变片s6位于腹板受拉侧,应变片s7位于下翼缘。

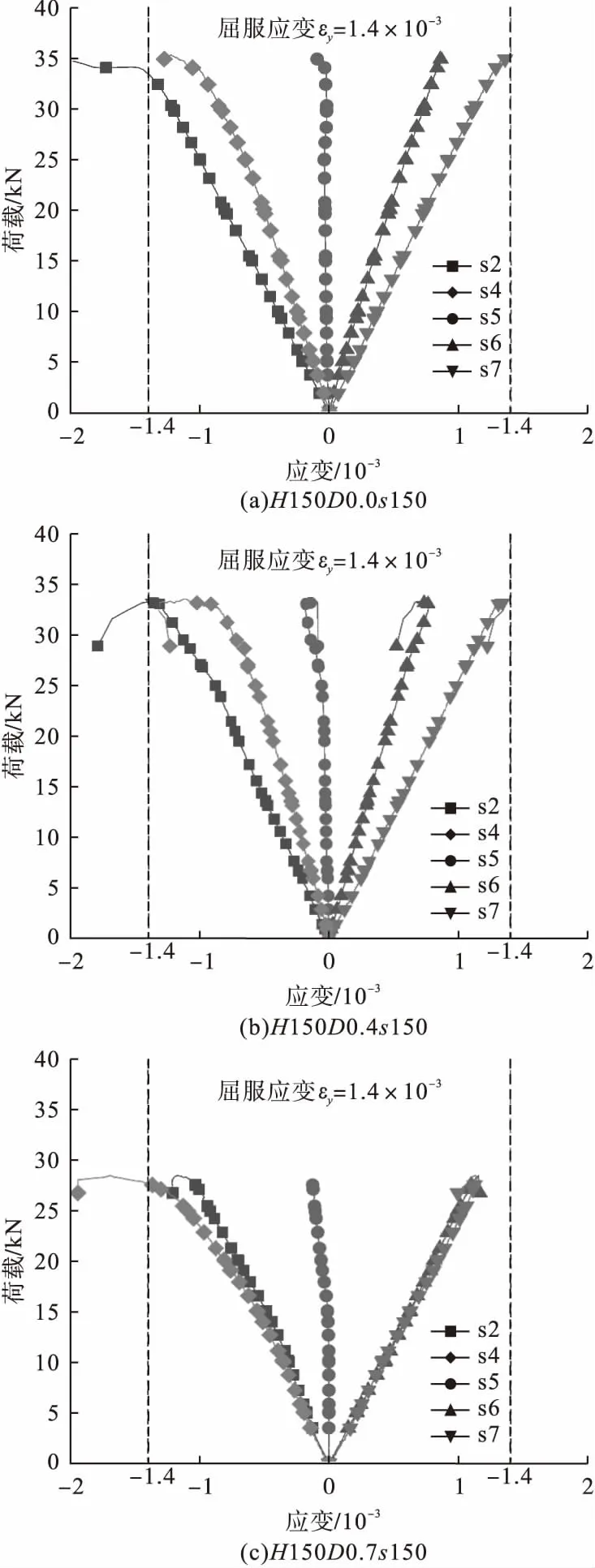
图7 试件荷载-应变曲线Fig.7 Load-strain curves of specimens

从图7可以看出,对于试件H150D0.0和H150D0.4,加载初期,试件处于弹性阶段,荷载-应变曲线呈线性增长,距离中性轴越远的应变片应变越大。根据试件材性试验结果可知,当应变达到1.4×10-3左右时,材料达到屈服;加载过程中试件上翼缘率先达到屈服,对应的应变片s2应变曲线斜率发生变化,应变迅速增加。继续加载,应变片s2荷载-应变曲线接近于水平,试件达到极限荷载进入破坏阶段,而受拉区腹板和翼缘在加载过程中未发生屈曲,应变片s6和s7荷载-应变曲线基本保持线性变化。

对于试件H150D0.7,应变变化相较于未开孔试件有所区别,由于开孔较大导致跨中腹板受力面积较小,应力集中明显,所以在加载过程中,腹板上方应变片s4应变增量大于上翼缘应变片s2。随着荷载继续增加,腹板开孔上方率先出现屈服,应变片s2斜率发生变化,荷载-应变曲线接近水平,试件进入破坏阶段。受拉区腹板和翼缘应变片s6和s7的荷载-应变曲线保持线性变化。

2.4 截面应变分布

图8 为6组典型试件在不同加载时期截面高度不同位置应力分布图,图中纵坐标表示应变片距离中性轴的距离,以受压区为正。荷载分别取Pmax/3、2Pmax/3和Pmax,其中Pmax为试件极限承载力。从图中可以得出,对于未开孔试件和开孔比为0.4的试件,各点应变连线基本保持在一条直线上,拼合后的截面基本满足平截面假定;对于开孔比为0.7的试件,因腹板开孔较大导致腹板边缘应力集中明显,出现腹板处应变大于翼缘应变的情况,难以满足平截面假定。

图8 试件跨中截面应变分布图Fig.8 Strain distribution diagram of specimen mid-span section

3 拼合箱梁承载力计算方法

图9为不同计算方法下拼合箱梁受弯承载力结果对比。方法一:按照《冷弯薄壁型钢结构技术规范》(GB50018—2002)计算两单肢构件受弯承载力,然后简单叠加得到拼合箱梁承载力,计算结果用M1表示;方法二:按照《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ 227—2011)中的建议,当拼合截面翼缘有可靠连接时等效成整体箱梁来计算受弯承载力,计算结果用M2表示;方法三:按照《北美冷弯型钢规范》(AISI S100—16)中直接强度法计算两单肢截面承载力后进行简单叠加得到拼合截面承载力,计算单肢截面时考虑开孔影响,计算结果用M3表示,其中单肢截面承载力按照直接强度法进行计算,同时考虑开孔影响[20];方法四:按照石宇等[5]针对拼合箱梁提出的折减模量法,计算结果用M4表示。

图9 不同计算方法结果与试验值对比Fig.9 The results of different calculation methods were compared with the experimental values

(1)

(2)

式中:Mnl为局部屈曲极限弯矩;Mne为整体屈曲极限弯矩;Mcrl局部屈曲临界弯矩,可以根据有限条软件CUFSM直接计算得到。

所有试验数据来源于文中试验及文献[10]。其中方法一没有针对腹板开孔构件受弯承载力的计算方法,由2.2小节试验结果分析可知,当腹板开孔比等于0.4时,腹板开孔对拼合箱梁受弯承载力影响不大,因此对开孔比小于0.4的试件受弯承载力可按照未开孔试件计算。

由图9 可以得出,按照方法一计算单肢截面承载力后,再简单叠加得到的预测结果与试验值最为接近,误差在10%以内,平均值为1.05,标准差为0.03。按照方法三计算单肢截面承载力后简单叠加的方法整体上偏于保守,最大误差接近30%,平均值为1.14,标准差为0.07。两种方法都偏于保守,这是由于两种方法未考虑拼合效应,只是简单的叠加两单肢承载力得到拼合截面承载力。而方法二计算得到拼合箱梁受弯承载力试验结果与预测结果比值平均值为0.85,标准差为0.03,预测值偏大,造成这一误差的原因是上翼缘自攻螺钉并不能完全约束两单肢构件共同变形,方法二翼缘厚度直接叠加计算忽略了两单肢构件上翼缘分离这一影响,导致计算结果偏大。方法四预测结果平均值为0.98,标准差为0.03,但该方法适用于钢材强度介于Q235和Q345之间的箱梁。