履带式甘蔗收割机坡道行驶稳定性分析与仿真*

2023-07-11李锦新武涛刘庆庭徐凤英任甲辉黄俊杰

中国农机化学报 2023年6期

李锦新，武涛，刘庆庭，徐凤英，任甲辉，黄俊杰

(1.华南农业大学工程学院,广州市,510642;2.中山市技师学院汽车系,广东中山,528400)

0 引言

甘蔗是我国重要的糖料作物,其种植区域主要分布在广西、云南、广东、海南等地,其中广西、云南甘蔗种植面积占全国70%以上[1-3]。广西甘蔗种植地形主要为6°以下的缓坡地(占蔗区面积76.15%),其余的分布于丘陵地(占蔗区面积23.85%)[4];云南甘蔗种植地形主要为6°以下的缓坡地(占蔗区面积30.5%)与6°～15°的丘陵地(占蔗区面积32.1%)[5]。以上两省的甘蔗种植地以缓坡地和丘陵地为主,甘蔗收割机在行驶时会发生侧翻危险,因此亟需对甘蔗收割机坡道行驶性能进行分析。

甘蔗收割机有轮式和履带式,轮式收割机机动性好,适宜平坦路况行驶,履带式收割机通过性好,适宜在丘陵山区使用。国内外学者对车辆坡道行驶性能有广泛研究：Yamada等[6]研制出叶片式履带底盘,并通过理论和试验分析坡道行驶性能。Gao等[7]对履带式攀岩机器人的坡道行驶性能和抗倾翻性能进行了研究。Sun等[8]研制了一种在联合收割机上可调升降的履带底盘,通过调平技术来控制底盘高度,以防止车辆倾翻危险。刘泽旭等[9]通过对轮式与三角履带式集材机爬坡过程进行受力分析,得出两款集材机牵引力、最大爬坡度、爬坡速度和消耗的表达式。刘大为等[10]针对履带车辆坡地作业时存在爬坡性能变成问题,提出了一种采用三连杆变形机构,通过对变形机构自由度计算,确定变形与未变形状态下履带车辆的爬坡性能。李艳萍等[11]对油茶抚育机的爬坡性能进行试验,得出最佳的重心位置和爬坡速度,提高了爬坡稳定性。王品健等[12]针对履带车辆行驶时驱动轮转速与路面类型的差异,研究履带车辆在坡面行驶时转速与路面对爬坡性能的影响。潘冠廷等[13]对小型山地履带拖拉机爬坡越障性能进行分析,得出增大越障速度和质心—支重轮距、减小坡度角和质心高度均可提高山地拖拉机的爬坡越障性能。陈继清等[14]对小型绿篱修剪机履带底盘越障性能进行分析,得出机器最大纵向上坡角、最大越障高度。上述学者研究的对象为机器人或其他履带底盘,对于履带式甘蔗收割机坡道行驶性能缺乏研究。

目前履带式收割机有两履带式和四履带式,两履带式具有与地貌接触面积大、抓地力强优点,四履带式具有质量轻、振动小、高机动性等优点[15-19]。两履带和四履带结构各有优点,本文以华南农业大学自主研发的两履带甘蔗收割机(以下简称A机)和四履带甘蔗收割机(以下简称B机)为研究对象,以极限倾翻角为评价指标,进行坡道行驶稳定性理论分析。由于坡道行驶物理试验存在倾翻危险,因此采用仿真方法分析两机的坡道行驶稳定性,为甘蔗收割机底盘进一步优化设计提供参考。

1 整机结构与工作原理

A机与B机都包括发动机、输送臂组件、履带组件、车体组件等几部分。整机结构如图1所示。两机的基本结构参数如表1所示。

表1 两机基本结构参数Tab.1 Basic structural parameters of two machines

(a) A机

A机与B机结构上的主要差别：A机输送臂位于整机后部,输送臂与旋转平台连接,可绕平台水平旋转±90°(图2),蔗段可通过输送臂运送至田间运输车上,B机输送臂为固定式,蔗段通过输送臂运送至集蔗箱内。

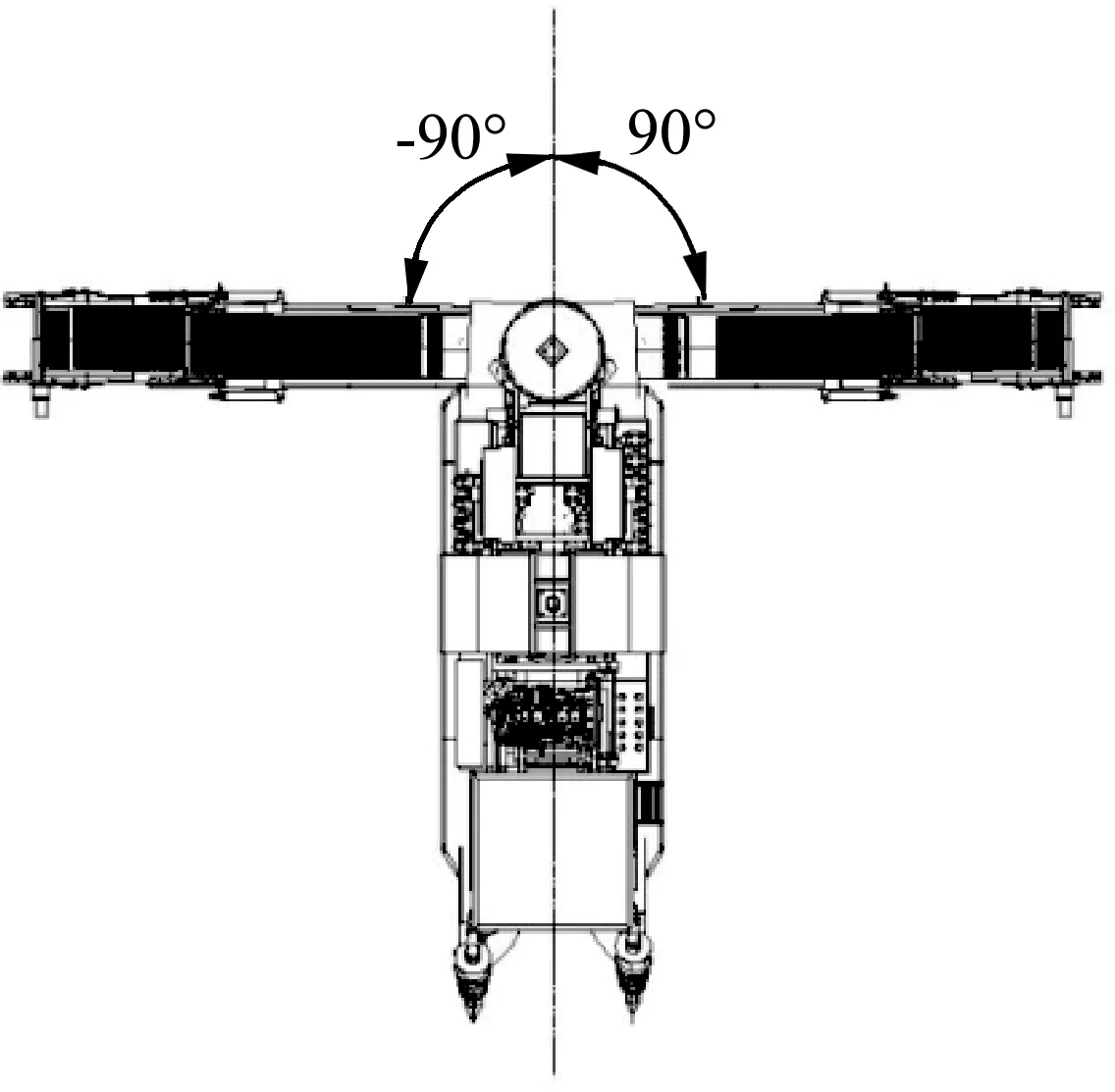
图2 A机输送臂水平旋转俯视图Fig.2 Top view of horizontal rotation of conveyor arm of machine A

2 坡道行驶稳定性分析

收割机在缓坡地和丘陵山地等复杂路面行驶时,坡道行驶稳定性是一项重要技术指标。行驶稳定性是指收割机在正常行驶或者作业时不发生倾翻而能够保持正常工作的能力,通常用极限倾翻角来评定[22]。坡道行驶稳定性包括纵坡和横坡稳定性,其中纵坡分为纵上坡和纵下坡。本文以A机为例作坡道行驶稳定性受力分析。

2.1 纵坡行驶稳定性分析

2.1.1 纵上坡

A机在纵上坡匀速行驶时,如忽略滚动阻力,作用在收割机的力如图3所示。

图3 A机纵上坡受力图Fig.3 Longitudinal upslope stress diagram of machine A

图3中a为前履带轮中心到重心距离,mm;b为后履带轮中心到重心距离,mm;l1为合反力N1到后履带轮中心接地点的距离,mm;h为重心高度,mm;A为前履带轮中心接地点;B为后履带轮中心接地点;α为纵坡坡度,(°);G为重量,kg;L为前后履带轮重心位置长度,mm;F1为A机牵引力,N;O为A机重心;V为行驶方向。

由整机平衡条件得出

bGcosα-hGsinα-N1l1=0

(1)

经简化得

(2)

A机不发生倾翻的条件为l1≥0,即bcosα-hsinα≥0,因此纵上坡极限倾翻角

(3)

2.1.2 纵下坡

A机在纵下坡匀速行驶时,如忽略滚动阻力,作用在收割机的力如图4所示。

图4 A机纵下坡受力图Fig.4 Longitudinal downslope stress diagram of machine A

图4中l2为法向作用力N2到前履带轮中心接地点的距离,mm;F2为A机制动力,N;N2为两履带收割机法向作用力,N。

由整机平衡条件得出

N2l2+Ghsinα-Gacosα=0

(4)

经简化得

(5)

A机不发生倾翻的条件为l2≥0,即acosα-hsinα≥0,因此不倾翻的纵下坡极限倾翻角

(6)

2.1.3 纵坡极限倾翻角分析

由式(3)和式(6)可知,两机纵坡极限倾翻角只与其重心位置有关,与整机重量无关,B机纵坡极限倾翻角计算方法与A机一致。

计算纵坡极限倾翻角时,需要测量重心点O的位置参数,分别以A机的履带前导向轮圆点与B机的前履带轮支架中心点为参考点(图1中A点),以收割机前进方向为X轴,侧向为Y轴,垂向为Z轴。由上述纵坡行驶稳定性分析知,当A机输送臂水平旋转±90°时,纵坡受力分析结果相同,因此本文仅分析A机输送臂水平旋转+90°时对纵坡行驶稳定性的影响。运用SolidWorks三维软件对两收割机进行建模,并对重心位置进行测量。两机的重心位置如表2所示。

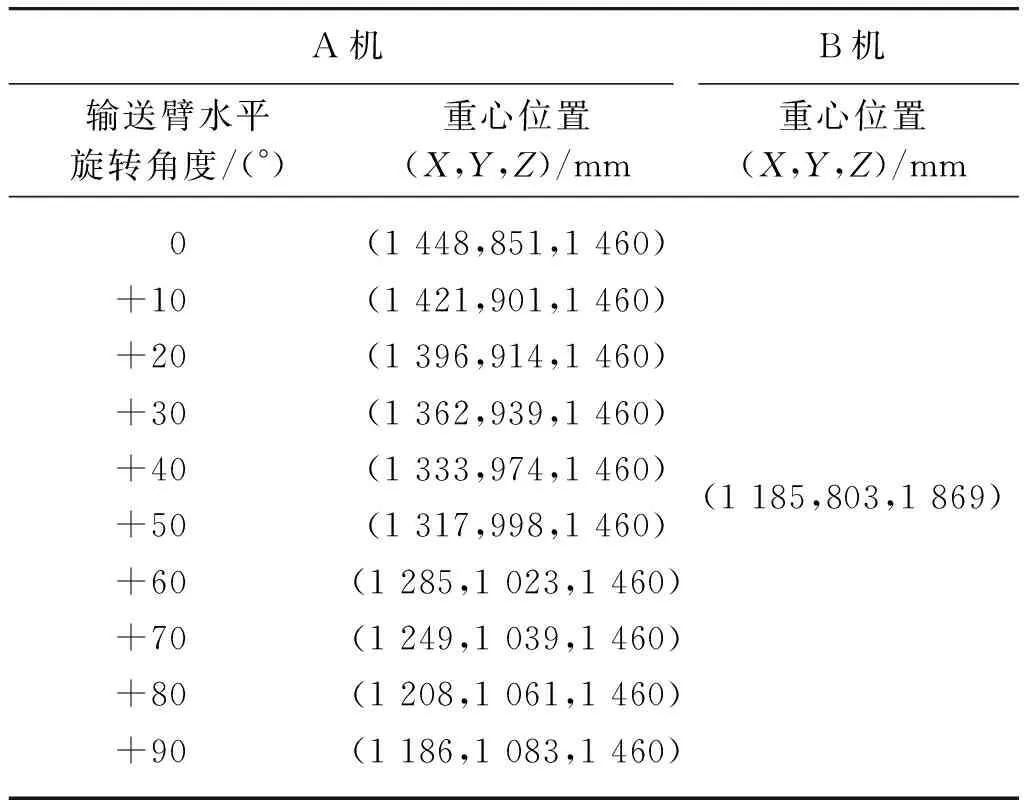
表2 两机重心位置Tab.2 Center of gravity of the two machines

根据两机的基本结构参数和重心位置参数,计算两机纵坡极限倾翻角的理论值,如表3所示。A机输送臂水平旋转角度对纵坡极限倾翻角的影响,如图5所示。

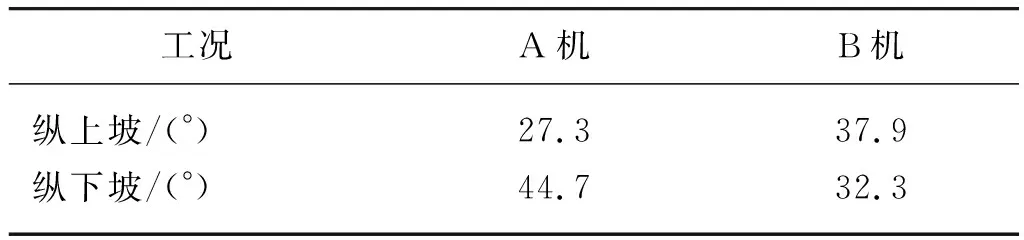
表3 两机纵坡极限倾翻角Tab.3 Limit tilting angle of longitudinal slope of two machines

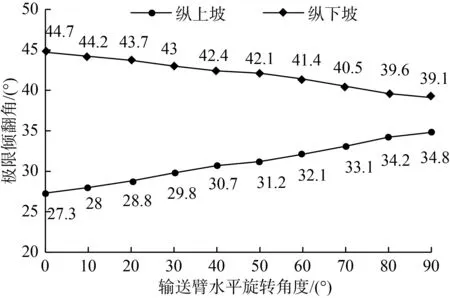
图5 A机输送臂水平旋转角度对纵坡极限倾翻角的影响Fig.5 Influence of horizontal rotation angle of machine A’s elevator on the limit tilting angle of longitudinal slope

如表3所示,B机纵上坡极限侧翻角大于A机,纵下坡极限侧翻值小于A机。由分析可知,B机纵上坡行驶稳定性好于A机,而纵下坡稳定性A机优于B机。是由于B机重心纵向位置比A机靠前(即B机重心X轴数值比A机小),两机重心位置不同,对两机纵坡行驶稳定性造成不同影响。

从图5可知,A机在纵上坡行驶时,输送臂水平旋转角度越大,纵上坡极限倾翻角越大,而在纵下坡行驶时则相反。结合表2可知,由于A机重心位置随输送臂水平旋转角度的变化而改变,因此对纵坡稳定性产生了影响。

2.2 横坡行驶稳定性分析

A机在横坡上行驶时,受力如图6所示。

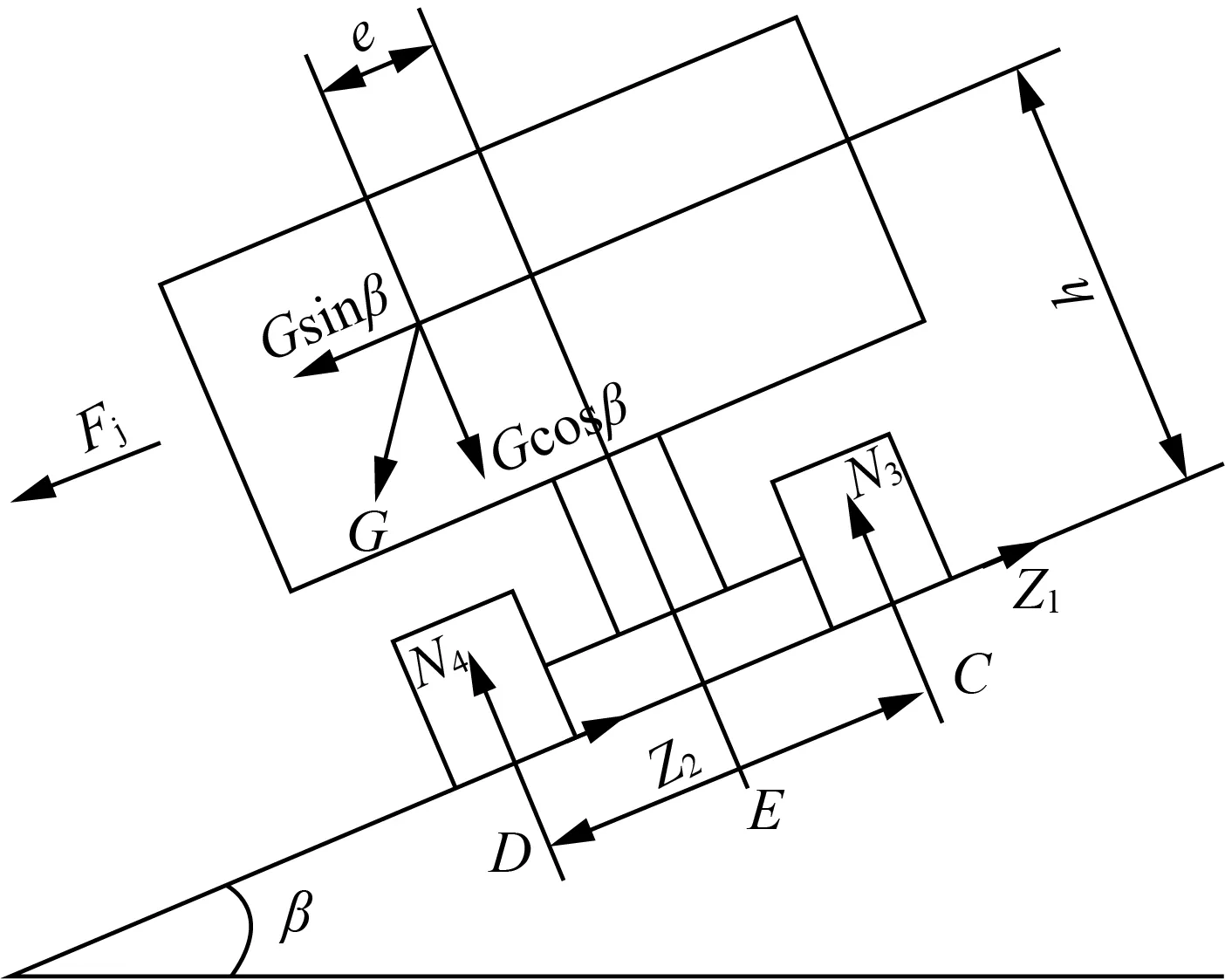
图6 A机横坡受力图Fig.6 Transverse slope stress diagram of machine A

图6中e为重心至收割机纵向中线的距离,mm;C为右侧履带轮中心接地点;D为左侧履带轮中心接地点;E为轮距,mm;Fj为惯性力,N;N3为坡度对右侧履带轮的垂向反力,mm;N4为坡度对左侧履带轮的垂向反力,mm;Z1为坡道对右侧履带轮的侧向反力,N;Z2为坡道对左侧履带轮的侧向反力,N;β为横坡坡度,(°)。

由整机平衡条件可得

N3+N4=Gcosβ

(7)

Z1+Z2=Gsinβ

(8)

(9)

由式(9)可得

(10)

收割机不发生倾翻的条件为N3≥0,即(0.5E-e)cosβ-hsinβ≥0,因此横向极限倾翻角

(11)

运用SolidWorks软件测量A机输送臂水平旋转角度±90°～0°的重心至纵向中线距离e值,可知输送臂水平旋转+90°～0°时比输送臂水平旋转-90°～0°时的重心至纵向中线距离e值大。根据式(11)可知,输送臂水平旋转+90°～0°时比输送臂水平旋转-90°～0°时的横坡极限倾翻角大,即越容易发生横坡行驶倾翻危险,因此需要分析输送臂水平旋转+90°～0°时的横向极限倾翻角。两机重心至纵向中线的距离e值,如表4所示。

表4 两机重心至纵向中线的距离Tab.4 Distance from the center of gravity of the two machines to the longitudinal center line

通过橫坡行驶理论分析,并结合两机基本结构尺寸测量和两机重心至纵向中线距离e值,根据式(11)计算橫坡极限倾翻角值。B机橫坡极限倾翻角为19.3°。A机横坡极限倾翻角受输送臂水平旋转角度的影响,如图7所示。

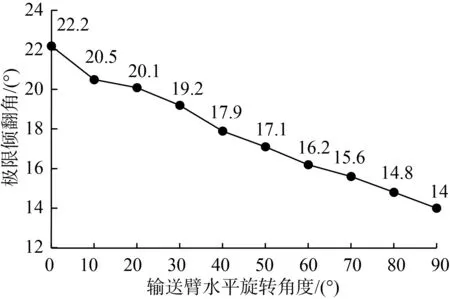
图7 A机输送臂水平旋转角度对橫坡极限倾翻角的影响Fig.7 Influence of horizontal rotation angle of machine A’s elevator on the limit tilting angle of transverse slope

由图7可知,A机输送臂水平旋转角度越大,横坡极限倾翻角越小,即A机在横坡行驶越不稳定。A机输送臂为0°时,橫坡极限倾翻角为22.2°;输送臂为+90° 时,橫坡极限倾翻角为14.0°。A机输送臂为0°的横坡行驶稳定性优于B机,是由于A机重心高度比B机小。

当A机输送臂水平旋转至+30°时横坡极限倾翻角为19.2°,A机小于B机,说明A机输送臂水平旋转角度不超过+30°时,横坡稳定性好于B机。因此A机在横坡行驶时,输送臂尽量以较小的水平旋转角度行驶。

3 坡道行驶稳定性仿真

上述两机坡道行驶稳定性的理论分析,只考虑了两机的基本机构尺寸,未考虑路况影响,因此需引入路面模型,对两机进行坡道行驶动态仿真分析。

3.1 履带收割机三维模型的建立

首先根据两机实际结构尺寸,利用SolidWorks三维软件绘制车体三维模型,并赋予其材料和重量,然后转成t_t格式文件导入到RecurDyn软件中,利用RecurDyn软件中的Track-LM模块绘制两机的履带行走机构。两机三维模型如图8所示,两机履带模型仿真结构如图9所示。

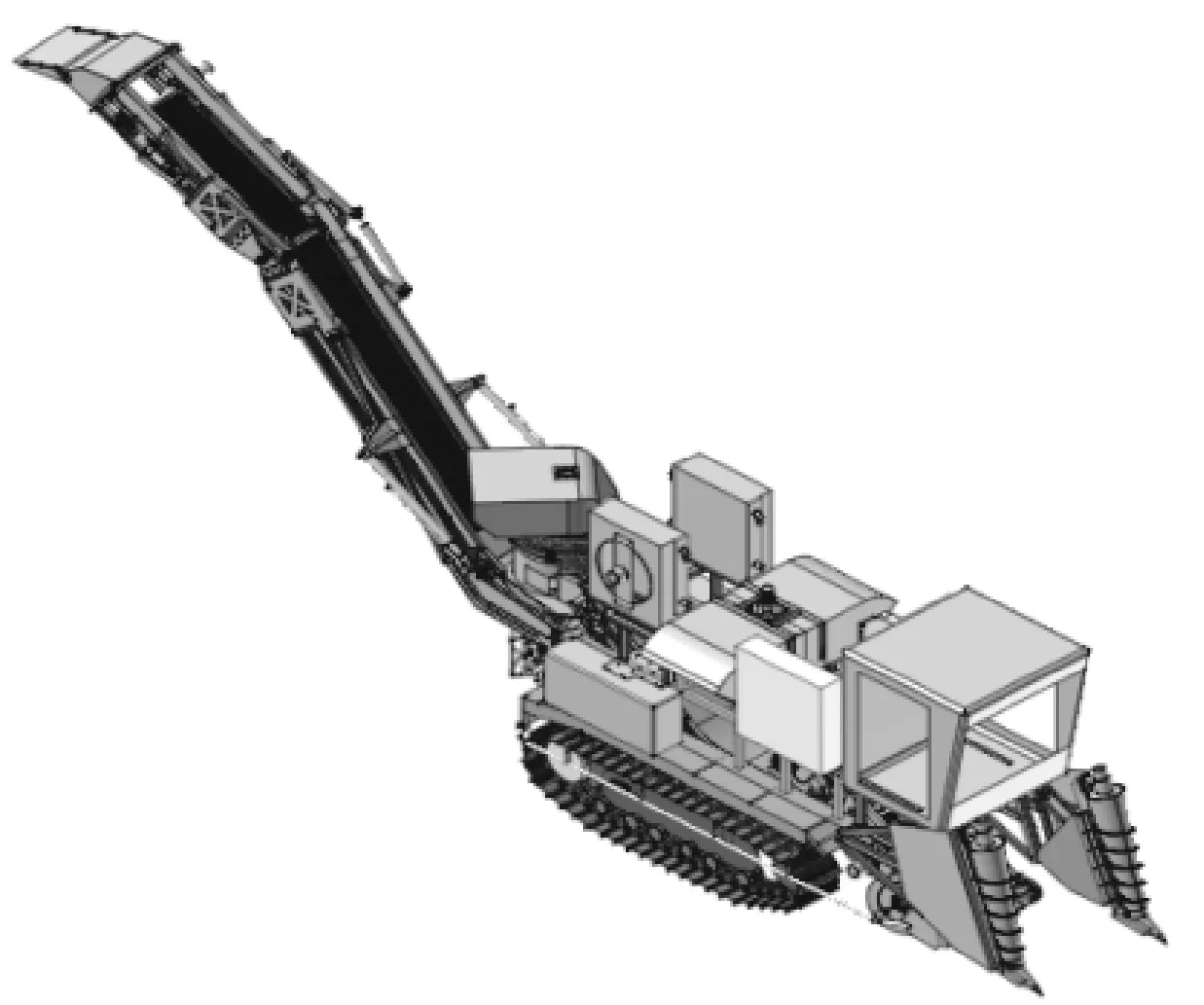
(a) A机三维模型图

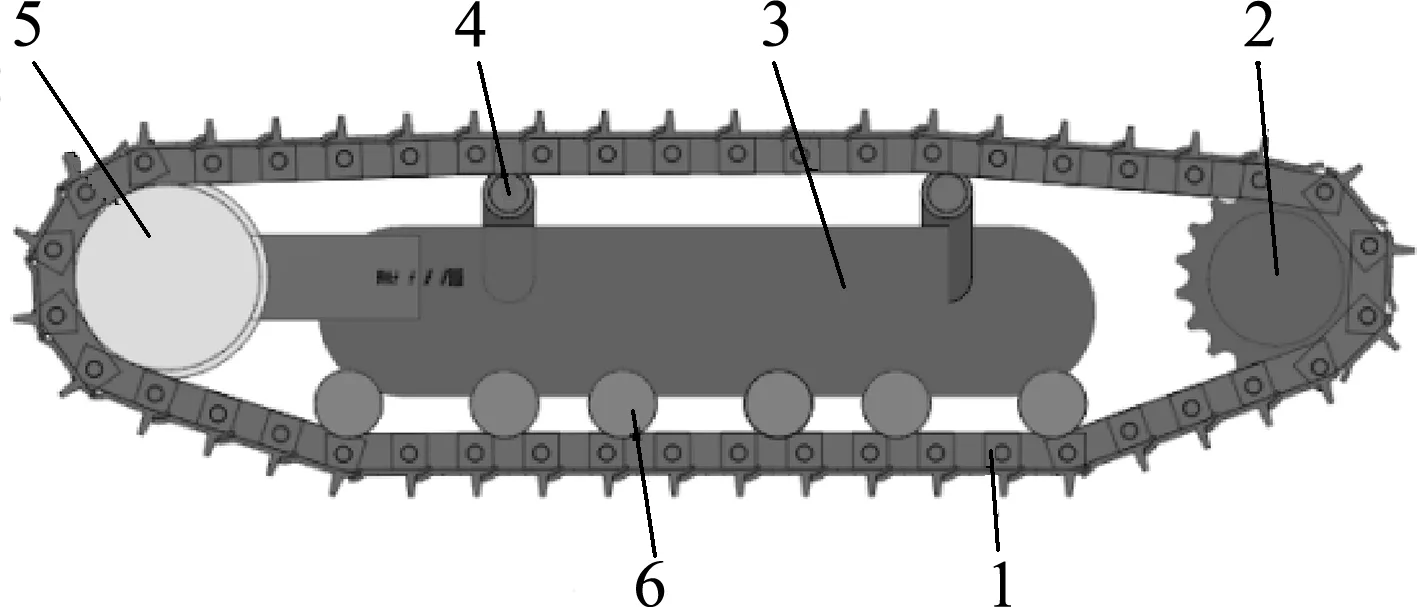
(a) A机履带模型仿真结构图

3.2 施加驱动函数与约束

履带行走机构三维模型构建完成后,还需要对履带行走机构的驱动轮添加驱动函数,对各组件添加驱动副约束,才能够使行走机构产生运动趋势。两机实际作业平均速度为2.5 km/h,对应速度驱动函数为STEP(TIME,0,0D,0,152D)。运动副约束设置如表5所示。

表5 各组件之间的约束Tab.5 Constraints between components

3.3 建立路面模型

我国甘蔗种植区域的特有土壤类型为红壤土[21],其土壤黏聚力值为24 kPa。本文参考红壤土路面模型的黏聚力数值,选取路面模型为土壤黏聚力值13.79 kPa的壤土(Sandy loam)路面模型,其路面特征参数如表6所示。

表6 壤土路面模型特征参数Tab.6 Characteristic parameters of loam pavement model

3.4 坡道行驶性能仿真

根据两机坡道行驶性能分析,得出两机纵坡与横坡极限倾翻角理论值。参考两机极限倾翻角理论值,A、B两机分别以24°、35°为起点坡度进行纵上坡行驶仿真;以36°、27°为起点坡度进行纵下坡行驶仿真;以12°、16°为起点坡度进行橫坡行驶仿真。两机行驶仿真的坡度以每1°进行递增,至两机行驶发生倾翻即为两机动态极限倾翻角。两机在长度20 m坡面以2.5 km/h 匀速行驶,得出两机在壤土路面下行驶的重心高度变化规律。

3.4.1 纵上坡仿真

两机纵上坡行驶仿真结果如图10所示,当A机输送臂水平旋转0°时,能够在24°坡面稳定行驶,在25°坡面行驶至19 s时发生倾翻。当A机输送臂水平旋转+90°时,能够在31°坡面稳定行驶,在32°坡面行驶至22 s时发生倾翻。即A机输送臂水平旋转0°和+90° 的纵上坡极限倾翻角分别为24°和31°。输送臂水平旋转+90°比0°的纵上坡极限倾翻角大,且发生倾翻的时间更短。B机能够在35°坡面稳定行驶,在36°坡面行驶至24 s时发生倾翻,即B机纵上坡极限倾翻角为35°。由此可知,B机纵上坡极限倾翻角比A机大,且发生倾翻的时间更短。综上分析,在不考虑其他外界激励情况下,纵上坡行驶稳定性,B机比A机好,A机输送臂水平旋转+90°比0°好。

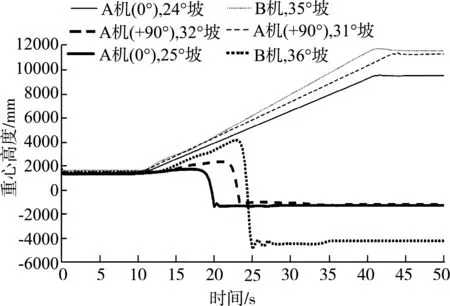
图10 两机纵上坡行驶的重心高度关系曲线Fig.10 Relation curve of gravity center height of the two machines driving longitudinally upslope

3.4.2 纵下坡仿真

两机纵下坡行驶仿真结果如图11所示,当A机输送臂水平旋转0°时,能够在36°坡面稳定行驶,在37°坡面行驶至14 s时发生倾翻;当A机输送臂水平旋转+90° 时,能够在32°坡面稳定行驶,在33°坡面行驶至14 s时发生倾翻;即A机输送臂水平旋转0°和+90° 的纵下坡极限倾翻角分别为36°和32°。输送臂水平旋转0°比+90°的纵下坡极限倾翻角大。B机能够在27°坡面稳定行驶,在28°坡面行驶至14s时发生倾翻,即B机纵下坡极限倾翻角为27°。由此可知,B机纵下坡极限倾翻角比A机小。综上分析,在不考虑其他外界激励情况下,纵下坡行驶稳定性,A机比B机好,A机输送臂水平旋转0°比90°好。

图11 两机纵下坡行驶的重心高度关系曲线Fig.11 Relation curve of gravity center height of the two machines driving longitudinally downslope

3.4.3 橫坡仿真

两机横坡行驶仿真结果如图12所示,A机输送臂水平旋转-90°、0°、+90°时,能够分别在21°、18°、12°坡面稳定行驶。当坡面分别增加至22°、19°、13°时,重心高度值迅速减小,发生倾翻,即A机输送臂水平旋转-90°、0°、+90°的横坡极限倾翻角分别为21°、18°、12°。综合A机横坡受力分析(图6)和上述A机横坡仿真结果,可得出输送臂水平旋转角度越靠近下坡面方向,越容易发生倾翻。是由于输送臂水平旋转角度越靠近下坡面,整机重心位置也偏向下坡面。说明横坡行驶时,为提高行驶稳定性,A机输送臂水平旋转角度应与坡面倾斜角度相反。B机能够在16°坡面稳定行驶,在17°坡面行驶至2 s时发生倾翻,即B机横坡极限倾翻角为16°。可得出A机输送臂水平旋转角为0°和-90°时极限侧翻角大于B机。A机输送臂水平旋转角度为+90°时,极限倾翻角小于B机。

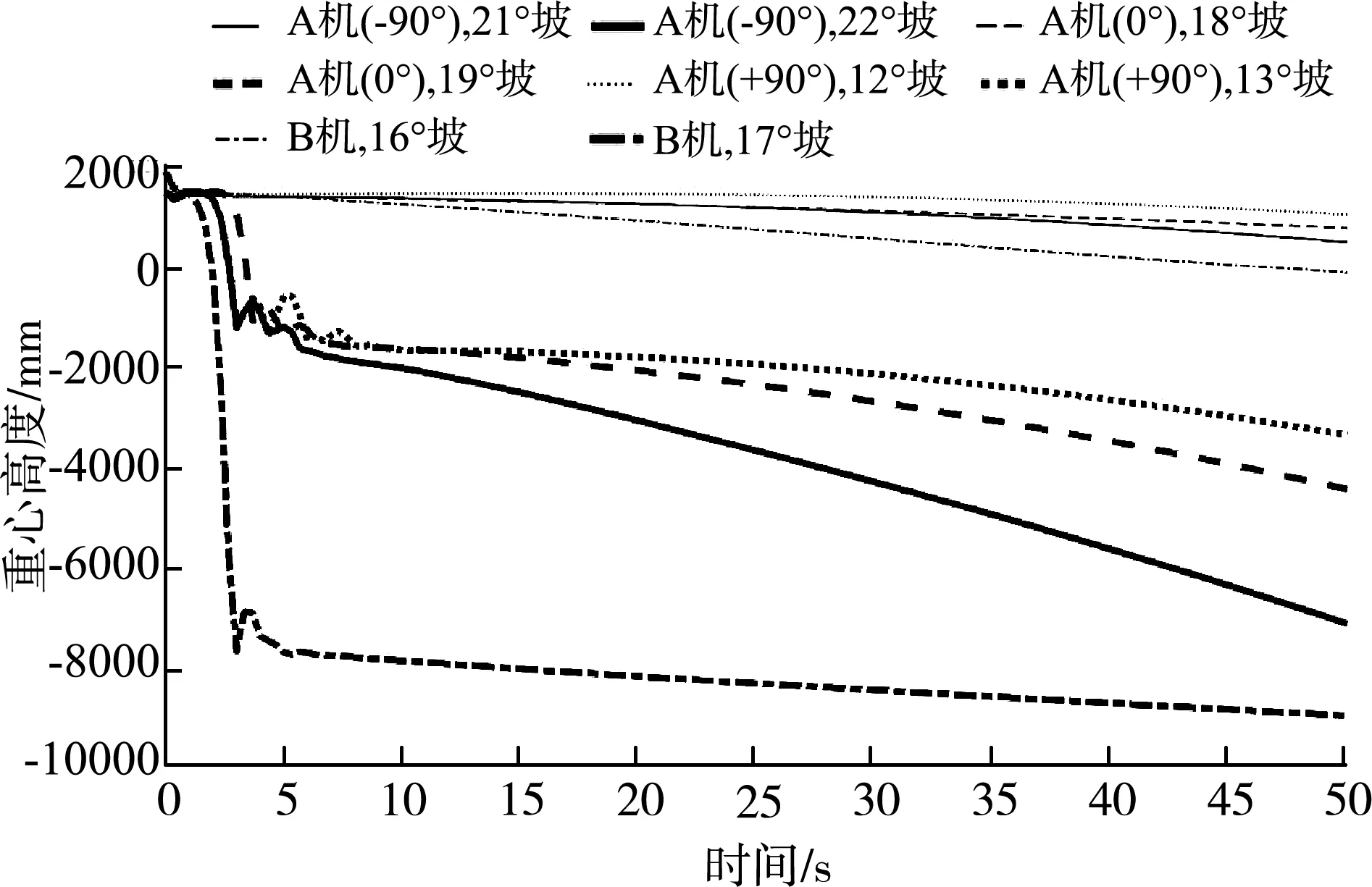
图12 两机橫坡行驶的重心高度关系曲线Fig.12 Relation curve of gravity center height of the two machines driving on transverse slope

3.5 坡道行驶稳定性仿真结果分析

两机纵上坡行驶极限倾翻角理论值与仿真值如图13所示。由图13可知,两机极限倾翻角数值由大到小依次为：B机、A机输送臂水平旋转+90°、A机输送臂水平旋转0°。A机输送臂水平旋转0°、+90°和B机的极限倾翻角理论值与仿真值相对误差分别为：12.09%、10.92%、7.71%,进一步说明了仿真能够有效反应两机的纵上坡行驶稳定性,且B机纵上坡行驶稳定性比A机好。是由于B机长度比A机短,没有可旋转式输送臂,重心纵向位置比A机靠前,因此纵上坡行驶时B机稳定性比A机好。

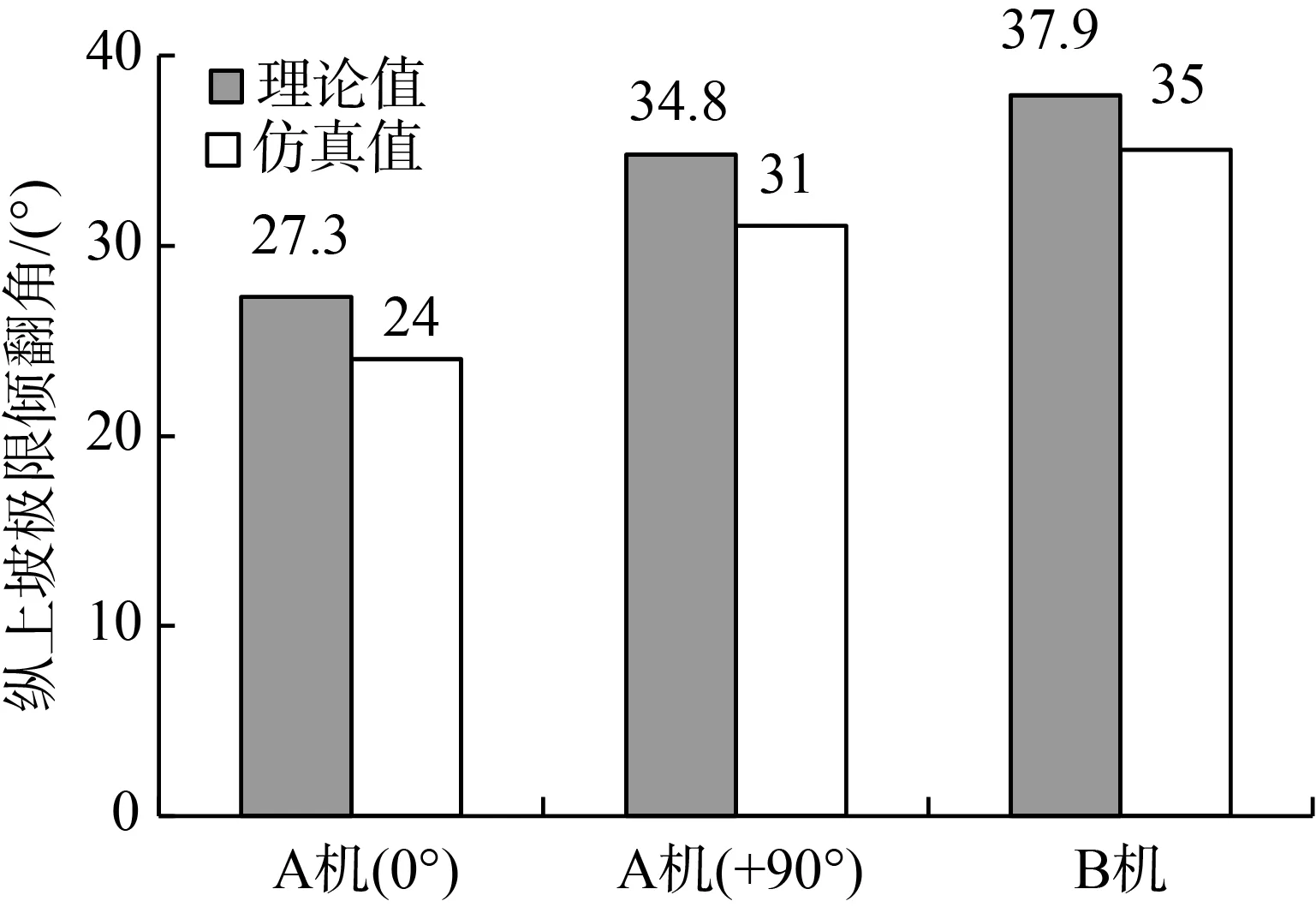
图13 两机纵上坡行驶极限倾翻角理论与仿真值Fig.13 Theory and simulation value of limit tilting angle of two machines driving on longitudinal upslope

两机纵下坡行驶极限倾翻角理论值与仿真值如图14所示。由图14可知,两机极限倾翻角数值由大到小依次为：A机输送臂水平旋转0°、A机输送臂水平旋转+90°、B机。A机输送臂水平旋转0°、+90°和B机的极限倾翻角理论值与仿真值相对误差分别为：19.46%、18.16%、16.41%,进一步说明了仿真能够有效反应两机的纵下坡行驶稳定性,且A机纵下坡行驶稳定性比B机好。是由于A机质量比B机小,并且A机有输送臂,重心位置比B机靠后,纵下坡行驶时,输送臂重量可以抑制A机行驶动能,防止发生侧翻危险。因此纵下坡行驶时A机稳定性比B机好。

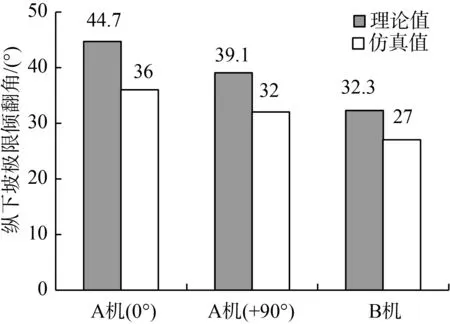
图14 两机纵下坡行驶极限倾翻角理论与仿真值Fig.14 Theory and simulation value of limit tilting angle of two machines driving on longitudinal downslope

两机橫坡行驶极限倾翻角理论值与仿真值如图15所示。由图15可知,两机极限倾翻角数值由大到小依次为：A机输送臂水平旋转-90°、A机输送臂水平旋转0°、B机、A机输送臂水平旋转+90°。A机输送臂水平旋转0°、+90°、-90°和B机的极限倾翻角理论值与仿真值相对误差分别为：18.91%、14.28%、12.86%、17.10%。仿真结果表明：A机输送臂水平旋转角为-90°～0°时,横坡行驶稳定性比B机好;A机输送臂水平旋转角为+90°时,横坡行驶稳定性比B机差。由于A机输送臂水平旋转角度为-90°～0°时,重心至纵向中线的距离e值比B机小,同时,A机重心高度比B机小。因此当A机输送臂水平旋转角度为-90°～0°时,横坡行驶稳定性比B机好,A机输送臂水平旋转角度为+90°～0°时则相反。

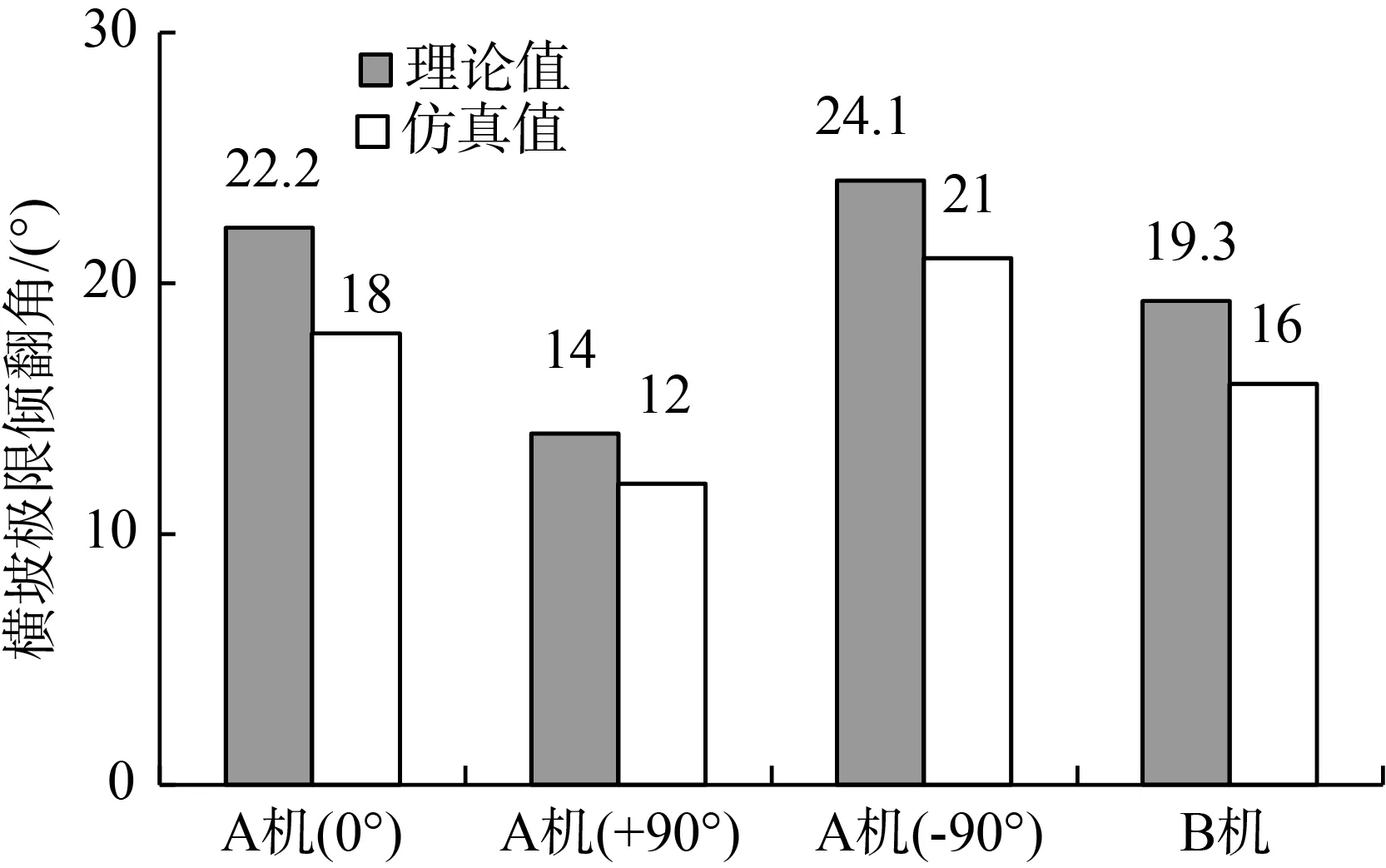
图15 两机橫坡行驶极限倾翻角理论与仿真值Fig.15 Theory and simulation value of limit tilting angle of two machines driving on transverse slope

综上分析,可得出两机纵坡和横坡的极限倾翻角理论值与仿真值较为接近。理论值都比仿真值大,是由于仿真时设定了壤土的路面参数,更真实的反映出两机坡道行驶性能。理论值和仿真值相对误差最大为18.91%,根据相关经验和参考文献[22-23]可知相对误差在合理范围内。说明仿真能够有效反映两机的坡道行驶稳定性,可为甘蔗收割机底盘设计提供参考。