螺旋管内局部二次流强度计算及演变规律
2023-07-10吴金星李松歌肖嘉邦马宇翔
吴金星, 徐 耀, 李松歌, 肖嘉邦, 马宇翔
(郑州大学 机械与动力工程学院,河南 郑州 450001)
二次流是指在一定的主流速度下和一定的几何边界条件下作曲线运动的黏性流体所产生的一种有规律的伴随运动[1]。螺旋管中的流体由于受到离心力、科氏力、浮力等作用会产生的一对呈反向涡旋的二次流——迪恩涡[2]。迪恩涡有着独特的流场结构:一方面迪恩涡可在避免湍流的情况下加强管内流体的扰动,使管内流体的横向对流作用显著增强[3-6];另一方面在迪恩涡作用下,靠近管壁的流体对管壁的剪切作用可以减薄边界层厚度、防止管壁结垢[7]。因此,螺旋管被广泛运用于石油、化工、制冷、空分等领域。
威廉·雷金纳德·迪恩在小曲率条件下得到了圆形截面弯管内流动的摄动解,并且提出了判断管道内二次流的强度的准则数迪恩数(De)[2]。迪恩数代表的是离心力与黏性力的比值,同时也衡量着二次流的强度[8]。
螺旋管作为强化传热的手段使用已久,以往对螺旋管的优化和二次开发通常是通过对比整体传热和流动特点来进行的。也有学者用了多种方法衡量弯管内的二次流强度,大体上可以分为4种。第1种是通过观察流线图来判定局部二次流强度,这种方法只能做定性的判断,并且带有主观性。第2种是通过计算速度在垂直于主流方向的截面上的分量大小来判断[9]。但是,在很多情况下垂直于主流方向的横向运动并非由二次流引起,如在直管中的湍流流体也有垂直于主流方向的横向运动,所以单纯地计量垂直于主流方向的横向运动速度不足以说明二次流的强度。第3种是通过计算各节点的流体速度与主流速度的比值来阐述螺旋管内二次流特性[5,10]。但螺旋管壁面附近流体速度受边界层的影响,与主流速度的比值总是趋于0,因此该方法无法对边界层流体的流动变化特性进行表达,也无法分析螺旋管结构对边界层处流体的影响。第4种是通过计算局部涡量或纵向涡及所衍生出来的无量纲数来衡量二次流的强度[11]。但是弯管近壁面处速度变化剧烈,存在着不是因二次流而产生的涡量,且通常近壁面处的涡量非常大,这给观察和计量主流区的二次流强度带来了干扰。虽然衡量局部二次流强度的方法众多,但是这些方法都存在着局限性,这就导致了工程人员难以精准地调控二次流强度。
本文提出了一个描述局部二次流强度的无量纲指标H,验证各种条件下的H的体积平均值与迪恩数是否为线性关系,并探究了螺旋管内流体的二次流演变规律,为螺旋管内二次流的调控及强化管的开发提供了参考指标。
1 理论分析
图1为螺旋管截面流线图,在靠近上壁面ab和下壁面ef的流体受黏滞力作用速度相对较小,而中心处的流速较大。因流速大的微粒离心惯性大,所以沿着中心线dc区域流线的压强增量将大于ab和ef线的压强增量。因此c处的压强将大于a和e处的压强,流体自c处流向a和e处,而d处的流体也将靠离心惯性不断地向c处流去[12]。这样,d处的压强将小于b处和f处的压强,二次流变在径向平面内发生,其旋转方向如图1所示。这两个旋转运动与主流相结合,便产生了双螺旋流动。
综合截面上的速度分量的特性与主流速度对二次流强度的影响,本文提出使用螺旋强度he来计算局部二次流强度,其计算方法如下:
(1)

(2)
式中:Ω为局部涡量;U为速度矢量;涡量与速度矢量的点积,代表了其与速度的协同程度,取绝对值是因为无论二次流在截面上的流动是顺时针还是逆时针,对传热的影响是一样的。
由于二次流强度受速度、密度、特征长度、黏度影响,所以,he为速度、密度、特征长度、黏度的函数,表示为
he=f(U,ρ,d,μ)。
(3)
式中:5个物理量的量纲均由3个基本量纲(时间量纲、长度量纲、质量量纲)组成,故可以组成2个无量纲数。选定特征长度、密度、黏度为基本物理量。在此只分析包含he的无量纲数H。设:
H=he·daρbμc。
(4)
由量纲和谐原理得
dimH=M0.5+a-3b-cT-1-cLb+c。
(5)
即a=1.5,b=1,c=-1。
所以,代表着局部二次流强度的无量纲数H表示为
(6)
为描述截面上的平均二次流强度,使用截面局部二次流强度H的面积平均值Ha,其计算式为
(7)
式中:i代表第i个网格节点;si为节点在截面上的面积。
由局部的二次流强度的无量纲数,通过对流域的体积积分并除以总体积,即可得到描述全场的二次流强度,即H的体积平均值:
(8)
为验证本文所提出的局部二次流强度计算方法的准确性,以螺旋管内流体为对象,验证不同参数下的Hm与De的相关性。两者的相关性系数计算式为
(9)

2 数值模拟验证
2.1 几何模型
螺旋管的几何参数如图2所示。d为螺旋管的内径,D为螺旋管的缠绕直径,P为螺距。L为螺旋管长度,在本文中所有模型的螺旋管长度保持一致。
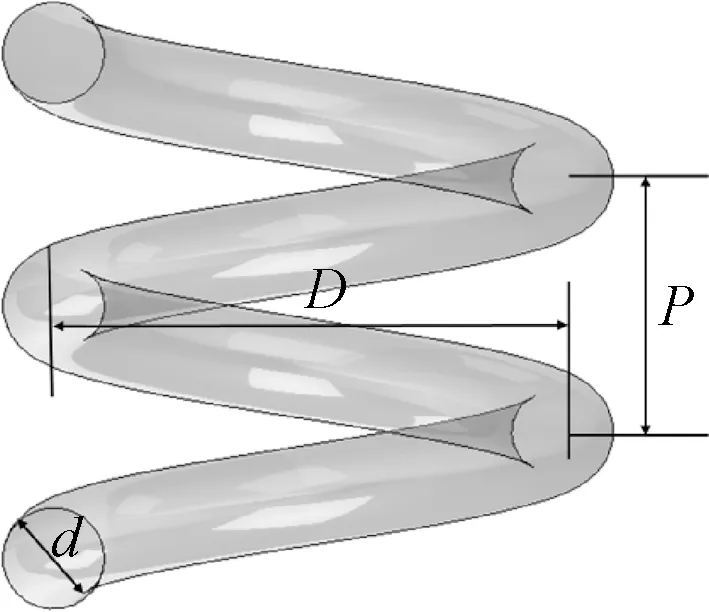
图2 螺旋管几何模型Figure 2 Geometric model of helical tube
定义螺旋曲率[4]为
δ=d/D。
(10)
无量纲螺距为
λ=P/(πD)。
(11)
缠绕圈数为
(12)
雷诺数计算式为
(13)
临界雷诺数[13]为
(14)
迪恩数定义[14]为
(15)
式中:Dc为曲率的平均直径,计算式[7,15]为
(16)
于是De可以写成
(17)
2.2 边界条件
入口为速度入口,出口为压力出口,壁面为静止、无滑移,恒壁温,不计壁厚。
2.3 求解方法
数值模拟使用的求解器是FLUENT 2019。模型为层流稳态模型。速度压力耦合计算采用SIMPLE算法。同时设置收敛残差标准为1×10-6,对出入口处质量流量以及压力差进行监控,最终确定模拟达到收敛。
2.4 网格无关性验证
计算域的网格划分方式采用六面体结构化网格,并对近壁面的网格进行了局部加密。网格无关性验证选取6套网格尺寸不同的方案,以网格最小的方案为标准,计算其他5套方案的努塞尔数与压降的相对误差,结果如图3所示。综合考虑准确性与效率,选取第3套网格划分方案(网格数为2 190 617)。
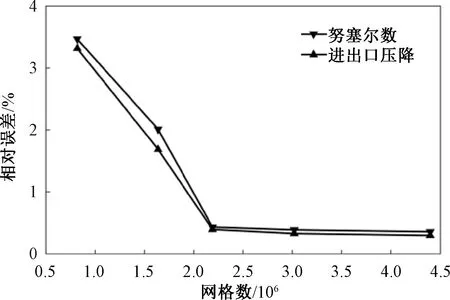
图3 网格无关性验证Figure 3 Grid independence verification
2.5 数值模拟方法验证
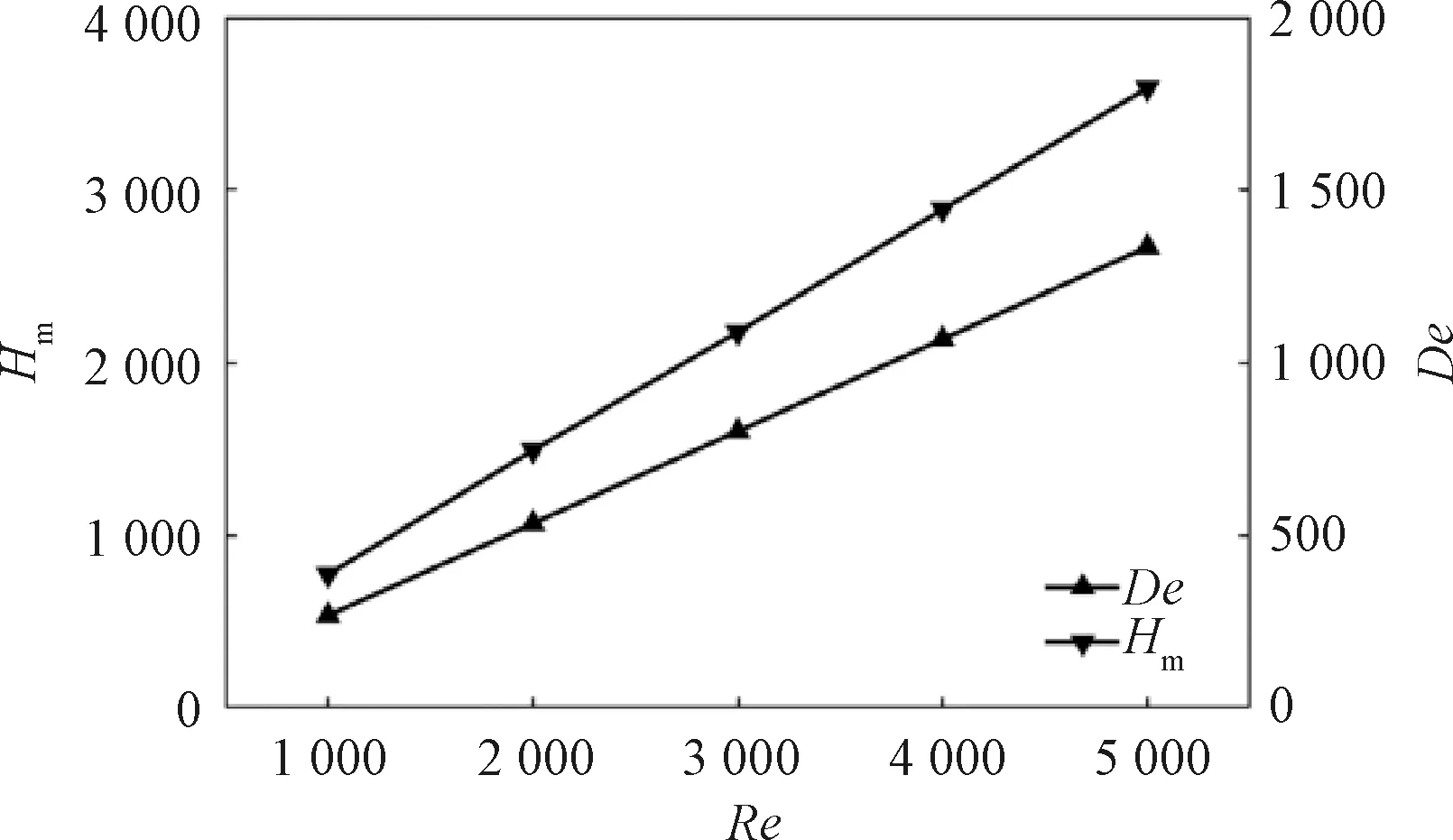
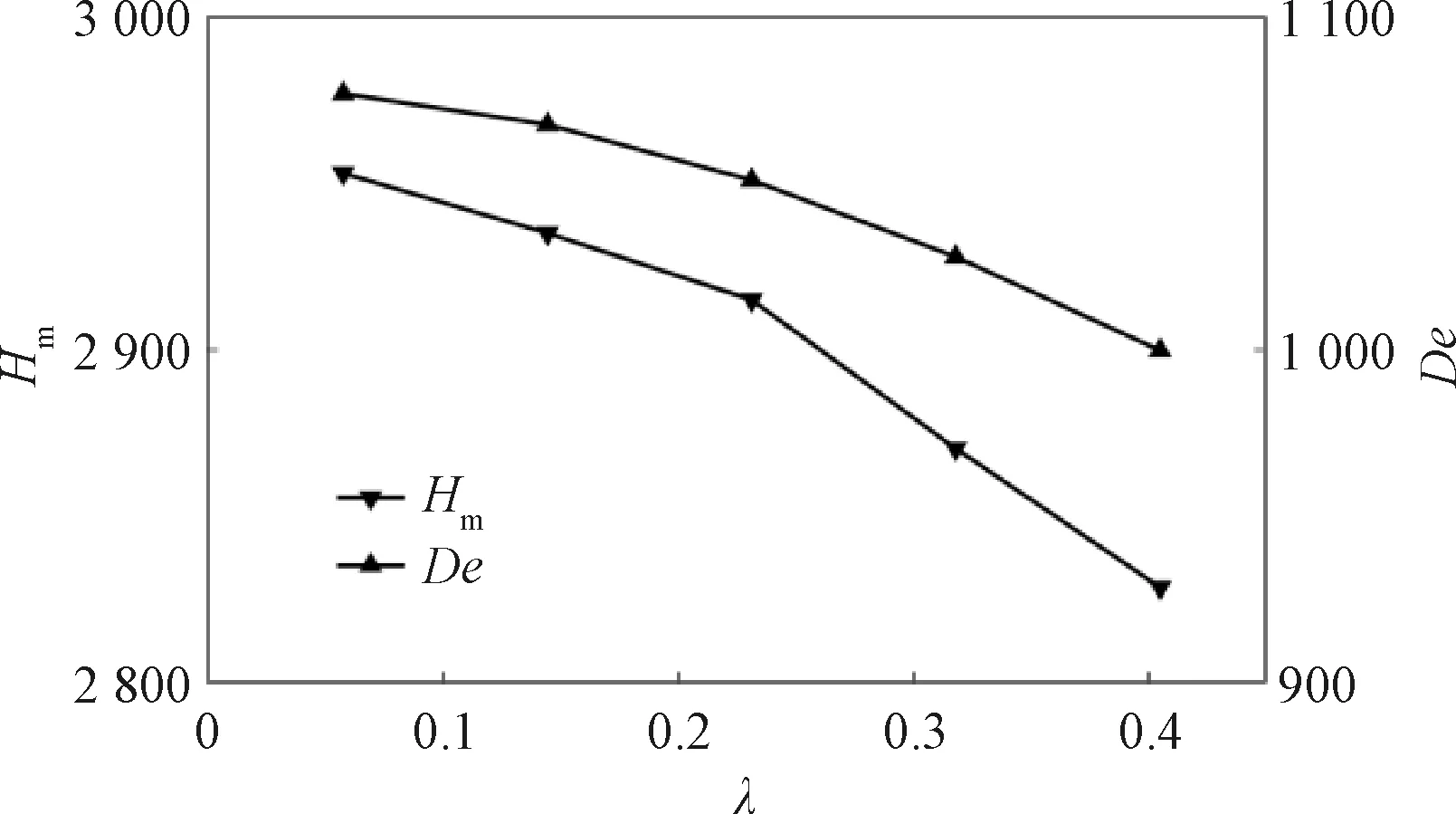
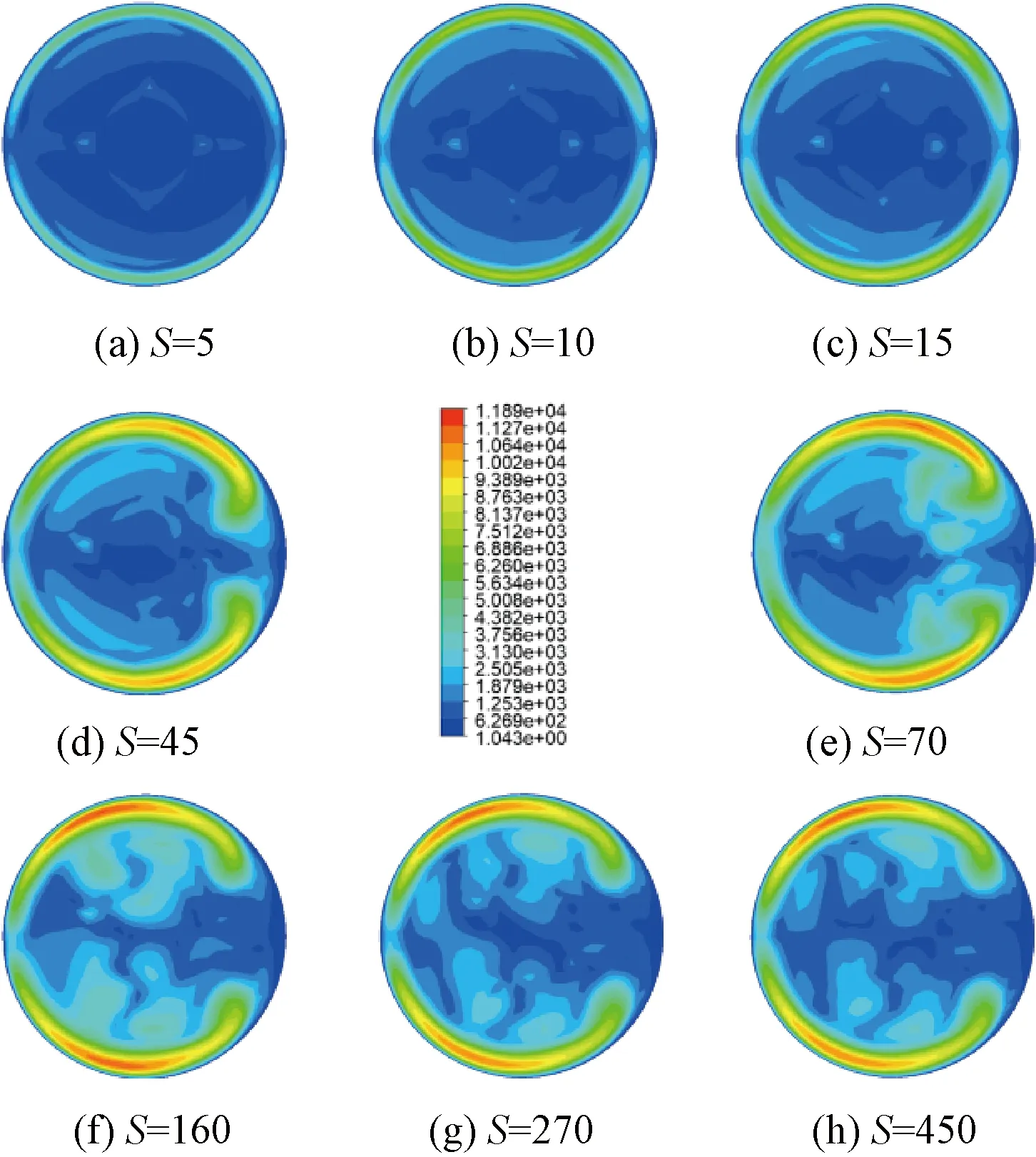
为验证数值模拟方案的可靠性,以水为介质,在d为8 mm、D为110 mm、P为50 mm,雷诺数为1 000~5 000的工况下将模拟值与文献[16]中的公式(见式(18),适用于500 图4 数值模拟方案可行性验证Figure 4 Feasibility verification of numerical simulation scheme Nu=0.152De0.431Pr1.06λ-0.277。 (18) 采用d为8 mm、D为110 mm、P为50 mm的螺旋管结构,验证不同雷诺数下De与Hm的相关性,结果如图5所示。随着雷诺数的增大,流体的主流方向速度增大,受到的离心力也增大,从而在径向上的分速度增大,导致了二次流强度增加。在不同的雷诺数下,De与Hm都随Re的增大而增大。进一步分析De与Hm的数值特征,两者几乎成正比关系,Hm/De在2.71~2.80。说明在不同雷诺数下,H的体积平均值能够很好地描述整体二次流的强度,用H作为局部二次流强度指标是合理的。 图5 不同雷诺数下Hm与De关系图Figure 5 Relationship diagram of Hm and De at different Reynolds numbers 若螺距无穷大,此时螺旋管近似为直管,二次流不会发生,De为0。但是在实际工程应用中,螺距的变化范围有限,对二次流的影响相对很小。为验证不同螺距下De与Hm的关系,选取d为8 mm、D为110 mm、P为20~140 mm(无量纲螺距λ为0.057 9~0.405 1)的螺旋管结构,雷诺数恒定为4 000,结果如图6所示。因螺距的增加导致了螺旋管整体的弯曲程度减小,流体受到的离心力减小,De与Hm都随无量纲螺距的减小而减小,但是其减少的幅度很小。Hm/De在2.74~2.82之间。 图6 不同螺距下Hm与De关系图Figure 6 Relationship diagram of Hm and De at different pitch 为验证不同曲率下De与Hm的关系,选取d为8~12 mm(曲率为0.072 7~0.109 1)、D为110 mm、P为50 mm的螺旋管结构,雷诺数恒定为4 000,结果如图7所示,De与Hm都随曲率的增加而增加,Hm/De在2.68~2.77。 图7 不同曲率下Hm与De关系图Figure 7 Relationship diagram of Hm and De at different curvature 若局部二次流强度指标H能够精准描述局部二次流强度,则依据式(9),理论上H的体积平均值Hm与De的相关系数应为1。但是由于舍入误差的存在,所有样本点的Hm与De的相关性系数r为0.994 9,十分接近于1,且Hm/De都在2.75左右,说明Hm和De存在着较好的正比关系,同时也说明H作为螺旋管内局部二次强度指标是可行的。 以水为工质,选取d为8 mm、D为110 mm、P为50 mm、雷诺数恒定为4 000的螺旋管结构为研究对象。图8展示的是螺旋管中各个截面上的Hm,其中S表示的是截面中心沿螺旋中心线距入口的沿程距离。从图8可以看出,流体依据二次流的强度变化趋势,其流动状态可以分为3个阶段:发展段(入口~35 mm)、过渡段(35~200 mm)、稳定段(200 mm~出口)。在发展段,流体从入口进入螺旋管后,在离心力的作用下迅速发展出二次流,二次流强度迅速增大,并在路程S=35 mm时达到极大值。然后流体进入了过渡段,二次流强度在路程S=160 mm处达到最大值,之后二次流强度略有下降。在稳定段,流体在截面上的平均二次流强度在2 850上下呈小幅度规律性波动。 图8 截面面积平均二次流强度与沿程距离的关系Figure 8 Relationship between the average secondary flow intensity and the distance along the cross section area 图9所示为各个截面上的局部二次流强度云图。二次流强度沿着水平线呈对称分布,二次流强度最大区域分布在上下壁面附近,管道中心区域二次流强度相对很小,并且局部二次流强度最大值在发展阶段和过渡阶段逐渐从内侧向外侧转移(各云图的右侧为内侧,左侧为外侧)。 图9 各截面二次流强度云图Figure 9 Intensity diagram of secondary flow 在不同的几何参数或者工况下,螺旋管中的二次流强度和演变规律是不同的。同一根螺旋管在不同雷诺数下,流道各截面上的H的面积平均值分布如图10所示。随雷诺数的增大,螺旋管中的二次流在发展段增大得更快。不同雷诺数下,螺旋管中的流体都经历3个阶段,且3个阶段都发生相同的位置,说明雷诺数只影响二次流的强度,不影响二次流的演变规律。 图10 不同雷诺数下二次流演变规律曲线图Figure 10 Secondary flow development curve at different Reynolds number 图11所示为不同曲率下螺旋管中流体的面积平均二次流强度随沿程距离的变化图。各管中的流体都经历3个阶段,但是强度和3个阶段发生的位置都不同。具体来说,随着曲率的增大,二次流的强度会略微增大,并且到达稳定阶段所需的路程更长。 图11 不同曲率下二次流演变规律曲线图Figure 11 Curve of secondary flow development at different curvature 图12所示为不同螺距的螺旋管中流体的面积平均二次流强度随沿程距离的变化图。5条曲线基本重合,说明螺距对二次流的强度和演变规律影响非常小,随螺距的增大,二次流强度略微减小,3个二次流阶段发生的位置基本一致。 图12 不同螺距下二次流发展规律曲线图Figure 12 Curve of secondary flow development at different pitch (1)无量纲螺旋强度H的体积平均值与迪恩数De相关系数约为1,H/De在2.75左右,H能够准确地描述螺旋管内的局部二次流强度。 (2)螺旋管内流体从垂直于入口流入到流出,依据二次流的强度可以划分为3个阶段,分别为发展段、过渡段和稳定段。二次流在发展段迅速增强,在过渡段出现最大值,在稳定段呈周期性波动。 (3)雷诺数的增大会显著增大二次流强度,但是不影响二次流3个阶段的出现位置。曲率的增大会略微增大二次流的强度,且延长二次流达到稳定阶段的路程。螺距对二次流的强度和发展规律影响非常小。
3 结果与讨论
3.1 不同参数下局部二次流强度计算方法验证

3.2 二次流演变规律

3.3 不同参数对二次流演变规律的影响



4 结论
