一种基于被动声呐宽带空间谱的自动检测算法

2023-07-10柳嵩姚直象陆代强袁骏

兵工学报 2023年6期

柳嵩,姚直象,陆代强,袁骏

(海军工程大学电子工程学院,湖北武汉 430000)

0 引言

受海洋环境噪声波动起伏和多目标相互干扰的影响,被动探测的宽带空间谱中,背景高度在空时二维均存在大幅度波动,尤其强弱目标共存时弱目标不易凸显[1],常用的固定门限检测无法适应这样的复杂环境,主要体现在：1)门限固定性使该算法无法适应波动背景,易产生高虚警;2)强弱目标共存时,为保证弱目标检测概率需降低检测门限,这易检出强目标旁瓣;3)检测门限需依靠一定的先验信息进行人工选取;4)检出的目标在方位历程上跨越多个波束,不能给出目标的精确角度。上述问题限制了目标检测效率,战场环境的复杂多变也对实时检测与自动检测提出更迫切的需求。

针对被动声呐目标检测的相关问题,国内外学者提出诸多检测算法,常见算法主要有：时域检测主要有基于信号相关性检测、波束域能量检测及子带峰值能量检测[2-7];频域检测主要包括信号功率谱、倒谱和高阶统计量的检测算法[8-12];时频分析算法主要包括利用短时傅里叶变换、小波变换等通过信号的时频特性进行的窄带线谱成分的检测[13-14]。上述算法均从提高信噪比的角度入手来提高检测性能,对波束旁瓣漏入的信号没有抑制能力,大多频域检测手段和时频分析主要针对窄带线谱,对宽带目标效果不佳。上述方法均需手动设置门限,未解决门限自适应的问题,近年来出现了基于动态规划、霍夫变换等批处理检测跟踪一体化的被动宽带目标探测方法避免了诸多宽带检测难题[15-17],但收敛速度慢、耗费计算资源多、实时性差,难以工程应用。在主动声呐目标检测领域,为降低背景波动造成的固定门限检测检测性能不佳问题,诸多学者提出了门限自适应选取的方案,诞生了诸如单元平均恒虚警检测、单元平均选小检测、单元平均选大检测、排序统计检测等方法针对声呐图像存在的背景波动、混响和强干扰问题取得较好效果[18]。在被动宽带目标检测领域,鲜有人研究检测门限自适应选取,且大都基于时域或频域信号层面进行检测,对避免检出旁瓣问题较为不利。由于波束有一定的宽度,单个目标在宽带方位历程中有一定宽度,再加上背景起伏,声呐操作员在显控台上选择波束精确测向时,往往因引导波束选取偏差使测向精度变差。

为解决上述问题,实现目标自动检测,提供准确可靠的实时检测结果,本文从宽带波束域空间谱入手,将排序截断平均(OTA)算法[1,19]和局部峰值检测结合,设计了波束域空时自适应检测(BSTAD)算法,并与波束内插算法结合,实现了检测门限自动选取和自动方位估计。该算法可有效适应噪声功率的起伏,且在对弱目标有相同检测概率的前提下对强目标旁瓣有明显压制效果,此外该算法为波束内插提供了精确的引导波束,避免了波束选取偏差。算法基于宽带空间谱即可实现检测与方位估计,所需数据量小、计算复杂度低,易于工程应用。

1 OTA算法原理

基于目标在空间能量谱中呈现的峰值特征,若可得到目标峰值附近的噪声基底高度并以此为检测门限,则可根据目标峰值高于噪声基底的特点实现目标检测,不仅可以使门限值适应复杂多变的背景高度,且可提高对强目标旁瓣的压制效果。本文借鉴OTA算法进行空间谱背景高度的估计原理[20]：

1)输入多波束数据。假设共有N个波束,每一时刻得到N个角度上的空间能量谱数据,记为{X(i)|i=1,2,…,N}。

2)去除边缘效应。在角度轴上设置一个滑窗,K为滑窗半径(表示滑窗包含波束的个数的一半,是一个常整数),角度分辨单元编号(即波束号)i≤K及i≥N-K范围内的数据,无法位于滑窗中心,为保证边界上的波束有足够数据进行背景估计,需将原数据集扩展为X(K+1),X(K),…,X(2),X(1),…,X(N),X(N-1),…,X(N-K),将扩展后的数据重新编号为Y(1),Y(2),…,Y(N+2K)。

3)滑窗取值。将窗长为2K+1的角度轴滑窗在步骤2中的数据集中滑动,滑窗内的数据从小到大重新排列为y(1),y(2),…,y(2K+1)。

4)背景高度估计。用截断平均值作为背景高度估计值：

(1)

式中：α是一个常数,被称为调节系数。yo就是OTA算法估计得到的背景高度,由式(1)可知,除具体输入波束域数据外,yo只跟α和K有关。

5)背景均衡。将不同角度上的空间谱值与yo值进行比较,并作如下处理：

(2)

通过式(2)去掉背景并保留可能存在目标的波束数据,达到背景均衡和压缩动态范围的效果。

OTA算法采用逐帧处理的方式,通过截断平均实时估计背景高度,达到压缩动态范围、突出弱目标和增强图像质量的目的,为后续目标检测与跟踪提供更有利条件,但该算法保留的非零数据中仍不可避免存在大量来自背景而非目标的波束数据,可将背景均衡的结果看作未进行参数估计的高虚警率检测结果,主要用于改善方位历程显示效果,便于人工检测及启动跟踪。此外,α与K的选取对背景估计值yo会产生明显影响,需一定的先验知识来手动设置值α与K值,由于传统OTA算法中的α与K值是两个定值,当均衡效果变差时需人工修改,这限制了OTA算法的工作效率和工程应用。

BSTAD算法针对OTA算法处理结果中存在高虚警和对α与K的参数敏感性带来的不易应用问题,通过分析α与K对yo估计的影响,设计了K随波束舷角变化自动选取和α随空间谱强度变化自动选取方法,达到无需人工干预的自动检测目的。此外将算法与波束内插相结合,不仅为波束内插提供了精确的引导波束来避免波束选取偏差,而且将宽带空间谱提供的波束域数据解算为具有精确角度参数的目标信息,可为后续目标跟踪提供更加准确和可靠的检测结果。

2 BSTAD算法原理

2.1 K对yo影响分析与自动选取

为降低目标自身能量强度对截断均值的计算影响,K一般要大于波束宽度。若K小于波束宽度,进行截断平均时,截取的数据都将来源于主瓣,会导致yo估计过高而漏掉窗内目标,如图1中目标1的检测滑窗选取过小,会造成截断平均数据均来源于目标1的主瓣,因此yo可能高于目标1使其被剔除;过大的滑窗长度易因周边较高背景或附近高信噪比目标的影响导致yo估计值过高,易漏检窗内弱目标,例如图1中目标2的滑窗长度选取过大,其背景高度估计值将受左侧较高背景和右侧目标3的影响而偏高。因此K值选取主要受波束宽度与背景起伏的双重影响。针对背景起伏和强弱目标干扰造成的影响,可在K满足大于波束宽度的前提下尽可能选择小值。下面着重分析波束宽度对K值选择的影响。图1中K1、K2分别为两个滑窗的半径。

图1 角度轴滑窗Fig.1 Angle axis sliding window

以均匀线列阵为例,阵列的主瓣宽度在不同舷角上是不同的,水声中一般以-3 dB波束宽度衡量阵列主瓣宽度,均匀线列阵-3 dB波束宽度2θ-3 dB的表达式[21]为

(3)

式中：λ为分析频段中心频率对应的波长;d为阵元间距,为避免在0°～180°舷角范围内出现模糊扇面,d一般取0.5λ;θs为波束指向对应的舷角。由式(3)可知,越靠近阵列两端,2θ-3 dB越大,正横方向的波束宽度最小,因此传统OTA算法中将K设为常数是不合适的,K应随波束宽度在不同舷角上的变化而改变且至少大于一倍的2θ-3 dB,以此为依据分析K随θs变化的关系,若波束扫描间隔为Δθ,那么不同舷角的波束所占角度分辨单元个数为2θ-3 dB/Δθ,因此K关于θs的表达式可写为

(4)

式中：round(·)是四舍五入取整函数,用来保证K取值的整数性;γ为一个常系数,用来控制K与主瓣宽度的比例关系,由2.1节分析可知γ≥1,文献[19]中指出为保证较好均衡效果,K可取两倍主瓣宽度,因此γ可取2。

2.2α对yo影响分析与自动选取

调节系数α的选取较为困难,至今未有明确理论依据的解析式确定α的取值。在背景均衡算法中该值一般取值1.0～1.1,背景均衡算法允许保留背景信息,这使α一般十分接近1.0,因此背景均衡后存在大量非零背景数据,若直接将这样的结果作为检测结果是不可接受的。分析式(1)可知,K值通过影响输入数据长度影响yo,但二者之间并没有直接的比例关系,而yo与α呈正比,因此可以通过控制α的大小来控制yo进而控制原始波束域数据的保留。当波束内目标信噪比较高时,目标峰值与背景对比明显,需抬高门限来避免检出背景和旁瓣,此时应提高α来使yo增大;当波束内目标信噪比较小时,目标峰值高度与背景较为接近,但弱目标旁瓣一般会与背景融为一体,此时为保证对弱目标有较高的检测概率应降低门限,应减小α来使yo减小。因此可建立信噪比与α的映射关系,通过信噪比变化控制α的调节,实现对yo的有效调节。实际情况下,拖曳线列阵的空间谱中是否存在目标以及目标方位如何正是目标检测的目的,因此实际目标的信噪比是不可得的。这里利用空间谱强度比的概念来近似代替信噪比,角度轴滑窗取出的数据集为ψ={y(m)|m=1,2,…,2K+1},那么窗中心对应波束的空间谱强度比为窗内最大值与yo的比值,若空间谱数据以dB为单位,则空间谱强度比表达式可写为

RSN=max (ψ)-yo|α=1

(5)

式中：yo|α=1是α=1时的yo。

由于相邻两个波束所对应的滑窗仅在角度轴上向右更新了一个值,并剔除滑窗最左侧的一个值,因此相邻波束所采用的RSN估计数据集有较高的重合度,即相邻的多个波束可能具有相同或接近的RSN,这样可以使旁瓣所在角度分辨单元仍与目标峰值位置处的分辨单元有相同的RSN,从而避免将旁瓣视为弱目标而降低门限将其检出,但若滑窗内强弱目标同时存在时(如图1中目标2、目标3所示状况),仍不能避免对弱目标的漏检风险。

为使α随RSN的增大或减小而增大或减小,这里采用简单易实现的一次函数线性映射关系将归一化RSN与α建立联系：

(6)

式中：αmin与αmax分别是α的取值下限与上限;RSNmin与RSNmax分别为RSN的下限与上限。α与RSN的上下限需根据蒙特卡洛仿真实验选择满足虚警概率和检测概率条件时的α与RSN取值范围,本文在后续的仿真实验中叙述了该值的选取方式。

2.3 角度精确估计

相邻波束因存在重叠区,会接收到同一个目标的辐射噪声,使目标在方位历程图中呈现出一定的宽度,过门限检测时同一个目标会出现横跨多个角度分辨单元的检测结果,使检测无法给出目标或疑似目标的准确角度。传统方法需在空间谱或方位历程图上手动选取目标所在的大致波束进行精确测向,手动选取目标所在波束不仅效率低下,且存在引导波束选取偏差,易使舷角估计误差增大。

为避免检测结果的跨波束问题和精确测向时波束选取偏差带来的测向误差,在进行门限检测前,先对空间谱进行逐帧局部峰值检测,某波束的空间谱值大于左右相邻波束空间谱值即可判断为峰值,之后将检出的峰值对应的空间谱与门限yo作比较,超过yo认为是目标,低于yo舍弃。局部峰值检测实际是对目标舷角的一次粗测,一般空间谱值最大的波束是指向目标最准确的波束,该步骤使检测结果仅保留最接近目标来波方向的波束,避免了检测结果的跨波束情况。

BSTAD算法的局部峰值检测步骤实现了目标舷角粗测,但仍存在较大的测向误差,因此将局部峰值检测的结果进行进一步的精确测向是有必要的,因为BSTAD算法给出的粗测波束就是目标所在波束,所以算法可为精确测向算法提供准确可靠的引导波束,将算法输出作为精确测向引导角可避免引导波束选取偏差的产生。基于常规波束形成的精确测向算法有波束内插法和互谱法,互谱法采用分裂阵进行波束形成,需调用阵元域原始数据,这会使算法复杂度和调用数据量大幅增加,丧失了基于宽带空间谱检测算法的调取数据量小、简单易实现的优势,波束内插只需调用宽带空间谱即可实现精确测向,与检测算法使用的数据相同,因此采用波束内插进行角度精确估计。

波束内插利用了主瓣呈现抛物线形状的特征,采用了三点确定一条抛物线的原理,通过抛物线方程计算最大值点对应的角度作为估计值,设空间谱中3个相邻的波束,指向舷角从小到大分别为引导角左相邻波束角θl、内插引导角θc、引导角右相邻波束角θr,其宽带空间谱值分别为X(θl)、X(θc)、X(θr),文献[22]给出了角度估计表达式：

(7)

三点确定一条抛物线时要求中间点对应的函数值是三者最大的,否则抛物线不唯一,局部峰值检测恰好使检测点满足该条件。

检测峰值点来源于目标时,精确测向角度就是目标所在的舷角;检测峰值来源于背景噪声时,三点仍可确定一条抛物线,且抛物线峰值位置与内插引导角相差最大不会超过Δθ,因此虚警点内插对最终检测结果影响不大,对每一帧超过门限的峰值点波束内插后的角度就是BSTAD算法的检测输出。

2.4 BSTAD算法流程

BSTAD算法是帧处理算法,每一帧空间谱数据输入算法时,首先需进行局部峰值检测,筛选出空间谱曲线上的所有峰值;根据峰值所在波束对应的舷角计算该波束的K值,依据K值建立滑窗进行取值,之后根据式(5)、式(6)选择该波束对应的α值;利用OTA算法中的步骤2、3、4计算该波束对应的yo,然后令峰值点的空间谱数据与yo进行比较。若峰值空间谱大于yo,则保留该峰值并送入波束内插算法进行精确测向作为检测输出,遍历该帧所有峰值点得到该帧的全部检测输出,并进入下一帧的检测。整个检测算法流程用图2所示。

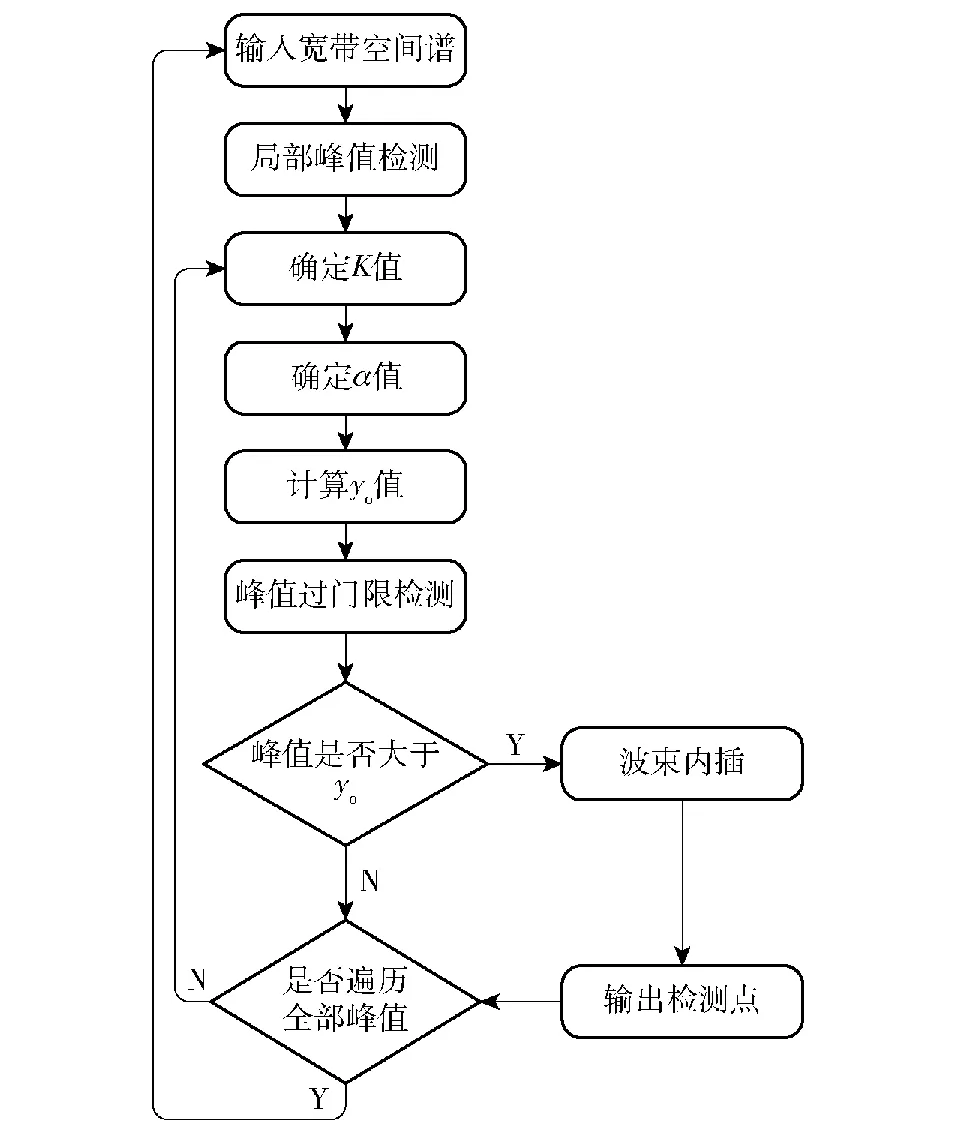
图2 BSTAD算法流程Fig.2 BSTAD algorithm flow

3 算法仿真分析与实验数据验证

3.1 α与虚警概率关系曲线仿真

仿真条件：以64元拖曳线列阵为例,阵元间距2.15 m,频段范围300～400 Hz,采样频率8 kHz,快拍数为8 000,Δθ为1°。令α从1变化至2,通过10 000次蒙特卡洛实验计算阵列仅接收高斯白噪声时BSTAD算法的虚警概率(本文中的虚警概率指所有蒙特卡洛仿真的无目标波束内超过门限的峰值个数之和与全部峰值个数之和的比值),得到的虚警概率曲线如图3所示。

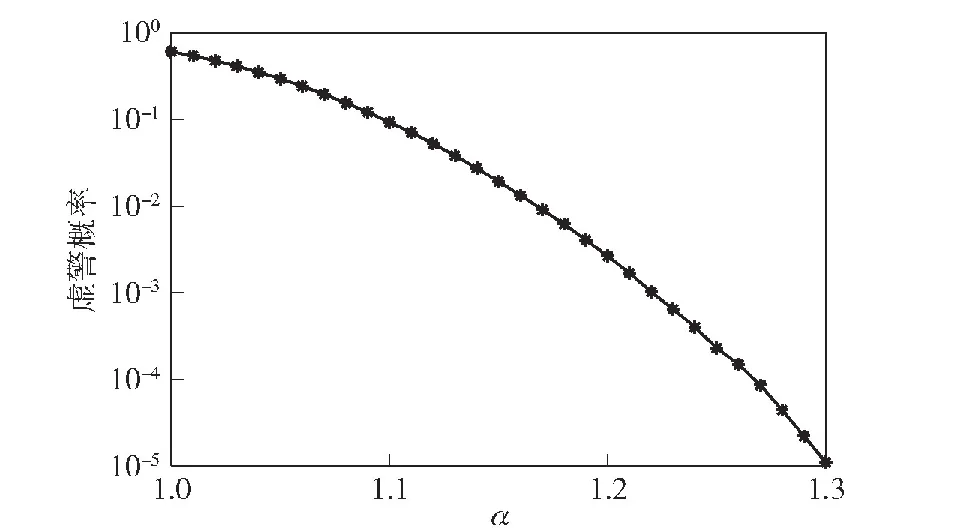
图3 虚警概率随α的变化曲线Fig.3 Curve of false alarm probability varying with α

图3纵坐标采用了以10为底的对数坐标,虚警概率随α的增大而迅速减小,当α≥1.27时,虚警概率降低至0,因此α≥1.27的区域不能在对数坐标轴上画出。当目标波束域信噪为0 dB时,目标与背景噪声强度相同,在空间谱中目标被淹没在背景起伏中,因此该曲线也可视为波束域信噪比为0 dB的目标检测概率随α的变化曲线。该曲线为调节下限αmin的选取提供了依据,若要满足虚警概率在任意信噪比下均低于10-2,则根据曲线可知α>1.17,因此可取αmin=1.18,同时该曲线说明OTA算法用作背景均衡与用作检测时α的取值范围是不同的,因为背景均衡允许结果存在高虚警,而检测则要求低虚警。

3.2 α对检测概率影响仿真分析

通过蒙特卡洛仿真实验分析α对不同信噪比下目标检测概率(检测概率指所有蒙特卡洛实验有目标的波束内超过门限的峰值点个数与蒙特卡洛仿真实验次数的比值)的影响。仿真条件：阵列参数与3.1节保持一致,α变化范围为1.2～1.5,信号舷角为90°,阵元域信噪比(后续信噪比若不说明均指阵元域信噪比)变化范围为-30～0 dB,通过10 000次蒙特卡洛实验计算不同α和不同信噪比下的检测概率,得到如图4所示检测概率曲面。

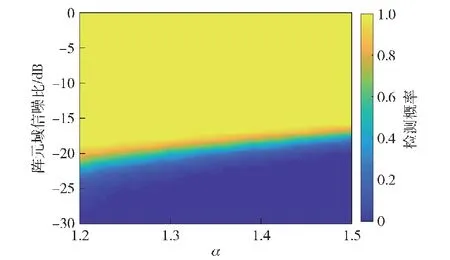
图4 检测概率Fig.4 Detection probability

仿真结果表明在1.17～1.50范围内,随α的增大,算法检测概率从1到0的过渡区逐渐向信噪比升高的方向平移,整个过渡曲面呈现向0 dB倾斜的斜面状态,该曲面为αmax和RSNmax的选取提供了参考。若要求对-20 dB及以上信噪比的目标检测概率大于0.9,则由曲面可知α≤1.3,可取αmax=1.3。在1.18≤α≤1.30区域内平均过渡区宽度约为 5 dB,因此可取RSN的上下限之差为5 dB,因RSNmin=0 dB,所以可取RSNmax=5 dB。

3.3 K对虚警概率影响仿真分析

仿真条件：阵列参数与3.1节保持一致,令K从4变化至20,通过10 000次蒙特卡洛实验计算阵列仅接收高斯白噪声时不同K值下检测结果的虚警概率,结果如图5所示。

图5 不同K值的虚警概率Fig.5 False alarm probability curves for different K values

从图5中可以看出,随着K的增大,虚警概率有略微升高,之后基本稳定在10-2附近,可以认为K与虚警概率没有直接关系,说明2.2节K并不直接影响yo大小的分析是正确的,从侧面印证了式(4)所表达的在阵列参数确定后K值仅与波束舷角有关的结论是正确的,且验证了3.1节αmin选取的有效性和α自动选取方案的有效性。

3.4 K对检测概率影响仿真分析

仿真条件：阵列参数与3.1节保持一致,令K从4变化至20,令目标舷角从10°变化至90°,信号信噪比-20 dB,通过10 000次蒙特卡洛仿真实验计算目标检测概率,结果如图6所示。由于波束与线列阵法线的夹角越大,波束宽度越大,小K值会因滑窗长度过小而使滑窗内源于目标的空间谱值越多,yo估计越大,因此随K值减小,检测概率为0的舷角范围越大;随K值逐渐增大,yo估计值越接近真实背景高度,目标被检出的概率越高,但随着随K值逐渐增大,yo趋于稳定,因此检测概率为1的覆盖范围在舷角轴上增大趋势逐渐平缓,检测概率逐渐趋于稳定,因此若场景中仅有一个目标,K越大越好。

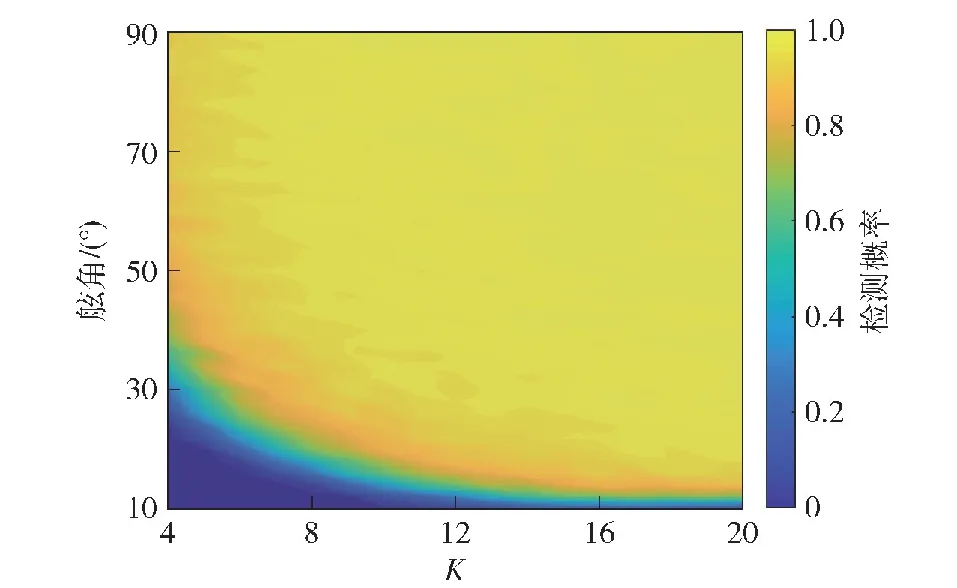
图6 -20 dB信噪比时的检测概率Fig.6 Detection probability at -20 dB

3.5 BSTAD算法α值自动选取有效性分析

仿真条件：阵列参数与3.1节保持一致,产生一个舷角为90°的宽带信号,信号阵元域信噪比范围为-40～0 dB,通过10 000次蒙特卡洛仿真实验计算α自动调节(调节参数按照3.1节、3.2节中选取结果设置)以及令α固定时的检测概率。由于目标舷角固定,包含目标的滑窗半径K不变,因此K自动选取与固定时的检测概率相同,所以本节仿真时K均为自动调节,多种情况下的检测概率曲线与虚警概率曲线分别如图7和图8所示。

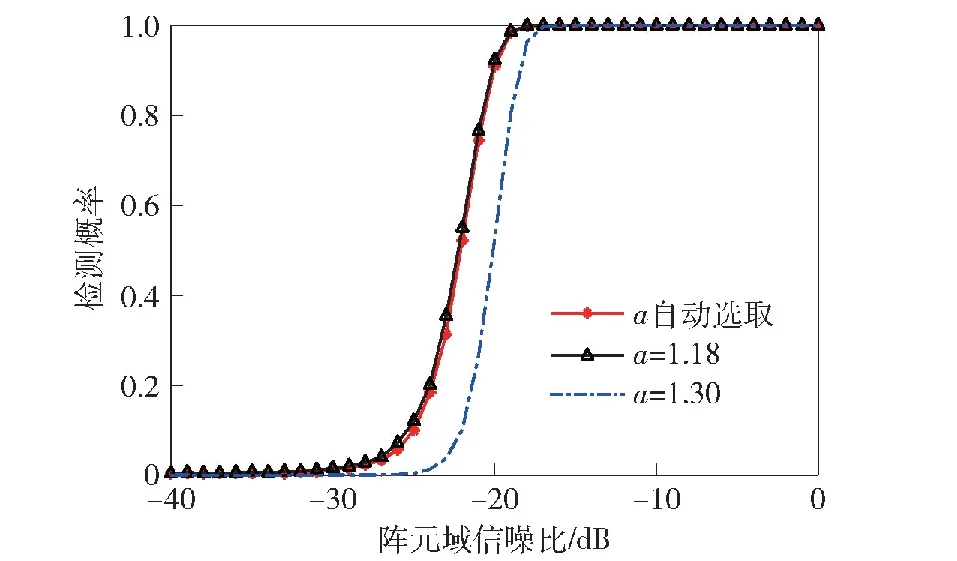
图7 不同α值的检测概率Fig.7 Detection probability curves for different α values

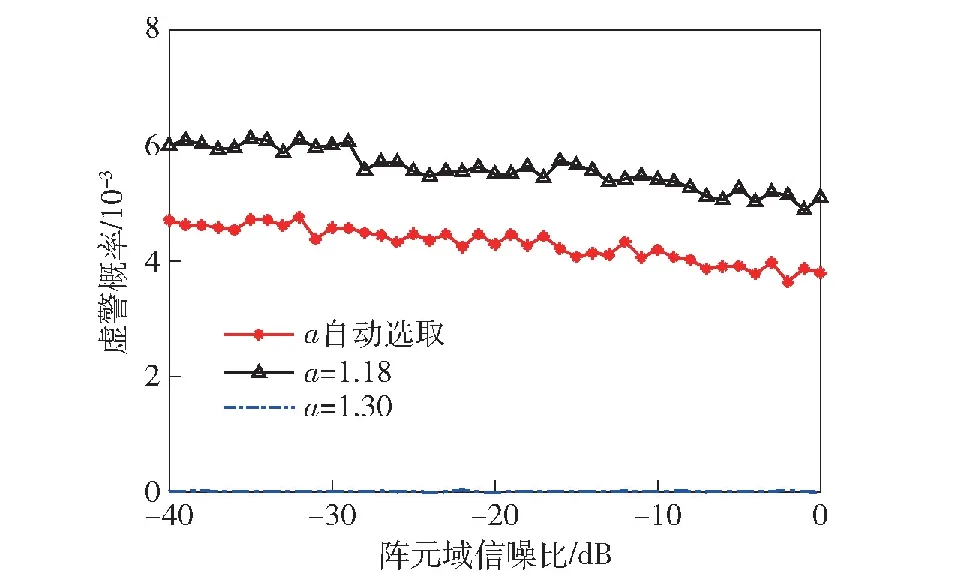
图8 不同α值的虚警概率Fig.8 False alarm probability curves for different α values

由图7、图8可以看出：α自动选取时的检测概率曲线与α=1.18时的结果基本重合,但在信噪比低于0 dB时,前者的虚警概率明显低于后者;α=1.30时的虚警概率最低,这恰好与3.1节中的结果对应,但该情况下的检测概率曲线与α自动选取相比,明显右移,检测概率降为0的信噪比前者比后者高了5 dB。由两图可知,α自动选取方案相较于α固定方案在相同检测性能的前提下,有更低的虚警概率。

3.6 BSTAD算法K值自动选取有效性分析

建立K值与θs关系式的意义在于保证滑窗半径正确选取的前提下减小强目标对临近弱目标所在波束yo估计值的影响。仿真条件：阵列参数与3.1节保持一致,在10°～170°舷角范围内每隔10°生成一个宽带信号,90°舷角处的目标信噪比为0 dB,该目标与其余舷角上目标的信号幅度之比均为5∶1。用于模拟强目标对周边弱目标的影响,常规波束形成的方位历程图如图9所示。分别采用BSTAD算法K自动选取与固定K值时的逐帧检测结果作对比,结果如图10所示。从检测结果中可以看出K=5时,避免了90°舷角处目标与80°、100°处目标位于同一角度滑窗中,因此强目标未对弱目标检测产生影响,但因滑窗选取过小,使10°、170°处目标yo估计过大而漏检两目标。随K逐渐增大,靠近阵列端部的10°、170°处目标逐渐检测出来,但由于K过大,使得正横方向的强目标与两侧的弱目标进入同一角度滑窗,从而使弱目标的yo估计受强目标的影响而偏高,造成漏检。而K自动选取情况下,所有目标均被检出,说明该算法不仅保证K值随波束舷角的不同而自动调节,且有效降低了强弱目标位于同一滑窗内的概率,提高了临近强弱目标的分辨能力。实际上,BSTAD算法可检出两目标的最小角度间隔受空间谱的角度分辨力。滑窗宽度以及目标强度之比的三重影响,由于角度滑窗的存在,BSTAD算法必然会影响两个不等强度目标的角度分辨力,在本节条件下仿真发现,在阵列正横方向上,等强度目标被BSTAD算法检出的最小角度间隔与空间谱角度分辨力相等,均为2°;而对于幅度比为5∶1的两个目标,被BSTAD检出的最小角度间隔上升至5.7°,小于此角度时弱目标在空间谱上靠近强目标旁瓣位置且高度与旁瓣相近,算法将此弱目标视为目标旁瓣而被漏检。

图9 17个目标的方位历程Fig.9 Azimuth history map of 17 targets

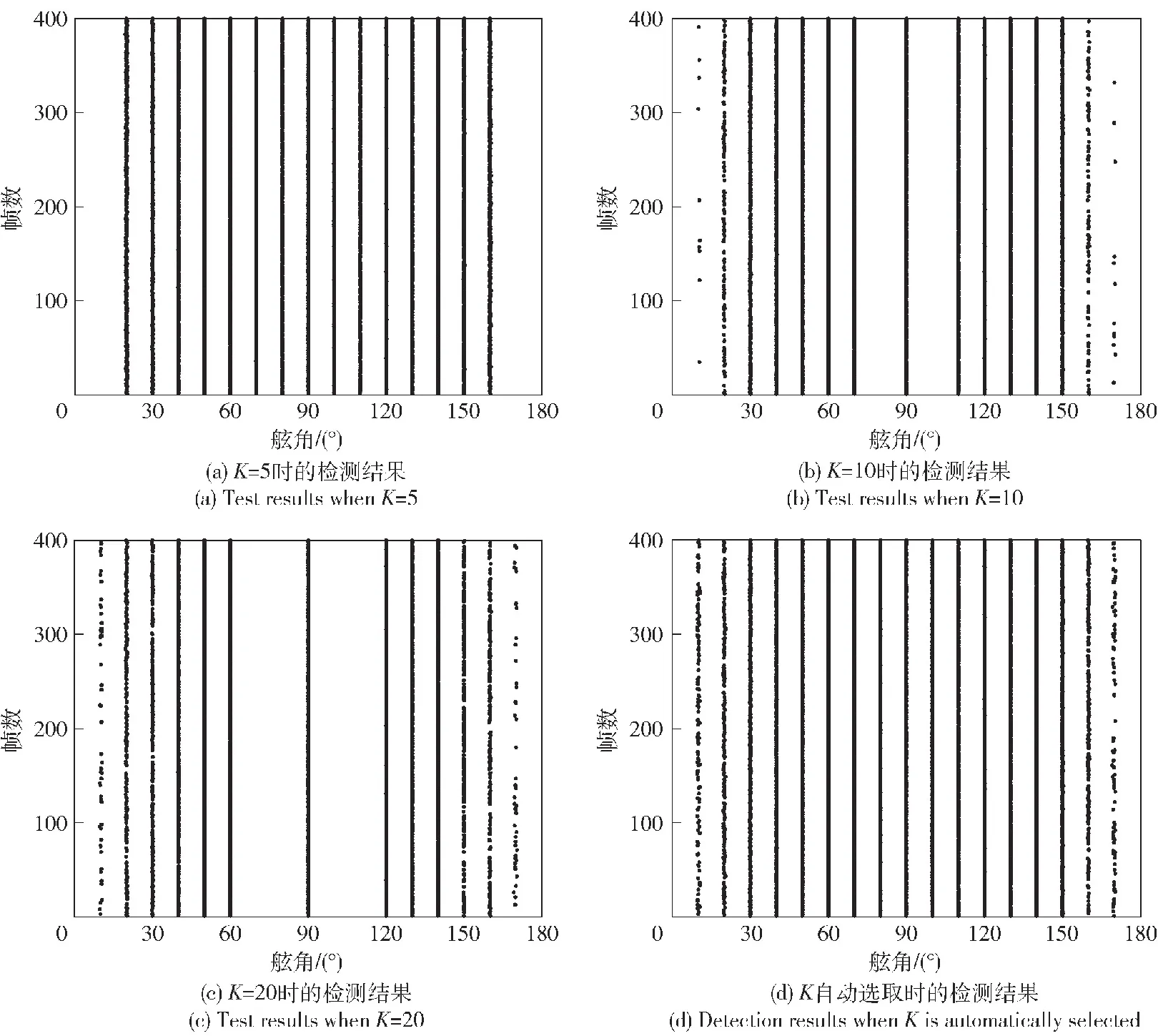
图10 不同K值下的BSTAD检测结果Fig.10 BSTAD detection results under different K values

3.7 强弱目标共存的场景算法仿真

仿真条件：阵列参数与3.1节一致,产生4个信号幅度比为5∶1∶0.5∶0.3的宽带信号模拟目标辐射噪声,舷角分别为-10°、0°、10°、20°。第2个目标信噪比为-10 dB,采用常规波束形成产生400帧空间谱,获得的方位历程图如图11所示。用 BSTAD算法对仿真结果进行逐帧检测,最弱目标(即目标4)检测概率为0.75,令目标4所在波束的全部空间谱值降序排列,选取总长度0.75倍处的值作为固定门限值,对峰值进行固定门限检测,二者检测结果对比如图12所示。

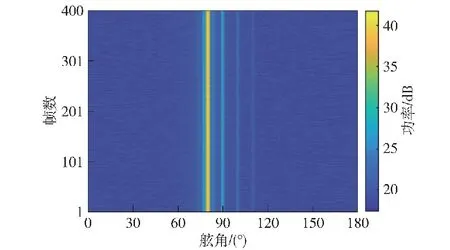
图11 强弱目标共存时的方位历程Fig.11 Azimuth history map when strong and weak targets coexist

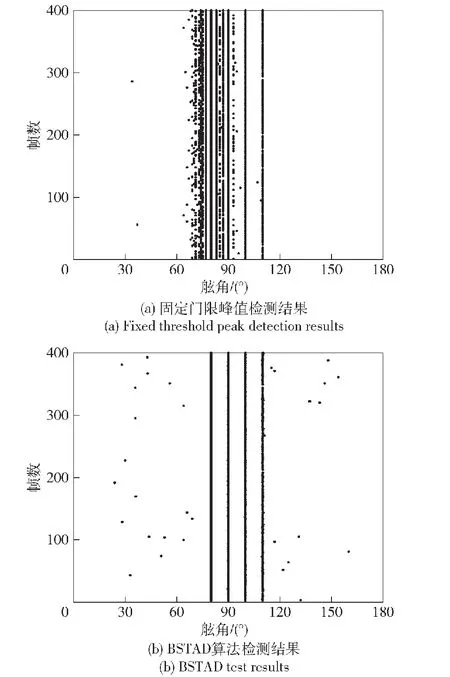
图12 两种不同算法检测结果对比Fig.12 Comparison of test results of two different detection algorithms

强弱目标共存场景中存在门限选取矛盾：高信噪比目标因旁瓣影响会将相邻波束功率抬高,固定门限在任意角度上的门限值均相同,若要提高弱目标检测概率,则必须降低门限,这会检出旁瓣造成虚警概率提升,若要避免检出旁瓣,则必须提高门限值,这会造成弱目标漏检。仿真中两种算法对最弱目标检测概率是一样的,此时由于固定门限选取较低,造成强目标旁瓣被检出;由于BSTAD算法采用了角度轴滑窗,目标第1旁瓣由于距离主瓣较近,因此二者势必会处于同一个角度滑窗中,使得第1旁瓣处的yo值受主瓣影响而偏高,从而避免了旁瓣的检出。因此图12(b)内左侧两个强目标的旁瓣峰值未被检出,虚警率大大降低,由于BSTAD算法逐波束估计背景高度,使得不同波束上的检测门限根据背景高低自适应调整,因此保证了弱目标的检测概率不受强目标影响。二者对比可知,本文提出的BSTAD算法在对弱目标的检测概率相同的前提下,对强目标旁瓣有明显的抑制效果,有效解决了强弱目标共存时检测门限的选取矛盾。

3.8 角度估计误差仿真分析

本节通过对有波束内插、无波束内插及波束内插引导角存在偏差情况下的角度估计均方根误差进行仿真,验证加入精确测向算法的必要性和BSTAD算法对避免引导波束偏差的有效性。仿真条件：阵列参数与3.1节一致,设置目标信噪比为-20 dB、-10 dB、0 dB,舷角为90.5°。因为Δθ为1°,所以该角度恰好不在波束主瓣最大值对应的角度上,通过选取与峰值点相邻的波束角度作为内插引导角来模拟人工选取引导波束进行精确测向时出现波束偏差的情况。通过10 000次蒙特卡洛仿真分析在检测到目标时采用波束内插的BSTAD算法、仅采用局部峰值检测的BSTAD算法和模拟选取引导波束存在偏差时的角度估计均方根误差,结果如图13所示。

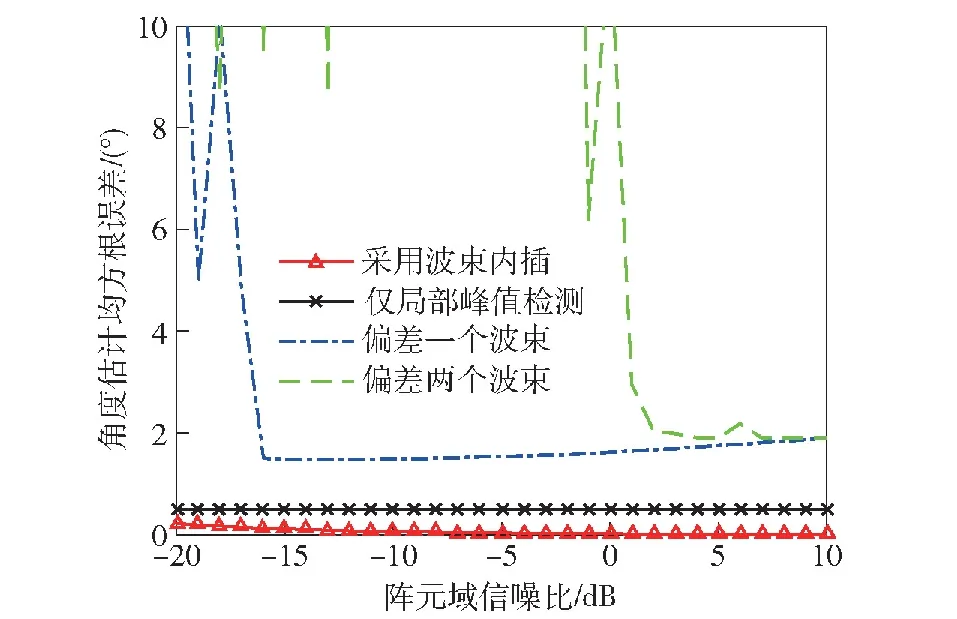
图13 不同情况下角度估计均方根误差Fig.13 Root mean square error of angle estimation in different cases

仿真结果表明：即便仅存在一个波束的选取偏差,仍会产生较大的测向误差,且测向误差随引导波束选取偏差增大而增大;对于仅采用局部峰值检测的BSTAD算法来说,由于与目标舷角最接近的波束包括90°、91°两个波束,与真实舷角相差0.5°,因此检测结果的均方根误差偏差恒为0.5°;采用了波束内插的BSTAD算法检测结果均方根误差最小,随信噪比的变化,均方根误差较为稳定。综上所述,人工选取目标波束进行精确测向不仅效率低下,且结果受选取偏差的影响较大,即便只有一个波束的选取偏差,精确测向结果也会出现较大误差;而 BSTAD算法的局部峰值检测模块可准确找出最接近目标舷角的波束,为后续精确测向提供了准确的引导波束,避免了引导波束选取偏差造成的测向误差增大的问题,且波束内插的加入也有效提高了BSTAD算法的测向精度。因此加入波束内插的 BSTAD算法的检测结果相比人工精确测向的结果更加可靠准确,且算法全程不需要人工参与其中,实现了目标自动检测与角度自动精确估计,效率更高。

3.9 实验数据验证

选取南海某海域的一段拖曳线列阵接收的辐射噪声数据,其空间能量谱图如图14所示。分别用本文设计的BSTAD算法和固定门限算法进行目标检测,检测结果如图15所示。

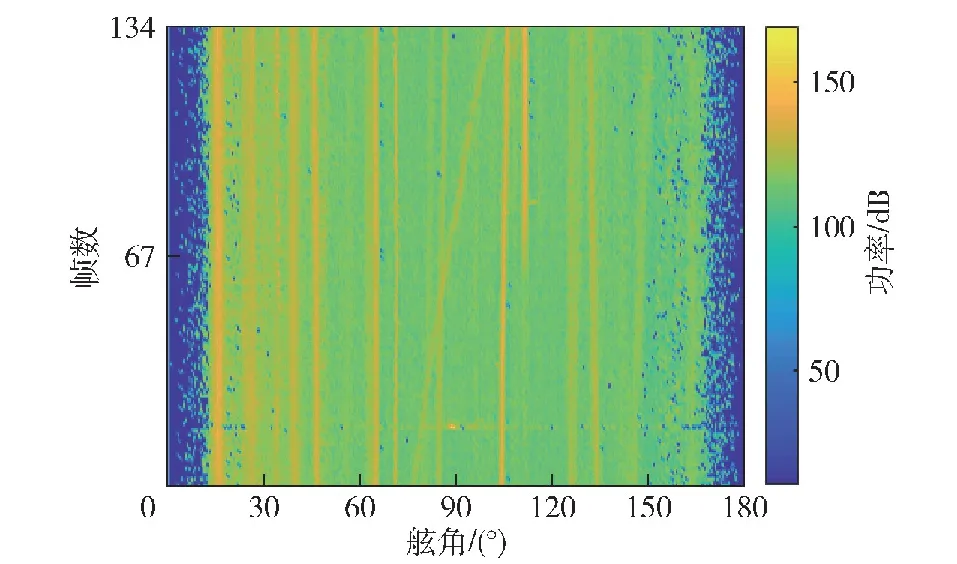
图14 海试实验的方位历程Fig.14 The azimuth history map of the sea trial experiment

由图14可以看出：15°～45°舷角范围内,背景更偏向黄色即背景功率更高,固定门限检测时,该区域来源于噪声和旁瓣的峰值也被检测为目标,因而在图15(a)中该区域虚警较多,轨迹模糊不清、无法分辨,采用BSTAD算法时,该区域内的5个目标检测结果均清晰有效;在55°舷角附近存在一个弱目标,BSTAD算法与固定门限检测相比对该目标有更高的检测概率;在110°舷角附近的目标1～70帧之间信号强度较弱,固定门限检测时该目标1～70帧被漏检,而BSTAD算法对该目标的检测轨迹更完整,在 20帧附近存在沿角度轴的干扰,采用固定门限检测时该干扰被检测出来,而采用BSTAD算法时明显避免了该干扰对检测结果的影响。综上所述,本文提出的BSTAD检测算法对背景在空间和时间上的波动性和不均匀性有较好的适应能力。