考虑故障相关性的复杂二维保修装备机会维修策略
2023-07-10董恩志程中华王荣财张孝娜张月星吴巍屹岳帅
董恩志,程中华,王荣财,张孝娜,张月星,吴巍屹,岳帅
(1.陆军工程大学石家庄校区,河北 石家庄 050003;2.河北省机械装备状态监测与评估重点实验室,河北 石家庄 050003;3.陆军研究院 陆军建设发展研究所,北京 100012;4.94295部队,山东 济南 250000)
0 引言
保修是指装备列装部队后,借助社会资源、依托承制单位技术力量辅助军方开展的装备维修保障工作[1]。随着军事变革不断深入,大批结构复杂、技术密集的新型复杂装备列装部队,极大地提高了部队的整体作战能力,同时也对我军的装备保障能力建设提出了更高的要求[2]。由于新型复杂装备各部件之间存在较为明显的故障相关关系,故障模式更多、故障规律更难把握,因此,当前仅依靠部队自身维修保障力量已难以胜任新型复杂装备的维修保障任务。与此同时,装备承制单位有较为完善的维修设施设备,对新型复杂装备的性能也更为熟悉,因此应探索合理的保修方式将承制单位的技术力量引入新型复杂装备的维修保障中,以弥补部队建制维修保障能力的不足。但在实际运作过程中缺乏科学的保修服务决策方法支持,导致新型复杂装备的保修效果不够理想、军地责任划分不清,造成双方利益冲突较为明显[3]。
新型复杂装备通常由众多的多部件系统组成,保修活动通常针对构成多部件系统的单部件展开。新型复杂装备中,多部件系统的寿命通常受日历时间和行驶里程的共同影响,因此采用二维保修的方式,任一维度的保修期达到预定期限,则保修结束[4]。如某型高炮有长达3 a与250 000 km的二维保修期。在二维保修期内,承制单位还会定期开展预防性维修。预防性维修是指在装备故障前通过故障检查、状态检测、维修或更换等一系列方式防止装备功能故障发生,使装备保持在规定状态所进行的全部活动。实践证明,预防性维修能够有效降低装备非预期故障带来的损失,提高装备的可用度[5]。
尽管军地双方都对新型复杂装备的保修工作进行了较为深入的理论研究和实践,但当前在保修服务决策方面还存在一些问题:一是由于组成多部件系统的各部件故障规律不同,因此孤立地对各单部件进行维修会增加预防性维修的频率和成本支出,另一方面,机械地将各部件的预防性维修工作组合起来会造成部件的预防性维修工作提前,浪费装备的使用价值,导致维修过剩;二是当前的维修计划制定通常是基于经验的,不考虑多部件之间的故障相关性,也缺少定量化辅助决策模型的支持,不利于承制单位控制保修成本,装备可用度缺乏保证。
基于上述分析,本文拟在多部件系统故障相关性分析的基础上,采用不完美预防性维修策略和二维保修方式,依据预防性维修时部件可靠性阈值确定各单部件的不完美预防性维修间隔期,以部件生命周期内单位时间保修成本最低为目标确定各单部件更换周期;采用机会维修的方式,以多部件系统可用度最大为目标,依据机会维修时部件可靠性阈值将各单部件的预防性维修工作组合起来,形成多部件系统机会维修计划。通过遗传算法求解各部件机会维修时可靠性阈值,最后通过对比分析验证本文所提方法的有效性。
1 复杂装备保修研究现状分析
1.1 二维保修研究现状
二维保修的特征是保修期包含日历时间与使用强度两个变量,通常可由二维平面上的一块区域表示,保修政策会引起保修区域形状的变化,Wang等[6]详细梳理了二维保修政策及其对应的保修区域形状。根据保修活动开展的时间不同,二维保修又可分为二维初始保修与二维延伸保修。二维初始保修是指新装备列装后,在二维保修期内的规定时间和规定条件下,承制单位为使装备保持、恢复或改善到规定技术状态所进行的全部活动,通常包括修复性维修工作和预防性维修工作[7-8]。二维初始保修决策通常是以保修成本最低为目标[9-10],部分研究还兼顾了保修期内装备可用度[11-12]。越来越多的研究聚焦于保修政策的制定,通过在制造商和用户之间取得平衡,使制造商和用户都能接受保修政策[13]。与此同时,由于预防性维修可以防止故障或故障的严重后果,减少故障停机造成的损失,因此越来越多的研究开始关注预防性维修[14]。二维延伸保修是指在初始保修期结束后,由承制单位负责开展的后续装备维修保障工作,军方可以决定是否购买延伸保修服务。目前,对二维延伸保修的研究越来越突出用户的异质性,即保修方案是针对不同用户量身定制的[15]。然而,由于在民用产品领域,延伸保修服务提供商负责延伸保修政策的制定,因此目前的大多数研究都是从延伸保修服务提供商的角度出发,以延伸保修成本最低或利润最大为目标,很少考虑用户对产品可用度的要求[16-18]。此外,大多数研究对象都为单部件系统,忽略了多部件之间的故障相关性。
1.2 多部件故障相关性研究现状
一直以来,在国内外的研究中,多部件系统中各部件之间的相关性主要有3种类型:结构相关性、经济相关性和故障相关性。近年来,一些学者将多部件相关性扩展到4种类型:结构相关性、经济相关性、故障相关性和时间相关性。由于故障相关性广泛存在于多部件系统中,因此学者们对其关注较多。故障相关性主要是指在多部件系统中,部件故障的发生会导致系统整体环境的变化,进而影响其他部件的状态,导致故障率的增加[19]。多部件之间的故障相关性可分为3种类型[20]:I类是故障相关,即当一个部件发生故障时,它将以一定的概率(p,0≤p≤1)导致其他部件发生故障;II类是故障率相关,即当一个部件发生故障时,会在一定程度上增加其他部件的故障率;III类与冲击损伤有关,即当系统中的一个部件发生故障时,会对其他部件造成一定程度的随机损伤,当随机损伤累积到一定程度时,会导致部件故障。Sun等[21]引入交互故障概念,建立了部件间故障交互的定量分析模型,给出了基于实验的部件间故障相关系数的推导方法,属于早期的故障相关性研究。Zhang等[22]研究了具有I类故障相关性表决系统的定期检查策略,基于马尔可夫更新过程推导了系统的短期和长期维护费用。韩思远[23]根据风电机组的故障相关性分析和全概率公式,分别计算了该子系统的固有可靠性和综合可靠性,进一步计算了该子系统的故障率,研究了基于子系统故障率的风电机组最优维修方案。钱倩等[24]基于多个部件之间的II类故障相关性,研究了具有单向故障相关的多部件系统预防性维护策略,以预防性维修间隔为决策变量,以规定运行时间内的最小维护成本为目标,建立了预防性维修任务成组优化模型。王红等[25]使用故障链模型来描述部件之间复杂的故障相关关系,以维护时间最短和成本最低为目标,对部件实施不确定周期的成组维护策略,并使用遗传算法优化维护计划。综上所述可以看出,多部件系统故障相关性的研究仍然局限于一维保修方式,没有考虑二维保修方式对保修成本和维修计划的影响。基于上述分析,本文的研究重点是在二维保修的基础上,考虑多部件之间的故障相关性,进行多部件系统的机会维修决策。
1.3 机会维修研究现状
机会维修是指某一部件的修复性维修或预防性维修给其他部件的预防性维修带来机会,从而将部分预防性维修工作提前进行的维修活动。Berg[26]最先在两部件系统的研究中应用机会维修策略。van der Duyn Schouten等[27]提出了适用于两部件串联系统的(n,N)机会维修策略。Zheng等[28]在不考虑各部件故障后维修的条件下,提出多部件系统的机会更换模型。Caldeira Duarte等[29]采用完全维修方式,研究了多部件串联系统的最优预防维修周期。Laggounea等[30]针对多部件连续运转的氢压力机系统,采用蒙特卡洛仿真方法制定了机会维修方案。苏春等[31]研究了风力机的机会维修策略,以节省的总机会维修成本最大为目标,采用滚动窗口方法完成风力机维修活动的动态调整,进而得到风力机的最优预防性维修活动安排。薛朝改等[32]在单部件预防性维修计划的基础上,以维修成本最低为目标,以机会维修系数与部件Birnbaum重要度的比值和系统的可用度满足一定要求为约束条件,建立了多部件系统机会维修决策模型。通过文献综述可以看出,当前研究制定的机会维修方案大多是基于时间维度的,即基于一维保修方式的较多,缺少二维保修方式下多部件系统机会维修决策的研究,更没有研究在进行机会维修决策时考虑多部件之间的故障相关性。
2 模型描述与假设
本文以串联多部件系统为研究对象。令WB表示系统在日历时间维度的保修期,UB表示系统在行驶里程维度的保修期。部件i在二维保修期(WB,UB)内,按照时间间隔Tk,i开展预防性维修,预防性维修包括不完美预防性维修和预防性更换。在单部件预防性维修计划的基础上,借助机会维修时部件可靠性阈值,将各单部件预防性维修工作组合优化,以提高多部件系统可用度,降低保修期内多部件系统保修成本。
模型假设如下:
1)部件初始可靠度为1,即从全新投入使用。
2)部件呈现日历时间和行驶里程两个维度的退化规律。
3)维修资源充足,不考虑因维修资源不足造成等待维修的情况。
4)部件的主要故障模式只有一种,不考虑多个故障模式的情况。
5)使用率可通过历史数据获得,且在初始保修期内同一部队使用率不变,不同部队的使用率服从均匀分布。
6)当部件i运行到最低可靠度要求时,对部件执行预防性维修,同时考虑对其他部件进行机会维修。预防性维修为不完美维修。当进行第ni+1次预防性维修时对其进行更换。
7)在预防性维修间隔期内发生故障,对部件i采取修复性最小维修。不考虑对其他部件进行机会维修。
3 模型构建
3.1 可靠度模型建立
多部件系统内共包含V个部件,采用单变量法中直接构造方法构建单部件二维故障率模型,基于Yun等[33]的构造方法,部件i的故障率函数形式为
λi(t|r)=θ0i+θ1ir+θ2it2+θ3irt2,1≤i≤V
(1)
式中:t为日历时间;r为使用率;θ0i、θ1i、θ2i和θ3i均为表达式参数。根据假设可知,初始保修期内同一部队使用率不变,因此r与t之间的关系为r=U/t,U为使用程度,如里程。确定表达式的参数需要通过统计保修期内一段时间的样本故障时间t和发生故障时的使用程度U来确定λi(t|r)和使用率的分布Gi(r)的具体表达式。参数的拟合过程为:
步骤1选择L个部件,xi代表第i个部件在保修期内的故障次数。计算ri的值,ri=ui,j/ti,j,ti,j和ui,j分别代表第i个部件的第δ次故障时的使用时间和使用程度,1≤i≤L,1≤δ≤xi。
步骤2将所有ri分成M组,第m个区间用[hm-1,hm)表示。绘制ri的概率直方图,通过直方图就可以拟合出使用率的概率密度函数gi(r)。
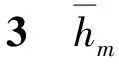
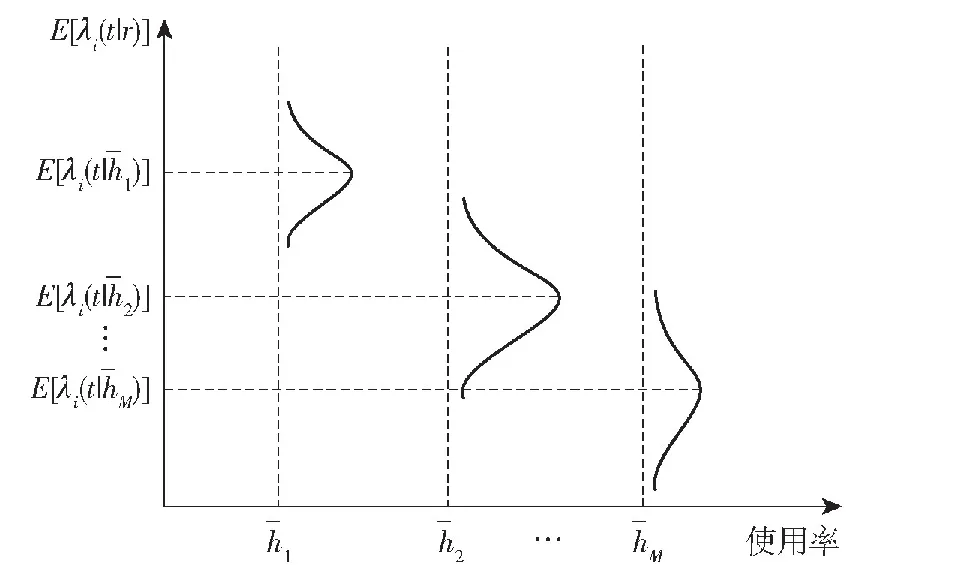
图1 不同使用率下部件故障率函数拟合Fig.1 Failure rate function fitting under different utilization rates
步骤4将所有特定使用率下的故障率曲线在同一三维空间中表示出来,通过这些曲线拟合出三维曲面,便可得到二维故障率函数λi(t|r)。
预防性维修为不完美维修,第k次不完美预防性维修后,也即在第k+1个预防性维护周期内,部件的故障率[34-35]为
λk+1,i(t|r)=αλk,i(t+βTk,i)
(2)
式中:α为故障率递增因子;β为役龄递减因子;Tk,i为第k个维护周期的长度。
由于各部件之间存在故障相关关系,因此采用故障链模型描述部件之间的故障相关关系。在故障链模型中,只影响其他部件而不受其他部件影响的节点叫做故障起点;只受其他部件影响而不影响其他部件的节点叫做故障终点;既受部件影响又影响其他部件的节点叫做故障中点。故障链模型[36]如图2所示。

图2 故障链模型Fig.2 Failure chain model
图2中,A是故障起点,D为故障终点,其余节点则为故障中点。将各部件进行编号,如表1所示。
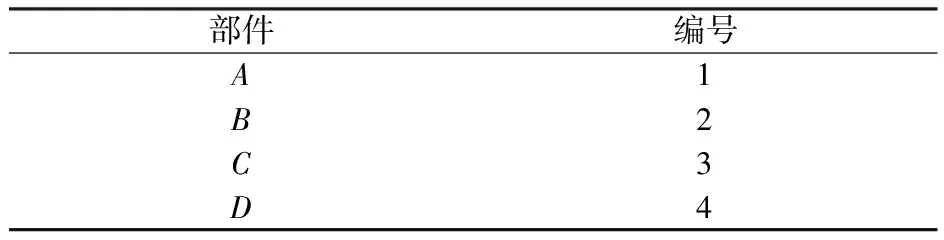
表1 部件编号Table 1 Component number
采用故障相关系数刻画部件之间的故障相关程度,则故障相关系数矩阵χ为
式中:χi1,i2表示部件i2对部件i1的故障影响系数。在由V个部件组成的系统内,考虑部件之间存在的故障相关关系,则部件的实际故障率由两部分组成:固有故障率和相关故障率。则考虑故障相关性的情况下,部件的实际故障率可表示为
(3)
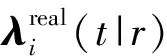
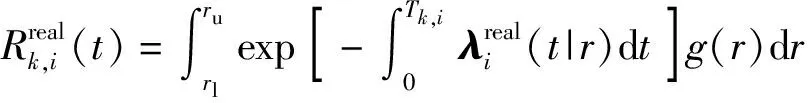
(4)
式中:g(r)代表不同部队使用率的概率密度函数;rl和ru分别为使用率的下限和上限。
3.2 单部件预防性维修间隔期确定
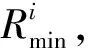
(5)
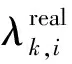
式(5)可以改写为
(6)
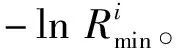
(7)
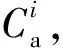
(8)
通过求解式(8),得到最优的Tk,i和ni。
3.3 多部件系统机会维修策略
机会维修策略是指在某一时刻对一个部件进行修复性维修或预防性维修时,将预防性维修时间接近该时刻的多个部件一起维修,从而降低系统总停机时间,提高多部件系统可用度。由此可见,机会维修会调整部件的维修时刻,会导致部件维修时刻的提前,提前维修有一定概率导致维修过剩,造成维修成本的增加和可用度降低。因此,需要控制一定的条件,只有当部件符合该条件时才进行机会维修。
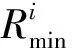
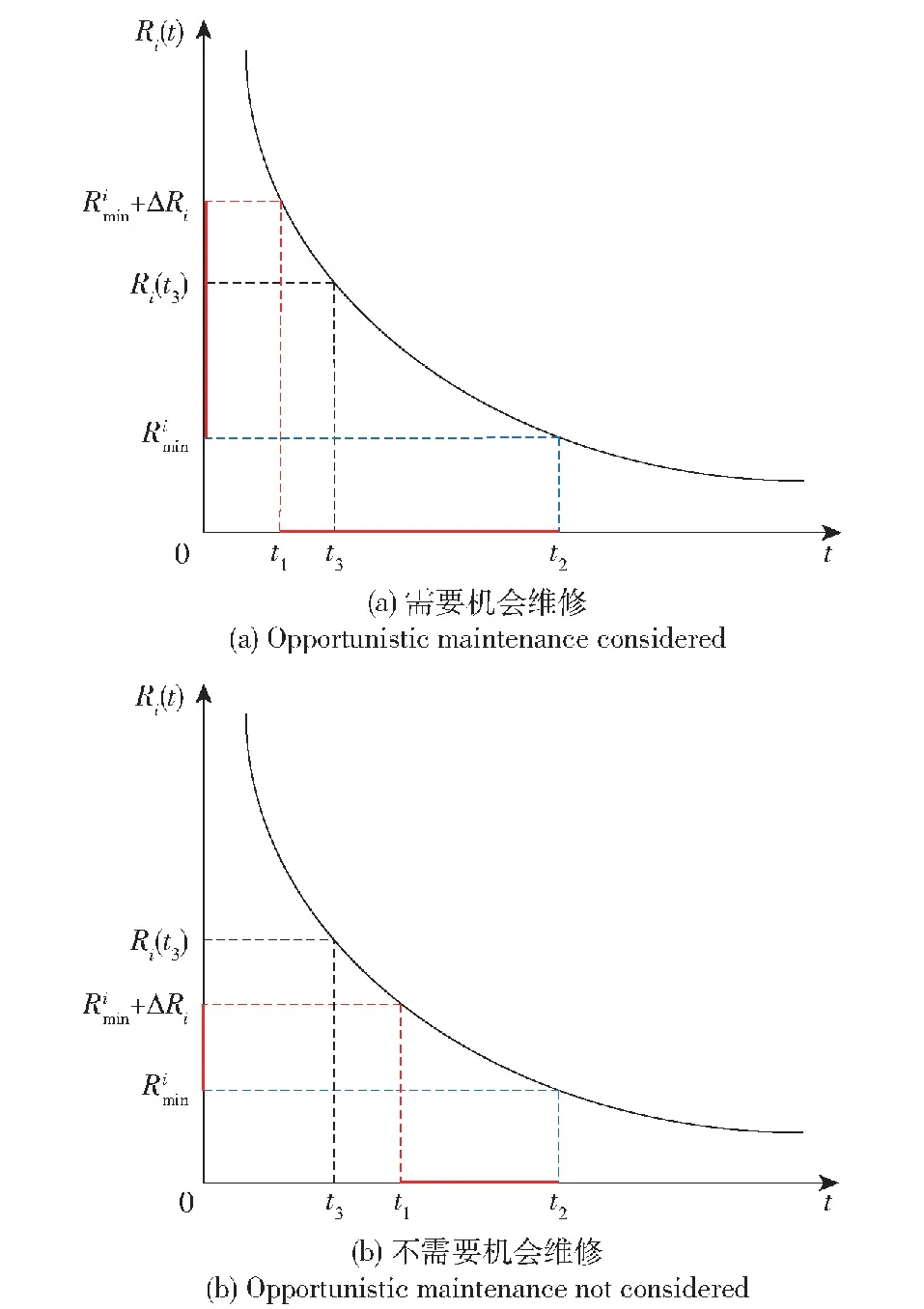
图3 部件可靠度示意图Fig.3 Schematic diagram of component reliability
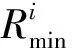
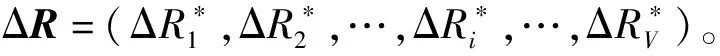
通过3.2节可以求得部件i的生命周期Li为
(9)
同时可以得到部件i每次预防性维修的时刻:
(10)
式中:φi为部件i在保修期内的预防性维修总次数,φi=wi(ni+1)+vi,wi表示部件i在保修期内的预防性更换次数,vi表示部件i在保修期内最后一次更换后直到保修期结束这一段时间内的预防性维修次数。
由于多部件系统采取二维保修方式,二维保修期为[WB,UB]。不同的使用率rz会导致实际保修期发生变化,如图4所示。
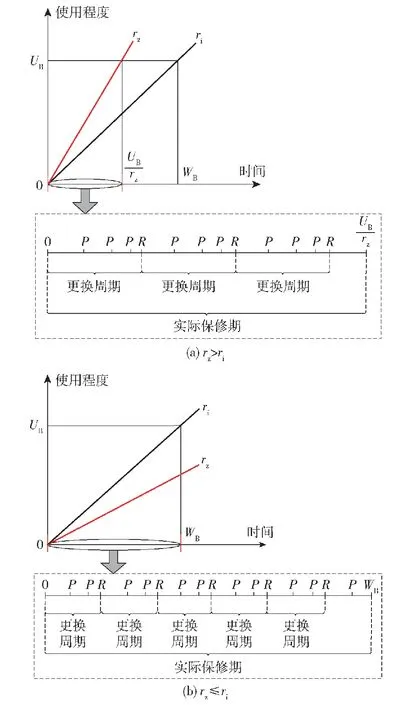
图4 不同使用率下保修期示意图Fig.4 Schematic diagram of warranty period under different utilization rates
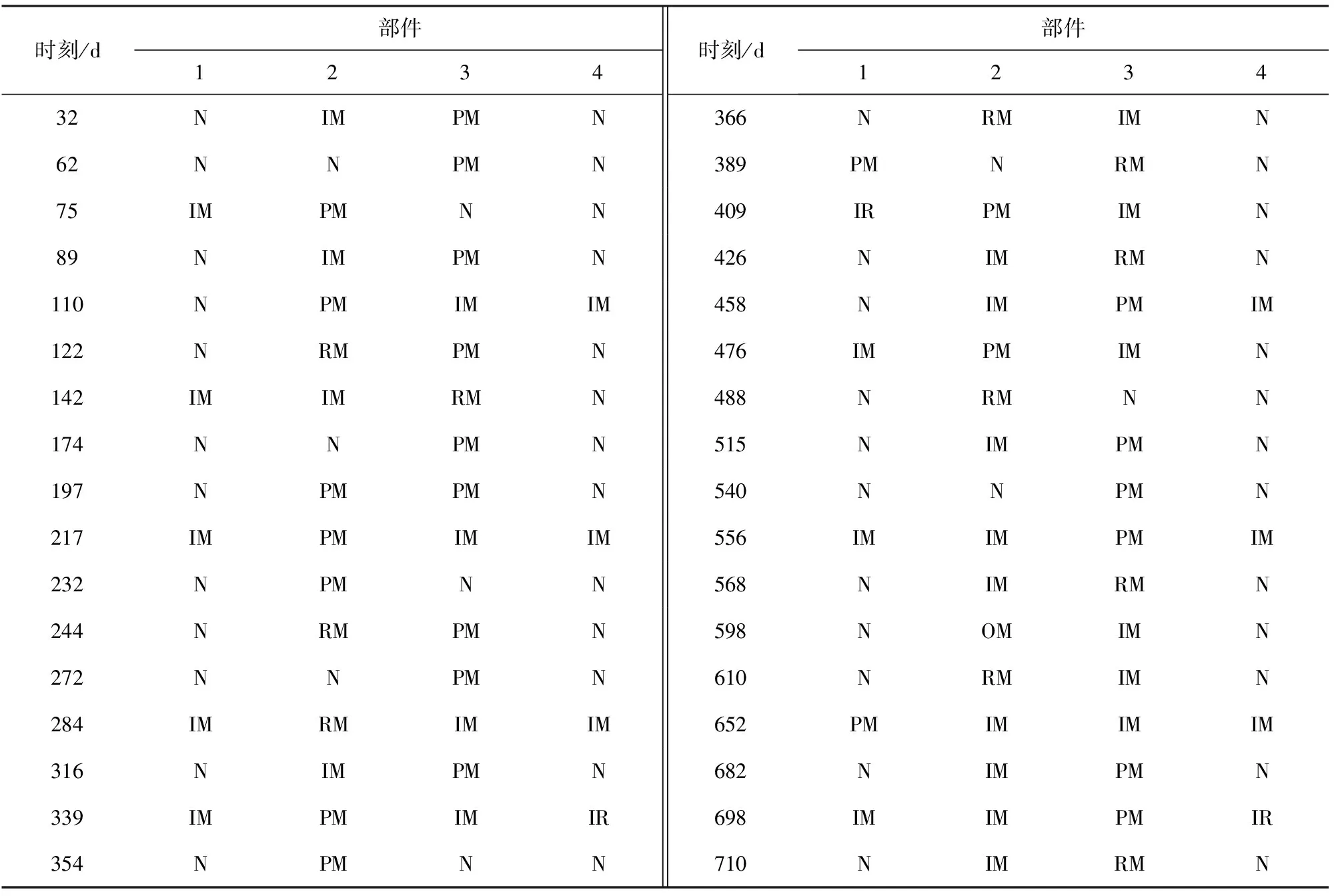
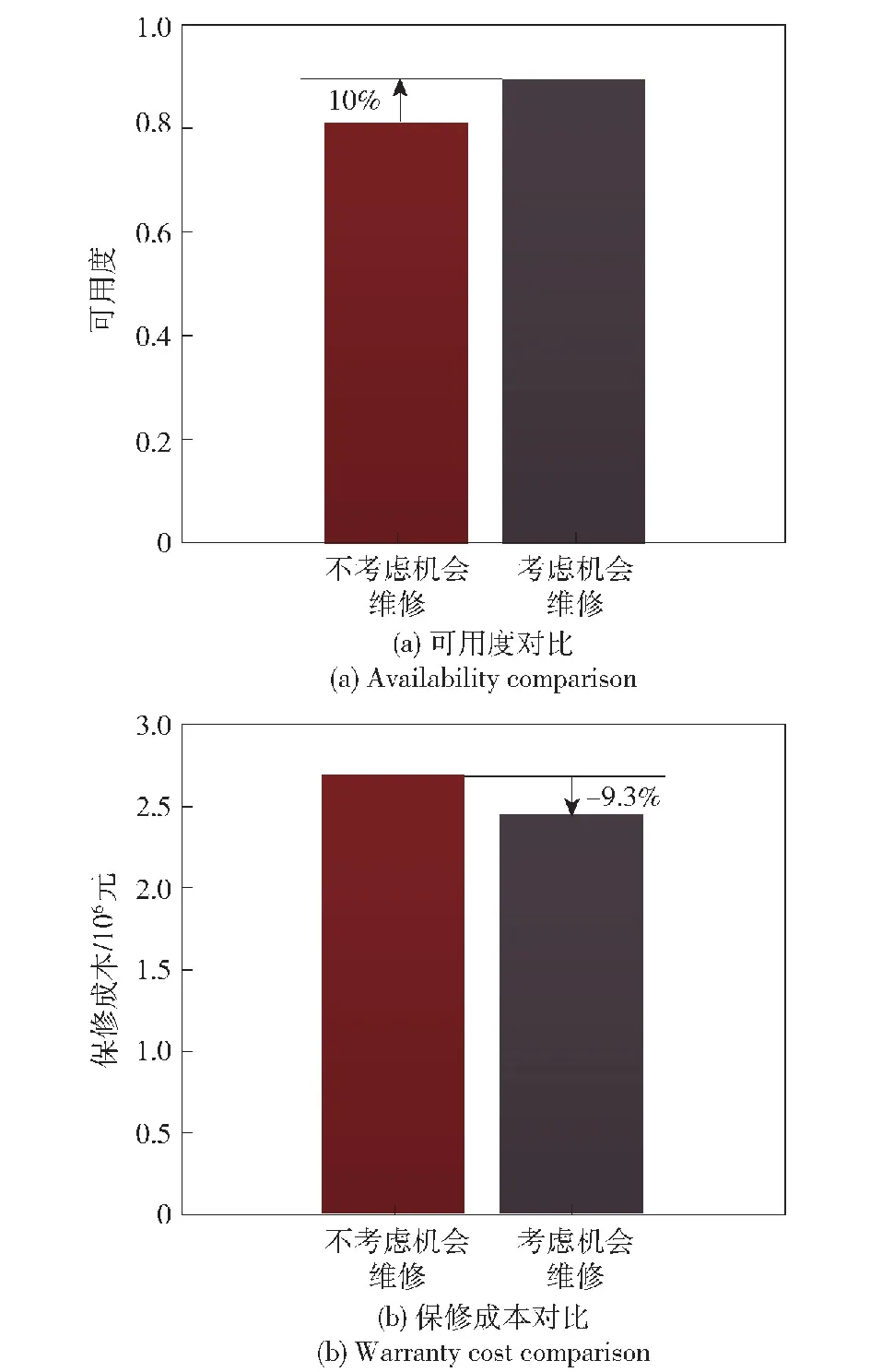
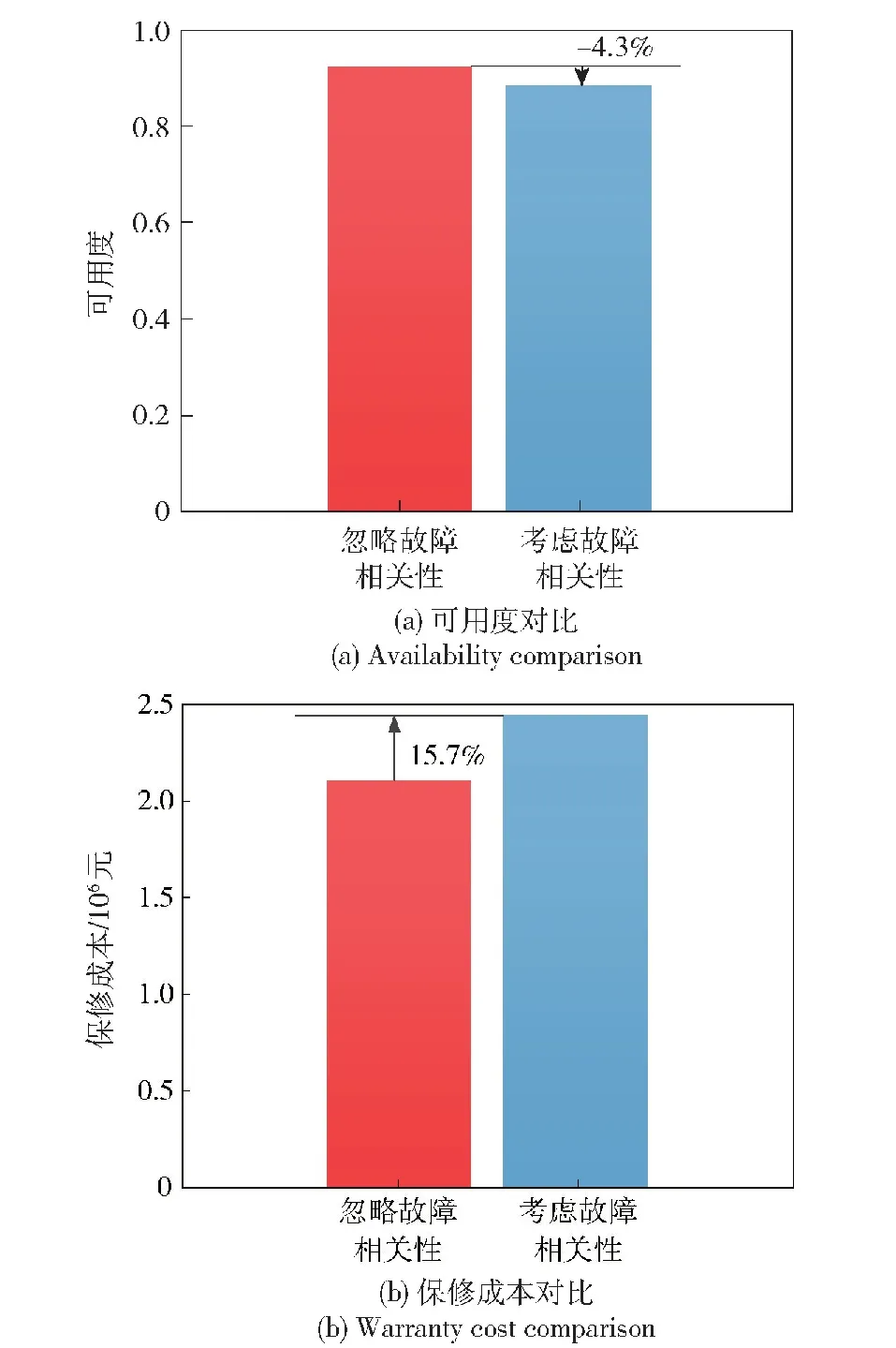
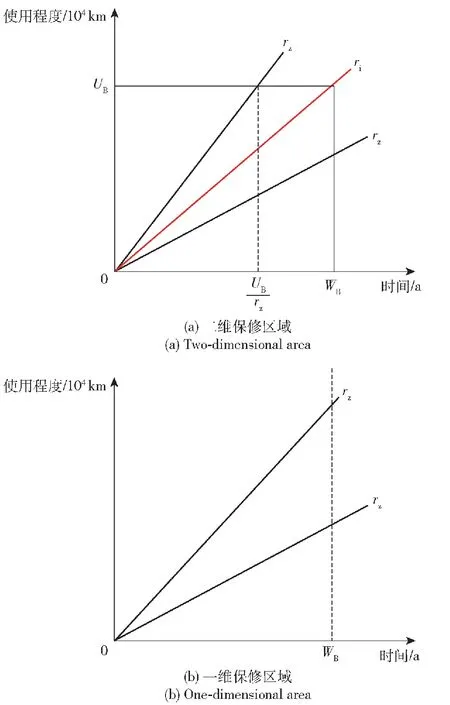
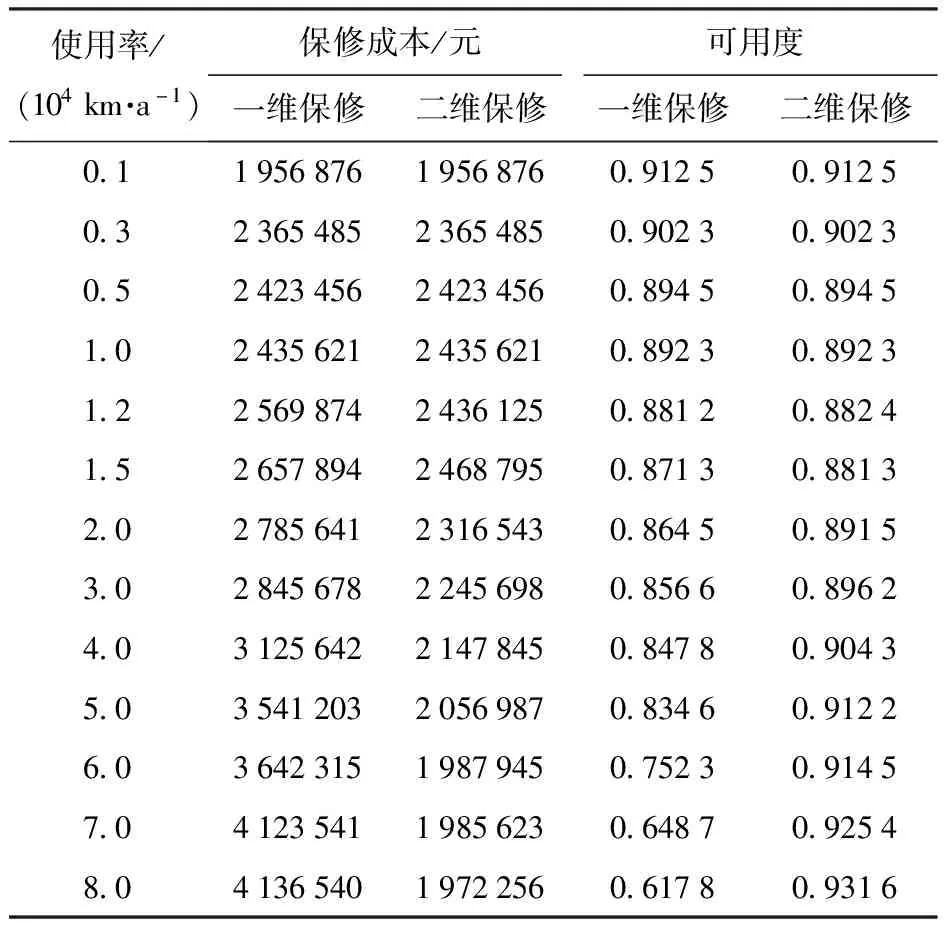
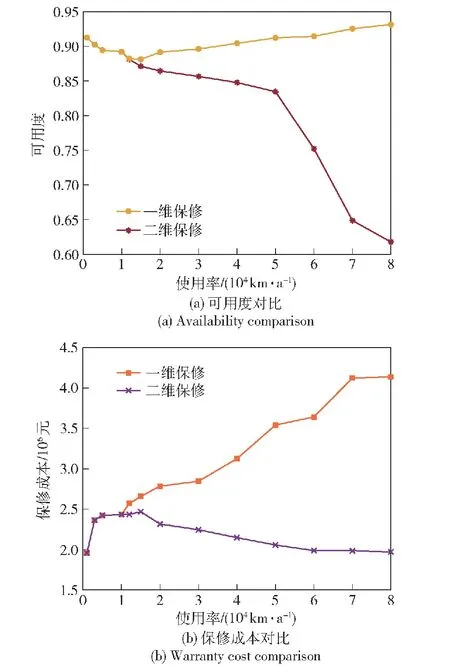
图4中,ri表示初始保修区域的形状参数,即名义使用率,ri=UB/WB。当rz≥ri时,由于使用率较高,保修期在时间维度提前结束,此时部件的二维保修期为(UB/rz,UB);当rz (11) (12) 设多部件系统在保修期内一共进行了Y次预防性维修,每次进行预防性维修的时刻为tsys=(t1,t2,t3,…,ty,…,tY)。假设在多部件系统的第y次预防性维修恰好是部件i第j次预防性维修,部件i的停机时间为 (13) 同时检验是否需要对其他部件进行预防性维修,以部件l为例,多部件系统第y次预防性维修时部件l的停机时间为 (14) 多部件系统第y次预防性维修的停机时间为 (15) 则保修期内多部件系统预防性维修总停机时间为 (16) 保修期内多部件系统修复性维修总停机时间为 (17) 保修期内多部件系统可用度为 (18) 当rz≥UB/WB时,此时保修期在时间维度为[0,UB/rz],可得保修期内的多部件系统可用度为 (19) 多部件系统在保修期[WB,UB]内以可用度最大化为目标的机会维修模型为 (20) 通过求解该模型,得到各个单部件的最优机会维修时可靠性阈值: (21) 根据3.2节确定的单部件预防性维修间隔期,进一步确定各单部件的最优预防性维修计划,进而运用3.3节中的多部件系统机会维修策略求得多部件系统可用度最高时各单部件最优机会维修时可靠性阈值。具体的算法步骤为: 式中:θ1为小区间使用率下限;θ2为小区间使用率上限。 进而将各个单部件预防性维修时刻按由小到大的顺序排列,可得数组tsys=(t1,t2,t3,…,tε,…,to)。 设定各单部件机会维修时可靠性阈值,初始化停机时间为0。设定t0=0,ε=1。 步骤5更新数组tsys。删除在tε时刻提前进行的相关部件的预防性维修时刻,如果tε+1被删除,则将tε后的时刻标记为tε+1。 步骤8返回步骤4,直到ε>o。 步骤11计算多部件系统在保修期内的期望可用度EA。计算公式为 算法流程如图5所示。 图5 算法流程图Fig.5 Algorithm flow chart 某新型装甲突击车动力系统技术结构复杂,维修难度大,初始保修期内主要由承制单位开展修复性维修与预防性维修工作。该动力系统可看作由 4个部件组成的故障相关多部件系统,各部件寿命服从的分布为λi(t|r)=θ0i+θ1ir+θ2it2+θ3irt2,1≤i≤4。 动力系统中的各部件都存在日历时间和行驶里程两个维度退化的趋势:一方面,随着行驶里程增加,动力系统各部件磨损较为严重,这会造成系统故障率增加;另一方面,动力系统长时间不工作重新启动时干摩擦或半干摩擦现象较为严重,会加速部件磨损、退化[37]。因此,日历时间和行驶里程同时影响动力系统的可靠度,预防性维修工作应同时关注动力系统的日历时间和行驶里程。已知该动力系统具有(2 a,2×104km)的二维保修期,保修期内对动力系统的各部件采取定期预防性维修策略,预防性维修间隔期内的非预期故障采取最小维修策略,当各部件的预防性维修达到一定次数时,对其实施预防性更换。各部件的役龄递增因子和故障率递减因子相同,均为α=1.12、β=0.12。4个部件之间存在单向故障相关关系,其故障链模型如图6所示。 图6 动力系统故障链模型Fig.6 Failure chain model of the power system 已知该动力系统的故障相关系数矩阵为 动力系统使用率服从(0.1×104km/a,10×104km/a)上的均匀分布。其余参数设置如表2所示。 表2 参数设置Table 2 Parameter setting 已知该动力系统具有(2 a,2×104km)的二维保修期,一年按365 d计算。首先根据3.2节中的模型,求出各部件的生命周期内单位时间保修成本随预防性维修次数变化趋势,如图7所示。 图7 各部件单位时间保修成本变化示意图Fig.7 Schematic diagram of changes in unit time warranty cost of each component 由图7可以看出,各部件生命周期内最优预防性维修次数分别为6次、4次、5次和3次,对应的最低单位时间保修成本分别为1 082.7元/d、652.2元/d、1 624.7元/d和320.6元/d。 以使用率为1×104km/a为例,在不考虑机会维修时,各单部件在日历时间与行驶里程维度的预防性维修间隔如表3、表4所示。 表3 各部件预防性维修间隔期(日历时间维度)Table 3 Preventive maintenance interval of each component (Time) 表4 各部件预防性维修间隔期(行驶里程维度)Table 4 Preventive maintenance interval of each component (Usage) 根据各部件预防性维修间隔期,可以计算得到使用率为1×104km/a的条件下,则各部件在日历时间与行驶里程维度的预防性维修时刻如表5、表6所示。 表5 各部件预防性维修时刻Table 5 Preventive maintenance time of each component 表6 各部件预防性维修时里程Table 6 Mileage during preventive maintenance of each component 通过表5和表6可以得出,在二维初始保修期内,动力系统共进行了81次预防性维修活动,预防性维修次数较多,造成了保修成本的浪费和动力系统可用度的降低。同时可以发现,各部件之间存在许多时间相近的预防性维修,因此采用机会维修的方式将其组合起来将极大地减少预防性维修次数,进而降低保修成本,提高动力系统可用度。 步骤1在可行域内随机生成η个初始可行解,这些个体共同构成规模为η的初始种群I0=[ΔR(1),ΔR(2),ΔR(3),…,ΔR(η)]。 步骤2按照第4节的求解算法,计算出每个个体的可用度EA值,可用度越大,则个体的适应度越高。依据适应度对初始种群的个体进行降序排列。 步骤3对初始种群进行选择操作,运用精英保留策略将当前种群适应度最高的3个个体保留至下一代,淘汰最低适应度个体,余下个体依照轮盘赌法进行选择。 步骤4依照设定的交叉概率Pc和变异概率Pm对种群进行交叉和变异操作,产生新一代种群I1,返回步骤2。 步骤5当种群迭代至最大迭代值后终止运算,输出最优解集ΔR。 遗传算法的具体参数设置如表7所示。 表7 遗传算法参数设置Table 7 Parameter setting of genetic algorithm 求解动力系统ΔR的遗传算法的编程步骤如图8 所示。 Genetic Algorithm 1 Begin 2 Parameter setting 3γ=0 4 InitializeIγ=[ΔR(1),ΔR(2),ΔR(3),…,ΔR(η)] 5 While stop critria unsatisfied do 6 forζ=1 toηdo 7 Evaluate fitness ofIγ 8 end for 9 forζ=1 toηdo 10 Select operation toIγ 11 end for 12 forζ=1 toη/2 do 13 Crossover operation toIγ 14 end for 15 forζ=1 toηdo 16 Mutation operation toIγ 17 end for 18 New populationIγ+1 19γ=γ+1;η=length(Iγ+1) 20 end While 21 Output:Best solution ΔRfound 图8 遗传算法编程步骤 在不考虑机会维修的情况下,按照5.1中各单部件的维修计划,可以求得多部件系统的可用度为0.812 3,总期望保修成本为2 685 451元。运用遗传算法求解各单部件机会维修时可靠性阈值,经过270次迭代,以可用度最大为目标求得ΔR=(0.214,0.312,0.246,0.183),此时多部件系统的最大可用度为0.891 7,总期望保修成本为2 435 621元。动力系统可用度随遗传算法迭代情况如图9所示。 图9 遗传算法迭代示意图Fig.9 Schematic diagram of genetic algorithm iteration 运用机会维修策略将动力系统的维修计划进行调整。根据3.3节中多部件系统机会维修策略,动力系统在日历时间维度的维修计划的调整如表8所示。 表8 动力系统机会维修方案Table 8 Opportunistic maintenance scheme of the power system 表8即为该动力系统在日历时间维度调整后的预防性维修计划,调整后,动力系统的预防性维修次数由81次减少到34次。 5.3.1 考虑机会维修与不考虑机会维修对比 机会维修将不同时刻的预防性维修工作组合起来,有效减少了多部件系统的预防性维修次数,进而降低了保修期内多部件系统的预防性维修停机时间,提高了系统可用度。机会维修在减少预防性维修次数的同时,还减少了最小维修次数。这主要是由于由于机会维修依据部件机会维修时可靠性阈值将部件预防性维修的时刻提前,因此有效避免了潜在故障的发生,从而减少了最小维修次数,降低了保修期内的保修成本。考虑机会维修与不考虑机会维修时动力系统保修成本和可用度的对比如图10所示。 图10 考虑机会维修与不考虑机会维修对比Fig.10 Comparison between the situations with and without opportunistic maintenance 根据图10可以看出,不考虑机会维修时,保修期内动力系统的可用度为0.812 3,采用机会维修措施后,保修期内动力系统的可用度提升为0.891 7,提升了10%。不考虑机会维修时,保修期内动力系统的保修成本为2 685 451元,采用机会维修措施后,保修期内动力系统的保修成本减少为2 435 621元,减少了9.3%。通过对比可以看出机会维修策略在提高动力系统可用度、降低保修成本方面效果较好。 5.3.2 考虑故障相关性与不考虑故障相关性对比 不考虑动力系统各部件之间的故障相关性的情况时,也即故障相关系数矩阵χ为零矩阵时,运用与5.2节中同样的求解过程和方法,可以求得此时动力系统的保修成本为2 104 356元,可用度为0.932。考虑故障相关性与不考虑故障相关性的对比如图11 所示。 图11 考虑故障相关性与忽略故障相关性对比Fig.11 Comparison between the situations with and without failure correlation 通过图11可以看出,考虑部件间的故障相关性后,保修成本提高了15.7%,可用度降低了4.3%。显然,忽略多部件之间的故障相关性时,动力系统的保修成本更低、可用度更高,这样的结果似乎更容易被接受。然而部件间的故障相关性是客观存在的,故障独立的假设是不现实的,基于故障独立假设会导致较为严重的分析错误和决策失误,会降低承制单位的保修成本预期,提高部队对系统可用度的预期,在实际的保修实践中,基于该结果制定的保修计划会增加承制单位的成本风险。 5.3.3 一维保修与二维保修对比 二维保修的保修期由两个维度组成,其中一个维度为日历时间,另一个维度为使用强度。本例中多部件系统的保修期为(2 a,2×104km)。一维保修的保修期由一个维度组成,通常为日历时间。当采用一维保修方式时,保修区域由矩形变为上方开口的开放区域,这就造成无论使用率如何变化,保修期均保持为2 a不变,如图12所示。 图12 不同保修方式下的保修区域Fig.12 Warranty area under different warranty methods 图12(a)为二维保修方式下保修区域示意图,图12(b)为一维保修方式下保修区域示意图。不同使用率下,动力系统采用这两种不同保修方式的可用度与保修成本对比如表9所示。依据表9绘制可用度与保修成本随使用率变化趋势图,如图13所示。 表9 不同保修方式下保修成本与可用度对比Table 9 Comparison of warranty cost and availability under different warranty methods 图13 不同保修方式下可用度与保修成本对比示意图Fig.13 Comparison of availability and warranty cost under different warranty methods 由图13可以看出:采用二维保修方式时,随着使用率增加动力系统的可用度先下降、后上升,保修成本则先上升后下降,但整体来看变化不大。这主要是因为实际使用率rl≤rz 本文研究了具有故障相关性的复杂二维保修装备的机会维修策略,针对包含串联多部件系统的复杂装备,在故障相关性分析和单部件预防性维修计划的基础上,以保修期内可用度最高为目标,引入机会维修时可靠性阈值,通过调整各单部件的预防性维修时刻,将各单部件的预防性维修工作进行组合,建立了串联多部件系统二维保修可用度模型,以某新型装甲突击车动力系统为例进行分析。得出以下主要结论: 1)采取机会维修策略后该动力系统的二维保修成本明显降低、系统可用度明显提高,充分验证了机会维修策略的有效性。 2)基于故障独立假设会导致较为严重的分析错误和决策失误,难以为保修方案的制定提供支撑;二维保修方式有助于承制单位节约保修成本并提高系统可用度,随着使用率的增加,二维保修的优势相较于一维保修越来越明显。 3)本文建立的模型可为具有故障相关性的复杂装备二维保修方案制定提供理论和技术支持。考虑到对于部分新型复杂装备而言,部队很难在初始保修期内形成自主维修保障能力,因此下一步需要对具有故障相关性的复杂二维保修装备进行延伸保修决策研究。


4 求解算法


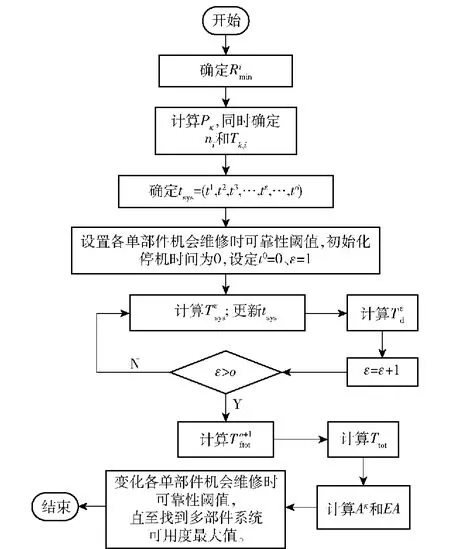
5 算例分析


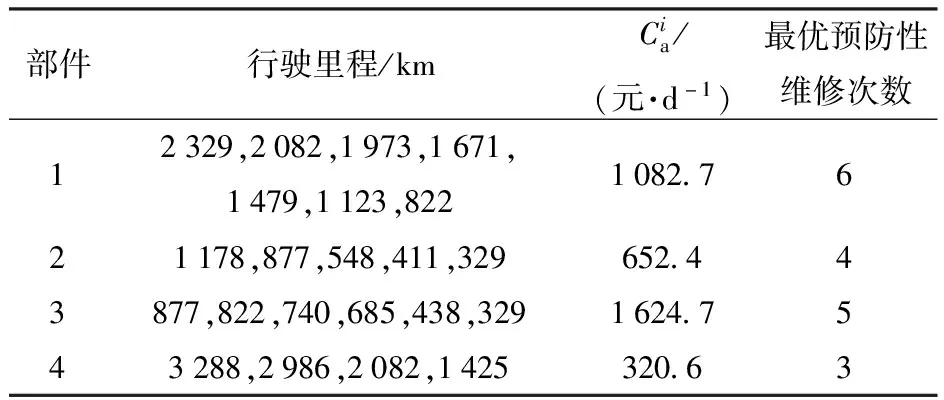
5.1 动力系统单部件维修计划制定




5.2 动力系统机会维修计划制定
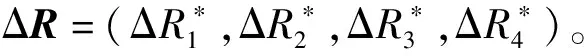

Fig.8 Programming steps of genetic algorithm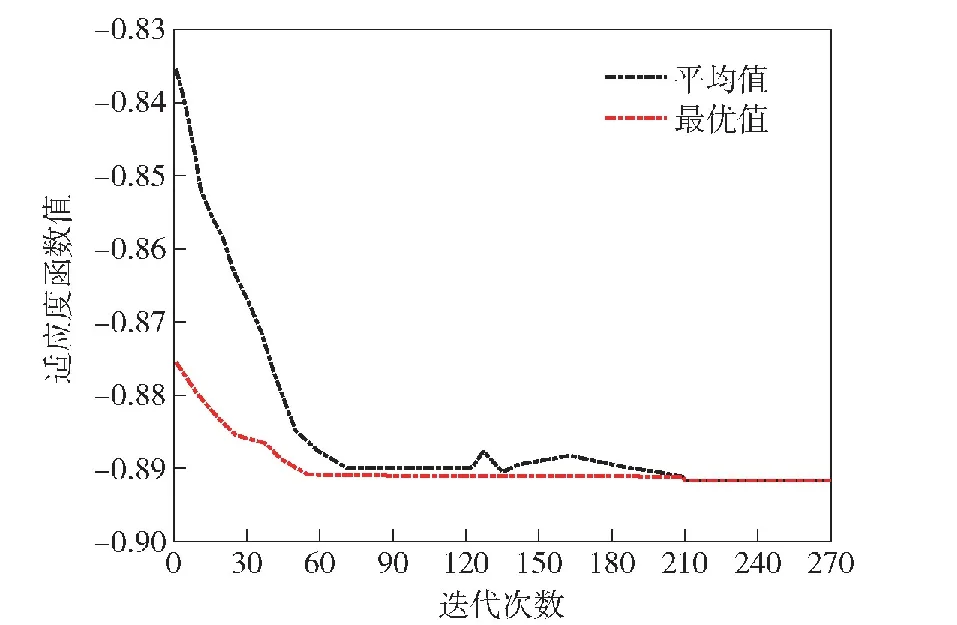
5.3 对比分析
6 结论
