力学等时圆模型

张萍萍

1.模型特征

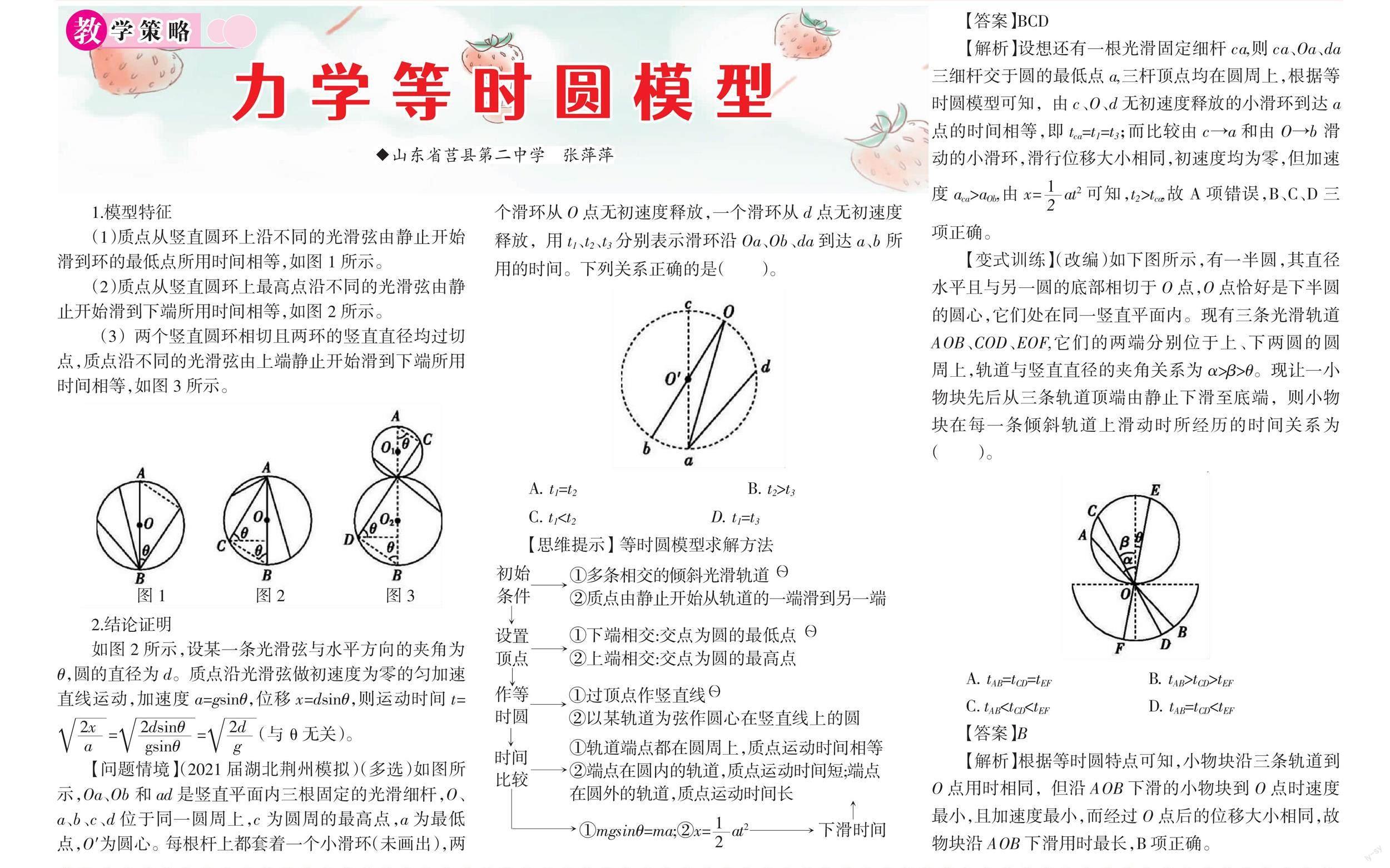
（1）质点从竖直圆环上沿不同的光滑弦由静止开始滑到环的最低点所用时间相等，如图1所示。

（2）质点从竖直圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等，如图2所示。

（3）两个竖直圆环相切且两环的竖直直径均过切点，质点沿不同的光滑弦由上端静止开始滑到下端所用时间相等，如图3所示。

2.结论证明

如图2所示，设某一条光滑弦与水平方向的夹角为 θ，圆的直径为d。质点沿光滑弦做初速度为零的匀加速直线运动，加速度a=gsin θ，位移x=dsin θ，则运动时间 （与 θ无关）。

【问题情境】（2021届湖北荆州模拟）（多选）如图所示，Oa、Ob和ad是竖直平面内三根固定的光滑细杆，O、a、b、c、d位于同一圆周上，c为圆周的最高点，a为最低点，O'為圆心。每根杆上都套着一个小滑环（未画出），两个滑环从O点无初速度释放，一个滑环从d点无初速度释放，用t1、t2、t3分别表示滑环沿Oa、Ob、da到达a、b所用的时间。下列关系正确的是（）。

A.t1=t2B.t2>t3

C.t1

【思维提示】 等时圆模型求解方法

【答案】BCD

【解析】设想还有一根光滑固定细杆ca，则ca、Oa、da三细杆交于圆的最低点a，三杆顶点均在圆周上，根据等时圆模型可知，由c、O、d无初速度释放的小滑环到达a点的时间相等，即tca=t1=t3；而比较由c→a和由O→b滑动的小滑环，滑行位移大小相同，初速度均为零，但加速度aca>aOb，由 可知，t2>tca，故A项错误，B、C、D三项正确。

【变式训练】（改编）如图所示，有一半圆，其直径水平且与另一圆的底部相切于O点，O点恰好是下半圆的圆心，它们处在同一竖直平面内。现有三条光滑轨道AOB、COD、EOF，它们的两端分别位于上、下两圆的圆周上，轨道与竖直直径的夹角关系为α>β>θ。现让一小物块先后从三条轨道顶端由静止下滑至底端，则小物块在每一条倾斜轨道上滑动时所经历的时间关系为（）。

A.tAB=tCD=tEFB.tAB>tCD>tEF

C.tAB

【答案】B

【解析】根据等时圆特点可知，小物块沿三条轨道到O点用时相同，但沿AOB下滑的小物块到O点时速度最小，且加速度最小，而经过O点后的位移大小相同，故物块沿AOB下滑用时最长，B项正确。