航空弧齿锥齿轮低敏感度齿面优化设计

董红涛，任鸿飞，游志伟，薛成

（1.中国航发湖南动力机械研究所，湖南株洲 412002；2.西北工业大学 机电学院，西安 710072）

弧齿锥齿轮作为航空动力推进系统中的重要部件，其接触性能直接影响轮齿的承载能力及传动的可靠性。航空结构的轻量化设计导致齿轮副的支承刚度降低，在高速重载工作过程中，弧齿锥齿轮副的支承会发生变形，导致齿轮副安装距发生偏差，安装距偏差会影响齿面接触印痕的大小与方位，进而影响弧齿锥齿轮的承载能力，为保证航空附件传动弧齿锥齿轮在不同工况下都具有良好的接触性能，开展低敏感度齿面优化设计是十分必要的。

Litvin 等[1-2]应用局部综合等方法，通过预置的传动误差来降低线性传动误差的大小，以提高齿轮传动的耐久性。文献[3-4]确定出计及误差的轮齿接触分析的精确初始点。Ding 等[5]提出一种6σ 健性多目标优化方法，以获得低敏感性的机床加工调整参数。Liu 等[6]通过改进的ICP 算法来精确补偿齿轮偏心和倾斜误差。方宗德等[7]通过设计高重合度传动误差曲线，既提高了弧齿锥齿轮传动的平稳性，又保证了齿轮副的啮合质量，同时降低了齿轮性能对误差的敏感性。Fraňová等[8]通过齿廓修型减小传动误差，以降低齿轮传动系统的振动与噪声。苏进展等[9]通过预设接触迹线沿齿长方向来提高齿轮副的重合度，以改善齿轮副啮合性能。Zhou 等[10]提出一种补偿测量齿面与理论齿面偏差量的一种方法，显著提高了齿轮测量机的精度。刘光磊等[11]提出了一种针对接触印痕位置参数的分析方法，为确定弧齿锥齿轮副安装误差的变动范围提供了参考。唐进元等[12]基于加载接触有限元分析原理，综合分析了误差及变形对弧齿锥齿轮接触特性的影响。彭山东等[13]考虑轴的变形与传动误差数值间的关系，通过改变轴系支撑形式改善传动误差曲线。牟彦铭等[14]通过建立齿面曲率修正模型对预设的高阶传动误差进行优化，以改善齿轮间啮合性能。

以一对航空附件传动弧齿锥齿轮为例，通过分析安装误差的产生过程，对安装误差进行等效处理，基于错位量对接触印痕进行量化，研究印痕与错位量之间的定量关系，基于计及安装误差的齿面接触分析（ELTCA）确定接触印痕对安装误差的敏感度矩阵，建立以灵敏度矩阵绝对值之和为目标函数的稳健性优化模型，采用基于遗传算法的神经网络建立输入输出之间的映射关系，实现弧齿锥齿轮齿面的低敏感度优化设计，也称稳健性。

1 安装误差

1.1 安装误差的产生

本文所研究的安装误差是指在实际工况下弧齿锥齿轮副在啮合过程中，接触区域中心点偏离理论参考点的程度，主要由加工误差、装配误差、热变形、支撑变形等产生，无论从理论上还是从实践中来看，这几部分误差均是不可避免。

1.2 等效安装误差

为了研究安装误差对传动的影响，如图1 所示进行等效[15]。将各错位量正负号方向规定如下：小轮轴向错位量Hp为“−”时移向小端，为“+”时移向大端；大轮轴向错位量Hg移向与小轮相同；轴间距错位量规定齿轮副锥顶重合处为参考位置，从大轮小端向大端看去，小轮在大轮的右边且大轮向上移动时，V为“+”，大轮向下移动时，V为“−”；轴交角错位量Σ为“−”时轴交角减小，为“+”时轴交角增大。

图1 弧齿锥齿轮的错位量

2 齿面印痕的量化

齿面印痕是衡量弧齿锥齿轮啮合质量的关键指标，由于齿面印痕比较直观，使之成为目前对弧齿锥齿轮的设计、制造和检验的主要方法。同时，接触中心的信息也反映在接触印痕中，因此，安装误差对接触印痕的影响，就显得尤为重要。但是，由于接触印痕的形状不规则，要研究安装误差对接触印痕的影响，就必须对印痕进行量化处理。图2 为齿面接触印痕划分模型。

图2 齿面接触印痕划分模型

图3 为接触印痕面积计算示意图，齿面印痕的量化参数分别为：齿面印痕的面积、方向和位置。将所有接触椭圆围成的区域作为印痕的面积，接触迹线的方向作为印痕方向，齿面印痕的中心作为印痕的位置。

图3 接触印痕面积计算

齿面印痕的量化参数具体定义如下：

1）印痕的面积。连接所有接触椭圆长轴的端点，得到近似齿面印痕的多边形，将他们的面积可以近似为齿面印痕的面积，该多边形的面积可以处理为有限个三角形单元的面积之和，设有n个。

根据图4 的接触印痕中心定义，设p1(x1,y1)，p2(x2,y2)，p3(x3,y3)为第i个三角形的3 个顶点及相应坐标，依据文献[16]，可得三角形单元的面积为

图4 接触印痕中心定义

所以印痕多边形面积为

2）印痕的中心。将由接触椭圆组成的多边形按逆时针方向排序p1,p2,···,pn，其坐标为(xi,yi)，i=1，2，...，n，则多边形的中心为：

3）印痕方向。为简化起见，将进入啮合点的接触椭圆中心和退出啮合的接触椭圆中心连线作为印痕方向。用来和齿面2 阶接触参数进行联系。

印痕量化之后，既可以研究齿面印痕与错位量之间的定量关系，进而分析齿面印痕对误差的敏感性；也可用于后续优化加工参数，提高齿轮副啮合稳定性。

3 敏感度分析

在研究弧齿锥齿轮啮合质量关于安装误差的敏感度问题时，是将弧齿锥齿轮安置在已经存在一定安装误差的条件下进行的。理论错位量情况下印痕中心位置、印痕面积和印痕方向为理论印痕参数。错位量在一定范围内变动时，实际得到齿面印痕必将偏离理论齿面印痕。实际印痕参数与理论印痕参数之间的误差，称之为印痕误差。Δx、Δy、ΔS、Δd分别表示理论齿面印痕和实际齿面印痕中心水平位置误差、垂直位置误差、面积误差和方向误差，可表示为：

简记为向量函数

本文灵敏度是基于齿面接触印痕进行的理解，即齿面接触印痕相关量的变化相对于安装误差的变化是否十分灵敏，从而展开稳健度（灵敏度）的定义。基于这样的想法，取弧齿锥齿轮安装误差的初始值为E0，对式（4）进行Taylor 展开，得：

根据式（6）可以看出齿面接触印痕相关量的变化相对于安装误差的变化的灵敏程度，但是由于计算过程复杂，对其进行一定的简化。

依据相关理论研究，采用1阶量进行计算可以保证精度。本文采用本质为向量函数S=(fx,fy,fS,fd)的雅可比（Jacobian）矩阵，用以描述向量函数与其自变量之间的变化关系。故齿面印痕相对于错位量的敏感度定义为：印痕中心位置、印痕面积和印痕方向对4 个错位量的变化率，其几何意义是接触印痕质量对安装错位量的敏感程度，绝对值越大表示对该错位量相对敏感。

齿面接触印痕相对于错位量的灵敏度矩阵S可表示为：

用矩阵形式来表示印痕误差与灵敏度及安装误差之间的关，即

令其他影响因素e1,e2,···,ei−1,ei+1不变，其中的一个影响因子ei在其原值附近发生扰动产生变化，扰动范围一般处于可接受的±10%邻域内。为了保证一定的计算精度，利用中差分公式进行计算，精度较前、后差分公式有所提高。得到4 个印痕误差函数参数对该影响因素的变化率（即1 阶计算量）为

以此来反映影响因素ei对印痕参数的敏感程度。另外，灵敏度Si的数值有正、负之分，正值表示相对于理论印痕参数，印痕质量参数的值是增加，负值表示是减小的。但需要指出的是，轴交角错位量Σ是一个角度微量（单位为rad），与其它3 个错位量（小轮轴向错位量Hp、大轮轴向轮位错位量Hg及中心距错位量V均为长度微量，单位为mm）不同，他们之间属不同量纲不能直接进行比较。这里将轴夹角错位量转换为长度量纲，具体做法为：将轴交角的误差与大轮中点锥距的乘积作为轴交角误差的等效物理量。等效后就可以比较各错位量对印痕参数的敏感程度。

4 低敏感度优化设计

4.1 设计变量

基于局部综合法[17]的弧齿锥齿轮主动设计选取设计变量为2 阶接触参数，即接触迹线与根锥之间的夹角 β、传动比1 阶导数 η及接触椭圆长轴与齿宽比δ。因此，在对弧齿锥齿轮进行低灵敏度设计时，设计变量取x=[x1,x2,x3]T=[β,η,δ]T。

4.2 目标函数

考虑到使用灵敏度矩阵的计算不便性，在此将雅可比矩阵元素绝对值之和作为目标函数来使用，简化计算且保证一定的准确性。

4.3 优化计算模型

根据上述分析，选此为优化计算模型：

式中：β为接触迹线与根锥之间的夹角；η为传动比一阶导数；δ为接触椭圆长轴与齿宽比。

4.4 优化模型求解

考虑到神经网络仅借助实验样本数据，便可建立输入输出间的映射关系，同时使用遗传算法作为神经网络的重要补充，以优化和改善BP 神经网络。本文拟采用基于遗传算法的神经网络[18]对优化模型进行求解。

其中：24 h连续运行设备的日平均耗电量为三鉴/微波探测器日平均耗电量、光口交换机日平均耗电量、网络继电器日平均耗电量三者之和。

由于目标函数是隐函数，不同于其他隐函数的是，其值需通过ELTCA 与差分法计算得出，依据此特性，使用以下的算法：

1）选取n组不同的设计变量值Ei（i=1,2,3,···,n），E=[β,η,δ]，并计算出在Ei处的敏感度Si，作为神经网络训练样本。

2）建立BP 神经网络，并将设计变量作为输入，敏感度作为输出，利用上一步得到的训练样本对其进行训练；此处按照神经网络的默认划分，75%的样本用来训练，15%的用来检验。

3）将神经网络模型作为目标函数，提取公式，为避免初值选取的不便性，利用遗传算法对其进行分析和优化，搜寻在设计范围内的最低敏感度；依据神经网络计算原理，提取训练目标函数，即

4）利用上一步的目标函数值（即利用神经网络计算得到的敏感度的最小值），反求设计变量，经过主动设计步骤，即可设计出满足要求的低灵敏度弧齿锥齿轮副。

稳健性齿面主动设计流程框图如图5 所示。

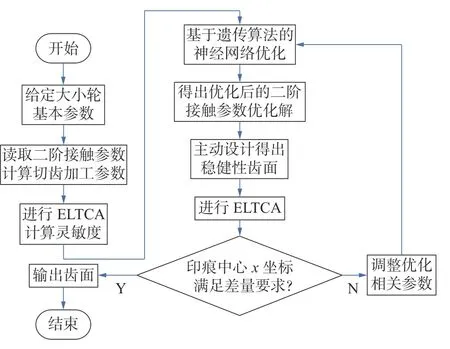
图5 算法流程框图

5 数值算例

以一对航空附件传动弧齿锥齿轮为例，其基本参数如表1 所示，对应的动力与安装误差参数如表2所示。综合考虑重合度以及实际加工中灵敏度的问题，对比不同2 阶接触参数下时的灵敏度矩阵与优化后结果之间的差异：①传统的弧齿锥齿轮设计基于Gleason 齿制，其设计接触路径与根锥垂直，但是同时考虑算法的稳定性，这里将2 阶接触参数置为75°；②高重合度设计的弧齿锥齿轮，重合度系数有所提高，弧齿锥齿轮的接触迹线与根锥夹角较小，这里将2 阶接触参数置为45°；③稳健性优化后的弧齿锥齿轮。3 种工况下的2 阶接触参数如表3所示。

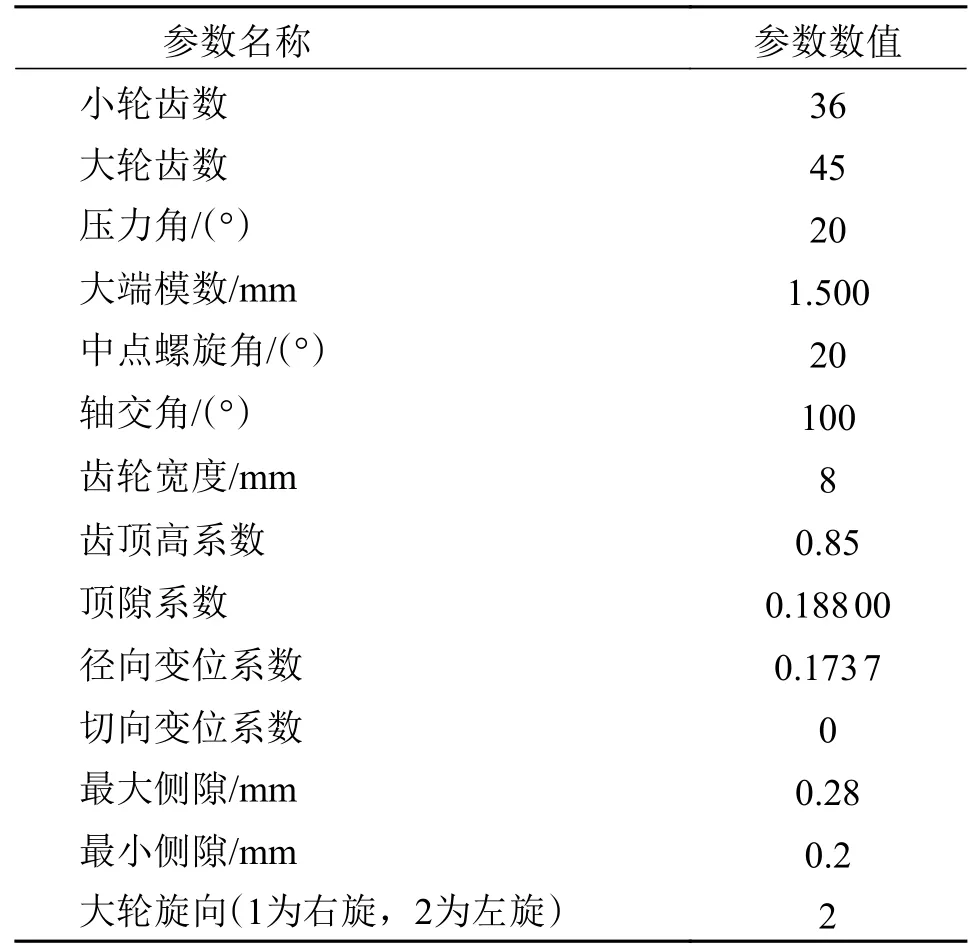
表1 弧齿锥齿轮轮齿基本参数

表2 动力与安装误差参数

表3 优化前后2 阶接触参数

3 种工况下的灵敏度矩阵分别为：

对比S1与S3可以看出，虽然这种设计弧齿锥齿轮的接触迹线与根锥夹角较大，但是其灵敏度确相对较大，即稳健性较低。

对比S2与S3可以看出，虽然高重合度设计弧齿锥齿轮的重合度有所增加，但是同时增大了弧齿锥齿轮齿面接触印痕对于安装误差的灵敏程度。

基于全量误差，计算得出相应优化前后弧齿锥齿轮副的齿面接触印痕以及其相关特性参数，进一步对于接触印痕对于安装误差的灵敏度的对比，图6～ 图8 分别为全量误差3 种工况的接触印痕。

图6 全量误差下75°接触印痕

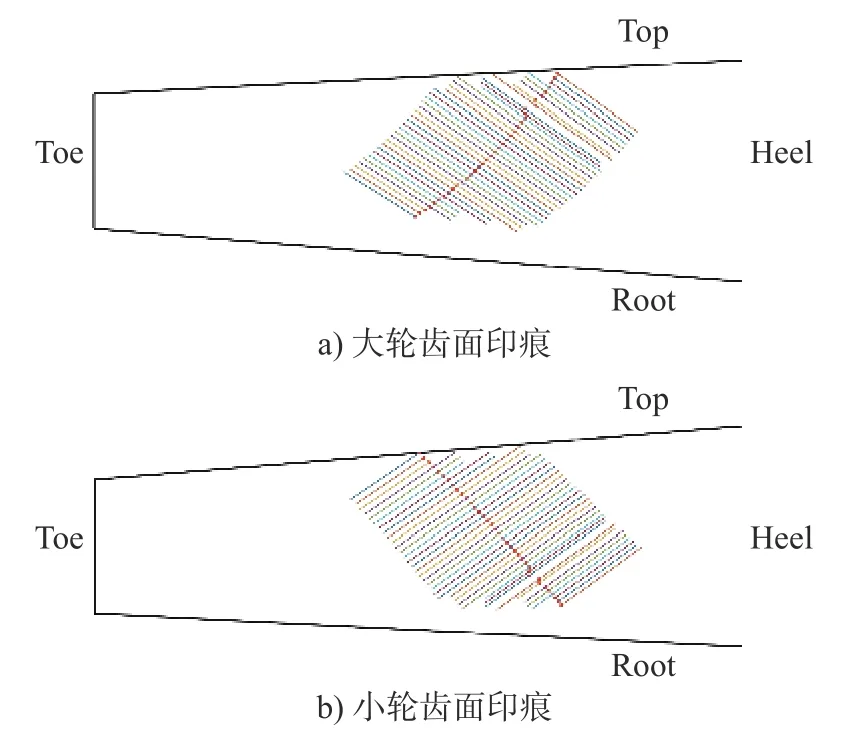
图7 全量误差下45°接触印痕

图8 全量误差下优化后接触印痕

根据接触印痕的定性对比，在全量误差的作用下，两者的齿面接触印痕均比较明显的向齿轮大端移动，明显看出优化前两种参数下加工的弧齿锥齿轮齿面接触印痕对于安装误差较为敏感。同时对于传动会产生不利的影响。对比优化后的结果，在全量误差的作用下，齿面接触印痕没有明显的移动状态，效果较优化前有较大的提升。根据上述对于齿面接触印痕的量化，计算其印痕特征误差量，对比优化前后误差变化情况，如图9～ 图11 所示。

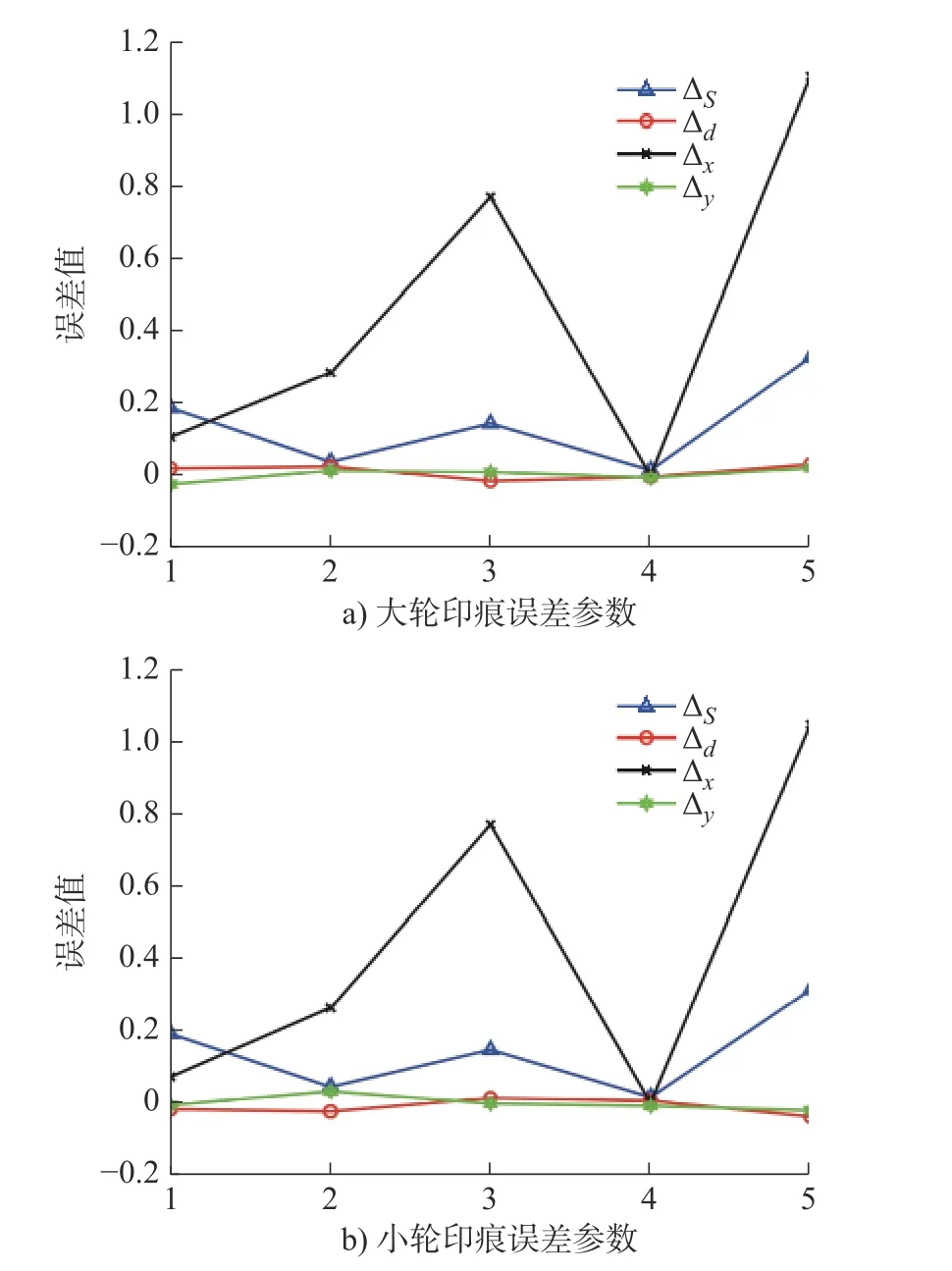
图9 75°下印痕特征参数误差

图10 45°下印痕特征参数误差

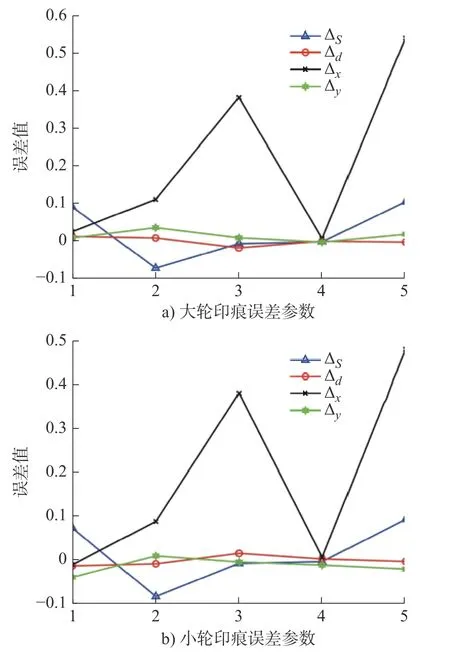
图11 优化后印痕特征参数误差

6 结论

1）对比优化前后印痕特性参数误差的变化，首先可以看出对于同一种安装误差，齿面接触印痕特征参数的变化趋势相同，其中变化量最大的是印痕中心的轴向坐标，其次是印痕的面积，变化最小的是印痕的径向坐标以及印痕迹线方向，这与上述依据敏感度矩阵分析结果一致。

2）第一种2 阶接触参数下的最大变化量为 ∆x=1.143 1 mm；第二种2 阶接触参数下的最大变化量为 ∆x=1.105 4 mm；优化后的二阶接触参数下的最大变化量为 ∆x=0.539 1 mm。定量的可以得出印痕特性参数误差的最大变化量，优化后结果较优化前有52%的降低，优化效果较好，一定程度上提高了传动的平稳性。

3）第一种2 阶接触参数下的次大变化量为 ∆S=0.489 3 mm；第二种2 阶接触参数下的次大变化量为 ∆S=0.327 5 mm；优化后的二阶接触参数下的次大变化量为 ∆S=0.103 4 mm。定量的可以得出印痕特性参数误差的次大变化量，优化后结果较优化前有78.87%的降低，优化效果较好。