基于虚拟水平衡的塔里木河区间水资源优化配置

王露阳

（新疆维吾尔自治区塔里木河流域干流管理局，新疆 库尔勒 841000）

塔里木河流域水资源缺乏，生态环境脆弱[1]，农业灌溉用水所占比重较大，年灌溉用水量达18.91亿m3。为了提高水资源使用效益，需对水资源优化配置进行研究。

1 虚拟水研究对塔里木河流域水资源优化配置的作用

塔里木河干流全长1 321 km，涉及6个县市、7个兵团农场。塔里木河干流多年平均径流量46.5亿m3，2030 年“三条红线”地表水用水总量控制指标10.81亿m3，占径流总量的23.2%，其余水量全部用于生态。虚拟水是用于衡量生产商品的用水量，以作物或产品的用水量来衡量[2]。虚拟水贸易可以改变水的供需结构，粮食贸易蕴含的虚拟水量占地区虚拟水量的绝大部分。所以，通过粮食产量和虚拟水含量，可调控粮食流通和虚拟水流动格局[3]。在塔里木河流域，农业灌溉用水占很大比重，本研究借鉴基尼系数的计算方法，用水资源量和地区国内生产总值分别代表地区水资源和经济发展状况，评估虚拟水流动格局与水资源量分布、地区国内生产总值分布间的均衡性。

1.1 虚拟水流出

虚拟水流出量为：

式中：k=1，2，…，为虚拟水流出区域数量；VWOk为区域k的虚拟水流出量（万m3）；m代表作物类型，为区域k中单位质量作物m的耗水量（万m3/t）；为区域k的出口作物m的质量（t）。

其中：

1.2 虚拟水流入

虚拟水流入量为：

式中：k=1，2…，为虚拟水流入区域数量；VWIk为区域k的虚拟水流入量（万m3）；m代表作物类型；为区域k中单位质量作物m的耗水量（万m3/t）；为区域k的进口作物m的质量（t）。

其中：

式中：为区域k的作物m的需求量（t）；为区域k的作物m的产量（t）。

2 研究方法

2.1 虚拟水平衡的优化框架

选取小麦、玉米作为塔里木河流域主要粮食作物，将各研究分区小麦、玉米种植面积，单位面积灌溉水量，粮食单产的调整幅度作为决策变量，以塔里木河流域GiniVWO最小、GiniVWI最大为调控目标。

2.1.1 资料处理

各研究区域水资源数据来自2016 年新疆水资源公报。各地区国内生产总值、作物种植面积和单产数据来自2017 年新疆统计年鉴。各区域小麦、玉米单位面积灌溉水量来自《新疆维吾尔自治区地方标准农业灌溉用水定额》。各区域小麦需求量按照口粮和种子2 种需求分别推算后汇总，玉米需求量按照口粮、饲料和损耗3 种需求分别推算后汇总。塔里木河流域各地区小麦和玉米需求量、单产、经济收益和灌溉定额详见表1。

2.1.2 基尼（Gini）系数

区域间虚拟水流量是动态变化的，并不稳定，但其应与当地水资源和经济发展状况相适宜。评价两种要素相对分布的均匀程度，可以运用基尼系数的概念[4]。首先，分别计算各地区水资源量占全流域水资源总量比例、各地区国内生产总值占全流域国内生产总值比例、各地区虚拟水输出量占全流域虚拟水输出总量比例以及各地区虚拟水输入量占全部地区虚拟水输入总量比例[5]。然后，按各地区水资源量大小，从低到高进行排序。虚拟水输出格局相对水资源分布的均衡程度（GiniVWO）为：

式中：是地区i虚拟水输出量的累计比例；ri是地区i水资源量的累计比例。另外，按各地区国内生产总值的大小，从低到高排序，进而依次计算各地区国内生产总值和虚拟水输入量的累计比例。据此，虚拟水输入格局相对地区国内生产总值分布的均衡程度（GiniVWI）为：

式中：是地区i虚拟水输入量的累计比例；gi是地区i国内生产总值的累计比例。式（5）和式（6）中，当i=1 时，、ri-1、和gi-1都为0。与基尼系数一样，均衡程度也是一个介于0和1之间的数。其数值越小，说明虚拟水流动格局与水资源分布或地区国内生产总值分布间的均衡性就越高。

2.2 粒子群优化算法（PSO）及其实现

优化算法通常用于解决多目标优化问题，本次水资源管理和配置使用的PSO算法具有无交叉变异计算、参数少、搜索速度快、结构简单等优点。首先初始化一组粒子（随机解），然后通过迭代找到最优解。在每次迭代中，粒子通过跟踪2个极值来更新。决策变量是每个区域主要作物（玉米、小麦）的种植面积。为了比较种植面积不同变异范围的影响，设计了5个方案，每个区域的玉米、小麦种植面积范围分别为0.9～1.1、0.8～1.2、0.7～1.3 和0.6～1.4 倍各自的初始值。利用PSO算法优化区域间虚拟水平衡协调模型的流程，如图1所示。

图1 利用PSO算法优化区域间虚拟水平衡协调模型的流程

3 虚拟水平衡的研究结果分析

3.1 无约束条件下的虚拟水平衡结果

塔里木河流域虽属于干旱少雨地区，但种植的主要作物小麦、玉米除了提供本地区内需外，其余都对外出口，且出口量远大于本地区需求量。因此，研究区域的作物虚拟水输出量都为0，GiniVWI恒为1。上述的多目标模型在GiniVWI恒等于1 的情况下变为单目标模型。

在不添加约束条件下，仅调整作物种植面积，GiniVWO变化最小。本研究选取0.6～1.4、0.7～1.3、0.8～1.2 和0.9～1.1 倍初始种植面积的4 种不同方案。由于方案0.6～1.4 倍的面积调整的模型无法求得最优解，因此仅保留了3 种调整方案。随着调整范围的增大，最小GiniVWI在减小。但此结果是不考虑约束条件存在情况下的。实际上，当作物种植面积减少后，产量势必减少，随着出口量减少，则此区域的经济来源就会下降；当作物种植面积增加后，在原种植条件不变情况下，所需灌溉水量势必会增加，这就给原本水资源短缺的塔里木河地区造成更大的水资源负担。因此，需要考虑相关约束条件对区域最小GiniVWO的影响，并得出效果良好的调整方案。

3.2 不同约束条件下的虚拟水平衡结果

本研究选取种植面积范围在0.8～1.2（0.7～1.3、0.9～1.1 也可）倍初始值情况下添加3 个约束条件，即经济效益、作物供应和灌溉水量。选取经济效益和作物供应0.5、0.6、0.7、0.8 和0.9 倍初始值，灌溉水量1.5、1.4、1.3、1.2 和1.1 倍初始值。每种约束调整都是5种方案，但经济效益的0.9倍初始值和灌溉用水的1.1倍初始值都是模型无解，因此其余方案的结果如图2—4所示。

图2 仅调整经济效益下的minGiniVWO的变化

图2 为仅调整经济效益情况下，随着约束条件范围越来越严格，最小GiniVWO先减小再增大，在0.6倍初始值为最小值。

图3 为仅调整作物供应情况下，随着约束条件越来越严格，最小GiniVWO先增大再减小，到方案4 和方案5 之间减小速率降低。因此，从水资源可持续利用角度考虑，作物供应0.8 倍初始值和0.9 倍初始值取得的模型效果相差不大，但更偏向于考虑方案4。

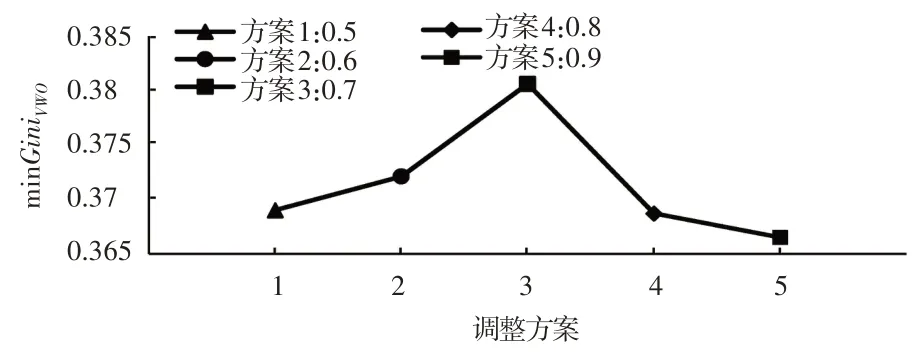
图3 仅调整作物供应下的minGiniVWO的变化

图4 为仅调整灌溉用水情况下，随着约束条件越来越严格，最小GiniVWO先增大再减小。同样方案3和方案4的模型效果差别不大，从减少灌溉用水量考虑，选择灌溉用水1.2倍初始值更加贴合研究目标。

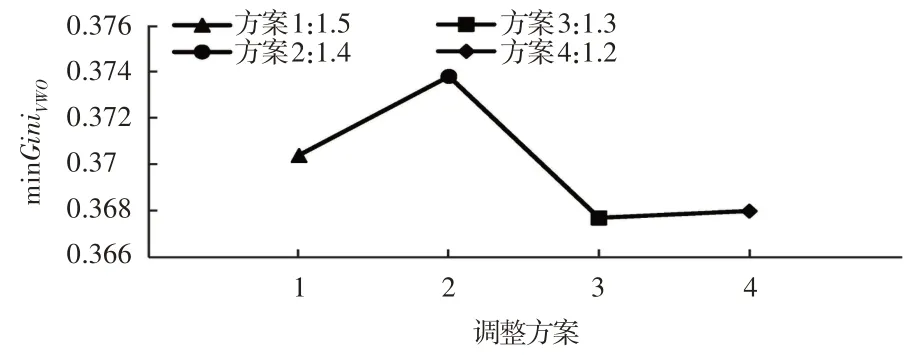
图4 仅调整灌溉用水下的minGiniVWO的变化

综上所述，本研究可以提出一套相对良好的种植方案：经济效益为初始值的0.6倍，作物供应为0.8倍，灌溉用水为1.2倍。其中，经济效益下降较大，但这只是此研究模型所选小麦、玉米2 种作物的经济效益下降。为了减小最小GiniVWO的值，解决干旱地区水资源短缺问题，需要从其他方面来补偿这些下降的经济效益，例如政府补偿、产业转移等等。

4 结语

通过分析探讨，在控制塔里木河粮食种植水消耗量的前提下，以地区虚拟水输出量应与当地水资源量相匹配、虚拟水输入量应与当地经济发展水平相协调为目标，建立了基于虚拟水平衡的区域间水资源优化配置方法体系，可在不同配置策略下促使塔里木河流域水资源得到充分优化，为塔里木河流域未来水资源规划决策和用水公平提供科学依据。